Stringtheorie, M-Theorie, Schleifen-Quantengravitation
| Understanding nature, life, and the universe poses extraordinarily difficult problems ( Lisa Randell, 2011 ) |
String Theory is definitely
Suche ...
Wenn ich mich heute frage, was wohl die drei mich am meisten beeindruckenden intellektuellen Leistungen sind, die einzelne Physiker je vollbracht haben, so fallen mir da vor allem ein:
- Albert Einsteins Allgemeine Relativitätstheorie in ihrer mathematischen Präzisierung,
- Richard Feynmans Einsichten zur Quantenmechanik (vor allem Idee und mathematische Präzisierung des Modells "sum-over-paths") sowie
- Edward Wittens Erkenntnis, dass die 1995 als damals konkurriend angesehenen, hoch komplexen fünf String Theorien nichts anderes sind als verschiedene Sichten
auf ein einziges, wenn auch noch nicht exakt formuliertes universales physikalisches Modell (das er M-Theorie nannte).
Wie Brian Greene berichtet, hat Edward Witten — der Physiker, von dem viele glauben, dass er die Gesamtheit aller Ergebnisse der Stringtheorie am besten überblickt und wohl auch am treffendsten einzuordnen versteht — im März 1998 gesagt: "I feel that we are so close with string theory that — in my moments of greatest optimism — I imagine that any day, the final form of the theory might drop out of the sky and land in someone's lap. But more realistically, I feel that we are now in the process of constructing a much deeper theory than anything we have had before ...".
Wittens Optimismus kam vor allem aus der Tatsache, dass er 1995 alle bis dahin entwickelten, scheinbar zueinander konkurrierenden 10-dimensionalen Varianten der Stringtheorie (immerhin 5) zusammen mit einer damals schon fast wieder verworfenen 11-dimensionalen Supergravitationstheorie als Grenzfälle einer einzigen Theorie nachweisen konnte, die er M-Theorie nannte. Dies genauer untersuchend hat man noch vor 2002 erkannt, dass alle bis dahin betrachteten Varianten der Stringtheorie wunderbar interpoliert werden durch eine einzige, allgemeinere. Susskind sagt uns das so: The language changed a little. We no longer speak of different theories, but rather different solutions of some master theory.
Sie ist erst grob skizziert, aber auf jeden Fall supersymmetrisch.
VORSICHT aber: Selbst die Aussage, dass M-Theorie "erst grob skizziert" sei, wird von Kritikern so nicht akzeptiert. Und in der Tat wies auch Witten selbst noch 2013 darauf hin, dass M-Theorie eher nur Forschungsrichtung denn schon ausgearbeitete Theorie sei. Trotz vieler Details, die man seit 1995 dazugelernt habe, sei das fundamentale Prinzip der M-Theorie weiterhin unbekannt. Man kennt noch kein die M-Theorie definierendes Gleichungssystem (bekannt ist nur ein die Stringfeldtheorie definierendes).
Witten konnte dennoch zeigen, dass die schon bekannten 5 stringtheoretischen Modelle über Dualitäten miteinander verbunden sind. Ferner fiel auf, dass es sich bei Strings in Wahrheit um eine Projektion zweidimensionaler Membranen im Sinne der M-Theory handelt, deren bis dahin übersehene zweite Dimension der zusätzlichen 11-ten Dimension der M-Theorie entspricht. In der Störungstheorie (bei kleiner Kopplung also) war sie zunächst nicht erkannt worden.
In M-Theorie hat man somit statt Strings schlauchartige Branen, und alle Branen der Stringtheorie haben dort ebenfalls eine zusätzliche, kompaktifizierte Dimension. Branen (auch D-Branen genannt) treten auf als die geometrischen Orte, an denen offene Strings enden können. Branen zugeordnet ist Masse oder Ladung (elektrische oder Farbladung).
In der ursprünglichen Stringtheorie mit nur Strings konnte man zwar die grundlegenden Schwingungsmuster der Strings beschreiben, diese konnten aber nicht eindeutig den bekannten Elementarteilchen und Kräften zugeordnet werden.
Erst die Einführung von Branen löste dieses Problem. Die verschiedenen Schwingungsmodi der Branen, sowohl offen als auch geschlossen, können nun Elektronen, Quarks, Photonen, Gluonen und andere Elementarteilchen sowie die Gravitation erklären (s. hier).
Die unterschiedlichen Dimensionen der Branen (0-Branen, 1-Branen = Strings, 2-Branen, 3-Branen) entsprechen dabei unterschiedlichen Arten von Teilchen.
Beweisbar wurde nun auch, dass sich das Modell der M-Theorie auf genau fünf unterschiedlichen Wegen durch Projektion zu einem Modell im Sinne der 10-dimensionalen Stringtheorie machen lässt. Diese fünf Modelle vorher schon gefunden zu haben spricht für die Gründlichkeit der Stringtheoretiker.
Da man noch nicht gelernt hat, mit M-Theorie umzugehen, basieren sämtliche heute bekannten stringtheoretischen Anwendungen immer noch auf einer der 10-dimensionalen Stringtheorien.
Wittens Erkenntnis war rein mathematischer Natur und damals schon vorbereitet durch zwei frühere Entdeckungen anderer Physiker:
- Schon in den 1980-er Jahren war erkannt worden, dass Strings, die sich in 10 Dimensionen – eine davon zeitartig – bewegen, auch als Oberfläche schlauchartiger Gebilde in einem 11-dimensionalen Raum modellierbar sind (man nennt sie heute p-Branen bzw. Membranen).
- Über Jahre hinweg war die Idee der Membranen (kurz: Branen) wenig beachtet worden, bis dann schließlich in den 1990-er Jahren Joe Polchinski herausfand, dass in Theorien, in denen die Strings keine Schleifen bilden, also Enden haben, diese Enden auf Branen verwurzelt sind. Diese Membranen nennt man heute D-Branen. Wie gewöhnliche p-Branen können auch sie auf mehr als nur zwei Dimensionen verallgemeinert sein.
Welch leider erst schemenartige Gestalt selbst M-Theorie heute noch hat, wird klar, wenn man hep-th/9612121 liest. Dass sie immer noch nicht klar definiert ist, wird dort entschuldigt mit der Aussage One excuse for this is that whereas definitions may come first in mathematics they usually come last in physics.
Besonders interessant – bisher aber noch völlig unverstanden – sind der M-Theorie innewohnende "Dualitäten" ganz erstaunlicher Leistungsfähigkeit, deren Ursache man sich bisher aber noch überhaupt nicht erklären kann. Sie erinnern an Automorphismen im Sinne der Mathematik und man kennt mindestens ein Beispiel für ihre Leistungsfähigkeit. Noch unbekannt ist der Typ der algebraischen Struktur hinsichtlich derer sie Morphismen wären. Da Mathematiker keine populärwissenschaftlichen Bücher schreiben, weiß ich nicht, wie weit sie schon sein könnten, diese Struktur dingfest zu machen.
Anders gesagt: Eine wichtige Rolle spielen in der M-Theorie vorhandene Dualitäten (eine Art schwacher "Isomorphie" zwischen je zwei der 10-dimensionalen Stringtheorien). David Gross — der Schöpfer der Heterotischen Stringtheorie — vermutet deswegen, dass es ein grundlegendes, bisher noch nicht erkanntes zentrales Symmetrieprinzip der M-Theorie geben könnte.
Anders als in der Quantenfeldtheorie, treten in den Gleichungen der M-Theorie keine Unendlichkeiten mehr auf. Dieses liegt daran, dass Wechselwirkung — in der QFT noch Wechselwirkung zwischen punktförmig gedachten Teilchen — in der Stringtheorie durch temporäre Verschmelzung, d.h. durch flussartiges Vereinigen und Teilen von Strings zustande kommt (eine geometrisch deutlich genauere Sicht).
Soweit ich (als Mathematiker, aber dennoch als Laie, was Physik betrifft) Brian Greenes Ausführungen verstanden habe, lässt sich die M-Theorie nach Zweck, Wesen und bisherigem Ergebnis beschreiben wie folgt:
- M-Theorie ist eine Menge hoch komplexer, derzeit dieser Komplexität wegen in vieler Hinsicht erst approximativ formulierter Gleichungen, derart dass dieses Gleichungssystem vielleicht sogar unendlich viele Lösungen hat, deren jede als Kandidat für ein umfassendes Modell aller in unserer Welt wirkenden Kräfte in Frage kommen könnte.
- Interessant ist, dass der Kosmos der M-Theorie nach 11 Dimensionen hat: eine davon ist die Zeit, die anderen 10 sind räumlicher Art, wobei einige davon — wenn sie denn wirklich nicht einfach nur konzeptueller Natur sein sollten — extrem stark gekrümmt vorliegen; nur so nämlich ließe sich erklären, dass Experimentalphysik sie bislang (noch?) nicht nachweisen kann.
- Vorsicht aber: M-Theorie erzwingt NICHT, dass die Zahl kompaktifizierter Dimensionen überall im Kosmos gleich groß ist. Unterschiedliche Blasen-Universen im Sinne
der Theorie ewiger Inflation könnten —
auch in Abhängigkeit der dort herrschenden Temperatur — mehr oder weniger kompaktifizierte Dimensionen haben.
Letzlich ist sogar nicht auszuschließen, dass sogar die 3 Raumdimensionen, derer wir uns bewusst sind, aufgerollte sind — aber halt nur solche mit extrem großem Rollradius. Auf jeden Fall legt Stringtheorie uns nahe, dass die mathematische Form der Raumzeit im Sinne Einsteins nur eine relativ grobe Approximation an die wirkliche, in unserer kosmischen Umgebung gegebene sein könnte. - Tatsache ist, dass Stringtheorie nur Sinn macht, wenn man davon ausgeht, dass die Raumzeit entweder 10 oder 26
Dimensionen habe (nur dann nämlich bedarf es keiner Renormierbarkeit).
- Dies erklärt und begründet Michio Kaku, ein Stringtheoretiker, in seinem Buch » Die Physik der unsichtbaren Dimensionen «. Seine Begründung akzeptiert,
scheint mir dann aber nicht so ganz richtig, was
Wikipedia auf Seite » Zur 11-ten Dimension « sagt.
Aber vielleicht spielt hier eine Rolle, dass Dimensionen ja im Grunde nur unabhängig von einander variierbare Freiheitsgrade sind; siehe dazu: Was ist ein N-dimensionaler Raum im Sinne der Physik?
Nebenbei noch: Renormierbarkeit ist ein mathematisch recht fragwürdiges Vorgehen, mit dem man gewisse nicht konvergente Reihen durch konvergente, physikalisch fast so sinnvolle ersetzt, um so noch einen brauchbaren Summenwert zu erhalten. Das funktioniert recht gut in der Feldtheorie der Elektronen und Photonen, funktioniert aber überhaupt nicht mehr beim Versuch, auch Gravitation noch feldtheoretisch zu beschreiben. Grund hierfür: Da Energie Quelle von Gravitation ist, tragen auch die Gravitonen selbst (als Austauschteilchen) zum Gesamtfeld der Gravitation bei. Deswegen muss jedes virtuelle Graviton in der Wolke von Gravitonen um das zentrale, weniger virtuelle Graviton selbst wieder von einer eigenen Wolke weiterer Gravitonen umgeben sein — und so fort bis in alle Unendlichkeit: Wolken um Wolken um Wolken ... jede Summe unendlich vieler Energieportionen. Hier nun kann man sich um das Problem der Unendlichkeiten nicht mehr drücken, sie nicht wegzudiskutieren: Für eine unendliche Kette von Unendlichkeiten gibt es keine Renormierungsmethodik und daher auch keine Hoffnung, aus solcher Feldtheorie brauchbare Prognosen zu gewinnen.
Der Grund, warum man zusätzliche Dimensionen — obgleich bislang nicht nachweisbar — als vorhanden vermutet, liegt darin, dass nur wenn sie existieren, sich einige ansonsten von der Stringtheorie vorhergesagte Singularitäten und auch gewisse Unstimmigkeiten (die Eigenschaften der Naturkräfte betreffend) auflösen: Nur wenn man 10 oder 26 Dimensionen annimmt, wird ein in stringtheoretischen Rechnungen auftretender Term, der viele Unendlichkeiten zur Folge hätte, überall zu Null. Aber natürlich könnte auch die Annahme, dass er zu Recht entfallen muss, eine ähnliche Vereinfachung der Wirklichkeit bedeuten wie Einsteins Annahme, dass es nur 3 Raumdimensionen gäbe.
Note: Im Kapitel Gravity and Large Extra Dimensions (Seite 394-400 seines Buches The Fabric of the Cosmos) beschreibt Brian Greene ein Experiment, mit dem es möglich wäre die Existenz zusätzlicher Dimensionen unseres Universums zu verifizieren — das allerdings nur, wenn es gelänge, zu messen, wie die Gravitationskraft wächst, wenn man zwei Objekte in einer Entfernung aufeinander zubewegt, die kleiner ist als der Durchmesser unseres Universums in eben diesen zusätzlichen Dimensionen (gekrümmte, aufgerollte Struktur dieser Dimensionen hätte endlichen Durchmesser zur Folge). Bislang war 1/10 Millimeter der kleinste Abstand, für den es gelang, dieses Experiment hinreichend genau durchzuführen.
Nebenbei: Schon 1919 hatte ein Zeitgenosse Einsteins — Theodor Kaluza — den Verdacht, dass unser Universum mehr als nur 3 räumliche Dimensionen haben könnte. Er hat Einsteins Gleichungen der Allgemeinen Relativitätstheorie auf 4 Raumdimensionen hin angepasst und gesehen, dass sie dann auch Maxwells Gleichungen, die die elektromagnetische Kraft beschreiben, als Spezialfall mit enthalten. Trotz dieses erstaunlichen Ergebnisses wurde Kaluzas Theorie etwa 1940 aufgegeben, da klar wurde, dass sie Widersprüche enthält zu dem, was die Experimentalphysik bis dahin über Eigenschaften der Elementarteilchen hinzugelernt hatte. M-Theorie vermeidet diese Widersprüche, führt aber zwingend zur Vorhersage von 10 bzw. 11 (statt nur 4) Raumzeit-Dimensionen.
- Anders als klassische physikalische Theorien (Einsteins Relativitätstheorie etwa oder die Quantenmechanik) ist jedes aus der M-Theorie kommende Modell eines Universums so beschaffen, dass es sämtliche Eigenschaften seiner Elementarteilchen eindeutig bestimmt (deren Kenntnis also nicht voraussetzt). Dies ist deswegen von großer Bedeutung, da viel darauf hindeutet, dass es über die bisher durch die Experimentalphysik nachgewiesenen Arten von Elementarteilchen hinaus noch weit mehr gibt — im Prinzip unendlich viele. Der Grund hierfür:
- Als nicht weiter zerlegbare Teile des Universums sieht Stringtheorie schwingende Gebilde, deren jedes
einen p-dimensionalen, in einigen seiner Dimensionen zudem stark gekrümmten Raum darstellt, p jeweils mindestens 1 und
höchstens 6 (oder 7?), wenn man von 6 kompaktifizierten Dimensionen ausgeht [E].
Man nennt diese Gebilde p-branes, im Fall p = 1 auch Strings.
Strings kann man sich vorstellen als Fäden, die- entweder geschlossene Schleifen darstellen (und sich dann überall hin bewegen können)
- oder einer Wäscheleine gleichen, deren Enden festgemacht sind an zwei — nicht notwendig verschiedenen — Branen (d.h. an mehrdimensionale Teilräumen der 11-dimensionalen Raumzeit im Sinne der Stringtheorie).
Note: Branen haben maximal 6 Dimensionen. Das liegt daran, dass Strings und Branen nur in den kompaktifizierten Dimensionen leben, also nicht in den uns bewussten 3 Raumdimensionen. In den meisten Varianten der Stringtheorie ist dieser 6-dimensionale kompakte Teilraum der 10-dimensionalen Raumzeit ein sog. Calabi-Yau-Raum. Inzwischen aber hat sich gezeigt, dass auch noch andere kompaktifizierte 6-dimensionale Räume sinnvolle Lösungen der Stringtheorie darstellen. Sie sind noch kaum untersucht.-
Die Strings — aber nicht die höher-dimensionalen Branen — haben diskrete Schwingungszustände:
Jeder einem String (d.h. einer 1-brane) mögliche Bewegungszustand (Schwingung, eventuell kombiniert mit Rotation) entspricht einem Elementarteilchen bestimmten Typs:
Das Elementarteilchen — als Energieportion — ist eine der Anregungsenergieen des Strings.
Das Spektrum der Anregungsenergien ist gequantelt, wobei die Quantisierungseinheit durch die dem String eigene Fadenspannung bestimmt ist: Je höher die Fadenspannung, desto größer ist die für einen bewegten Zustand des Strings erforderliche Anregungsenergie.
Die erlaubten String-Anregungsenergieen sind ganzzahlige Vielfache einer für den String S charakteristischen Stringenergie E(S).
Es zwei Arten von Strings: solche mit zwei Enden (sog. offene Strings), aber auch in sich geschlossene. Treffen die Enden eines offenen Strings aufeinander, können sie sich verbinden, womit dann ein geschlossener String entsteht. Umgekehrt können geschlossene Strings zerreißen und sich dabei öffnen, d.h. sich in zwei oder mehr kleinere zerlegen.
Diese Prozesse und auch das Wechseln des Strings von einem Bewegungszustand in einen anderen entsprechen der Umwandlung einer Teilchenart in eine andere, wie sie in großen Teilchenbeschleunigern fortwährend zu beobachten ist.
Mehr dazu in Schwingende Strings.
Stringtheorie kennt auch 0-branes. Man muss sie verstehen als Punkte, an denen Strings befestigt sein können. Eine spezielle Ausprägung der Stringtheorie (Matrix Theory) sieht 0-branes als die einzigen unteilbaren Teile — Strings und alle höher-dimensionalen Branes seien daraus aufgebaut.
Das Wort brane, zu deutsch Membran, wurde gewählt in Anlehnung an den 2-dimensionalen Fall. Die Erkenntnis übrigens, daß es die Fälle 1 < p überhaupt gibt, kam erst mit der M-Theorie, d.h. ab 1995 (was erklärt, warum man vorher von "String" Theorien sprach, statt zutreffender von "Membranen" Theorien).
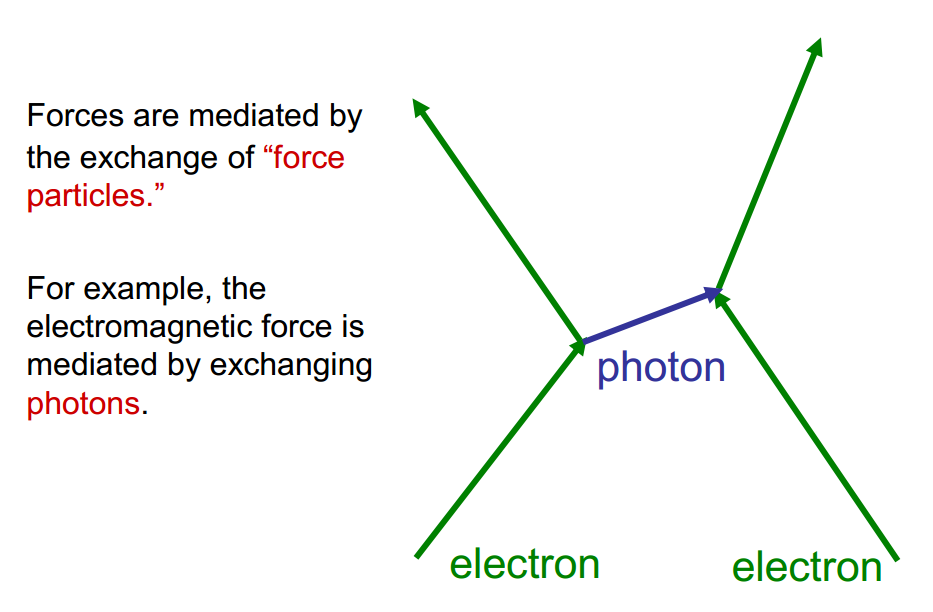
Elementarteilchen im oben erklärten Sinne sind auch die kleinsten in der Natur auftretenden Kraftportionen:- Photon (= unteilbare Portion der elektromagnetischen Kraft),
- Graviton (= unteilbare Portion der Gravitationskraft),
- Gluon (= unteilbare Portion der starken Kernkraft) und
- Bosonen Z, W+ und W- (= unteilbare Portionen der schwachen Kernkraft).
Insbesondere ist Stringtheorie die erste Theorie, die auch die Gravitationskraft als gequantelt vorhersagt: Geschlossene Strings führen zwangsläufig auf ein masseloses Teilchen mit Spin 2 (das Graviton).
Und wie Richard Feynman als erster zeigen konnte, kann jede relativistische Theorie, die einen Austausch masseloser Spin-2-Teilchen enthält, die Feldgleichungen der Allgemeinen Relativitätstheorie reproduzieren.
So also erklärt sich, dass die Stringtheorie auch eine Theorie der Quantengravitation sein kann.
Witten sagt: Erkannt zu haben, dass jede Stringtheorie auch die Schwerkraft berücksichtigt, habe für ihn » die größte intellektuelle Erschütterung meines Lebens « bedeutet.
WICHTIG: Jede unteilbare Portion einer Kraft oder Masse ist nur insofern unteilbar, als sie sich nirgendwo in noch kleinere Portionen gegliedert zeigt. In kleinere Teilchen zerfallen (d.h. in sie umgewandelt werden) kann sie durchaus. Jeder Quanteneffekt ist Neukonfiguration einer Menge von Strings und ihrer Bewegungszustände.
Photon, Graviton und Gluon (nicht aber die W- und Z-Bosonen) sind ohne Masse. Dass letztere aus der Reihe tanzen ist erstaunlich, da die elektromagnetische Kraft und die schwache Wechselwirkung in den 70-er Jahren als unterschiedliche Formen ursprünglich nur einer einzigen Kraft — der sog. elektroschwachen — erkannt wurden [ew].
Wie man vermutet, waren unmittelbar nach dem Urknall — bzw. vereinigen sich bei sehr hoher Temperatur — sogar alle vier Grundkräfte zu nur einer einzigen [u].
Anzahl und Eigenschaften der in irgend einer kosmischen Umgebung existieren Elementarteilchen sind — so sagt die Stringtheorie — abhängig von der Geometrie des Raumes und der Form der Kompaktifizierung seiner Dimensionen.
Der Astrophysiker Paul Davies schreibt daher: Die Kosmologie ist zu einer Umweltwissenschaft geworden, in der ein wesentlicher Teil der Erklärung dessen, was wir in unserem Universum beobachten, auf den Eigenschaften unserer lokalen kosmischen Umgebung beruht. Wo eine Region im Kosmos sich aus einem extrem kompakten Zustand heraus urknallartig befreit und dabei schnell abkühlt, ist natürlich zu erwarten, dass sie der damit verbundenen vielen Symmetriebrüche wegen recht individuelle Eigenschaften bekommt — bis hin zu eigenen Werten für die Größen, die man begrenzter Beobachtungsgenauigkeit wenigstens lokal als Naturkonstanten einstufen darf.
Lokal in diesem Sinne bedeutet: Innerhalb der Beobachtungshorizonte von Objekten, die noch Einfluss aufeinander haben können.
- Interessant auch: Die Stringtheorie, so behaupten einige Stringtheoretiker, zeige eine überaus enge Verwandtschaft zwischen Elementarteilchen und Schwarzen Löchern.
Ebenso wie jedes Elementarteilchen sei nämlich auch jedes Schwarze Loch Schwingungszustand eines Strings.
So schreibt z.B. Susskind, der mit als einer der Väter der Stringtheorie gilt, in 2013:
One of the deepest lessons we have learned over the past decade is that there is no fundamental difference between elementary particles and black holes. As repeatedly emphasized by 't Hooft [A], [B], [C], black holes are the natural extension of the elementary particle spectrum. This is especially clear in string theory where black holes are simply highly excited string states. Does that mean that we should count every particle as a black hole?
Leider ist dies wieder ein Beispiel dafür, dass bei Stringtheoretikern oft der Wunsch der Vater des Gedankens zu sein scheint. Smolin nämlich relativiert Susskinds Aussage ganz gewaltig, indem er ihm antwortet:
The only results in string theorie that describe black holes in any detail describe only very atypical black holes. In those cases, they are related – at least by indirect argument – to states described by string theory, but they are not in fact excitations of strings. They involve instead objects called D-branes. So Susskind must mean by "a highly excited string state" any state of string theory. But in this case the argument has no force, as stars, planets, and people must also be "highly excited string states".
Quelle: John Brockmann (ed.): The Universe (2013), p. 179 (Susskind) and p. 209 (Smolin).
Eine Vorhersage der Stringtheorie soll auch sein, dass alle elementaren Materieteilchen Schwarze Löcher sind (sog. extreme Schwarze Löcher).
Quelle: Timothy Ferris: Chaos und Notwendigkeit (1997), S. 274
- Typische Größe der Strings, Membranen oder p-branes scheint 10-33 cm zu sein (die sog. Planck-Länge).
Da die Stringtheorie selbst jene Größe aber nicht erzwingt, kann nicht ausgeschlossen werden, dass selbst die kleinsten Strings um viele Größenordnungen länger sind
oder dass einzelne Strings (bzw. Membranen) beliebig groß sein könnten — im Extremfall sogar so groß, dass Astronomen sie zu entdecken in der Lage wären.
Genau genommen aber sind Strings und Branen schwingende Kraftfelder. - Ihre Masse bzw. Energie ist nur im Ausnahmefall klein, ansonsten aber weit größer als die der Protonen und auf jeden Fall
proportional sowohl zur Frequenz, in der sie schwingen, als auch zur Spannung, unter der sie stehen.
Die meisten p-branes sind so energiereich (= massereich), dass es den Experimentalphysikern wohl für immer unmöglich sein wird, sie gezielt ins Leben zu rufen (entsprechend große Teilchenbeschleuniger zu bauen ist unmöglich). Sollte man sie — die ja mit zunehmender Masse auch zunehmend instabil sind — als Rest kosmischer Katastrophen oder gar des Urknalls dennoch mal entdecken, wäre das eine richtige Sensation. - Für die am wenigstens gespannten p-branes errechnet sich eine Spannung von etwa 1019 Tonnen.
- Die mit etwa 1039 Tonnen am stärksten gespannten stellen das sog. Graviton dar, die kleinste Portion also, in der die Gravitationskraft auftreten kann. Wo immer sie auftritt, ist ihre Stärke ganzzahliges Vielfaches eben dieser Portion.
- Nun noch zum Begriff der Dimension, da der ja nun in der Physik eine weit größere Rolle spielt als noch vor 1995:
Als Mathematiker hat man keinerlei Schwierigkeiten, sich Räume vorzustellen, die mehr als 3 Dimensionen haben (oder gar unendlich viele). Für Nicht-Mathematiker aber sei gesagt, dass die Aussage, ein Raum habe p Dimensionen, einfach nur bedeutet, dass jeder Punkt in diesem Raum seiner Lage nach beschreibbar ist durch durch p Zahlen, die — und genau das macht den Dimensionsbegriff aus — ohne jede Abhängigkeit von einander variierbar sind (so daß wirklich jede Kombination solcher Zahlen eine im Raum tatsächlich existierende Position darstellt; welche genau hängt vom gewählten Koordinantensystem ab).
Beispiel für einen Raum, der eine endliche und eine nicht endliche Dimension hat, ist z.B. die Oberfläche eines unendlich langen, überall gleich starken Seiles. Wer es aus großer Entfernung betrachtet, wird es als eindimensional sehen (als Faden also, dessen Dicke man nicht mehr als zusätzliche Dimension wahrnimmt).
Dieses Beispiel zeigt, wie es kommt, dass sich tatsächlich existierende Dimensionen in der Tat verstecken können. - Die M-Theorie scheint nicht auszuschließen, dass Universen auch ineinander geschachtelt auftreten könnten (gewisse Membranen dann also Teil gleich mehrerer Universen sind). Ob die dann zwingend identische Physik haben müssen oder ob das kleinere, im größeren enthaltene Universum dann dort nur als Membran erscheint, wird in Greenes Buch nicht diskutiert.
- Brian Greene spricht z.B. über die Möglichkeit, dass Schwarze Löcher einfach nur Membranen sein könnten: gigantisch schwere Elementarteilchen also, die komplett beschrieben sind durch Zahlen, die Masse, Kraftladungen und Spin beschreiben. [Dass Schwarzen Löchern und Elementarteilchen gemeinsam ist, durch diese sechs Eigenschaften komplett beschrieben zu sein, ist Physikern schon lange bekannt und hat sie stets gewundert.]
- Der Vollständigkeit wegen sei erwähnt, dass es eine Variante der M-Theory gibt, die mindestens zwei Dimensionen mehr erlaubt: die sog. F-Theory.
Damit scheint, was die Zahl der Dimensionen unseres Universums betrifft, das letzte Wort noch nicht gesprochen.
In diesem Zusammenhang sei betont: Sind p1 und p2 zwei Dimensionen mit 1 <= p1 < p2 und ist
o1 ein in ein p2-dimensionales physikalisches Objekt o2 eingebettetes p1-dimensionales Objekt, so läßt sich o1 seinem Wesen nach komplett verstehen ohne seine Einbettung nach o2 zu betrachten (oder auch nur von ihr wissen zu müssen). Relevant wird solche Umgebung erst dann, wenn man mögliche Interaktionen von o1 mit anderen, höher dimensionalen Objekten (wie etwa o2) zu studieren wünscht.
Konsequenz daraus ist, dass wir nie sicher sein werden, ob der Kosmos nicht doch mehr Dimensionen hat, als wir jeweils kennen — es könnten sogar unendlich viele sein. Da selbst das die Mathematik nicht an die Grenzen ihrer Leistungsfähigkeit bringen würde, könnte man fast auf den Gedanken kommen, die Mathematik selbst sei die gesuchte Weltformel, jenes Gesetz also, das als einziges alle kosmischen Eigenschaften zwingt, so zu sein, wie sie sind. Für diesen Gedanken spricht, daß alle mathematischen Gesetzmäßigkeiten existieren ganz unabhängig davon, ob der Mensch sie kennt oder nicht — sie sind Teil der Schöpfung.
Der einfachste gekrümmte Raum, den ich mir vorstellen kann, ist der 1-dimensionale Raum, der — als Punktemenge — einen Kreis in einer 2-dimensionalen Ebene darstellt. Als "Basisvektor" in diesem Raum kann jeder Kreisbogen dienen, z.B. einer, der genau den halben Kreis H darstellt. Man erkennt dann aber sofort, dass hier jeder Punkt im Raum nur noch dann ein eindeutig bestimmtes Vielfaches dieses "Basisvektors" ist, wenn man die Skalare nicht als reelle Zahlen auffasst, sondern als Element der additiven Restgruppe R mod 2 (R die additive Gruppe der reellen Zahlen). Die Tatsache, dass sie keinen Körper darstellt, und auch nicht ersetzbar ist durch einen endlichen Körper im Sinne der algebraischen Zahlentheorie, lässt mich vermuten, dass der Dimensionsbegriff der Riemannschen Geometrie noch komplizierter sein muss als durch meine Erklärungen oben suggeriert. Zu erklären, wie er sich für die so unregelmäßig gekrümmten Calabi-Yau-Räume dann also wirklich genau charakterisiert, reicht mein mathematisches Wissen nicht aus.
Brian Greene spricht zwar immer wieder davon, dass die üblichen 4 Raumzeit-Dimensionen (x,y,z,t) auch Dimensionen der die p-branes darstellenden Räume sein können, will aber nicht ausschließen, dass auch sie leicht gekrümmt sein könnten, die Dimension unseres Universums dann also endlich wäre.
Tatsache aber ist, dass der Durchmesser der Projektion unseres Universums auf seinen uns so vertrauten 3- bzw. 4-dimensionalen Teilraum extrem viel größer ist als der Durchmesser seiner Projektion auf die anderen 7 Dimensionen. Die nämlich — nennen wir sie P7 — hat nur einen Durchmesser von etwa 10-33 cm (sog. Planck-Länge, typische Größe der p-branes).
Wer sich das durch ein Bild illustriert vorstellt, wird unser Universum dann dort als extrem dünnen, langen Faden erkennen (eine ganz neue Rechtfertigung für die Bezeichnung "String" Theorie). Die Tatsache, dass es sich derzeit ausdehnt, könnte Anzeichen sein, dass es schwingt, und daher — das ist jetzt aber reine Spekulation — selbst String-Charakteristik haben könnte.
[Schade, dass Isaac Asimov nicht mehr lebt: Er würde jetzt wahrscheinlich darüber zu spekulieren beginnen, ob nicht auch umgekehrt jeder p-brane unseres Universums, statt atomar zu sein, selbst wieder komplexes Universum ist, was wir uns vielleicht nur deswegen nicht vorstellen können, weil die durch Heisenberg entdeckte Unschärferelation der Experimentalphysik eine Grenze setzt, die bewirkt, dass physikalische Strukturen sich ganz grundsätzlich nur bis hin zu einer gewissen Genauigkeit beobachten lassen (da der jeweilige Zustand derjenigen ihrer Teile, die sich über höchstens eine Planck-Länge hin erstrecken, mit gewisser Unschärfe behaftet ist). Interessant ist, dass die Stringtheorie — als eine rein mathematische Theorie — aber durchaus in der Lage sein könnte, selbst die jenseits dieser Grenze liegende Welt des Allerkleinsten noch korrekt mit zu beschreiben — immer vorausgesetzt, dass dort wohldefinierte Struktur auch wirklich noch existieren sollte. Genauer:]
Die oben definierten Teilräume P7 modellieren, was die Physiker als Quantenschaum bezeichnen. Die Krümmung des Raumes wird dort — so sagt die Stringtheorie — umso bizarrer, je genauer man hinsieht (sprich: je stärker die "Lupe" ist, unter der man sie betrachtet).
Diese feinste Struktur des Universums korrekt zu beschreiben, ist die Allgemeine Relativitätstheorie viel zu ungenau. Die Quantenmechanik macht hier weit besser zutreffende Vorhersagen, bedient sich hierzu aber einer Methodik, in deren Zentrum Wahrscheinlichkeitswellen stehen und ein Summationsbegriff (Feynmans sum over paths), den wirklich zu begründen bisher nicht gelang. Man sieht nur, dass sich über ihn Vorhersagen ergeben, die durchaus zutreffend erscheinen, obgleich das letzlich bedeutet, dass ein Teilchen, um von A nach B zu kommen, hierfür jeden nur denkbaren Weg durchs Universum nimmt und das entweder zeitlich parallel oder mit unterschiedlicher positiver Wahrscheinlichkeit (!).
Ein Naturgesetz scheint zu sein: Je feiner die Details der Raumstruktur sind, die man betrachtet, desto schneller verändern sie sich der Zeitachse entlang.
[Es ist da also wie auch im Makrokosmos: Wer z.B. die Erde – einen ganzen Planeten also – aus weiter Entfernung betrachtet, wird sie zunächst nur als Punkt wahrnehmen oder als Kugel sehen, als ein sehr einfach geformtes Objekt also. Bei genauerem Hinsehen aber wird man hohe Berge und tiefe Täler wahrnehmen, deren Form sich über lange Zeit hinweg durchaus dramatisch verändert (sie entstehen und vergehen). Beobachter schließlich, die in der Lage wären, aus großer Entfernung selbst noch so kleine Formen wie die von Bäumen, Gebüsch oder Gräsern auf einer Wiese zu unterscheiden, kämen zum Schluss, dass die Oberfläche der Erde grob gesehen sehr einfache, im Detail aber doch extrem bizarre Form hat und dass gerade die kleinsten dieser Formen sich über die Zeit hinweg am schnellsten verändern.
Gerade solcher Parallelität wegen – was Vielfalt und zeitliche Wandlungsfähigkeit von Struktur im Makrokosmos und Struktur im Allerkleinsten betrifft – ist es interessant, dass der M-Theorie entsprechend die Struktur des Quantenschaums einer Dualitätsregel gehorcht, die durch nichts suggeriert wird, was Experimentalphysik bisher zu entdecken in der Lage war:]
P7 – den Quantenschaum also – könnte man vergleichen mit einem sich ständig im Umbau befindlichen Labyrinth, welches zugleich Spiegelkabinett ist. Man hat nämlich entdeckt, dass Calabi-Yau-Räume stets in Paaren auftreten, derart dass
- beide Räume exakt identische Physik bedeuten,
- einer von beiden aber stets deutlich einfachere mathematische Struktur hat als sein Bruder.
Leider sagt Greene uns nicht, ob der gravierende Unterschied in der Komplexität solch dualer Erkenntniswege sich äußert
- als Unterschied in der Komplexität zu betrachtender Formeln,
- als Unterschied in der Kondition der zueinander dualen Rechenprobleme
- oder gar in beider Hinsicht.
Wie verwickelt und unübersichtlich — im Vergleich zur recht einfach gekrümmten Oberfläche z.B. einer Kugel — Calabi Yau Spaces sein können, suggeriert [1] oder z.B. auch die folgende Darstellung einer 3-dimensionalen Schnittfläche durch einen 6-dimensionalen Calabi-Yau-Raum (zweidimensionale Darstellung der 3-dimensionalen Menge aller Punkte des Raumes, die bleiben, wenn man 3 der insgesamt 6 Koordinaten fest vorgibt):
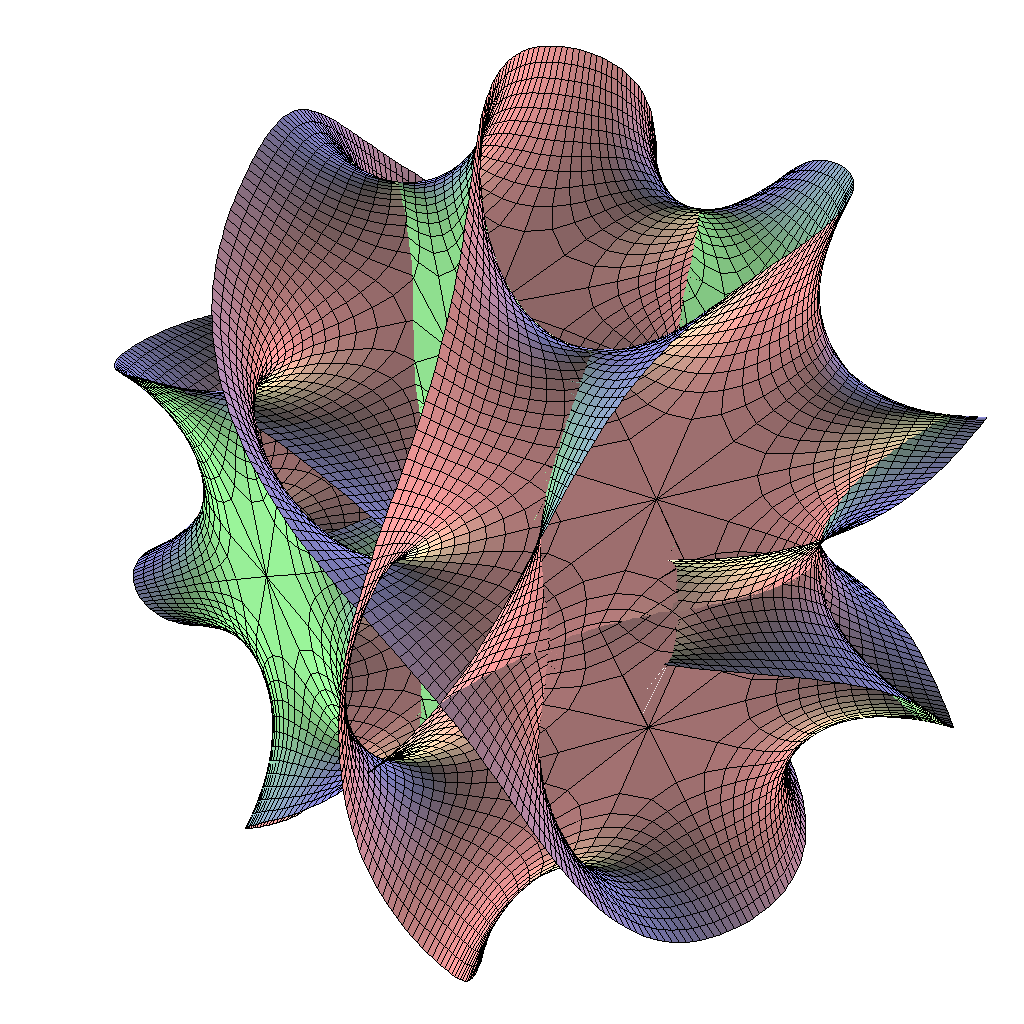
Quelle: Wikipedia
Die 10-dimensionale Raumzeit der Superstringtheorie ist kartesisches Produkt des 4-dimensionalen Raumes im Sinne Einsteins und eines 6-dimensionalen kompakten Raumes, für den — wie man zunächst dachte — nur 6-dimensionale Calabi-Yau-Räume in Frage kämen. Heute weiß man, dass auch noch etwas allgemeinere kompakte Räume sinnvolle Lösungen liefern (so schreibt der Stringtheoretiker Dieter Lüst in: Quantenfische (2014), S. 277).
Nebenbei: Dieter Lüsts Erklärung der Stringtheorie ist für Laien gut verständlich und informativer als alles, was mir sonst an umgangssprachlicher Berschreibung der Stringtheorie begegnet ist. Sein Buch zu lesen — insbesondere ab Seite 225 — kann ich deswegen nur wärmstens empfehlen. Für angehende Studenten der Physik sollte man es als Pflichtlektüre einstufen.
Wie man sich die den Punkten der 4-dimensionalen Raumzeit "angehefteten" kompakten 6-dimensionalen Strukturen vorzustellen hat, erklärt meine Antwort auf Gutefrage.net.
Zur Frage nach der Geschichte unseres Universums haben Hawking und Hertog eine interessante These aufgestellt: Sum over Histories überträgt Feynmans sum-over-paths Idee — die ja längst als durch Experimente bestätigt gilt — in die Zeitdimension. Das erscheint logisch, denn rein mathematisch gesehen sind alle Dimensionen eines Raumes völlig gleichberechtigt.
Zum Schluß sei noch hervorgehoben: Was die String/M-Theorie auszeichnet — und was begündet, warum führende Physiker glauben, damit der gesuchten Weltformel schon sehr nahe zu sein — ist die Tatsache, dass das durch sie gegebene physikalische Modell keinerlei Konstanten mehr enthält, mit der sich das Modell "zurechtbiegen" ließe, wo seine Vorhersagen nicht so ganz tatsächlich beobachteten physikalischen Gegebenheiten entsprechen. Selbst die Größe der Naturkonstanten jedes Universums ergibt sich zwingend aus dem Modell selbst. Brian Greene drückt das so aus: Unlike more conventional theories such as the Standard Model, which has 19 free parameters that can be adjusted to ensure agreement with experimental measurements, string theory has no adjustable parameters.
Was die Physiker das Standardmodell nennen (siehe [1] und [2]) ist eine erst nach 1930 entstandene, enorm erfolgreiche Theorie zur Beschreibung der elektromagnetischen Kraft sowie der starken und der schwachen Kernkraft einschließlich der Wirkung dieser Kräfte auf Materie, die man sich dort in gewisse Elementarteilchen zerlegt denkt. Größte Schwäche dieser Theorie ist, dass völlig offen bleibt, ob es über die darin diskutierten Elementarteilchen hinaus noch weitere gibt (und ob sie sich nicht vielleicht doch auf etwas zurückführen lassen, was noch elementarer ist: Der Zoo aller durch die Experimentalphysik schon nachgewiesener Elementarteilchen ist nämlich schon verdächtig groß).
M-Theory ist gedacht, alle drei Theorien zu ersetzen:
das Standardmodell
und auch die Quantenmechanik.
Nebenbei: Das Standardmodell (der Elementarteilchenphysik) sollte nicht verwechselt werden mit dem kosmologischen Standardmodell, das die Geschichte unseres Universums zum Gegenstand hat: die Geschichte seiner Vergangenheit ebenso wie die seiner Zukunft.
Inflationäre Kosmologie — ein Teil dieses zweiten Standardmodells — legt nahe, dass das gesamte uns sichtbare Universum durch extreme Vergrößerung eines winzigen Volumens entstanden sei und all seine Struktur deshalb extreme Vergrößerungen von Quantenfluktuation im frühen Universum sein könnte.
Hier, so scheint mir, ergibt sich ein Zusammenhang mit dem, was Stringtheorie als möglich erachtet: dass nämlich auch ein ganzes Universum — ebenso wie z.B. ein Schwarzes Loch — letztlich nicht anderes sein könnte als eine extrem große Membran. Umgekehrt könnte man dann aber auch nicht mehr ausschließen, dass — was Mathematik ohnehin nahelegt — auch extrem kleine Membranen noch unglaublich komplexe, ja sogar unendlich komplexe Struktur haben könnten.
Wie sich diese Möglichkeit dann aber mit Heisenbergs Unschärferelation vertragen könnte, ist mir nicht klar (denn die ist ja nicht einfach Beobachtungsgrenze sondern Ausdruck der Tatsache, dass physikalische Strukturen — oder nur ihre Zustände? — quantenmechanischer Effekte wegen nur mit gewisser Unschärfe existieren oder sich nur mit gewisser Wahrscheinlichkeit in den einen oder anderen Zustand begeben. Recht Erstaunliches zur Gesetzmäßigkeit solcher Unschärfe haben 2010 Wehner und Oppenheim aufgedeckt: siehe [P] und Beispiel [B]).
Mindestens dann, wenn die versteckten, kampaktifizierten Dimensionen des Raumes Durchmesser in der Größenordnung der Plancklänge und darunter haben, könnte das überall gegebene Quantenzittern zur Folge haben, dass die Raumzeit sich auf Quantenebene darstellt als eine blubbernde Suppe von Geometrien, die sich ständig abwechseln, so dass die Raumzeit sich zu keiner wirklich entscheiden kann. Dies würde dann aber wohl auch eine entsprechende Unbestimmheit der Naturgesetze bedeuten.
Wie Stringtheoretiker glauben erkannt zu haben, liefert die M-Theorie grob etwa 10500 Modelle für möglicherweise existierende Universen [was man wohl so zu verstehen hat, dass man sämtliche Kompaktifizierungen der versteckten Dimensionen als nur eine zählt, die sich – gerundet hin zur Planckskala – im Bereich unseres Universums, einer ja nur endlich großen Teilregion des gesamten, möglicherweise unendlich weiten Weltalls, nicht mehr unterscheiden].
Die Aufgabe, in dieser dann immer noch unglaublich großen Menge von Modellen jenes zu finden, welches unser Heimat-Universum am genauesten beschreibt, erscheint allzu schwierig. Erste Schritte sie zu lösen, sind dennoch schon unternommen. Hier ein Beispiel:
Das Standardmodell der Elementarteilchenphysik gruppiert schon beobachtete Elementarteilchen nach 3 Familien. Andererseits haben durch p-Branes dargestellte Elementarteilchen unterschiedliche Eigenschaften je nachdem welches Modell (der so überaus vielen) man zugrundelegt. Wirklich zu unserem Universum passen können also nur Modelle, die für die Elementarteilchen Eigenschaften postulieren, die denen entsprechen, die unsere Experimentalphysik bislang beobachtet hat. Eine dieser Eigenschaften entspricht der Gruppierung nach Familien, und etwas dazu Vergleichbares findet sich auch in den durch die M-Theorie erlaubten Weltmodellen: Die Form nämlich, die jedes solche Modell den im Quantenschaum P7 auftretenden Flächen zuordnet, bestimmt wesentlich die Eigenschaften der nach dem jeweiligen Modell möglichen Elementarteilchen.
Edward Witten sieht deswegen als mögliche Kandidaten für das Modell unseres Universums vor allem jene Modelle der M-Theorie, in denen (den 3 real beobachteten Familien von Elementarteilchen entsprechend) die Calabi-Yau-Mannigfaltigkeiten 3 lochartige Trichter aufweisen: Jene nämlich führen zu einer Familienbildung der vom Modell vorhergesagten Elementarteilchen, die der entspricht, die wir vom Standardmodell her kennen.
Nun: Selbst wenn man wirklich sehr gut passende Modelle findet, bedeutet das noch lange nicht, dass M-Theorie nicht Millarden weiterer kennt, die noch wesentlich besser passen.
dass im überzeugendsten jener ihrer Modelle, die der Mensch schon betrachtet hat, Widersprüche zur Realität seines Universums gefunden werden.
Hierdurch, so denke ich, wird es Physikern, die der M-Theorie ablehnend gegenüberstehen, fast unmöglich werden, sich durchzusetzen.
Umgekehrt wird ebenso klar, dass der Weg hin zur Kenntnis der ersehnten Weltformel wohl auch mit Hilfe der M-Theorie von Menschen niemals wird zu Ende gegangen werden können. Neue Erkenntnisse schneller als bisher zu gewinnen wird sie uns aber sicher helfen.
Es gibt Varianten der Stringtheorie, in denen Strings auch negative Energie haben können, womit sie dann Tachyonen wären – Teilchen also, die sich schneller als das Licht bewegen könnten. Da Physiker nicht an Tachyonen glauben, sehen sie diese Varianten der Stringtheorie als nicht sinnvoll an. Tatsächlich aber hat man die in entsprechenden mathematischen Ausdrücken auftretenden Minuszeichen wohl nur noch nicht der richtigen Größe zugeordnet (so wie es im heute als überholt geltenden Modell der Dirac Sea ja auch mal war).
Eine Zusammenstellung von Ergebnissen der Experimentalphysik, gegen die die String/M-Theorie (genauer: ein über sie gegebenes Modell) sich behaupten muss, findet man (sehr grob skizziert) hier.
Eine der bekanntesten Vorhersagen der M-Theorie ist sogenannte Supersymmetrie: Nach ihr gibt es zu jedem uns bisher bekannten Elementarteilchen, ja selbst zum Graviton, ein weit schwereres — seinen sog. Superpartner (SPartner). Obgleich die Experimentalphysik jene Teilchen bisher nicht nachweisen konnte, gehen die meisten Physiker davon aus, dass sie wirklich existieren. Ihrer hohen Masse wegen sind die meisten von ihnen durch Teilchenbeschleuniger heutiger Bauart aber ganz grundsätzlich nicht erzeugbar — das leichteste zu finden wäre schon ein Riesenerfolg. Man sucht nach ihm ...
Eine mir objektiv erscheinende Wertung der String/M-Theorie mit einer Liste von 12 Antworten, die man mit Hilfe dieser Theorie über vorher Bekanntes hinaus geben kann, findet sich in WikiBooks. Vier zentrale Fragen der Physiker, auf die es noch keine Antwort gibt und von denen heute auch niemand weiß, ob Stringtheorie sie je wird beantworten können, nennen diese Bilder.
Argumente, die stark dafür sprechen, dass Stringtheorie das bislang genaueste Modell der Physik liefert, sind:
- Für sehr große Objekte (wie etwa Himmelskörper) gehen die Gleichungen der Stringtheorie über in die der Allgemeinen Relativitätstheorie.
- Für extrem kleine Objekte (leichte Elementarteilchen etwa) gehen sie über in die der Quantenmechanik.
- Damit ist Stringtheorie das bislang einzig bekannte Modell, welches gleichermaßen für Makro- und Mikrokosmos passt.
- Zudem ist inzwischen gezeigt, dass viele Singularitäten der bislang besten Modelle sich auflösen unter den Gesetzen der Stringtheorie: "There is a growing list of situations that
would have left Einstein, Bohr, Heisenberg, Wheeler, and Feynman saying 'We just don't know what's going on', and yet for which string theory gives a complete and consistent description" (Zitat aus:
Brian Greene: The Hidden Reality, Vintage Books 2011).
Zum Schluss sei nicht vergessen zu erwähnen, dass es durchaus Fachleute gibt (wenn auch nur wenige), die der Stringtheorie sehr skeptisch gegenüber stehen:
- Oft genannt wird (wohl nur seines Buches wegen), der Mathematiker Peter Woit. Er geht so weit, zu sagen, dass Fördergelder, die an Stringtheoretiker gegeben werden, Geldverschwendung seien. Nachvollziehbare Argumente hat er allerdings nicht, und seine Behauptung, die Stringtheorie sei bisher nicht in der Lage gewesen irgendwelche Vorhersagen zu machen, ist definitiv falsch (siehe WikiBooks).
- Andere, wie etwa Roger Penrose, sind skeptisch, versuchen aber dennoch — wie es sich für Wissenschaftler gehört — objektiv zu bleiben und machen sich wenigstens die Mühe, den Stringtheoretikern ernsthaft zuzuhören.
- Einer von ihnen ist sicher auch Lee Smolin, der aber sieht vor allem deswegen wenig Sinn darin, Stringtheorie zu betreiben, da sie
sich in Bereiche vorwagt, in denen die Experimentalphysik wohl niemals wird Aussagen machen können (siehe dieses Interview mit ihm).
So zu argumentieren ist nachvollziehbar, zeugt aber vielleicht doch eher von fehlendem Mut, über bestehende Grenzen hinauszudenken.
Obgleich Smolins Beschreibung der Stringtheorie (und ihres Potentials) fast so begeistert klingt wie die von Greene, wird in Teil 2 seines Buches The Trouble with Physics (2006) doch klar, dass Stringtheorie noch sehr weit davon entfernt ist, mehr zu sein als ein gewaltiges Füllhorn für Ansätze neuer Ideen. Ein ähnlich konkretes Modell realer Physik wie Einsteins Relativitätstheorie und die Quantenmechanik es sind wird sie sicher noch lange nicht sein. Smolin sagt ganz klar: "... wir wissen immer noch nicht, wie die M-Theorie aussieht und ob es überhaupt eine Theorie gibt, die diesen Namen verdient". Durch ihn diskutierte Eckpunkte bisheriger Erkenntnisse (und das Ausmaß, in dem sie bisher eher nur Ansatz denn fertige Erkenntnis sind), lassen mich glauben, dass er recht hat — dies um so mehr, wenn man weiß, dass er selbst über Jahre hinweg in Stringtheorie geforscht und seine Ergebnisse in doch immerhin 18 Arbeiten veröffentlicht hat.
In Kapitel 12 seines Buches sagt er uns explizit, dass es bisher noch keinen allgemein anerkannten Vorschlag gibt, der zeigt, was denn nun eigentlich die Hauptgleichungen der Theorie sein sollen (!).
Fest steht auf jeden Fall: Nicht alles, was begeisterte Stringtheoretiker als schon erzielt bezeichnen, scheint durch ihre Theorie wirklich schon in vollem Umfange erreicht (Roger Penrose etwa nennt da als prominentestes Beispiel das Zusammenführen von Quantenmechanik und Allgemeiner Relativitätstheorie [siehe Seite 1011 seines 2008 erschienenen Buches The Road to Reality]. Lee Smolin konkretisiert das, indem er sagt, Stringtheorie ignoriere völlig die Tatsache, dass die Geometrie des Raumes zeitabhängig
ist. Und in der Tat: der vielen Massen wegen, die sich darin bewegen, ist seine Struktur sich ständig wandelnder Verformung unterworfen).
Wenn Stringtheorie recht habe, so sagt Smolin, müsse es eine noch elementarere Theorie geben, über die es dann gelingen könnte, die Stringtheorie hintergrund-unabhängig zu formulieren. Quantum Gravity — verwandt mit Twistor-Theorie (einer Idee von Penrose, die aber, wie Penrose selbst sagt, eher nur mathematischer Formalismus ist) — führt in diese Richtung:
Loop Quantum Gravity — eine Alternative zur Stringtheorie
Schleifen-Quantengravitation (Loop Quantum Gravity) gilt als die heute wichtigste Alternative zur Stringtheorie — eine Alternative aber, deren Vollständigkeitsanspruch eher bescheiden anmutet:Schleifen-Quantengravitation (siehe [1]) will zunächst nur Quantenmechanik und Gravitation unter einen Hut bringen — Stringtheorie aber hat ein allumfassendes Weltmodell zum Ziel (die Welt in ihrem Sinne ist der Kosmos als Ganzes; das vom Menschen bewohnte Universum, so erwartet man, wird sich dort als nur eines unter vielen möglichen einordnen).
Ein ganz gewaltiger Unterschied beider Theorien ist auf jeden Fall, dass die Stringtheorie von einem mindestens 10-dimensionalen Raum-Zeit-Kontinuum ausgeht, während Loop Quantum Gravity Zeit und Raum als quantisiert sieht (und nichts benötigt, was den 6 zusätzlichen Raumdimensionen entspricht, die die Stringtheorie vorhersagt — sie würden aber, sollte man sie doch finden, die Theorie der Quantengravitation keineswegs zu Fall bringen).
Wichtig: Der Spin-Schaum der Schleifen-Quantengravitation darf nicht verwechselt werden mit dem, was Physiker den Quantenschaum nennen (der erste existiert nur als theoretische Krücke, der zweite aber ist Teil physikalischer Realität).
Tatsache ist, dass sich heute wohl etwa 3-mal mehr Forscher mit Stringtheorie beschäftigen als mit Quantengravitation. In [S] sagt uns Lee Smolin, wie er darüber denkt. Beginnend etwa in der Mitte von Seite 3 seines Aufsatzes findet sich zudem ganz besonders gut verständliche erklärt, was zur Entdeckung dieser Theorie geführt hat, was Schleifen-Quantengravitation an Erkenntnissen (bis etwa 2003) schon gebracht hat, und auch worin sich ihr Weltbild von dem der Stringtheorie unterscheidet.
Beiden Theorien gemeinsam ist, dass ihr jeweiliges Modell der kleinsten Bausteine unseres Universums sich letztlich aus der Lösung gewisser Gleichungen ergibt, die schon bekanntes physikalisches Wissen zum Gegenstand haben:
- Bei Stringtheorie ist das ein äußerst komplexes, heute erst bruchstückhaft formuliertes System von Gleichungen, die bislang nur über Störungsrechnung (sog. perturbative Methodik) lösbar erscheinen.
- Der (Schleifen-) Quantengravitation aber liegt nur eine, zudem noch eher einfache Gleichung zugrunde: die sog. Wheeler-DeWitt-Gleichung. Eine recht umfangreiche Klasse ihrer Lösungen kennt man inzwischen genau.
Extrem interessant erscheint mir, was Smolin über die Kompatibilität beider Theorien mit einer kosmologischen Konstanten sagt: "... string theory seems to be incompatible with a world in which a cosmological constant has a positive sign, which is what the observations indicate. This is a problem that string theorists are thinking and worrying very hard about. They are resourceful people, and maybe they'll solve it; but as things stand at the moment [2003], string theory appears to be incompatible with that observation. ... loop quantum gravity [on the other hand] incorporates a positive cosmological constant extremely well. In fact it's our best case ..."
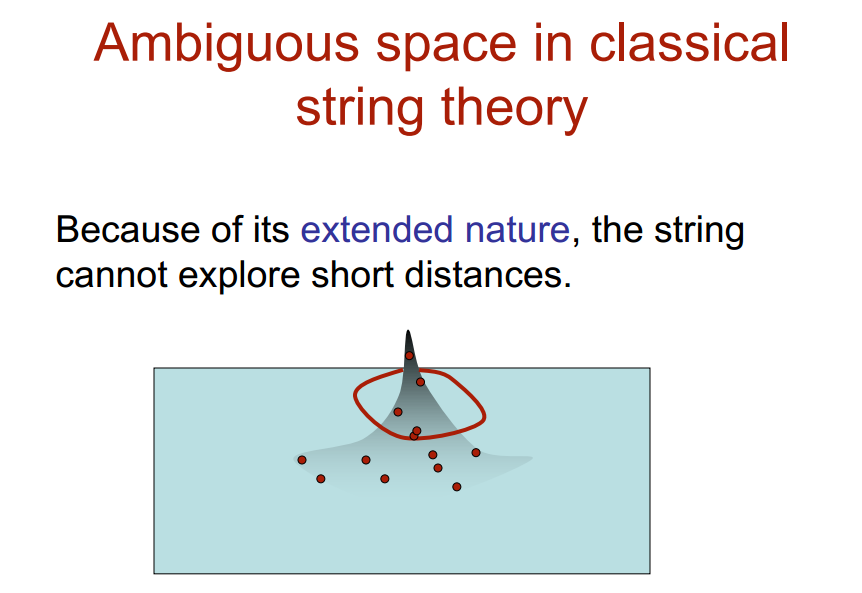
Wie Brian Greene auf den Seiten 390 und 391 seines Buches The Fabric of the Cosmos erläutert, gibt es seit 1995 Hinweise darauf, dass p-Branen nicht geschlossene Strings festhalten können — etwa so, wie Erwachsene kleine Kinder (und auch die ihre Geschwister) an die Hand nehmen können. Dies erinnert mich stark daran, dass auch im Modell der Quantengravitation die kleinsten Bausteine, in die sich alle Materie zerlegt (sog. Loops) nicht so existieren, dass sie nichts miteinander zu tun haben wollen, ganz im Gegenteil, sie scheinen sich irgenwie unterzuhaken:

Weaving space – the 3D structure of space in loop quantum gravity
can be visualized as a net of intersecting loops.
This simple model was built by Carlo Rovelli using key-rings, before spin networks and the physical significance of their nodes were discovered.
Note: The quantum theory of space-time in loop quantum gravity is really just a quantum theory of space. The spin network described by the theory cannot yet incorporate time. Some, such as Lee Smolin, believe that time will prove to be a necessary and fundamental component of the theory, while Carlo Rovelli believes that the theory will ultimately show that time doesn’t really exist, but is just an emergent property without a real existence on its own.
Gegenstand der Schleifen-Quantengravitationstheorie sind granulare Felder, welche Elementarteilchen und "Raumquanten" darstellen. Es gibt wahrscheinlichkeitsgetriebene Wechselwirkung zwischen ihnen, und die Wahrscheinlichkeit, dass etwas geschieht (ein Quantenereignis) lässt sich — das Geschehen bestimmter anderer Quantenereignisse vorausgesetzt — im Prinzip mit den Gleichungen der Theorie berechnen. Dieses netzartige Geflecht von Geschehen — man kann es die Raumzeit der Quanten nennen — kennt keine makroskopischen Begriffe von Raum und Zeit (in dem Sinne etwa, wie Einsteins Theorie sie kennt).
Die Raumquanten — Knoten im Gravitationsfeld — leben auf der Planckskala und können gesehen werden als die elementaren "Körnchen", aus denen sich die bewegliche Leinwand zusammensetzt, welche die Raumzeit im Sinne Einsteins darstellt.
Rovellis Gleichungen der Schleifentheorie sind moderne Fassung der Wheeler-deWitt-Gleichung — eine Gleichung, die alles Weltgeschehen regelt, ohne hierfür eine Zeitvariable zu benötigen.
Schleifen-Quantengravitation will keine umfassende, endgültige Theorie sein, keine "Weltformel", sondern wiill einfach nur eine kohärente Beschreibung der Welt liefern, wie Physiker sie bisher [vor allem auch auf kleinster Skala] verstanden haben. Dieses festgestellt zu haben, ist Rovelli wichtig.
Diese Theorie — so Rovelli — beschreibt Quantendynamik, welche von sich aus weder Raum noch Zeit kennt: nur Ereignisse und Beziehungen zwischen ihnen.
Was Rovelli in 2012 über String Theorie denkt, sagt uns sein Papier [A critical look at Strings]: Es gilt eigentlich immer noch das in 2003 Gesagte.
Man lese auch: Loop Quantum Gravity – a Status Report (Jan 2012) und Quanten der Raumzeit.
Carlo Rovelli (s. seine Antwort auf Seite antwortenhier.me) sieht keine Möglichkeit, Loop Quantum Gravity mit Stringtheorie zu kombinieren. Beide Theorien seien einfach zu verschieden. Er nennt wesentliche Unterschiede, diese Meinung zu begründen.
Soweit die Experimentalphysik bisher versucht hat, Quantelung von Raum und Zeit nachzuweisen, fand man eher Hinweise, die dafür sprechen, dass solche Quantelung NICHT existiert. Mehr dazu gegen Ende eines populärwissenschaftlich gehaltenen Aufsatzes aus 2003.
Relativitätstheorie im Rahmen der Stringtheorie
Der Astrophysiker Günter Spanner macht auf Seite 251-252 seines Buches » Das Geheimnis der Gravitationswellen « (2016) darauf aufmerksam, dass sich aus der Stringtheorie eine verallgemeinerte Feldtheorie ableiten lässt, in der ein freier Parameter auftritt. Wählt man ihn unendlich groß, reduziert sich das entsprechende Gleichungssystem auf genau das von Einsteins Allgemeiner Relativitätstheorie (so dass die Stringtheorie sozusagen eine erweiterte Alternative zu Einsteins Theorie umfasst).Tatsache sei aber auch: Wer sich eingehend mit solchen Varianten befasst, gilt schnell als wissenschaftlicher Außenseiter. Renommierte Fachzeitschriften nehmen entsprechende Arbeiten meist gar nicht erst zur Publikation an, etablierte Wissenschaftler sprechen fast nie darüber.
Fragen zur wahren Natur von Raum und Zeit
Die Theorie der Schleifenquantengravitation ist beispielsweise eine hintergrundunabhängige Theorie, da sie keinen Raumzeithintergrund annimmt, sondern ihn durch die Theorie erst konstruiert.Die derzeitigen stringtheoretischen Ansätze gehen dagegen davon aus, dass Strings sich schwingend durch eine gegebene Raumzeit bewegen, die 'von Hand' in die Theorie eingefügt wird. Daher ist die Stringtheorie momentan noch nicht hintergrundunabhängig.
Der Stringtheoretiker Brian Greene hofft jedoch, dass es in Zukunft gelingen wird, die hintergrundunabhängigen Techniken, die in der Schleifenquantengravitation eingesetzt werden, auf die Stringtheorie zu übertragen. Ob das gelingen wird, ist derzeit aber noch nicht abzusehen.
Interessant wäre auch, zu untersuchen, ob sich die Stringtheorie nicht dahingehend abändern lässt, dass man Elementarteilchen nicht mit möglichen Schwingungszuständen gedachter Fäden (Strings) identifiziert, sondern stattdessen mit denkbaren Schwingungszuständen sich durch den Raum ausbreitender Kugelwellen. Das zu versuchen liegt nahe und könnte Sinn machen, da sich Photonen oder Gravitationswellen ja tatsächlich als Kugelwellen durch den Raum ausbreiten.
Sollte Abändern der Stringtheorie zu so einem Kugelwellenmodell möglich sein, wäre die so entstandene Theorie Carlo Rovellis Schleifenquantengravitationsmodell schon recht ähnlich.
Wie oben schon gesagt, gibt es Forscher und Forschungs-Richtungen der Theoretischen Physik, die uns hinführen zur Vermutung, dass Raum und Zeit nur gedankliche Abstraktion sein könnten, in Wirklichkeit also zurückzuführen wären auf möglicherweise nur ein einziges, weit fundamentaleres Konzept.
Dahingehende Hinweise kommen aus wenigstens fünf völlig unterschiedlichen Richtungen:
- Schleifen-Quantengravitation ist der (bislang wohl einzige) konstruktive, völlig revolutionäre Ansatz nach dorthin.
- Einsteins allgemeine Relativitätstheorie — unser bislang tiefstes Wissen über die Natur von Raum und Zeit — kommt als Aussage aus einem Gleichungssystem, von dem der Zeitforscher Julian Barbour sagt, dass noch keineswegs all seine Aussagen schon bekannt, systematisch untersucht oder gar voll gewürdigt sind (ein Buch, an dem er 2011 noch schreibt, soll den Fachleuten mehr dazu sagen und könnte sein Lebenswerk zusammenführen zu etwas, das uns wirklich auf ein völlig neues, unerwartetes Verständnis der Zeit führt).
Neben solch konstruktiven Ansätzen gibt es Beobachtungen, die Physiker einfach nur vermuten lassen, dass der Mensch die wahre Natur von Raum und Zeit noch nicht verstanden hat. Dazu zählen (siehe das letzte Kapitel von Brian Greenes Buch The Fabric of the Cosmos):
- Gewisse Erkenntnisse aus der Theorie der Schwarzen Löcher (genauer: die durch Bekenstein und Hawking entdeckte Tatsache, dass die maximal mögliche Entropie schwarzer Löcher proportional zur Fläche ihres Ereignishorizonts ist, also nicht — wie man vermuten könnte — proportional zu ihrem räumlichen Volumen).
- Gewisse Symmetrie-Eigenschaften der Stringtheorie (genauer: die Tatsache, dass die Stringtheorie uns zu Weltmodellen führt, die identische Physik bedeuten obgleich sie zueinander nicht isomorphe Geometrie haben).
- Unser Wissen über das holographische Prinzip (nach dem Weltmodelle sogar dann noch äquivalent sein können, wenn sie der Welt unterschiedlich viele Dimensionen zugestehen. Stringtheorie liefert tatsächlich auch solche Paare).
Auf Seite 485 in The Fabric of the Cosmos sagt Greene: "More and more, these clues point toward the conclusion that the form of spacetime is an adorning detail that varies from one formulation of a physical theory to the next, rather than being a fundamental element of reality. Much as the number of letters, syllables, and vowels in the word cat differ from those in gato, its Spanish translation, the form of spacetime — its shape, its size, and even the number of its dimensions — also changes in translation.
Eine ganz ähnliche Frage
Was mich an der Stringtheorie am meisten irritiert ist die Tatsache, dass nach ihr unsere Welt — als eine Welt mit mindestens N = 3 Dimensionen — sich zerlegen sollte in kleinste Teile (Strings bzw. Membranen), deren jeder durchaus auch eine Dimension kleiner als 3 haben kann. Das aber — so denke ich — ist nur dann möglich, wenn es sich um rein abstrakte Teilobjekte handelt (um solche also, die gedankliche Projektion real existierender Objekte der vollen Dimension N sind; Was aber, so frage ich, macht dann für angeblich real existierende Strings den Unterschied aus, der ihnen diese höhere Dimension gibt?).Betrachten wir zwei Beispiele:
- Ein Punkt in einem 3-dimensionalen Raum ist — als 0-dimensionales Objekt (als Objekt also, das keine Ausdehnung hat) — ganz klar nur Abstraktion.
- Die Oberfläche einer anfassbaren Kugel ist zwar anfassbar, als Raum der Dimension 2 aber dennoch nur ein Abstraktum. Konkretes Objekt ist sie nur als 3-dimensionaler Teil der Kugel (wenn man die als konkret und somit ebenfalls 3-dimensional vorliegen hat).
Was also bedeutet reale Existenz denn nun genau? Und macht diese Frage für theoretische Physiker denn überhaupt Sinn?
Mir scheint, es macht wohl eher nur Sinn zu fragen, ob wir ein betrachtetes physikalisches Objekt mit Sicherheit als Instanz eines bestimmten Typs sehen können (wo dieser Typ dann aber auf jeden Fall Abstraktion ist — sprich: eine Summe bestimmter Eigenschaften, deren jede nur Abstraktion ist).
Jedes Modell unserer Welt ist notwendigerweise eine Menge solcher Typen und eine Menge von Regeln, die sagen, wie sie aufeinander aufbauen, wie Instanzen interagieren, und welche Freiheiten jene Instanzen haben, sich hinsichtlich der Werte ihrer Eigenschaften fortzuentwickeln.
Ein wohldefiniertes allen anderen überlegenes Modell unserer Welt gibt es wohl ebensowenig wie eine Sprache, die allen anderen Sprachen überlegen ist: Jedes Modell ist nur ein bestimmte Sprache, und den Wortschatz einer Sprache bijektiv auf den einer anderen abzubilden, ist stets nur grob möglich.
Weiterführende, allgemein verständliche Literatur
- Cumrun Vafa weckt Zweifel am stringtheoretischen Weltmodell (2018)
- Strings oder Schleifen? — welche der beiden konkurrierenden Theorien wird gewinnen?
- Stringtheorie — Wie man sie fand und wo man jetzt steht
- Stringtheorie — Eine populärwissenschaftliche Einführung
- Stringtheorie — Erfolge und Probleme
Scheinbar hat die Dimension der zugrundeliegenden Minkowski-Raumzeit (MRZ) mit der Quantisierung der Strings zu tun. Man bezeichnet die Zahl der Raumzeit-Dimensionen, die notwendig sind, einen String quantisieren zu können, als kritische Dimension.- Einen bosonischen String zu quantisieren benötigt man eine MRZ-Hintergrundraumzeit der Dimension 26.
- Quantisierung fermionischer Strings ist, so sagen Experten, nur möglich, wenn die Dimension der MRZ-Hintergrundraumzeit 10 beträgt.
- Aus technischen Gründen impliziere SUSY+Strings die Dimension 10.
- Stringtheorie — Wie viele Dimensionen hat unsere Welt?
- Stringtheorie — The 2nd String Revolution
- Stringtheorie — können Strings und Branen ganze Universen sein?
- Stringtheorie — vom Mathematischen her, siehe auch: M-Theorie und die E(10)-Symmetrie
- Stringtheorie — worum es geht und Widersprüche, die eine Weltformel zu klären hätte
- Stringtheorie — FAQs and more
- Unterscheide F-Strings von Dp-Strings
Dass die 3 Typen von Hadronen — Nukleonen, Mesonen und Glueballs — stringartige Objekte sind, ist inzwischen anerkannte Tatsache: Laborexperimente, welche die hadronische Stringtheorie untermauern, kennt man nun schon seit fast einem halben Jahrhundert. Strings, die als Glueballs (= Ketten von Gluonen) die Hadronen bilden, nennt man QCD-Strings.
- Strings, Membranen und Dualitäten sowie Witten: Perspektiven der Stringtheorie (1999)
- String Theory as of 2001 (see also [F] and [D])
- 2011: Simulation confirms the existence of 9 spacial dimensions (in the model)
ABER: Ob der Kosmos überhaupt eindeutig bestimmbare Dimension hat, ist eine Frage, die sich Physiker mehr und mehr wirklich stellen.
In engem Zusammenhang mit dieser Frage stehen erstaunliche Eigenschaften sog. Dualitätskonzepte (gut erklärt durch Michio Kaku in M-Theory: The Mother of all SuperStrings).
- Quantum Superposition
and Quantum Entanglement / Quantenverschränkung
Man beachte: Obgleich man 2007 im Experiment zeigen konnte, dass zwei verschränkte Photonen bezüglich verschiedener Eigenschaften, u. a. ihrer Polarisation, sich mit wenigstens 10.000-facher Lichtgeschwindigkeit synchronisiert haben, gilt weiterhin, dass Informationsübertragung schneller als das Licht nicht möglich ist.
Der Grund hierfür: Obgleich miteinander verschränkte Photonen sich stets synchron zueinander in einen neuen Zustand begeben, kann man den nicht vorgeben. Das Quantum selbst wählt ihn, der Physiker aber kennt für jede mögliche Wahl nur die Wahrscheinlichkeit ihres Eintretens.
- Quantum Entanglement:
[explained+at RatWiki]
[made visible], [across time]+[T]+[ZV], [in biology], [as of 2010+2011+2012], [applications], [1st quantum network], [questions answered] [and more ...], - Ein Quantenwelt-Experiment, das die Vergangenheit beeinflusst (2012)
Was er hier im Experiment fand, so sagt Zeilinger, bedeute letztlich, "dass ein Quantencomputer in der Vergangenheit mit einem Problem zu rechnen beginnen kann, von einem Input, der erst in der Zukunft existiert".
Das, so denke ich mir, könnte in Zusammenhang stehen mit der auf Hugh Everett III zurückgehenden Viele-Welten-Interpretation — vielleicht ist ja auch unser Durchwandern der Zeit nichts anderes als ein ständiges Hinüberwechseln in eine weitere, parallel existierende Welt. Wenn dem so wäre, könnte man vielleicht doch irgendwann erkennen, dass vergangene und zukünftige Versionen unserer Welt ebenso real sind wie jene, in der wir uns eben jetzt (nur ein Zeitquantum lang) befinden.
Dürfte man dann aber wirklich davon ausgehen, dass der Zeittakt, den unterschiedliche Elementarteilchen erleben, derselbe ist? Wahrscheinlich nicht.
Das aber würde vermuten lassen, dass die Zeit von eben derselben Natur sein könnte wie der Raum im Sinne der Schleifen-Quanten-Gravitation. Sie würde dann letztlich — real also — gar nicht existieren (eine Vermutung, für die ja auch das Zwillings-Paradoxon spricht).
- Quantum Entanglement:
[explained+at RatWiki]
- Greg Egan's Homepage (containing quite interesting explanations for Beginners)
- Einstein for Everyone (eine Vorlesung, nicht besonders gut)
- Themen Theoretischer Physik (gut erklärt im Blog eines Physikers)
- Characteristics of a Photon (a very good explanation of what a photon actually is)
- Über die Asymptotische Freiheit der starken Wechselwirkung, siehe auch [AW]
- Cosmology for Beginners
- Den Urknall richtig verstehen
- Bartelmanns auch an Laien gerichtete Aufsätze über kosmologische Erkenntnisse
- Big Bang Theory: Details of the two Tales
- What are Dark Energy and Dark Matter? (see also Greene's Explanation)
- Brian Greene on: Did we find the Higgs Particle?
- Über Heisenbergs Unschärfe-Relation,
genauer in [U]
Die Eigenschaft von zwei einander als präzise ausschließender Eigenschaftswerte nennt man Komplementärität, und es gibt tatsächlich zu wirklich jeder quantifizierbaren Eigenschaft eines physikalischen Objekts wenigstens eine dazu komplementäre.
Niels Bohr erkannte, dass Unschärfe in diesem Sinne eine fundamentale Eigenschaft unserer Welt ist: Sie setzt keineswegs nur unserem Wissen eine Grenze, sondern ist auch eine Grenze dafür, wie genau ein physikalisches Objekt denn überhaupt einen bestimmten Zustand haben kann.
Einstein allerdings sah das anders: Für ihn war diese Unschärfe wirklich nur eine unvermeidbare Beobachtungsgrenze. Für Philosophen sind beide Auffassungen verträglich, denn ihnen gilt als existent nur, was sich — prinzipiell wenigstens — auch beobachten lässt.
Die mir am ehesten einleuchtende Begründung der Unschärfe-Relation und ihrer Interpretation im Bohrschen Sinne fand ich auf den Seiten 82-84 von Anton Zeilingers Buch Einsteins Spuk.
- Das holographische Prinzip
- Über kleinste Strukturen und Raumzeit: Grain by Grain
- The case for background independence (Lee Smolin, 2008)
- Three Roads to Quantum Gravity (Lee Smolin, 2002)
- Zur Geschichte der Idee Is Time an Illusion?
- Does Time exist? – Julian Barbour on a possibly next Revolution in Physics. See also [his current work].
- Alain Connes: Begründer der nicht-kommutativen Geometrie, die — nach Lee Smolins Meinung —
zu einem wichtigen Werkzeug der Theoretischen Physik werden könnte.
Nichtkommutative Geometrie ist weiteres Indiz für eine geheimnisvolle Verwandtschaft mathematischer und physikalischer Gesetzmäßigkeiten: Formuliert man nämlich Maxwells Theorie des Elektromagnetismus im Rahmen der einfachsten nichtkommutativen Geometrie, so ist man beim Weinberg-Salem-Modell, welches den Elektromagnetismus mit der schwachen Kernkraft zusammenführt. Mit anderen Worten (so schreibt Smolin): "Die elektroschwachen Wechselwirkungen und die Higgs-Felder treten automatisch und korrekt zutage."
- Bisher bemerkenswerteste Anwendung der Schleifen-Quanten-Gravitation (kurz Loop-Theorie) ist Bojowalds Theorie den Urknall betreffend.
- Sollte der Raum gequantelt sein, muss 10-34 Meter eine obere Grenze für die Größe der Raumquanten sein.
Bestätigt Stringtheorie Einsteins Gravitationstheorie?
» The Official String Theory Website « sagt: "Superstring theory does not predict that the Einstein equations are obeyed exactly. String theory adds an infinite series of corrections to the theory of gravity. Under normal circumstances, if we only look at distance scales much larger than a string, then these corrections are not measurable. But as the distance scale gets smaller, these corrections become larger until the Einstein equation no longer adequately describes the result."Claus Kiefer in Quantenkosmos: Superstringtheorie ist notwendigerweise die 11-dimensionale Version der Stringtheorie. (Lies auch Abschnitt 4.1 in Schwarz).
Gibt es wirklich versteckte Raumdimensionen?
Tatsache ist: Stringtheorie sagt wohl nichts aus über die Zahl der Dimensionen unserer Welt. Kaku erklärt: In vielen unendlichen Summen der Stringtheorie trete ein Term auf, der nur dann verschwindet, wenn man – in der bosonischen Stringtheorie – von 26 Dimensionen ausgehe. Sie reduzieren sich auf 10, wenn man der Stringtheorie zusätzlich noch Supersysmmetrie unterstellt. M-Theorie (eine noch unbekannte, nach Witten mögliche Vereinigung sämtlicher Stringtheorien) müsste eine Dimension mehr haben. Einzig und allein das ist der Grund, warum man heute von "supersymmetrischer, 11-dimensionaler Stringtheorie" spricht und die GUT-Theorien als in der Stringtheorie mit berücksichtigt sieht.Penrose's Twister Theory in the Light of M-Theory
In 2003 Edward Witten came up with an astonishing new paper which related string theory with twistor geometry. Two years later (Jan 2005) he found arguments that strings may not need all those extra dimensions after all. Wittens work sparked a whole slew of papers from his fellow theorists and interest is still growing.Witten himself is not convinced yet: "Twistor string theory is something that only partly works", he says. Nevertheless, his ideas have infused new life into research on merging the ideas from these two theories. It turns out that a twistor string theory may be able to simplify the computation of scattering amplitudes from the Feynman diagrams. But so far the discovery offers only a partial description of the possible processes at the LHC.
George Musser (2010): » Whether or not they succeed in remaking space and time, twistorians and string theorists have already endeared themselves to particle physicists. Even fairly simple particle collisions demand equations containing tens of thousands of terms, which are written using a strategy devised by Richard Feynman in the 1940s. Though most of those terms end up canceling out, you do not know in advance which will cancel, so you have to slog through all of them. An alternative strategy inspired by twistors and strings captures symmetries that Feynman’s approach does not, so it sheds the excess mathematical baggage from the outset. Calculations that math whizzes once gave up on now take just a couple of weeks. I’m pretty sure Feynman would be quite pleased if he saw what we can do, says Zvi Bern of the University of California, Los Angeles. «
Nochmals zur Suche nach der Weltformel
Ganz offensichtlich gilt, was Smolin uns sagt:Wenn die Stringtheorie oder die Schleifen-Quanten-Gravitation die Lösung selbst wären,
würden wir es inzwischen wissen.
Sie mögen Anhaltspunkte sein, kleine Teile der Antwort, sie mögen wichtige Erkenntnisse enthalten,
sind aber keinesfalls mehr.
Die Stringtheorie kann die Elementarteilchen, also letztlich die Materie, besser beschreiben, hat aber Schwierigkeiten mit Raum und Zeit. Die Loop-Theorie dagegen ist eine Theorie von Raum und Zeit, bekommt aber die Materie bislang nicht in den Griff. Vielleicht muss man beide eines Tages kombinieren ...
Es soll auch nicht verschwiegen werden, dass es Physiker gibt, die rein gar nichts von Stringtheorie halten (so z.B. H. Dieter Zeh).
Witten dagegen meint: Unlike conventional quantum field theory, string theory requires gravity. I regard this fact as one of the greatest insights in science ever made.
In 2005 schrieb Witten dann aber auch:
-
But what is string theory? It may well be the only way to reconcile gravity and quantum mechanics, but what is the core idea behind it?
Einstein understood the central concepts of general relativity years before he developed the detailed equations.
By contrast, string theory has been discovered in bits and pieces — over a period that has stretched for nearly four decades — without anyone really understanding what is behind it.
As a result, every bit that is unearthed comes as a surprise. We still don't know where all these ideas are coming from — or heading to.
Interessant ist, dass Leonard Susskind – er gilt schon seit 1969 als einer der Pioniere der Stringtheorie – heute nicht mehr glaubt, dass Stringtheorie unsere Welt korrekt beschreiben kann: Wir leben in einem de-Sitter-Raum, er aber sei zunehmend davon überzeugt, dass sämtliche durch Stringtheorie beschreibbaren Räume anti-de-Sitter sind. Note: Wirklich bewiesen scheint Letzteres bisher aber nicht zu sein.
Tatsache also ist, dass viele – aber keineswegs alle – Stringtheoretiker Susskinds Meinung nachvollziehbar finden. Richtig ist auf jeden Fall, dass es bisher niemand gelang, eine überzeugende de-Sitter-Lösung aus der Stringtheorie abzuleiten.
Genau genommen kann man auch gar nicht mit absoluter Sicherheit ausschließen, dass unser Weltraum nicht vielleicht doch AdS (= anti-deSitter) ist: Beobachtetes, lokales Krümmungsverhalten muss ja nicht unbedingt auch weiträumig gegebenes sein. Mit anderen Worten: Wir werden nie mit absoluter Sicherheit ausschließen können, dass der Weltraum nicht doch hyperbolische Geometrie hat, also – weiträumig gesehen – ewig expandieren könnte.
Auch Polchinskis Antwort auf die Kritik von Smolin und Woit sollte man zur Kenntnis nehmen.
Wo wir derzeit stehen, beschreiben sehr schön einige Vorträge von Nathan Seiberg. Er stellt dort z.B. fest:
stw5832STD — Stringtheorie . Theorie . Dimensionen — News?
Mehr + B G E + S H A + More
Stringtheorie deuten
Wie Stringtheorie Einsteins Weltmodell (die ART) verallgemeinert
M-Theory as of 1998
2023 im Gespräch mit Edward Witten
Witten's Homepage
Witten's Assassment of Stringtheory — Man lese das auf jeden Fall
Stringtheorie um 2000
Stringtheorie in Kurzfassung (2016)
Geschichte und Bewertung von Stringtheorie und Schleifenquanten-Gravitation
Grenzen der Stringtheorie
Was man mindestens wissen sollte — auch was Überprüfbarkeit der stringtheoretischer Ergebnisse betrifft
Bisher machen nur Dualitäten Stringtheorie zu M-Theorie
Kosmische Strings
Wie sich Stringtheorie mit der Inflationstheorie veträgt
Viewpoints on String Theory
AdS/CFT: Are Quantum Field Theory and String Theory equivalent?
Lisa Randall's Theory on Brane Gravity (2003)
SUSY, SUGRA und Stringtheory
String theory: Is dark energy even allowed?
Grundlagen der Stringtheorie
TU Dresden: Stringtheorie
Wo vier führende theoretische Physiker unserer Zeit (2024) miteinander diskutieren:
Unifying Nature’s Laws: The State of String Theory
Is string theory a failing model?
The String Theory Wars and What Happened Next
Roger Penrose: "String Theory is Wrong And Dark Matter Doesn't Exist"