Falsches, Korrektes und Nachdenkenswertes
Eine Situation S heißt paradox, wenn sie dazu führt, dass es eine Aussage A gibt derart, dass die Annahme, A sei wahr, ebenso zu einem Widerspruch führt, wie die Annahme, A sei falsch.Der in der Mathematik so häufig verwendete Beweis durch Widerspruch ist ein Beweisweg, der nicht mehr anwendbar ist, sobald man eine paradoxe Situation vorliegen hat. (Ein Beweis durch Widerspruch – auch indirekter Beweis genannt – besteht darin, zu sagen, eine Aussage sei bewiesen, sobald man aus der Annahme, sie sei falsch, einen Widerspruch ableiten kann.)
Die Mathematik bewegt sich insofern auf gedanklichem Glatteis, als kein Mathematiker – bevor er einen Beweis durch Widerspruch führt – zunächst mal zeigt, dass keine paradoxe Situation vorliegt.
Die nun folgende Diskussion soll dem Leser einen Eindruck vermitteln, welche Denkfehler i.A. zu dem führen, was man dann eine Paradoxie nennt:
Seit nun schon etwa 2500 Jahren diskutiert man immer wieder das sog. Lügner-Paradox. Wo an solcher Diskussion keine Logiker beteiligt sind, wird die betrachtete Situation S dann aber oft schon rein sprachlich zu ungenau beschrieben (mit dem Ergebnis, dass sie – bei genauem Hinsehen – dann eben doch nicht paradox ist). Hier ein oft anzutreffendes, typisches Beispiel:
Als kleine Denkübung beweisen wir, dass hier keine Paradoxie vorliegt: Sei dazu AKL die Aussage "Alle Kreter lügen".
Zunächst fällt auf, dass AKL gar keine wohldefinierte Aussage ist – und zwar deswegen nicht, weil der Begriff des Lügens unterschiedlich definiert sein kann: Sagt man, dass ein Kreter lügt, wenn er hin und wieder absichtlich Falsches behauptet? Oder interpretieren wir die Aussage, er lüge, dahingehend, dass er stets die Unwahrheit sagt?
Macht man sich die erste Definition zu eigen, d.h. versteht man die Aussage so, wie sie ganz offensichtlich vom ursprünglichen Autor gemeint war – wahrscheinlich Epimenides von Kreta (gut 600 Jahre vor Christus) – so führt sie keineswegs zu Widersprüchen.
Macht man sich dagegen die zweite Definition zu eigen, so sollte man sich, schon der Ehrlichkeit wegen, auch entsprechend genau ausdrücken; etwa so:
Aber selbst in dieser Form ist nicht klar, was zu lügen denn eigentlich bedeutet. Soll es bedeuten, subjektiv Falsches auszusagen, oder soll es bedeuten, objektiv falsche Aussagen zu machen? Beispiel: Bei Bäcker B kostet jede Semmel 25 Cent. Person P denkt, der Preis wäre 30 Cent, will eine Person C anlügen und sagt daher: "Bei Bäcker B kosten alle Semmeln 25 Cent". Hat P dann gelogen? Die Antwort ist nicht eindeutig, denn subjektiv gesehen hat P gelogen, objektiv gesehen aber war, was er C erzählt hat, richtig.
FALL 1: Zu lügen bedeute, ausschließlich objektiv falsche Aussagen zu machen. Gemeint ist dann:
Die Annahme, A sei wahr, führt wegen S zu NOT AKL. Das aber bedeutet, dass nicht immer das Gegenteil von dem gilt, was ein Kreter sagt. Über den Wahrheitsgehalt einer bestimmten Aussage eines Kreters sagt dies aber gar nichts aus. Die Annahme, A sei wahr, führt demnach zu keinem Widerspruch, und so ist S nicht paradox.
FALL 2: Zu lügen bedeute, stets subjektiv falsche Aussagen zu machen (sprich: stets das Gegenteil der eigenen Meinung zu sagen). Präzise ausgedrückt bedeutet das
Auch hier führt die Annahme, A sei wahr, wegen S zu NOT AKL, also wieder zu einer Aussage, die über den Wahrheitsgehalt einer konkreten Aussage eines Kreters gar nichts aussagt. Somit kann auch in diesem Fall S über A nicht als paradox eingestuft werden.
Hinweis: Genau genommen bleibt jetzt die Frage, ob nicht A durch eine andere Aussage ersetzt werden kann, die dann möglicherweise S als paradox erkennbar macht. Irgendwelche Hinweise darauf, dass das möglich ist, sind jedoch nicht erkennbar.
Wir sehen: Die Aussage "Ein Kreter sagt: Alle Kreter lügen" ist weder wohldefiniert, noch paradox. Russel (1872-1970) hat das erkannt, dann aber doch wirkliche Paradoxa gefunden:
Nimmt man an, S sei falsch, so ist S wahr – ein Widerspruch. Nimmt man umgekehrt an, S sei wahr, so ist S falsch – auch ein Widerspruch.
Für den Logiker interessant ist, dass die hier vorhandene Rückbezüglichkeit der Aussage auf sich selbst beliebig versteckt auftreten kann. Hier ist ein Beispiel, bei dem sie erst in Kombination zweier Aussagen zustande kommt:
Ausgehend von diesem Beispiel kann man sehr schnell zeigen, dass es zu jeder positiven ganzen Zahl N eine Menge von N Aussagen gibt, die in ihrer Kombination – und auch wirklich erst in Kombination aller N Aussagen – zu solcher Rückbezüglichkeit führen (und als Folge davon dann zu unauflösbaren Widersprüchen).
Wählt man z.B. N = 3.000.000.000, so wird klar, wie versteckt logische Widersprüche sein können und wie schwierig es dann wird, eine Menge gegebener Aussagen als paradox zu erkennen.
Russel hat zudem gezeigt, dass neben Aussagen auch Definitionen – solche, wie fast jeder moderne mathematische Beweis sie enthält – absolut unbrauchbar sein können. Die wohl am häufigsten anzutreffenden mathematischen Definitionen sind Definitionen der Art
Russels Beispiel war:
Er betrachtete dann die Frage, ob M sich selbst als Element enthält und stellt fest: Welche Antwort auch immer man gibt, sie führt zu einem Widerspruch. Diese Definition ist demnach unbrauchbar (da paradox). Und wieder gilt: Die Tatsache, dass eine solche Definition keinerlei Sinn macht, kann beliebig schwierig zu erkennen sein.
Wer also versucht, ein Konzept zu definieren, um dann irgendwelche Aussagen darüber zu erarbeiten, der sollte zunächst beweisen, dass so definierte Modelle auch wirklich existieren. Ansonsten könnte es ihm gehen wie jenem unglücklichen Doktoranden, dessen Dissertation unendlichdimensionale lokalkompakte Vektorräume zum Gegenstand hatte. Er wusste nicht, dass es solche gar nicht geben kann (Andre Weil: Basic Number Theory, Springer-Verlag New York 1973, Seite 6, Corollary 2). Die Tatsache, dass das damals schon bewiesen war, ist unerheblich: Denn selbst wenn er sein Werk geschrieben hätte, noch bevor es den genannten Beweis gab, wäre sein Ergebnis ohne jeden Sinn gewesen — ohne dass man das hätte erkennen können (!).
Sicher nicht dieses Beispiel, wohl aber die beiden Tatsachen, dass
- in einer gegebenen Menge von Aussagen Paradoxie beliebig schwierig erkennbar sein kann und
- wenn sie denn vorhanden ist, der so überaus häufig genutzte indirekte Beweis gar nicht mehr schlüssig ist
Hinweis: Es gibt heute mathematische Beweise, welche sich über ganze Bücher hinweg erstrecken und über mehrere mathematische Teilgebiete hinweg, so dass eine Person alleine so einen Beweis gar nicht mehr in all seinen Details verstehen kann (der moderne Beweis zu Fermat's letztem Satz etwa ist von dieser Art). Die Wahrscheinlichkeit, dass in derart komplexen Beweisen irgendwo unentdeckt ein Fehler steckt, scheint entsprechend hoch. Kann man solcher Mathematik dann aber wirklich noch so ganz bedingungslos vertrauen?
Intuitive Paradoxie (die nur sprichwörtliche):
Was man darunter versteht, wird am ehesten klar an einem Beispiel:Wissenschaftliche Untersuchungen (z.B. eine der Carnegie Mellon University aus 2003) belegen, dass moderne Software, wenn sie in Betrieb genommen wird, i.A. immer noch bis zu fünf Fehler pro 1000 Lines of Code enthält; sprich: etwa 1 Fehler auf je 3 DIN A4 Seiten manuell erstellten Source Codes. Selbst im besten untersuchten Programm – bestehend aus 10.000.000 Lines of Code – fand sich immer noch 1 Fehler in je 7500 Zeilen. Wirklich vorhanden waren wohl mehr, denn in großen Systemen entdeckt man niemals alle. Wären mathematische Publikationen auch nur annähernd so fehlerhaft, wäre die Mathematik als Wissenschaft längst in sich zusammen gebrochen (es baut dort ja Neues stets auf Älterem auf).
Wir sehen: Die Informatik — wenigstens aber ihre Technik zur Qualitätssicherung — steckt heute wohl noch in Kinderschuhen, die vergleichbar sind mit denen, die die Mathematik noch vor Christi Geburt trug. Auf jeden Fall ist sie noch weit davon entfernt, so zuverlässig zu sein, wie Mathematik das sein möchte (und i.A. auch wirklich ist).
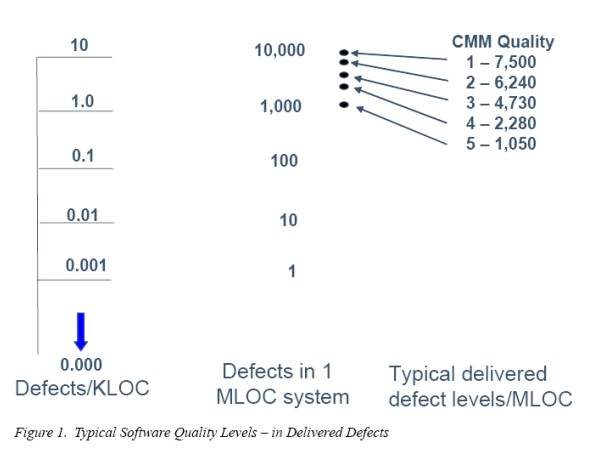
Quelle: Carnegie Mellon University, 2003
zitierend
C. Jones: Software Assessments, Benchmarks, and Best Practices. Addison Wesley, 2000.
Siehe auch neuere Untersuchungen

Quelle: Carnegie Mellon University, 2010
Wirklich paradox an dieser Situation ist, dass die Software-Industrie diesen Zustand weitgehend als natürlich betrachtet, obgleich man sehr genau weiß, dass die Kosten für die Behebung eines Fehlers um einen Faktor zwischen 10 und 100 größer sind als notwendig, wenn er erst nach Auslieferung an den Kunden entdeckt wird:
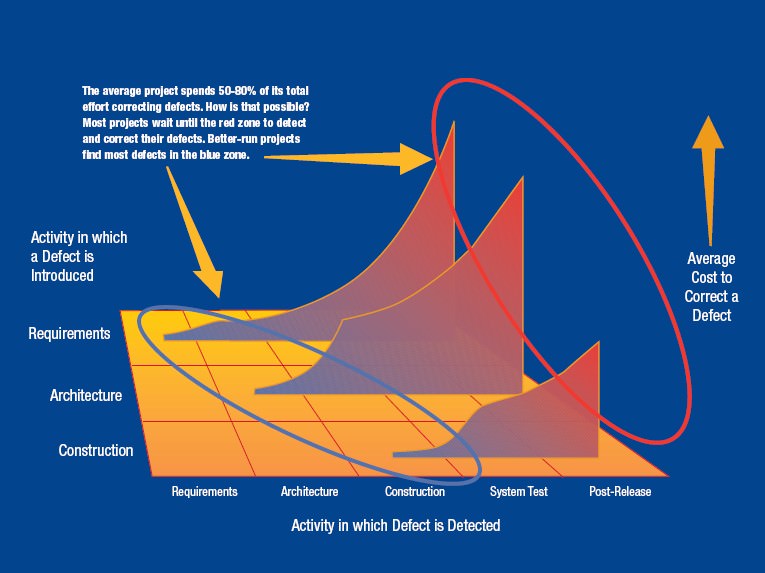
Mistakes are unavoidable, but studies over 25 years have proven that it pays to remove defects as early as possible: Purging requirements and architecture errors before detailed construction begins reduces rework costs by 90-99% compared to correcting those errors during system test or after release.
Quelle: Construx, 2011 und Fehlerkosten
Siehe auch:
- Wenn man Häuser bauen würde wie man Software entwickelt ...
- Wie erfolgreich Software-Entwickler um die Jahrtausendwende waren
- Millionen in den Sand gesetzt ... (Beispiele ab 2006)
stw4525AKB — Aussage . Kreter . Beweis — News?
Mehr + B G E + S H A + More