Einstein und seine Gravitationstheorie (die ART)
 
oder:
 

Was Kritiker der Stringtheorie allzu oft übersehen

 
 
 
In seinem — übringens äußerst lesenswerten — Buch Raum-Zeit (de Gruyter, 2009) analysiert Martin Carrier

• nicht nur, welche Grundüberlegungen Einstein zu dem geführt haben, was wir heute seine Allgemeine Relativitätstheorie nennen,
• sondern auch, wie diese Arbeit (und ganz sicher auch die Tatsache, dass ihr Erfolg beschieden war), Einsteins Verhältnis zur Mathematik geprägt haben:

Aus jemand, der — wie Einstein selbst mehrfach betonte — mit der Mathematik eher auf Kriegsfuß stand, wurde jemand, dessen Erfolg man heute gut dazu benutzen kann, den schärftsten Kritikern der Stringtheorie — Peter Woit und Alexander Unzicker etwa — zu zeigen, wie falsch es wäre, sämtliche Arbeiten an ihr aufzugeben nur deswegen, weil sie sich mit Überlegungen befasst, in die hinein ihr Experimentalphysik nicht mehr folgen kann.

Carrier schreibt (S. 152)

 

Einsteins methodologische Orientierung erfuhr durch die Erfahrung mit der Formulierung der ART eine tiefgreifende Änderung:
 
Die ART sollte die in der SRT enthaltene Gleichberechtigung von Bezugssystemen erweitern und insbesondere Bewegungungen Im Gravitationsfeld einschlie­ßen. {Seine dabei gemachte] Erfahrung der Alternativlosigkeit der mathematischen Konstruktion einer Theorie prägte Einstein tiefgreifend und führte zu einer Abwendung von der operationalistischen Ausrichtung seiner jungen Jahre und zu Zweifeln an der heuristischen Kraft von Beobachtungen.
 
Für Einstein sind es nicht die komplizierte und entlegene Erfahrungsbefunde, wie sie in hochentwickelten Experimenten zutage treten, sondern allgemeine Tatsachen und mathematische Zwangsbedingungen, die die Gestalt der Theorie fixieren:
 

Die ersten und wichtigsten jener Bedingungen, die Einstein sich gesetzt hatte, waren

• das Machsche Prinzip
• das Äquivalenzprinzip und
• das Prinzip allgemeiner Kovarianz (ein rein formal mathematisches)

Carrier schreibt (S. 153)

 
Rückblickend erklärte Einstein: » Noch etwas anderes habe ich aus der Gravitationstheorie gelernt: Keine noch so umfangreiche Sammlung empirischer Fakten kann zur Aufstellung derart verwickelter Gleichungen führen. ...
 
Gleichungen von solcher Komplexität wie die Gleichungen des Gravitationsfeldes können nur dadurch gefunden werden, daß eine logisch einfache mathe­matische Beziehung gefunden wird, welche die Gleichungen völlig oder nahezu determiniert. Hat man aber jene hinreichend starken formalen Bedingungen, so braucht man nur wenig Tatsachenwissen für die Aufstellung der Theorie. « (Einstein 1949, 33; vgl. Howard 2004)
 
 
Bei der Formulierung der ART gewinnt Einstein den Eindruck der  Unausweichlichkeit .
 
Die zentrale Kreativitätsleistung besteht für ihn darin, den angemessenen mathematischen Begriffsapparat zu finden. Ist er richtig gewählt, so führt die Bedingung, die Gleichungen der Theorie sollten möglichst einfach sein, zum  k o r r e k t e n  Ergebnis.
 
Einstein selbst schreibt 1930: » Das eigentlich schöpferische Prinzip liegt in der Mathematik.
 
In einem gewissen Sinne halte ich es also für wahr, daß dem reinen Denken das Erfassen des Wirklichen möglich ist, wie es die Alten geträumt haben. «
 
Der Gegensatz zwischen dem erfahrungs- und praxisorientierten Einstein der frühen Zeit und dem Einstein der späteren Jahre springt ins Auge.
Nach seiner Kehrtwende rückte Einstein die traditionell mit dem Platonismus verknüpfte konstruktive Rolle der Mathematik für die Naturerkenntnis ins Zentrum.
Zwar entscheiden die Tatsachen nachträglich über die Brauchbarkeit einer Theorie, aber für den kreativen, den Fortschritt vorantreibenden Physiker sind Tatsachen im Kern ohne Belang.
 

 
 
Wie also kann man da den Stringtheoretikern noch vorwerfen wollen, ihr Vorhaben sei sinnlos?
 
Vielleicht wird man jetzt verstehen, warum es mich traurig macht, zu lesen, dass Unzicker — übrigens schon im Epilog seines Buches Auf dem Holzweg durchs Universum — Edward Witten und Lisa Randall als "euphorische Märchenerzähler" einstuft. Es passt dies so gar nicht zur Tatsache, dass eben jener Witten auf der Konferenz "Strings 2013, Korea" den seiner Vorträge, der für die Öffentlichkeit gedacht war, mit der Einschätzung schloß (aus meinem Gedächtnis zitiert): Die Stringtheorie steht heute, was Erkenntnisse betrifft, noch ganz am Anfang. Wir wissen noch nicht recht viel mehr, als dass hier etwas sein muss, das untersucht zu werden verdient.
 
Unzicker und Woit — deren erklärte Absicht ja ist, die Ehrlichkeit wissenschaftlicher Argumentation zu verteidigen — müssen sich meiner Meinung nach also wirklich fragen lassen, ob sie in ihrem Eifer nicht genau den Fehler machen, den sie den Stringtheoretikern vorwerfen. Tun die denn nicht genau das, was Einstein über ein ganzes Jahrzehnt hinweg tat,  b e v o r  es ihm gelang, seine Feldgleichungen dann auch wirklich zu formulieren?
 
Und gar noch zu behaupten, Einstein würde sich Grabe umdrehen, wenn er wüsste, was die Stringtheoretiker treiben, ist angesichts seiner eigenen, oben erklärten Kehrtwende doch sicher absoluter Unsinn. Es würde mich freuen, wenn Herr Unzicker (dessen Bücher ich ansonsten schätze) das einsehen oder mir wenigstens hierauf antworten wollte.
 
 
 
Quellen:

• Einstein, Albert (1930): Zur Methodik der Theoretischen Physik, Seite 113-119 in: Einstein (1984): Mein Weltbild, ed. Carl Seelig, Ullstein
   
• Einstein, Albert (1949): Autobiographisches, in: P.A. Schilpp: Albert Einstein als Philosoph und Naturforscher. Eine Auswahl, Braunschweig: Vieweg 1983, 1-35
   
• Howard, Don A. (2004): Einsteins Philosophy of Science, The Stanford Encyclopedia of Philosophy (Spring 2004 Edition), hier online

 

 

 
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als erstes
 
 
Das Machsche Prinzip
 
 
Was Einstein das Machsche Prinzip nannte, bringt zum Ausdruck, dass Einstein — wie vor ihm schon Leibniz und Mach — nicht an die Existenz eines "absoluten" Raumes glaubte, der auch als leerer Raum noch existieren würde, als Behälter also, der durch Objekte bewohnt oder auch nicht bewohnt sein könnte.
 
Newton — der in diesem Punkt ganz anderer Ansicht war als sein Zeitgenosse Leibniz — hatte argumentiert, dass das Auftreten von Trägheitskräften nichts mit Beziehungen zwischen den betroffenen Körpern und anderer Körper zu tun habe, sondern stattdessen die "wahre Bewegung" des Körpers, d.h seine Bewegung relativ zum absoluten Raum widerspiegle.

Martin Carrier (in seinem Buch Raum-Zeit, de Gruyter 2009, S. 138-139)

 
Einstein hielt nichts von diesem Gedanken. Sein zentrales Motiv war die bei Newton angenommene Einseitigkeit der Kausalwirkung, nach der der absolute Raum Trägheitskräfte entstehen lässt ohne dass es Rückwirkung der Körper auf ihn gibt.
 
Einen solch einseitigen Kausaleinfluss hielt Einstein für widersinnig und wollte ihn durch die Vorstellung ersetzen, dass die Trägheitseigenschaften bewegter Körper generell durch ein physikalisches Feld bestimmt sind, ähnlich dem elektromagnetischen Feld.
 
In diesem Denkansatz kann der Raum zwar weiterhin physikalische Wirkung entfalten, jedoch müssen umgekehrt die Körper auch auf ihn Einfluss nehmen können. Für Einstein bedeutet das: Die metrischen und geodätischen Eigenschaften der Raumzeit sollten zur Gänze durch die relativen Lagen und Bewegungen von Körpern (oder anderen Energieformen) festgelegt sein.
 
Er nannte dieses Prinzip das Machsche Prinzip .
 
Es impliziert, dass das Auftreten von Trägheitskräften zur Gänze durch Relativbewegungen festgelegt ist, nicht aber durch Bewegungen der Körper gegen den Raum.
 

 
Obgleich das Machsche Prinzip Einsteins Weg zur ART bahnte, ist es in der voll entwickelten Theorie tatsächlich  n i c h t  erfüllt
 
( wie Carrier in den Abschnitten 4.1.4 und 4.2.2 seines Buches erklärt ):
 
 
Für jede Theorie muß grundsätzlich unterschieden werden

• zwischen der Theorie einerseits und
• den zu ihr konformen Modellen andererseits (die sich ja in durch die Theorie nicht voll bestimmten Eigenschaften durchaus unterscheiden können).

Die ART, als Theorie, ist gegeben durch Einsteins Feldgleichungen. Jedes ihrer Modelle entspricht einer Lösung dieses Gleichungssystems, und obgleich man bisher nur wenige dieser Lösungen kennt, sind darunter neben solchen, die das Machsche Prinzip uneingeschränkt bestätigen, auch solche, in denen es Einschränkun­gen unterliegt.
 
Es gibt demzufolge zwei unterschiedliche philosophische Haltungen:

• Als Relationalismus bezeichnet man einen Standpunkt, der zwar anerkennt, dass die ART Lösungen kennt, die das Machsche Prinzip nicht automatisch erfüllen, der diese Lösungen aber als philosophisch belanglos einstuft, da sie nicht mit den Erfahrungsbedingungen unserer Welt übereinstimmen.
   
  
• Der absolute Ansatz dagegen kennt keine Konzentration auf die faktisch realisierten Lösungen. Seine Anhänger stehen auf dem Standpunkt, dass die ART keinen Rückgriff auf Bezugskörper verlange und keine Rückführung von Trägheitskräften auf Relativbewegungen erzwinge. Die nicht-Machschen Lösungen seien ebenfalls relevant, da sie zur Beschreibung kleinräumiger kosmischer Strukturen (mit ihren lokalen Abweichungen von Homogenität und Isotropie) gebraucht werden.

Festzuhalten ist, dass die ART dem Machschen Prinzip nicht zwangsläufig genügt. Die von Friedmann 1922 gefunden Lösung allerdings — sie gilt bislang als unser bestes Modell des Universums — genügt ihm uneingeschränkt und kommt ohne Randbedingungen aus (etwa solche, die annehmen, dass es irgendwo weit draußen im Universum gar keine Materie mehr gebe, dass das Universum rotiere, oder was da sonst noch denkbar sein mag).
 
Für eine umfassende Beschreibung kosmischer Strukturen aber reicht Friedmans Lösung  n i c h t  aus: Lokalen Abweichungen von der Homogenität — etwa bei Planetensystemen oder Schwarzen Löchern — muss durch Größen Rechnung getragen werden, die absolut sind, bei denen also nicht alle geometrischen Strukturen einfach nur auf die relative Lage der Körper zueinander zurückführbar sind.
 
 

Rüdiger Vaas (in seinem Buch Jenseits von Einsteins Universum, 2016, S. 220-222):

 
Den Begriff das Mach'sche Prinzip hat Einstein 1918 zu Ehren des 1916 verstorbenen Ernst Mach eingeführt. Er steht für Machs Aussage, dass die Trägheit eines Körpers bestimmt sei durch den Einfluss, den alle sonst noch im All vorhandenen Körper auf ihn haben.
 
In Einsteins Theorie ausgedrückt:
 
Der durch den Metriktensor g_μν beschriebene » Raumzustand «
— auch das Gravitationsfeld, welches durch den Energie-Impuls-Tensor T_μν bedingt wird —
sei  r e s t l o s  durch die Massen der Körper bestimmt.
 
Einstein bedauerte, dieses Prinzip zunächst nicht klar genug vom Relativitätsprinzip unterschieden zu haben, das er nun so definierte:
 
 
» Die Naturgesetze sind nur Aussagen über zeiträumliche Koinzidenzen.
 
Sie finden  d e s h a l b  ihren einzig natürlichen Ausdruck in allgemein kovarianten Gleichungen. «
 
 
Einstein räumte ein, das Mach'sche Prinzip würde » keineswegs von allen Fachgenossen geteilt «, er selbst aber empfinde » seine Erfüllung als unbedingt notwendig «.
 
Ob Einstein berechtigt war, sich auf Mach zu beziehen, erscheint fraglich (und wird von Wissenschaftsphilosophen wie etwa John Norton mit guten Gründen bezweifelt): Mach selbst hatte wohl keine klare Konzeption von dem, was Einstein nach seinem Tode das Mach'sche Prinzip nannte.
 
Mittlerweile gibt es mindestens 20 Formulierungen, keine deckungsgleich mit einer anderen, und manche sind ziemlich sicher falsch ...
 

Klaus Kiefer (auf S. 60 in Quantenkosmos):

 
Einstein verstand das Machsche Prinzip ursprünglich so, dass die Geometrie der Raumzeit — ihre Metrik — durch die Materieverteilung eindeutig bestimmt sein sollte. Wie Einstein selbst aber nachträglich feststellen musste, ist das in der ART nun aber doch nicht der Fall: Die Metrik geht in alle bekannten Materiegleichungen ein und kann daher nicht durch die Materie bestimmt sein.
 
Zudem sind es ja gerade die lokalen Gravitationsfelder, welche für das lokale Trägheitsverhalten am dominantesten bestimmen (und nicht — wie noch Mach meinte — die fernen Fixsterne bzw. alle Körper im Raum gleichermaßen).
 

Noch 1917 hat Willem de Sitter Einstein darauf aufmerksam gemacht, dass seine Feldgleichungen auch absolut leere, unendlich weite Raumzeiten zulassen (und die noch nicht mal statisch sein müssen). Wegen der hier angenommenen kosmologischen Konstanten zieht sich die Raumzeit zunächst zusammen, expandiert dann aber wieder (was aber beides erst später klar wurde). Diese Beispiele zeigen, dass die Metrik doch nicht — wie Einstein dachte — allein durch den Energie-Impuls-Tensor bestimmt ist.
 
Ausgehend hiervon sah Einstein schließlich auch ein, dass seine Theorie gar nicht auf der Relativität der trägen Masse aufbaut oder sie erfordert, sondern lediglich auf der Relativität der Bezugssysteme. In einem Brief aus 1954 schrieb er dann schließlich, dass man vom Mach'schen Prinzip überhaupt nicht mehr sprechen sollte.
 
Damit ist nun aber erneut die Frage berechtigt, ob die Natur nicht vielleicht doch auch absolut leere Raumzeit kennt.

 

 

 
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als zweites
 
 
Das schwache und das starke Äquivalenzprinzip
 
 
Unter dem  s c h w a c h e n  Äquivalenprinzip versteht man die Gleichheit von schwerer und träger Masse:

Einstein (1922)

 
Die bisherige Mechanik hat diesen wichtigen Sachverhalt zwar registriert, aber nicht interpretiert.
 
Eine befriedigende Interpretation kann nur so zustandekommen, dass man einsieht: Dieselbe Qualität des Körpers äußerst sich je nach Umständen als Trägheit oder als Schwere.
 

Danach stellen schwere und träge Masse lediglich unterschiedliche Manifestationen einer einzigen Grundgröße dar.
 
 
Nach dem schwachen Äquivalenzprinzip lässt sich gleichförmige Beschleunigung im feldfreien Raum nicht von geradlinig-gleichförmiger Bewegung im einem gleichförmigen Gravitationsfeld unterscheiden.

 
Der Schluss ist, dass gleichförmige Beschleunigungen und homogene Gravitationsfelder für alle mechanischen Prozesse empirisch äquivalent sind.
 
Die Annahme, dass dies nicht allein für mechanische Prozesse, sondern sogar für  s ä m t l i c h e  physikalischen Vorgänge gelte, wird als  s t a r k e s  Äquivalenzprinzip bezeichnet. Erst Einstein sprach davon.

 
Verknüpft mit Machschen Prinzip führt das starke Äquivalenzprinzip auf ein Charakteristikum der ART, welches darin besteht, den absoluten Raum zu vermeiden.
 
WICHTIG aber:

Das Äquivalenzprinzip lässt sich nur auf  h o m o g e n e  Gravitationsfelder anwenden. Seine Erweiterung auf inhomogene Felder — solche mit räumlich oder zeitlich wechselnder Feldintensität — verlangt eine bloß lokale Anwendung auf räumlich und zeitlich benachbarte Ereignisse.

Gutes Beispiel eines inhomogenen Gravitationsfeldes ist das kugelsymmetrische Feld der Erde. In ihm ist die Schwerebeschleunigung auf den Erdmittelpunkt gerichtet und weist daher an unterschiedlichen Orten in meist unterschiedliche Richtung. Folglich ist das Schwerefeld der Erde  n i c h t  durch Übergang in ein einziges beschleunigtes Bezugssystem im feldfreien Raum nachzubilden. Nur wer sich auf einen hinreichend kleinen Bereich des irdischen Schwerefeldes beschränkt, kann für ihn ein Bezugssystem derart wählen, dass das Schwerefeld verschwindet (niemals ganz genau, wohl aber ausreichend genau unter praktischen Gesichtspunkten).
 
Auch die Tatsache, dass ein in einem beliebigen Gravitationsfeld frei fallender Beobachter die Existenz des Feldes grundsätzlich überhaupt nicht nachweisen könne, gilt nur in sehr kleinen Bereichen: Darüber hinaus nämlich wäre — genügend genaues Messgerät vorausgesetzt — die Auswirkungen der Raum-Zeit-Krümmung anhand sog. Gezeitenkräfte erkennbar, d.h. anhand der Deformationen, die sämtliche Körper im inhomogenen Gravitationsfeld erfahren. Wenn z.B. eine verformbare Kugel der Erde entgegen fällt, wirkt die Gravitationskraft am unteren Ende der Kugel stärker als am oberen (da sie ja der Erde schon näher ist), so dass die Kugel sich in Fallrichtung verlängert ind insgesamt elliptische Form annimmt.
 
Dass man diese Kraftdifferenz als Gezeitenkraft bezeichnet, liegt daran, dass die irdischen Wassermassen auf der dem Mond zugewandten Seite von ihm stärker angezogen werden als auf der ihm abgewandten Seite. Deshalb ist das Wasser an beiden Seiten relativ zum Erdzentrum in Richtung des Mondes beschleunigt, was — da der Mond die Erde umkreist — ständigen Wechsel zwischen Ebbe und Flut zur Folge hat.
 
Wirklich exakt also gilt das Äquivalenzprinzip nur in einer ausdehnungslosen Umgebung des Beobachters, die — da ausdehnungslos — nur den Punkt enthält, in dem der Beobachter ruht. Mit zunehmendem Abstand von ihm werden z.B. Gezeitenkräfte immer deutlicher hervortreten. Wirklich zu Null wird das Gravitationsfeld nur im Beobachter selbst: Das  s t a r k e  Äquivalenzprinzip hat nur  l o k a l e  Gültigkeit.

 
Bisher konnten Experimente das Äquivalenzprinzip bis zu einer Genauigkeit von 10^-13 bestätigen. Dennoch ruht man nicht:

 

• Das Äquivalenzprinzip mit noch höherer Genauigkeit nachzuprüfen ist Aufgabe des von der ESA verantworteten Projekts Weltraummission MICROSCOPE.
   
• Um die Jahreswende 2013/2014 wurde ein exotisches 3-Sterne-System entdeckt, mit dessen Hilfe sich die uneingeschränkte Gültigkeit des starken Äquivalenzprinzips mit um einige Größenordnungen höherer Genauigkeit als bisher wird nachprüfen lassen. Siehe Relativitätstheorie im Präzisionstest (Jan 2014).

 
 
Folgen des Äquivalenzprinzips
 
 
Nach dem Äquivalenzprinzip ist es physikalisch nicht unterscheidbar, ob eine in einem System auftretende Kraft sich als Folge von Beschleunigung ergibt oder durch Gravitationsquellen hervorgerufen ist.
 
Mit anderen Worten: Schwerkraft und Trägheitskräfte (wie etwa die Fliehkraft) sind aufsummierbar und können sich daher — als gerichtete Kräfte — auch gegenseitig aufheben.
 
Die Erde umkreisende Raumfahrer etwa machen sich das zunutze: In der typischen Flughöhe von IIS und Mir ist die Schwerkraft nur etwa 15% geringer als auf der Erdoberfläche. Schwerelos sind die Raumfahrer darin nur deswegen, weil

 

• auf sie — da sie sich ja kreisförmig um die Erde bewegen — auch Fliehkraft wirkt
   
• und die Flughöhe ihrer Umlaufbahn so gewählt wurde, dass Fliehkraft und Schwerkraft sich zu Null aufaddieren.
   
• Möglich ist das nur, weil nach dem Äquivalenzprinzip beide Kräfte gleicher Natur sind.

 
 
Historische Notiz:
 
 
Für Newton war Trägheit durch den Raum hervorgerufen, Gravitation aber durch die sich anziehenden Objekte im Raum.
 
Erst Einstein sah beide als Erscheinungsformen ein und derselben Sache: der Geometrie der Raumzeit.
 
 
Daher ist selbst noch die Fliehkraft, der wir während einer Karusselfahrt ausgesetzt sind, ein Aspekt der Gravitation.

 

 

 
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als drittes
 
 
Das Prinzip allgemeiner Kovarianz
 
 
Einsteins Ziel war, seine Theorie so zu formulieren, dass ihre Ausdrücke in allen Bezugssystemen anwendbar sind — nicht allein in Inertialsystemen.
 
Zulässige Transformationen zwischen Bezugssystemen sollten nur eingeschränkt sein durch die Bedingungen

• umkehrbar eindeutig,
• stetig,
• und auch differenzierbar.

Wie bedeutsam das ist, wird klar, wenn man sich vor Augen führt, dass die Gesetze der Newtonschen Mechanik (wie auch der SRT) zunächst nur in Inertialsystemen gültig sind und an nicht-inertiale Bezugssysteme nur durch Einführung zusätzlicher Größen — Zentrifugalkräfte oder Crioliskräfte — anpassbar sind.
 
Solche Sonderstellung einer besonderen Klasse von Bezugssystemen wollte Einstein in der ART vermeiden:
 
Sein Ziel war, die Theorie so zu formulieren, dass ihre Gesetze in unveränderter Form in allen denkbaren Bezugssystemen gültig bleiben.
 
Allgemeine Kovarianz erreicht genau das. Zulässig sind danach nur Größen, die ein ganz bestimmtes Transformationsverhalten aufweisen.Man nennt sie kovariante Größen. Kovarianz ist ein der Differentialgeometrie entstammender, rein mathematischer Begriff. Einstein gelang es, ihm mit physikalischer Relevanz zu versehen. Einstein glaubte 1916, dass das Prinzip allgemeiner Kovarianz als Ausdruck und Konkretisierung eines "allgemeinen Relativitätsgesetzes" gelten könne, demzufolge sämtliche Bewegungsformen physikalisch gleichwertig sind:

Einstein (1922)

 
Wir werden dem Relativitätsprinzip im weitesten Sinne dadurch gerecht, dass wir den Gesetzen eine solche Form geben, daß sie bezüglich jedes derartigen (4-dimensionalen) Koordinatensystems gelten, d.h. daß die sie ausdrückenden Gleichungen bezüglich beliebiger Transformation kovariant sind.
 

Martin Carrier (in seinem Buch Raum-Zeit, de Gruyter 2009, S. 143-144)

 
Allerdings hat das Prinzip allgemeiner Kovarianz nichts mit der Relativität der Bewegung zu tun. Wie Erich Kretschmann 1917 zeigen konnte, beinhaltet die mathematische Tatsache der unveränderten Form der Gleichungen in beliebigen Koordinatensystemen keineswegs auch die physikalische Äquivalenz aller Bezugssysteme.

Allgemeine Kovarianz bingt zum Ausdruck, dass sich die Größen der Theorie und ihre Beziehungen untereinander in koordinaten-unabhängiger Form darstellen lassen, schließt aber  n i c h t  aus, dass bei der Umsetzung der übergreifenden Darstellung in konkrete Bezugssysteme doch wieder spezifische Merkmale besonderer Bewegungsformen in Erscheinung treten.
 
Tatsächlich lässt sich beinahe jede Bewegungstheorie allgemein kovariant formulieren (SRT und Newtonsche Mechanik auf jeden Fall).
 
Dabei konkretisiert sich dann die die einheitliche Formulierung in verschiedenen Bezugssystemen auf unterschiedliche Weise.
 
Insbesondere treten in Nicht-Inertialsystemen unverändert Trägheitskräfte in Erscheinung, so dass sich an der Sonderstellung der Initialsysteme nichts geändert hat.

Um es nochmals zu sagen:

Allgemeine Kovarianz ist eine mathematische Eigenschaft der  F o r m u l i e r u n g  einer Theorie.
Physikalische Äquivalenz von Bezugssystemen aber garantiert sie keineswegs.

Neu in der ART ist allein, dass ein allgemein kovariante Formulierung dort unvermeidlich ist, da die von Punkt zu Punkt unterschiedliche Krümmung der Raumzeit keine globalen Inertialsysteme mehr zulässt (Friedmann 1983, 54-56, 207-209, 212-213).

Quelle:

• Friedmann, Michael (1983): Foundations of Space-Time Theories, Relativistic Physics and Philosphy of Science, Princeton University Press

 

 
Die Formulierung eines physikalischen Gesetzes heißt  k o v a r i a n t , wenn sie koordinatensystem-unabhängig ist.

 

 

 
Wie es zur Stringtheorie kam
 
 
Als Geburtsjahr der Stringtheorie gilt 1968:

• Damals nämlich war zwei am CERN forschenden, jungen Physikern — unabhängig voneinander — aufgefallen, dass die sog. Eulersche Beta-Funktion (von Euler schon im 19. Jahrhundert entwickelt) erstaunlich gut geeignet war, das Verhalten stark miteinander wechselwirkender Teilchen zu beschreiben (sprich: den Austausch von Bosonen, die als Träger der sog. Starken Kernkraft gelten).
   
• Die durch die beiden Entdecker dieser Tatsache gefundene Formel machte aber auch einige unzutreffende Aussagen. Doch schon 1969 konnten drei andere Physiker dieses Problem beseitigen, indem sie die Formel um kleine Zusatzterme ergänzt hatten.
   
• Noch ein Jahr später — 1970 — legte dann der japanische Physiker Y. Nambu, aufbauend auf dieser Formel, endgültig den Grundstein der Stringtheorie: Sein Forschungsgebiet waren Symmetrien, ihre tiefer Bedeutung und die Art und Weise, in der man sie immer wieder gebrochen vorfindet. Nambus Idee war, die punkteförmigen Teilchen des Standardmodells der Elementarteilchenphysik durch 1-dimentionale schwingende Gebilde zu ersetzen, die an die Saiten eines Musikinstruments erinnern (engl. Strings) und genau ein Plancklänge lang sind.
  
  Die so erhaltene Stringtheorie — die sog bosonische — kannte geschlossene und offene Strings, konnte aber nur Bosonen (nicht auch Fermionen) modellieren. Sie war 26-dimensional, was viele Anomalien (in den Prozessen der Teilchenumwandlung) und Unendlichkeiten zur Folge hatte.

 
In dieser Form allerdings hatte die Stringtheorie noch ganz gravierende Mängel:

• Sie war weder zur Relativitätstheorie noch zu allen quantenmechanischen Erkenntnissen konform.
• Sie sagte auch Tachionen voraus (d.h. überlicht-schnelle Teilchen).
• Zudem hätte unsere Welt nach dieser Variante der Stringtheorie 26 Dimensionen haben müssen.

Vor allem dieser Gründe wegen, dachten damals viele Physiker, der Ansatz sei eine Sackgasse.
 
Erst als Michael Green und John Schwarz — die Väter der sog. Superstringtheorie — sich auf eine supersymmetrische Variante der Stringtheorie konzentrierten, war eine Version gefunden, die

• mit 10 Raumdimensionen auskam
• und sämtliche Symmetrien beschrieb, die das Standardmodell der Elementarteilchenphysik im Verhalten der Bosinen und Fermionen kennt.

Diese Variante der Stringtheorie (Typ I) stütze sich auf offene und auch auf geschlossene Strings. Schon 1 Jahr später — 1985 — präsentierten Green und Schwarz eine zweite Variante (genannt Typ II), welche nur noch geschlossene Strings betrachtete.
 
Sie war frei von Tachionen und enthielt ein masseloses Teilchen mit Spin 2, das sog. Graviton (dessen Existenz die Schöpfer des Standardmodells zwar immer vermutet, aber nie hatten modellieren können).
 
Damit konnte man nun tatsächlich viele Physiker davon überzeugen, dass diese supersymmetrische Form der Stringtheorie ein guter Weg sein könnte hin zu einer Theorie, welche das Verhalten sämtliche Fermionen, sämtlicher Bosonen, und auch des Gravitons derart treffend beschreibt, dass sie als Vereinigung von Quantenmechanik, dem Standardmodell und der Allgemeinen Relativitätstheorie in Frage kommen könnte.
 
 
Dennoch schien sich diese Hoffnung zunächst nicht zu erfüllen:

• Haupthindernis war die Tatsache, dass Strings nicht punktförmig sind, sondern Ausdehnung haben.

Doch bald fand man einen Weg, die Strings auch als punktförmig anzusehen: dann jedenfalls, wenn man sich auf große Abstände konzentrierte (und so ein relativ niedriges Energieniveau annehmen konnte). Die erzielten Erfolge waren groß genug, dass Begeisterung aufkam:
 
 
 
Man sprach jetzt von der Superstring-Revolution und sah die Weltformel in greifbare Nähe gerückt.
 
Zudem war jetzt klar geworden, dass man nicht nur Strings zu betrachten hatte, sondern auch höher-dimensionele schwingende, membranartige Gebilde (sog. Branen).
 
Berechnet man nun aber mit Hilfe der Stringgleichungen, wie sich Strings teilen und vereinigen, so musste man feststellen, dass da laufend Anomalien und Unendlichkeiten auftraten, die die Theorie entwerteten. Erstaunlicherweise aber traten die immer nur in Verbindung mit dem Faktor (η-10) auf, wo η die Zahl der angenommenen Dimensionen bezeichnet. Da dieser Faktor für η = 10 zu null wird (und die Probleme dadurch verschwinden), dachte man dann, dass alle durch die Stringtheorie sinnvoll beschriebenen Welten 9 Raum- und 1 Zeitdimension hätten.
 
 
Ernüchterung trat ein, als man dann während weniger Jahre noch 3 weiter Varianten der Stringtheorie fand (alle basierend auf nur geschlossenen Strings). Damit waren 1995 immerhin 5 verschiedene Stringtheorien bekannt:

• Eine Variante (genannt Typ I) betrachtete offene und geschlossene Strings.
   
• Vier weitere Varianten (genannt Typ IIA, Typ IIB, o-heterotisch, und E-heterotisch) betrachteten nur geschlossene Strings.

Die Angst, dass es noch mehr Varianten geben könnte, wuchs ...
 
 
 
Dann aber kam es — 1995 — zur sog. Zweiten Superstring-Revolution:
 
Mit Hilfe sog. Dualitätsprinzipien (wonach scheinbar unterschiedliche physikalische Prinzipien dennoch ein und dasselbe Verhalten der Natur beschreiben) konnte Eduard Witten zeigen, dass

• die bis dahin gefundenen fünf 10-dimensionalen Varianten der Stringtheorie
• sowie eine damals auch schon konstruierte 11-dimensionale, supersymmetrische Quantenfeldtheorie

sämtlich Grenzfälle einer umfassenderen 11-dimensionalen supersymmetrischen Theorie sind (die er M-Theorie nannte).
 
 
In [1] liest man: M-theory contains extended objects of a whole slew of different spatial dimensions called p-brane (an object with p space dimensions, up to nine). It seems the fundamental ingredients in the M-theory are "branes" of a variety of dimensions.
 
Daraus folgt:
 
 
Der M-Theorie nach könnte unsere Welt eine dieser p-Branen sein,
 
d.h. bis zu 10 räumliche Dimensionen haben ( 6 davon bisher nie beobachtet ).
 
 
Note: Wer über die bisher experimentell nicht nachweisbaren 6 Dimensionen spricht, geht davon aus, dass es sich dabei um kompaktifizierte ( zusammengerollte )
r ä u m l i c h e  Dimensionen handeln müsse. Mir aber scheint das nicht zwingend zu sein, denn schließlich stellen Dimensionen einer Theorie ja genau genommen nur unabhängig voneinander variierbare Freiheitsgrade dar. FRAGE also:
 
 
Könnte es sein, dass die 6 zusätzlichen, der Experimentalphysik unbekannten Dimensionen
 
weder räumlicher noch zeitlicher Natur sind?
 
 
Heute wird oft der Eindruck erweckt, die Stringtheorie trete auf der Stelle. Die Stringtheoretiker aber sind optimistisch: Sie sind fest davon überzeugt, dass wir nur noch nicht die richtigen mathematischen Werkzeuge haben, in der Stringtheorie schlummernde Aussagen zu entschlüsseln. Sie könnten recht haben, denn dass die siebte verborgene Dimension erst so spät entdeckt wurde, hängt damit zusammen, dass die Gleichungen der Stringtheorie über Jahrzehnte hinweg nicht genau genug gelöst werden konnten [ so schreibt Karamanolis in seinem Buch » Die Suche nach der Weltformel « (2006) ].
 
Jetzt also scheinen die Mathematiker am Zuge zu sein ...

 

 

 
Wo steht Stringtheorie heute?
 

Leonard Susskind ( auf S. 410 seines Buches Der Krieg um das Schwarze Loch, 2010 ):

 
Die Stringtheorie wurde durch Zufall entdeckt, und ihre Entwicklung vollzog sich fragmentarisch.
 
Man hat noch keinen umfassenden Satz von Prinzipien, ja noch nicht mal einen kleinen Satz sie definierender Gleichungen.
 
Ähnlich rund wie die Theorien von Newton und Einstein ist sie deswegen noch lange nicht.
 
Bis heute ist sie kaum mehr als ein Geflecht zufällig entdeckter mathematischer Tatsachen, die untereinander bemerkenswerte Konsistenz aufweisen, aber ins­gesamt doch erst eine Menge von Puzzleteilchen sind, von der man noch nicht weiß, wie vollständig sie ist. Ein sich abzeichnenden Gesamtbild zu erkennen ist noch immer schwierig.
 
Dennoch ist Stringtheorie unser bislang bester mathematischer Führer hin zu den Fundamenten einer Theorie, welche sämtliche vier Grundkräfte der Physik gleichermaßen berücksichtigt.
 
Der niederländische Nobelpreisträger Gerard 't Hooft vergleicht den heutigen Zustand der Stringtheorie mit einem Stuhl, dem noch Beine und Sitzfläche fehlen, dessen Armlehnen demnächst aber wohl lieferbar sein werden.
 

Peter Woit ( zitiert durch v. Buttlar auf S. 164 seines Buches RaumZeit, 2009 ):

 
Als die Stringtheorie aufkam, schien sie mir eine spekulative Idee zu sein, die es durchaus wert war, weiter verfolgt zu werden.
 
Doch dann vergingen die Jahre, und mit der Zeit wurde immer klarer, dass Stringtheorie nicht funktioniert.
 
Dennoch erhielten die Strings immer mehr Aufmerksamkeit, und mehr und mehr Leute fingen an, auf dem Gebiet zu arbeiten — obwohl Erfolge ausblieben. In den letzten Jahren ist es sogar noch schlimmer geworden. Mittlerweile ist mir nicht einmal mehr klar, ob das, was die Leute da betreiben, überhaupt noch Wissenschaft ist.
 

 
Ich, Gebhard Greiter, würde es eher so sehen:
 
Die Stringtheorie ist noch zu wenig ausgearbeitet, zu wenig präzisiert, um sie ernsthaft anfechten zu können.
 
Da die der Stringtheorie zugrundeliegende Mathematik extrem schwierig ist, gibt es viele Physiker, die diese Theorie schon allein deshalb nicht bewerten können, weil sie viel zu wenig davon verstehen. Wo sie Kritik an ihr üben, kann man die deswegen auch nicht so recht ernst nehmen.
 
 
Wir müssen berücksichtigen:
 
Stringtheorie beschreibt, was irgendwo in den Tiefen des Weltalls möglich sein sein könnte, also nicht nur die Verhältnisse in "unserem" Universum, d.h. in der doch eher nur "kleinen" Umgebung unserer Erde, die durch unseren Beobachtungshorizont begrenzt ist und einen kegelförmigen Bereich der Raumzeit darstellt, in dem wir maximal 46 Mrd. Lichtahre weit und nur knapp 13,5 Mrd. Jahre in die Vergangenheit sehen können — verglichen mit der Weite des Universums dahinter könnten das extrem kleine, kaum nennenswerte räumliche und zeitliche Entfernungen sein.
 
Man bedenke: Wer sich in Norddeutschland befindet, stets nur dort gewohnt hat und soweit das Auge reicht, nur flaches Land sieht, kann sich ja auch nur schwer vorstellen, dass es auch sehr gebirgige Landschaften gibt. Ähnliches gilt im Kosmos: Astronomen können sozusagen nur unsere "nächste" Umgebung einsehen. Stringtheorie aber erhebt den Anspruch, auch noch zu beschreiben, was erst weit hinter unserem Beobachtungshorizont vorzufinden sein könnte.

 

 

 
Was für Stringtheorie spricht
 
 
Hier einige Argumente, die zeigen, dass es Sinn macht, die Stringtheorie weiter zu erforschen:

 
• Dass Experimentalphysik keine Wege kennt, Ergebnisse der Stringtheorie zu falsifizieren, scheint nicht mehr richtig zu sein: Siehe etwa A first chance to test String Theory (2014).
   
• Per Stringtheorie gelang es erstmals, die thermodynamische Entropie eines Schwarzen Lochs auf mikroskopische Weise zu berechnen: einfach durch Abzählen der ihm möglichen Quantenzustände. Diese Rechnung reproduzierte exakt die Formel von Bekenstein und Hawking, welche den Zusammenhang zwischen der Entropie des Lochs und der Größe der Fläche seines Ereignishorizonts beschreibt.
   
  Quelle: Dieter Lüst: Quantenfische, DTV 2014, S. 244
   
• Stringtheorie ist die erste Theorie, welche die Gravitationskraft als zwingend gegebenen und zudem noch als quantisiert postuliert: Geschlossene Strings führen zwangsläufig auf die Gravitationskraft.
   
  Quelle: Dieter Lüst: Quantenfische, DTV 2014, S. 257
   
• Weitere Erkenntnisse, die erst die Stringtheorie gebracht haben soll, nennt Wikipedia: Wertung der Stringtheorie.

 
 
Wer nicht selbst Stringtheoretiker ist, der sollte solchen Erfolgsmeldungen allerdings auch ein wenig skeptisch gegenüber stehen, da sie meist — bei genauerem Hinsehen — mit Einschränkungen versehen sind (die oft verschwiegen werden). Hier ein Beispiel:

von Baeyer schreibt

 
1996 fanden Stringtheoretiker eine Herleitung der Bekensteinschen Formel aus statistischen Überlegungen: Sie ermittelten die Anzahl der Möglichkeiten, mit denen sich ein bestimmtes » mathematisches Objekt « in ihrer Theorie ungestraft umordnen lässt und sahen, dass der Logarithmus dieser Zahl gerade der Entropie von Bekenstein entspricht.
 
Vorsicht aber: Obgleich das von ihnen untersuchte Modell viele Eigenschaften eines Schwarzen Lochs hat, besitzt es leider nicht all seine Eigenschaften. Insbesondere ist dieses Modell bei Null Grad Kelvin eingefroren und beschreibt daher mit Sicherheit kein echtes Schwarzes Loch mit seiner Hawking-Strahlung.
 
Seither werden im Rahmen der Stringtheorie kompliziertere Modelle untersucht, sog. Gedanken Black Holes . Die Erfolge ermutigen, doch Bekenstein warnt zur Vorsicht: Wenn Sie einen Penny verloren haben und jemand anders findet einen, dann muss das nicht notwendig derselbe sein.
 

 
Klar gesagt werden muss aber auch:

Zum gegenwärtigen Zeitpunkt (2015) ist die Stringtheorie noch keine abgeschlossene, voll akzeptierte physikalische Theorie.
Selbst eine über die Störungstheorie hinausgehende Formulierung ist noch nicht erarbeitet.
 
Ihre Calabi-Yau-Räume implizieren neue Feldkräfte, die erst nachzuweisen wären.

 

 

Stringtheorie kann – wenigstens in Teilen – falsifizierbar sein

Stringtheoretiker werden oft kritisiert mit dem Argument, ihre Theorie sei nicht falsifizierbar.
Wie folgendes Beispiel (schon aus 2004) zeigt, ist diese Kritik aber keineswegs immer berechtigt:

Der extrem helle Gammastrahlenausbruch GRB 041219A in einer Entfernung von rund 300 Millionen Lichtjahren erlaubt Untersuchung energieabhängiger Rotation der Polarisationsrichtung jener Gammastrahlung. In 2004 gelang es, die Genauigkeit der Beobachtung um etwa den Faktor 10.000 zu steigern und so Daten zu bekommen,
mit denen sich in 2011 Details einiger Varianten der Stringtheorie widerlegen ließen.

Der entsprechende Bericht auf pro-physik.de sagt:

Zitat:

 
Die vorliegende Messung ist 10.000-fach genauer, als bei früheren Beobachtungen.

Daraus ergibt sich der unvorstellbar kleine Wert von 10^-48 Meter als Obergrenze für die Größe der Raumzeit-Körnung. Bisher gingen die Forscher davon aus, sie läge im Bereich der Planck-Skala: 10^-35 Meter.

Dieser geringe Wert schließe einige Varianten von Stringtheorie und der Schleifenquantengravitation aus, mit denen die Theoretiker eine Vereinigung von Relativitäts- und Quantentheorie erzielen wollen.
 

 

 

 
Die Raumzeit der Stringtheorie
 
 
Stringtheorie gilt als derzeit aussichtsreichster Kandidat für eine Theorie, die wirklich alle 4 Grundkräfte der Natur berücksichtigt und deswegen Einsteins Gravitationstheorie, die Quantenelektrodynamik und das Standardmodell der Elementarteilchenphysik zu einer einzigen, in sich widerspruchslosen Theorie verallgemeinert.
 
Der mathematische Mechanismus, auf dem sie beruht, legt nahe,
 
dass ihre Gegenstände in einer Raumzeit leben, die nicht nur 3, sogar sogar 9 räumliche Dimensionen hat.
 
Es gibt zwei Möglichkeiten, die Existenz jener Zusatzdimensionen erklärbar zu machen:

 
• Entweder könnten 6 der Raumdimensionen zusammengerollt sein (im Sinne der Kaluza-Klein-Theorie, über die Einstein bis zu seinem Tode ohne Erfolg immer wieder nachgedacht hat).
   
• Es könnte aber auch so sein, dass die Raumzeit, in der wir leben, einen echten  T e i l r a u m  der Raumzeit der Stringtheorie darstellt: eben einen mit weniger Dimensionen.
   
• Selbst eine Mischung beider Möglichkeiten wäre denkbar.

 
Gegen die zweite Alternative spricht, dass alle bisher durchgeführten Messungen beweisen, dass die Kraft der Gravitation — mindestens bis hinunter auf Abstände von 1/10 mm — proportional zum Quadrat des Abstandes beider Massen ist.
 
 
Bis 1994 hatte man noch ein zusätzliches Problem: Man kannte 5 verschiedene Varianten der Stringtheorie — und hatte keine Hinweise darauf, welche besser als die jeweils anderen zur Physik unserer Welt passen könnte. 1994 aber platzte eine Bombe:
 
Edward Witten und Paul Townsend fanden Hinweise darauf, dass jede dieser 5 Theorien (und zudem noch ein weitere, von Witten bei dieser Gelegenheit entdeckte) einfach nur recht eingeschränkte Sichten auf eine allgemeinere Theorie waren, die der Raumzeit statt 10 sogar 11 Dimensionen zuerkennt.

Michio Kaku (2008):

 
Um sich das besser vorstellen zu können, denken Sie an einen Wasserball, um dessen Äquator ein Gummiband gelegt ist. Nehmen Sie nun eine Schere und schneiden Sie den Ball zweimal dem Gummiband entlang durch, so dass seine obere und seine unter Halbkugel abgetrennt werden und nur der vom Gummiband überdeckte Teil bleibt — der entspricht dann einem String im Sinne einer der vorher bekannten Varianten der Stringtheorie.
 
Die 11-te Dimension übrigens bescherte uns zudem noch die Einsicht, dass es nicht nur 1-dimensionale Strings, sondern daneben auch mehrdimensionale gibt (sog. Branen) und dass unser Universum gut einer der mindestens (3+1)-dimensionalen Branen entsprechen könnte.
 
Es müssten dann gar nicht alle der zusätzlichen Dimensionen der stringtheoretischen Raumzeit in sich zusammengerollt (also endlich) sein).
 

Die so gefundene Verallgemeinerung aller 5 Stringtheorien bekam den Namen M-Theorie.
 
Wie die Stringtheoretiker sagen, finden sich sämtliche Elementarteilchen dort wieder als die Schwingungszustände der Strings und Branen.
 
 
Ab etwa 10^-13s nach dem Urknall sind moderne Teilchenbeschleuniger in der Lage, die Situation des frühen Universums zu simulieren. Man weiß daher genau, welche Teilchen ab da auftraten, nämlich alle Teilchen des Standardmodells. So früh allerdings existierten noch keine Verbindungen zwischen Quarks, da die Temperatur des Alls (und damit die Energie der Teilchen) noch zu hoch war.

 

 

 
Was ist ein String im Sinne der Stringtheorie?
 
 
Jeder String im Sinne der Stringtheorie (genauer: der M-Theorie) ist eine Menge von Schwingungen eines p-dimensionalen Kraftfeldes, 1 ≤ p ≤ 9, das zeitabhängige Lage und Form hat. Kurz:
 
 
Ein p-String ist ein in p Dimensionen schwingendes, sich durch die Zeit bewegendes Kraftfeld.
 
 
Im Falle 2 ≤ p nennt man solche Strings dann auch Branen (man denke an schwingende Membranen, wobei die Brane, der String also, aber kein schwingendes Material ist, sondern rein nur die Summe der möglichen Schwingungsmuster eines ihm zugeordneten zeitabhängigen Kraftfeldes im 9-dimensionalen Raum, d.h. der 10-dimensionalen Raumzeit der M-Theorie oder der Superstringtheorie.
 
Ganz so wie z.B. Wellen in einem Teich sich überlagern können (man spricht dann von Wellenpaketen), können auch Strings — als Summe von Wellen bestimmter Wellenlängen im Kraftfeld, das man das Vakuum nennt — einander überlagern:
 
 
 

 
Wie Strings einander durchdringen können
 
Quelle: Universe Review
 
 
 
 
Im Vakuum enstehen solch schwingende Kraftfelder spontan (jedenfalls soweit Physiker das erkennen können).
 
Da Strings — als Fäden oder Membranen betrachtet — offenbar endliche Ausdehnung haben, können sie nicht Wellen jeder beliebigen Wellenlänge enthalten (ganz so, wie man das ja auch von den Saiten eines Musikinstruments her kennt). Nochmals aber: Bei einer Saite oder einer Membran schwingt das Material, aus dem sie besteht, Strings aber kennen nichts, was diesem Material entspräche. Was da schwingt ist eine durch Feldgleichungen definierte Linie oder Fläche, und das Feld, um das es dabei geht, ist ein Feld von Kräften.
 
 
Nebenbei: Im Prinzip gibt es Stringtheorien mit beliebig vielen Dimensionen. Wie sich aber herausgestellt hat, sind solche Theorien nur dann renormierbar, wenn die ihnen zugrundeliegende Raumzeit 10 oder 26 Dimensionen hat (die Zeit jeweils eine davon).
 
Heute (2015) betrachten die Stringtheoretiker vor allem supersymmetrische 10-dimensionale Varianten der Stringtheorie.

 

 

 
Stringtheorie:

Warum und mit welchen Schwierigkeiten
 
 
Was Stringtheorie so interessant macht, ist die Tatsache, dass sie

 

• uns die Existenz von Gravitonen nahelegt (Bosonen, welche Träger der Gravitationskraft sind — der Kraft also, der bis heute weder die Quantenphysik noch das Standardmodell der Elementarteilchen in irgend einer Weise Rechnung trägt.
   
• Angesichts der mehr als 20 vom Standardmodell benötigten, aber nicht erklärten Konstanten, macht es Hoffnung, dass die Stringtheorie gar keine "vom Himmel fallende" Naturkonstanten benötigt: Jedes Herumbasteln an der Theorie erübrigt sich:
   
  Wir können lediglich ihren mathematischen Aufbau erschließen und prüfen, ob er die reale Welt treffender modelliert als alle bisher bekannten Theorien.

Leider ist die Mathematik der Stringtheorie überaus kompliziert: Noch heute — nachdem nun schon 25 Jahre lang Hunderte begabter Physiker und Mathematiker damit gerungen haben —, sind wir weit davon entfernt, die Theorie bis ins Letzte verstanden zu haben oder auch nur kurz und übersichtlich aufschreiben zu können.
 
Forschungsarbeiten haben eine mathematische Struktur von ganz unerwartetem Reichtum zutage gefördert. Physiker nehmen dies als Hinweis, dass sie sich wahrscheinlich auf dem richtige Weg befinden:

 

• Der Gedanke, sämtliche Elementarteilchen könnten Schwingungszustände von Strings sein, kam 1970 Holger Nielsen und Leonard Susskind.
   
• Dass einer dieser Zustände sogar Gravitonen modelliert, entdeckten 1974 John Schwarz und Joel Scherk.
   
• Zusammen mit Michal Green hat Schwarz dann — abseits aller anderen Physiker — rund 10 Jahre zur Klärung einiger mathematischer Feinheiten benötigt.
   
• Erst dann wurde die Stringtheorie so populär, dass sich über Jahre hinweg Hunderte von Physikern damit beschäftigt haben.
   
• Nachdem sie 1998 schon fast aufgeben wollten, konnte Edward Witten zeigen, dass die bis dahin entstanden 5 Varianten der Stringtheorie Grenzfälle einer einzigen Theorie — sog. M-Theorie — sind.
   
• Seitdem allerdings, hat sich trotz zunächst großer Euphorie kein weiterer Fortschritt ergeben.

 
Wissen sollte man auch:

 

• Trotzdem die Stringtheorie — als Theorie — nur einen einzigen Parameter hat (die sog. Kopplungskonstante), hat jede ihrer Lösungen sehr viele Parameter. Sie alle zu berücksichtigen führt in jeder Lösungen auf mehrere hundert von einander unabhängige Freiheitsgrade.
   
• Nach grober Schätzung modellieren all diese Lösungen mindestens 10⁵⁰⁰ Vakua.
   
• Bousso und Polchinski verknüpften diese Vielfalt möglicher Welten mit den Ideen der Theorie ewiger Inflation und kamen so zum Schluss, dass sich innerhalb des inflationär expandierenden falschen Vakuums Blasen bilden, in denen die Energiedichte geringer, die inflationäre Expansion des Raumes also deutlich langsamer ist. In diesen Blasen — so glauben sie — entstehen dann weiter Blasen mit noch niedriger Energiedichte bis hin zu solchen, die in ihrer Qualität unserem Universum zur Zeit des Urknalls entsprechen.
   
  Im Unterschied zu Allgemeinen Relativittätstheorie — nach der die Raumzeit 3+1 Dimensionen hat — hat die Raumzeit der Strinmgtheorie 9+1 Dimensionen, von denen aber 6 kompaktifiziert sind.
   
  Beispiel dazu: Ein Faden scheint aus großer Ferne betrachtet nur eine Dimension zu haben (die ihm Länge gibt). Erst wer genauer hinsieht, bemerkt eine zweite, recht kleine, von Ferne nicht wahrnehmbare Dimension: Sie ist zu einem Kreis aufgerollt (kompaktifiziert, wie die Mathematiker sagen). Sie steht senkrecht auf der nicht kompaktifizierten und macht die Oberfläche des Fadens zu einem beliebig langen Zylinder, dessen Radius der halben Stärke des Fadens entspricht, also endlich (kompakt im topologischen Sinne) ist.
   
  Die unterschiedlichen Charakteristika der etwa 10⁵⁰⁰ durch die Stringtheorie modellierten Welten ergeben sich aus den verschiedenen Möglichkeiten, für 6 der 1+9 Dimensionen der stringtheoretischen Raumzeit Kompaktifizierung zu erreichen.
   
  Hier der Grund, warum es zu derart vielen Möglichkeiten kommt:
   
  Eine einzige Dimension ließe sich nur auf genau eine Art kompaktifizieren: zu einer Ringform (wie beim Faden im Beispiel). Aber schon wenn es etwas 2-Dimensionales zu kompaktifizieren gilt, bestehen mehrere Möglichkeiten: Ergeben können sich eine Kugeloberfläche, eine Torus-Oberfläche oder etwas, das an die Oberfläche aneinander klebender Brezen erinnert. Bei Kompaktifizierung eines Raumes mit drei oder noch mehr Dimensionen steigt die Anzahl möglicher Formen um ein Vielfaches.
   
  Die Eigenschaften stringtheoretisch modellierter Elementarteilchen hängen stark ab von der Art und Weise, in der man sich die 6 zusätzlichen Raum­dimensionen kompaktifiziert denkt.
  
   

 

 
Die wesentlichen Vorzüge der Stringtheorie
 
erklärt durch den Stringtheoretiker Michio Kaku
 
 
Die Stringtheorie hat den entscheidenden Vorteil, dass sie das Wesen der Materie — und auch das der Raumzeit — erklären kann:
 
Sie beantwortet eine ganze Reihe höchst verwirrender Fragen über Elementarteilchen, darunter auch die Frage, warum es so viele gibt.
 
Und tatsächlich: Je mehr wir die Welt der subatomaren Teilchen erforschen, desto mehr finden wir. Bislang sind mehrere hundert bekannt, und die Auflistung all ihrer Eigenschaften füllt Bände.
 
Die Stringtheorie kann ihre Existenz erklären, mehr noch: Sie sagt uns, dass es letztlich unendlich viele gibt, denn sie seien Schwingungsmoden des Strings (sog. Resonanzen):
 
Ein subatomares Teilchen erscheint uns nur deswegen als punktförmig, weil die Strings so extrem klein sind (nur etwa eine Plancklänge groß). Gäbe es aber ein Mikroskop, welches uns erlauben würde, so genau hinzusehen, würden wir das Teilchen als solche Schwingung erkennen. Kurz:
 
Jedes subatomare Teilchen entspricht einer Schwingung des Strings, deren Wellenlänge sie zu einer  R e s o n a n z  macht.
 

Der Begriff der Resonanz ist uns aus dem alltäglichen Leben bekannt. Denken Sie z.B. an das Singen unter der Dusche: Mag unsere Stimme auch noch so unsicher und brüchig sein, in der Abgeschiedenheit unseres Duschraums kann sie klingen wie die eines Opernstars. Es werden nämlich die Schallwellen zwischen den Wänden der Dusche rasch hin und her geworfen, was dazu führt, dass Schwingungen, die leicht in die Abmessungen der Dusche passen, viele Male verstärkt werden und so hallenden Klang hervorrufen. Diese besonderen Schwingungen bezeichnet man als Resonanzen. Sie addieren sich, während alle anderen — deren Wellen falsche Länge haben — sich selbst (durch ihre Reflexionen) aufheben.
 
Oder stellen Sie sich eine Violinsaite vor. Sie kann mit verschiedenen Frequenzen schwingen und dabei musikalische Töne A, B, C usw. hervorbringen. Überleben können nur die Modi, die an den Enpunkten der Saite verschwinden und mit ganzzahliger Häfigkeit zwischen den Endpunkten schwingen.
 
Im Prinzip kann die Saite mit einer unendlichen Zahl verschiedener Frequenzen schwingen.
 
Wir wissen also, dass die Töne, die wir hören, nicht fundamental sind. Der Ton A hat nicht grundsätzlicheren Charakter als der Ton B. Wenn wir verstehen, wie eine Saite schwingt, begreifen wir sofort die Eigenschaften unendlich vieler musikalischer Töne.

Und so ist auch  k e i n e s  der subatomaren Teilchen wirklich fundamental. Als fundamental (nicht weiter teilbar) erscheinen sie uns nur, da unsere Mikroskope nicht stark genug sind, uns ihre Struktur zu zeigen.
 
Tatsächlich sagt uns die Stringtherie, Materie sei nichts weiter als die von diesen schwingenden Strings geschaffenen Harmonien. Und ganz so, wie es eine unendlich viele harmonien gibt, die sich beispielsweise für die Geige komponieren lassen, gibt es auch unendlich viele Materieformen, die sich aus schwingenden Strings konstruieren lassen. Sie alle zu kennen, ist demnach unmöglich.
 
Insbesondere lassen sich die Gesetze der Physik gut vergleichen mit den Harmoniegesetzen, die sich allein aus den Schwingungsmöglichkeiten einer Violinsaite ergeben. So gesehen ist das gesamte Universum — als Menge schwingender Strings — mit einer Symphonie vergleichbar.
 
 
Aber nicht nur die Beschaffenheit subatomarer Teilchen, auch die Beschaffenheit der Raumzeit selbst kann die Stringtheorie erklären:
 
Wenn sich ein String durch die Raumzeit bewegt, tut er das in einer komplizierten Bewegungsfolge, die einer großen Zahl von Konsistenzbedingungen gehorchen muss. Sie sind so zwingend, dass sie die Raumzeit außerordentlich restriktiven Bedingungen unterwerfen. Und so kann der String sich nicht völlig beliebig — wie ein Punkt — durch den Raum bewegen:
 

Er kann sich in kleiner Strings aufteilen oder mit anderen Strings zusammenstoßen und längere Strings bilden. Erstaunlicher Weise aber sind all diese Schleifendiagramme endlich und berechenbar. Dies macht die Stringtheorie zur ersten Quantentheorie der Gravitation in der Geschichte der Physik, die endliche Quantenkorrekturen besitzt.
 
Keine der früher bekannten Theorien — weder Einsteins Gravitationstheorie, noch der Kaluza-Klein-Theorie, und auch nicht der 11-dimensionalen Supergravitationstheorie — kommt diese schöne Eigenschaft zu.

 
Als man die Einschränkungen, die der String der Raumzeit auferlegt, erstmals berechnete, stellt man voller Erstaunen fest, dass sich aus dem String Einsteins Gleichungen ergaben.
 
Das war äußerst bemerkenswert: Ohne eine einzige dieser Gleichungen vorauszusetzen, erlebte man, wie sie sich von selbst aus der Stringtheorie ergaben. Dies zeigt, dass sie nicht fundamental sein können.
 

Kaku schreibt zusammenfassend:

 
Auf diese Weise erhalten wir eine umfassende Theorie sowohl der Materie-Energie als auch der Raumzeit. Und die Einschränkungen sind konsistent und überaus streng:
 
Beispielsweise verbieten sie dem String, sich in 3 oder 4 Dimensionen zu bewegen. Einzig und allein 10 und 26 sind erlaubt. Zum Glück aber bietet die in diesen Dimensionen definierte Stringtheorie genügend Freiheitsgrade, um alle fundamentalen Kräfte zu vereinigen [ alle wirklich gegebenen Symmetrien zu erkennen ].
 
Und so scheint die Stringtheorie vielseitig genug, um alle fundamentalen Naturgesetze zu erklären. Von der einfachen Theorie eines schwingenden Strings ausgehend, kann man neben Einsteins Theorie auch die von Kaluza-Klein, die Supergravitation, das Standardmodell und sogar die GUT ableiten.
 
Man muss es wohl als Wunder bezeichnen, dass man alle Errungenschaften der Physik der letzten 2000 Jahre aus rein geometrischen Argumenten, den möglichen Bewegungen eines Strings, wiedergewinnen kann.
 

 
Quelle: Michio Kaku: Die Physik der unsichtbaren Dimensionen, Rohwohlt 2013, S. 244-248

 

 

 
The Dualities of M-Theory
 

Michio Kaku remembering die 2nd String Revolution:

 
First indications that duality might apply in string theory were found by K. Kikkawa and M. Yamasaki of Osaka Univ. in 1984. They showed that if you "curled up" (compactified) one of the extra dimensions into a circle with radius R, the theory was the same as if we curled up this dimension with radius 1/R.
 
This is now called T-duality: Torus of radius R is equivalent to Torus of radius 1/R.

 
When applied to various superstrings, one could reduce 5 of the string theories down to 3. In 9 dimensions — with one dimension curled up — the Type IIA and IIB strings were identical, as were the E(8) × E(8) and O(32) strings.
 
Unfortunately, T duality was perturbative.

 
The next breakthrough came when it was shown that there was a second class of dualities, called S-duality, which provided a duality between the perturbative and non-perturbative regions of string theory.

 
The existence of S-duality in string theory was first proposed by the Indian physist Ashoke Sen in 1994. One year later Witten saw
that type IIB string theory with the coupling constant g is equivalent — via S-duality — to the same string theory with the coupling constant 1/g.
Similarly, type I string theory with the coupling g is equivalent to the SO(32) heterotic string theory with the coupling constant 1/g.
 
Unlike the T-duality, however, S-duality has not been proven to even a physics level of rigor for any of the aforementioned cases. It remains — strictly speaking — a conjecture, although most string theorists believe in its validity. (Wikipedia)

 
Another duality, called U-duality, is even more powerful: The U-duality group of a given string theory is a group which comprises T- and S-duality and embeds them into a generally larger group with new symmetry generators.

 
The main example is the system type IIA/IIB in d ≤ 8 on T^10-d (T for Torus).
 
These two 10-dimensional theories are different limits of a single space of compactified theories, which are called the moduli space of type II theory (meaning all compactifcations of type IIA and IIB).

 
Then Nathan Seiberg and Witten showed how another form of duality could solve for the non-perturbative region in four dimensional supersymmetric theories.
 
What finally convinced many physicists of the power of this technique was the work of Paul Townsend and Edward Witten: They caught everyone by surprise by showing a duality between 10-dim Type IIa strings and 11-dim supergravity! The non-perturbative region of Type IIa strings, which was previously a forbidden region, was revealed to be governed by 11-dim supergravity theory, with one dimension curled up.

 
At this point, I remember, many physicists — myself included — were rubbing our eyes, not believing what we were seeing.
I remember saying to myself, "But that’s impossible!"

 
All of a sudden, we realized that perhaps the real "home" of string theory was not 10 dimensions, but possibly 11, and that the theory wasn’t fundamentally a string theory at all! This revived tremendous interest in 11 dimensional theories and p-branes. Lurking in the 11th dimension was an entirely new theory which could reduce down to 11-dim supergravity as well as 10-dim string theory and p-brane theory.
 
Vafa added a strange twist to this when he introduced yet another mega-theory, this time a 12-dimensional geometric, non-perturbative version of stringtheory called F-theory (F for "father") which explains the self-duality of the IIB string. Though F-theory is formally a 12-dimensional theory, the only way to obtain an acceptable background is to compactify it on a two-torus. By doing so, one obtains type IIB superstring theory in 10 dimensions.
 
So, will the final theory have 10, 11, or 12 dimensions?
 
Schwarz feels that the final version of M-theory may not even have any fixed number of dimensions. He feels that the true theory may be independent of any dimensionality of space-time, and that 11 dimensions only emerge once we try to solve it.
 
Townsend seems to agree, saying "the whole notion of dimensionality is an approximate one that only emerges in some semiclassical context".
 
Witten believes

 

• that the underlying degrees of freedom of M-theory are yet to be discovered,
   
• that we are on the right track,
   
• but will need a few more "revolutions" to finally solve the theory. So far (2013) there are no signs yet that the next one will occur very soon.

 
Source: Michio Kaku, see also Dieter Lüst, section 1.3.2
 

 
Kaku says "F-Theorie is rather strange: it has two time coordinates, not one, and actually violates 12 dimensional relativity".
 
This contradicts Wikipedia, where we read "F-theory has metric signature (11,1). It is not a two-time theory of physics".
 
Who is right?

 

 

 
Die Landschaft der Lösungen der M-Theorie
 
 
Jede konkrete Quantenfeldtheorie (QFT) ist definiert sich durch eine Wahl von Feldern und ihnen unterstellter Symmetrien.
 
Ganz anders in der Stringtheorie: Um hier ein bestimmtes physikalisches Modell zu erhalten, wählt man die Art der Strings, die man dem Modell zugrunde legen möchte. Es gibt derzeit nur 5 Alternativen hierfür, und die Dualitäten der M-Theorie zeigen, dass sie sämtlich äquivalent zueinander sind:
 

 
 

 

 
 
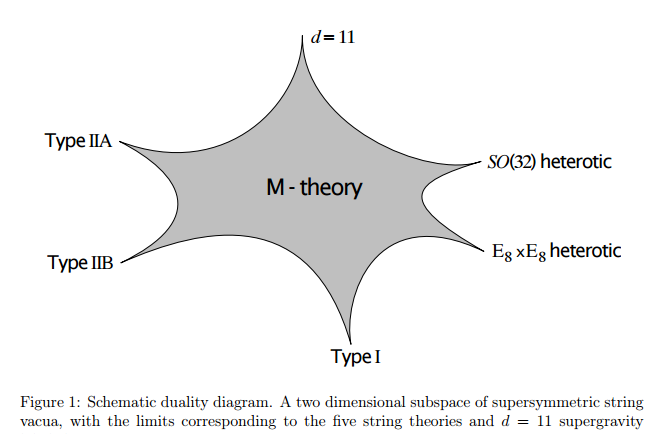
In der Feldtheorie kommt hinzu, dass es zwar unendlich viele Möglichkeiten gibt, die Stärke der Kopplungskonstanten zu wählen, man aber natürlich stets durch die Experimentalphysik erarbeitete, gemessene Werte nehmen wird. Dies passt die QFT ganz automatisch der Welt an, in der wir leben.
 
In der Stringtheorie ist das nicht so einfach: Hier nämlich kommt diese zweite Dimension der Wahlmöglichkeiten aus der Geometrie der versteckten Dimensionen,
und so hat man hier ebenso viele Möglichkeiten, wie es Calabi-Yau-Räume gibt (symbolisch spricht man von etwa 10⁵⁰⁰, aber die genaue Zahl kennt natürlich niemand). Problem dabei: Niemand weiß, welcher dieser Räume denn nun der zu unserer Welt passende ist.
 
 
Quelle: Joseph Polchinski: Dualities of Fields and Strings (2015)

 

 

 
Warum Stringthorie

über ein konkretes Universum so gut wie nichts aussagen kann
 
 
Wie Stringtheoretiker glauben erkannt zu haben, liefert die M-Theorie grob etwa 10⁵⁰⁰ Modelle für möglicherweise existierende Universen [was man wohl so zu verstehen hat, dass man sämtliche Kompaktifizierungen der versteckten Dimensionen als nur eine zählt, die sich – gerundet hin zur Planckskala – im Bereich unseres Universums bzw. irgend einer nur endlich großen Teilregion des gesamten, möglicherweise unendlich weiten Weltalls, nicht mehr unterscheiden].
 
Die Aufgabe, in dieser dann immer noch unglaublich großen Menge von Modellen jenes zu finden, welches unser Heimat-Universum am genauesten beschreibt, erscheint allzu schwierig. Erste Schritte sie zu lösen, sind dennoch schon unternommen. Hier ein Beispiel:
 
Das Standardmodell der Elementarteilchenphysik gruppiert schon beobachtete Elementarteilchen nach 3 Familien. Andererseits haben durch p-Branes dargestellte Elementarteilchen unter­schiedliche Eigenschaf­ten je nachdem welches Modell (der so überaus vielen) man zugrundelegt. Wirklich zu unserem Universum passen können also nur Modelle, die für die Elementarteilchen Eigenschaften postulieren, die denen ent­sprechen, die unsere Experimentalphysik bislang beobachtet hat. Eine dieser Eigenschaften entspricht der Gruppierung nach Familien, und etwas dazu Vergleichbares findet sich auch in den durch die M-Theorie erlaubten Weltmodellen: Die Form nämlich, die jedes solche Modell den im Quantenschaum auftre­ten­den Flächen zuordnet, bestimmt wesentlich die Eigenschaften der nach dem jeweiligen Modell möglichen Ele­mentarteilchen.
 
Edward Witten sieht deswegen als mögliche Kandidaten für das Modell unseres Universums vor allem jene Modelle der M-Theorie, in denen (den 3 real beobachteten Familien von Elementarteilchen entsprechend) die Calabi-Yau-Mannigfaltigkeiten 3 lochartige Trichter aufweisen: Jene nämlich führen zu einer Familien­bildung der vom Modell vorhergesagten Elementarteilchen, die der entspricht, die wir vom Standardmodell her kennen.
 
Nun: Selbst wenn man wirklich sehr gut passende Modelle findet, bedeutet das noch lange nicht, dass M-Theorie nicht Millarden weiterer kennt, die noch wesentlich besser passen.
 
 
Insbesondere kann M-Theorie nicht dadurch ad absurdum geführt werden,
 
dass in diesem oder jenem ihrer Modelle
 
Widersprüche zur Realität unseres Universums gefunden werden.
 
Hierdurch, so denke ich, wird es Physikern, die der Stringtheorie ablehnend gegenüberstehen,
 
fast unmöglich werden, sich durchzusetzen.
 
 
Umgekehrt scheint klar, dass der Weg hin zur Kenntnis der ersehnten Weltformel wohl auch mit Hilfe der M-Theorie von Menschen niemals wird zu Ende gegangen werden können. Neue Erkenntnisse schneller als bisher zu gewinnen, könnte sie aber wohl sicher helfen.
 
Hinweis nebenbei: Es gibt Varianten der Stringtheorie, in denen Strings auch negative Energie haben können, womit sie dann Tachyonen wären – Teilchen also, die sich schneller als das Licht bewegen könnten. Da Physiker nicht an Tachyonen glauben, sehen sie diese Varianten der Stringtheorie als nicht sinnvoll an. Tatsächlich aber hat man die in entsprechenden mathematischen Ausdrücken auftretenden Minuszeichen wohl nur noch nicht der richtigen Größe zugeordnet (so wie es im heute als überholt geltenden Modell der Dirac Sea ja auch mal war).

 

 

Henry aus 2049-8:

 
Die Stringtheorie(n) wurde entwickelt, um das Problem der Vereinigung aller vier Grundkräfte zu lösen,

Das ist nicht richtig, denn:

• Man hat die Stringtheorie zunächst nicht gezielt entwickelt, sondern überaschender Weise im wahrsten Sinne des Wortes  g e f u n d e n : Der Physiker Gabriele Veneziano entdeckt 1968 zufällig einen Zusammenhang zwischen der Eulerschen Betafunktion und der starken Kernkraft. Zwei Jahre später wird das Konzept der Strings in 26 Dimensionen eingeführt (bosonische Stringtheorie).

• Die Hoffnung, dass die Stringtheorie zur ersehnten Weltformel führen könnte, hatte man erst ab 1984 (sog. 1. String-Revolution), als niemand mehr der Theorie Anomalien vorwerfen konnte: Die wenigen Außenseiter, die sich davor mit Stringtheorie beschäftigt hatten, hatten Anomalien inzwischen beseitigen können.

Es ist nicht klar, wer die Stringtheorie als erster mit dem Stichwort "Weltformel" oder "Vereinheitlichung aller Kräfte" in Beziehung gesetzt sah (es muss 1984 oder kurz davor der Fall gewesen sein). Ab dann aber — und wirklich  e r s t  ab dann — hat sich ein Großteil aller theoretischen Physiker damit befasst.

Siehe auch: Stationen der Stringtheorie (1921 - 1996) in Wikibooks.

 

 

Irena aus 2049-18:

 
Meines Wissens gibt es die Stringtheorie nicht. Es gibt mehrere Theorien, die teilweise sich wiedersprechen. Muss ich noch mal mein Büchlein über Stringtheorie in die Hand nehmen und mein wissen auffrischen. Mindestens erinnere ich nicht, dass dabei die Rede über andere Universen war.

mfg

Grundsätzlich, Irena, hast Du recht:

Es gibt mehrere Varianten der Stringtheorie. Als letzter großer Fortschritt, den man gemacht hat, gilt jedoch:


1995 zeigt Edward Witten, dass die fünf bis dahin bekannten Stringtheorien nur Teilstücke einer übergeordneten Theorie sind,

die er M-Theorie nannte,

die aber im Grunde bis heute nur bekannt ist als etwas, das sich — je nachdem, wie man mathematisch rangeht — in Form eines dieser 5 Teile zeigt
( plus noch einer Variante, die Witten damals gleich mit entdeckt hat ) .

Wer also heute von "Stringtheorie" spricht, meint M-Theorie.

Eine bestimmte Stringtheorie ist letztlich nichts anderes als physikalische Deutung einer algebraischen Struktur S.

Nun weiß aber jeder Mathematiker: Sind S1 und S2 zwei algebraische Strukturen, so können die zueinander isomorph sein (womit sie dann — obgleich als Modell verschieden — als mathematischer Gegenstand ununterscheidbar sind: Worin sich zueinander isomorphe Strukturen unterscheiden ist lediglich Terminologie).

Dieselbe zentrale Rolle, die in der Mathematik Isomorphie spielt, kommt in der Physik dem Begriff der Dualität zu.

Zueinander duale Modelle sind nicht notwendig mathematisch isomorphe Modelle. Gerade in der Stringtheorie gibt es zueinander duale Modelle (solche also, die dieselbe Physik darstellen), die aber dennoch nicht mal in der Zahl der Dimensionen, die sie benötigen, übereinstimmen.

Auf Seite 485 seines Buches "The Fabric of the Cosmos" sagt Brian Greene:

Zitat:

 
More and more, these clues point toward the conclusion that the form of spacetime is an adorning detail that varies from one formulation of a physical theory to the next, rather than being a fundamental element of reality.

Much as the number of letters, syllables, and vowels in the word cat differ from those in gato, its Spanish translation, the form of spacetime — its shape, its size, and even the number of its dimensions — also changes in translation.
 

Gruß, grtgrt
 

Hi E...,

es freut mich, dass mir mal jemand sagt, wie mein Stil auf ihn wirkt. Danke also.

Damit Du mich besser verstehst, sei gesagt: Ich bin kein Physiker, die Art meiner Argumentation ist aber sicher dadurch geprägt, dass ich mal Mathematiker war (mit Schwerpunkt auf Algebra und Zahlentheorie), dann aber — seit etwa 1980 — stets als Informatiker gearbeitet habe (als IT-Berater mit Schwerpunkt auf besonders methodischem Software-Engineering).

Mein Interesse an theoretischer Physik wurde geweckt durch die Beobachtung, dass theoretische Physiker sich von Science Fiction Autoren des Typs Isaac Asimov eigentlich nur dadurch unterscheiden, dass sie versuchen, ihre visionären Gedanken über die Natur und die Struktur unserer Welt nicht nur aufzuschreiben, sondern auch zu beweisen oder zu widerlegen.

Bester Weg hierfür, da gebe ich Dir recht, wäre die Durchführung geeigneter Experimente. Dieser Weg aber stößt schnell an Grenzen (an prinzipielle, weit vorher aber noch an finanzielle). Wo sie erreicht sind, ist Informationsverarbeitung der einzige Weg, weiter zu kommen. Sie muss erfolgen in geschickter Kombination mathematischer und ingenieurmäßiger Denkwege.

Wenn man nicht zufällig ein Albert Einstein ist, kann man sich Erfolge dennoch nur erhoffen, wenn man so viel wie möglich auf den Gedanken anderer aufbaut. Wie jeder Promovierte weiß, ist eigene Leistung i.A. ja nur ein nächster kleiner Schritt hin zum Ziel. Man geht ihn in der Hoffnung, dass andere ihn aufgreifen und so ihrerseits in die Lage versetzt werden, die Entfernung zum Ziel weiter zu verkleinern.

Versetzen wir uns jetzt in die Rolle dieser anderen. Die Wahrscheinlichkeit, dass sie einen noch unvollständigen Weg aufgreifen, wird umso größer sein, je wertvoller er ihnen erscheint (sprich: aus je mehr Schritten er schon besteht). Wenn ich also einen (N+1)-sten Schritt in die Welt setze, tue ich gut daran, nicht zu verbergen, dass er nicht der erste Schritt des langen Weges hin zur Erkenntnis ist, sondern nur ein weiterer, vielleicht aber wirklich notwendiger.

Das also ist der Grund, warum ich nur ungern isolierte Ideen in die Welt setzte. Mir ist viel wohler, wenn ich die Ideen anderer extrapoliere. Nicht zuletzt gibt das mir und denen, die mir folgen, ja auch eine gewisse Sicherheit, nicht völlig schief zu liegen — solche Sicherheit zu suchen sehe ich nicht als Schwäche sondern als Teil jeder professionellen Vorgehensweise.


Nun zu den Strings: Sie modellieren ganz klar Elementarteilchen (virtuelle und auch stabile, wie etwa die Elektronen und Positronen). Und die existieren ja nun wirklich. Und dass Elementarteilchen in Schwingung befindliche Energiequanten sind, gilt ja nun auch schon längst als gesichertes Wissen.

Das Fragezeichen, das man neben die Stringtheorie zu setzen hat, steht also weniger am Begriff der Strings (oder Branen), sondern steht vor allem an den Vorhersagen, die die Stringtheorie in Hinsicht auf Sysmmetrie und Vollständigkeit des Standardmodells der Elementarteilchenphysik macht. Es steht insbesondere an allen Aussagen, die unserem Universum weitere Dimensionen zugestehen wollen oder gar noch bestimmte Krümmung jener.

Jene Fragezeichen sind den Stringtheoretikern selbst sehr wohl bewusst: Greene etwa schreibt (auf Seite 485 seines Buches The Fabric of the Cosmos): "More and more, ... clues point toward the conclusion that the form of spacetime is an adorning detail that varies from one formulation of a physical theory to the next, rather than being a fundamental element of reality. Much as the number of letters, syllables, and vowels in the word cat differ from those in gato, its Spanish translation, the form of spacetime — its shape, its size, and even the number of its dimensions — also changes in translation."

Mir ist sehr wohl klar, dass es durchaus Fachleute gibt, die der Stringtheorie sehr skeptisch gegenüber stehen:

• Mir ist bekannt, dass Peter Woit (mir scheint, er wird wohl nur seines provokativen Buches wegen so oft genannt) so weit geht, zu sagen, dass Fördergelder, die an Stringtheoretiker gegeben werden, Geldverschwendung seien. Nachvollziehbare Argumente hat er in meinen Augen aber nicht, und seine Behauptung, die Stringtheorie sei bisher nicht in der Lage gewesen irgendwelche Vorhersagen zu machen, wirkt nicht so recht glaubhaft, wenn man weiß, dass er sich mehr mit Mathematik als mit Physik beschäftigt (also vielleicht nicht wirklich Fachmann ist) und dass viele Physiker ihm widersprechen: In WikiBooks findet sich eine Liste von 12 Vorhersagen der Stringtheorie, die man durchaus als schon verifiziert ansieht).

• Andere, wie etwa Roger Penrose, sind skeptisch, versuchen aber dennoch — wie es sich für Wissenschaftler gehört — objektiv zu bleiben und machen sich wenigstens die Mühe, den Stringtheoretikern ernsthaft zuzuhören.

• Einer von ihnen ist sicher auch Lee Smolin. Der aber sieht vor allem deswegen wenig Sinn darin, Stringtheorie zu betreiben, da sie sich in Bereiche vorwagt, in denen die Experimentalphysik wohl niemals wird Aussagen machen können (siehe dieses Interview mit ihm). So zu argumentieren ist nachvollziehbar, zeugt aber vielleicht doch eher von fehlendem Mut, über bestehende Grenzen hinauszudenken.

Ich sage: Solange die Stringtheorie keine Aussage macht, die im Widerspruch zu mindestens einem anerkannten Ergebnis der Experimentalphysik steht, kann auf keinen Fall behauptet werden, sie sei ein Irrweg.

Peter Woit scheint diese Logik zu ignorieren (was mir seine Meinung recht suspekt macht). Smolins Buch dagegen sollte man gelesen haben (aber: Wichtige Erfolge der Stringtheorie, über die Greene 2010 berichtet, scheint Smolin 2006 nicht zu kennen. Ob das Uneinigkeit in der Beurteilung bedeutet oder darauf zurückzuführen ist, dass jene Ergebnisse damals vielleicht noch gar nicht erarbeitet waren, weiß ich nicht).

Beste Grüße,
grtgrt = ggreiter = Gebhard Greiter

Mein Motto: Die beste Praxis ist eine gute Theorie (nach E... Denert, einer der beiden Gründer von sd&m)