Wie Zeitdilatation und Dopplereffekt die Zeit relativ machen
Wir betrachten zwei Objekte — A und B —, die sich relativ zu einander bewegen.Für beliebige Objekte X und Y stehe Z(X:Y) für durch Y von der Uhr von X abgelesene Zeit im Sinne von Y.
Es sei dann v der Vektor der Geschwindigkeit, die A in einem Koordinatensystem hat, in dessen Ursprung B sitzt, und es sei weiter v die Länge des Vektors v.
Mit dem Zeitdilatationsfaktor γ(v) = ( 1 – (v/c)2 )-1/2 [dem sog. LORENTZ-Faktor] ergibt sich die dem B im Vergleich zu seiner eigenen Uhr als gedehnt erscheinende Zeit Z(A:B) des beobachteten Objekts A — im Falle, dass A sich unbeschleunigt in Beobachtungsrichtung vom B wegbewegt — durch die einfache Formel
Im Falle unbeschleunigter Bewegung generell muss man folgende, etwas kompliziertere Formel anwenden:
worin Z(B) = Z(B:B) die durch B von der eigenen Uhr abgelesene Zeit bezeichnet, φ den Winkel zwischen dem Geschwindigkeitsvektor v und dem Vektor von B nach A, und vabst = v cos(φ) die erste Ableitung des Abstandes zwischen A und B aus Sicht von B nach der Zeit Z(B) (s. Wikipedia: Doppler-Effekt bei diesem oder jenem Winkel).
Dies gilt näherungsweise, da die Differenz ( 1 – vabst/c ) erster Term einer Tailor-Entwicklung ist, die dort eigentlich (statt seiner) stehen müsste.
Und natürlich ist in all dem c die Lichtgeschwindigkeit im Vakuum.
Man erkennt:
- Nur wenn A sich in einem Kreis um B herum bewegt, wird vabst = 0 , dann also Zu(A:B) = Z(A:B).
- Die Gleichung vabst = v gilt nur, solange A sich aus Sicht von B in stets gleicher Richtung findet.
- In voller Allgemeinheit — auch, wenn nicht konstante Beschleunigung mit zu berücksichtigen ist — wird der Zeitdilatationseffekt durch die Lorentz-Transformation beschrieben.
( x’, ct' ) = ( ( x – v/c * ct ), ( ct – v/c * x ) ) γ(v)
Besonders gut verstehbar wird die Lorentz-Transformation anhand sog. Minkowski-Diagramme, wie sie z.B. John Denker umfassend erklärt.
Mit Hilfe des Dopplereffekts lässt sich auch das sog. Zwillingsparadoxon verstehen, das in den 1920-er Jahren die Öffentlichkeit stark beschäftigt hat:
-
Ein Zwilling eines Paares macht eine Reise mit einem Raumfahrzeug, das zunächst sehr schnell gerade aus fliegt, dann aber die Richtung wechselt und zurückkehrt.
War die Geschwindigkeit des reisenden Zwillings das Produkt aus Lichtgeschwindigkeit und der halben Wurzel aus 3 und zeigte die mitgeführte Uhr eine Reisedauer von 10 Jahren an, so hat der zurückgebliebene Bruder 20 Jahre verstreichen sehen.
Die Analyse von kontinuierlich während der Reisezeit hin- und hergesandten Signalen ergibt unter Berücksichtigung von Dopplereffekt und Längenkontraktion, dass beide Zwillinge darin übereinstimmen, dass der Reisende jünger geblieben ist. [Natürlich nur, wenn angenommen wird, dass die seine Lebenszeit messende biologische Uhr sich wie eine physikalische Uhr verhält].
Quelle: Hubert Goenner: Einsteins Relativitätstheorien (2016, 6. Auflage), S. 40-43 [Goenner lehrte als Professor für Theoretische Physik an der Uni Göttingen].
Nochmals sei wiederholt: Die in Sachbüchern oft genannten einfachen Formeln
ΔxA:B = γ(v)-1 ΔxB:B
ΔtA:B = γ(v) ΔtB:B
gelten nur für Bewegung, die in Blickrichtung weg vom Beobachter führt.
Wenn relativ zu einander bewegte Beobachter räumliche oder zeitliche Abstände quantifizieren, werden sie i.A. zu unterschiedlichem Ergebnis kommen.
Nebenbei noch: Ein Spezialfall des Anteils der Zeitdilation, der des Dopplereffekts wegen entsteht, ist die sog. kosmologische Zeitdilatation.
Sie ist Folge der Expansion des Raumes, d.h. Folge der Tatsache, dass die Abstände weit von einander entferner Galaxien sich ständig vergrößern.
Gut zu beobachten ist sie anhand der Lichtkurven sämtlicher Supernovae vom Typ Ia:
Eigentlich läuft die Physik dieser Sternexplosionen immer wieder gleich ab und folglich sollten die Lichtkurven mit der gleichen Zeitskala abklingen. Die Astronomen beobachten jedoch, dass die beobachtete Lichtkurve umso breiter ist, je weiter die Supernova entfernt ist (siehe Abbildung). Das ist gerade der kosmologische Zeitdilatationseffekt: Je weiter entfernt von uns Sternexplosionen auftreten, desto langsamer klingen sie aus Sicht irdischer Astronomen ab. Als Astronom muss man diesen Effekt natürlich herausrechnen, um kosmologische Parameter zu bestimmen (was heutzutage aber schon Routine bei der Auswertung ist).
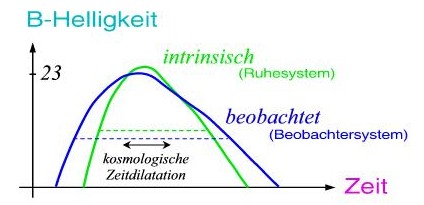
Quelle: Spektrum der Wissenschaft, Nov. 2019
stw6048ZDP — Zeitdilatation . Dopplereffekt . Physik — News?
Mehr + B G E + S H A + More
Von Lichtuhren zur Zeitdilatation
Lesenswertes Skript zur SRT
The most general Lorentz Transformation
Twins and Clocks in Einsteins Theory: Relativität richtig verstanden