welt-verstehen/Kiefer+Zwillingsparadoxon+Relativitätstheorie+Dopplereffekt+Altersunterschied, stw9320KZRDA
Unsere Welt zu verstehen: Kiefer Zwillingsparadoxon
Beitrag 0-342
Claus Kiefer erklärt das Zwillingsparadoxon richtig
— Joachim Schulz aber, der ihm widerspricht, denkt nicht weit genug —
Quelle: Claus Kiefer: Der Quantenkosmos, Fischer 2008, S. 36-37
Claus Kiefer studierte Physik und Astronomie. Er promovierte 1988 über den Begriff der inneren Zeit in der kanonischen Quantentheorie der Gravitation. Nach seiner Habilitation lehrte er an den Universitäten in Zürich und Freiburg. Seit 2001 ist der Professor für Theoretische Physik an der Universität Köln.
Joachim Schulz ist promovierter Physiker, aber kein Experte für Relativitätstheorie.
Bei seiner Argumentation in [JS] übersieht Schulz, dass nur unterschiedliche Beschleunigung der Zwillinge ihre Weltlinien unterschiedlich lang machen kann. Dies ergibt sich allein schon aus Symmetriegründen.
Dennoch kommt — wie Schulz ganz richtig zeigt — der Altersunterschied auch in Phasen zustande, in denen keine Beschleunigung vorliegt. Er kommt also zustande
Reisegeschwindigkeit sowie Lage und Krümmung der Weltlinie des reisenden Zwillings werden durch seine Beschleunigung bestimmt.
Damit gilt gleiches für seinen Verbrauch an Eigenzeit während der Reise, denn der entspricht der Länge der Weltlinie.
Hier nun, wie sich das einsehen lässt:
Ganz analog zur Argumentation von Joachim Schulz ist jene von Martin Bäker im Abschnitt » The Good « seines Blog Posts Erklärungen zum Zwillingsparadoxon, wo Bäker argumentiert wie folgt:
Statt, wie Bäker, auf den Bonus hinzuweisen, argumentiere ich wie folgt:
Konsequenz daraus: Das uns durch das Bild 1 nahegelegte Rechenmodell ist — während der gesamten Umkehrphase — allzu unrealistisch — so dass man seinem Ergebnis nicht trauen kann.
Gleiches gilt für das dazu analoge Rechenmodell von Joachim Schulz, welches ja ebenfalls sämtliche beschleunigten Phasen der Reise als unteilbare Augenblicke annimmt.
In vollem Umfang richtig — auch hinsichtlich der mindestens am Umkehrpunkt notwendigen Beschleunigungsphase — wird die Situation nun aber dargestellt im Diagramm hier (man beachte die dünnen roten Linien, welche in Bäkers Diagramm den dort blau und rot gezeigten entsprechen):

Erst dieses Bild und das nächste machen klar, dass
sich das Zwillingsparadoxon allein schon mit Hilfe der SRT in überzeugender Weise lösen lässt
und in welcher Weise der Dopplereffekt sich bemerkbar macht:
Für den entstehenden Altersunterschied der Zwillinge spielt er keine Rolle,
wohl aber für die Ankunftszeiten zwischen A und B ausgetauschter Nachrichten.
Wie man sieht, ist der Weg, den B durch den Raum nimmt, gekrümmt.
Diese Krümmung verlängert in der Formel für die Minkowski-Metrik den raumartigen Anteil der raumzeitlichen Distanz und
verkürzt
deswegen entsprechend ihren zeitartigen Anteil,
d.h. die Eigenzeit von B im Vergleich zur Eigenzeit von A zwischen Antritt und Ende der Reise.
Wie man ferner sieht, bleibt in nichtbeschleunigten Phasen der Reise der Prozentsatz, zu dem die Eigenzeit von B der Eigenzeit von A gegenüber gedehnt ist, konstant.
Andere Dehnung der Eigenzeit von B ergibt sich (vorzeichenrichtig) erst wieder, wenn B beschleunigt (bzw. abbremst).
In diesem Diagramm wird das nur deswegen nicht deutlich, da es beschleunigte Phasen ja gar nicht zeigt (bzw. auflöst).
Solche einfachen Diagramme zeigen also nicht jede Sicht der Zwillinge, sondern einfach nur ihre jeweilge Sicht aus den 3 Perspektiven heraus, welche den Phasen unbeschleunigter Bewegung entsprechen.
Im folgenden Bild sind diese drei Sichten auf ein und dieselbe Raumzeit farblich unterschieden dargestellt:
Die punktierte Linie darin ist die durch die Raumzeit führende Weltlinie des Lichts.
Die geraden unterbrochenen Linien (jeweils parallel zur Raumachse einer Sicht) stellen dar, was aus jeder einzelnen dieser 3 Sichten heraus gleichzeitig geschieht.
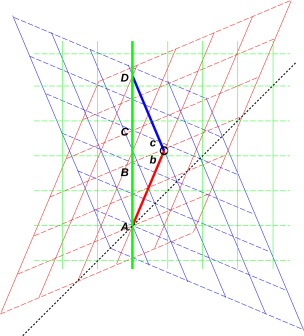
Quelle: John Denker (2003)
Bild 4 zeigt sehr deutlich, dass Beschleunigung nicht die Struktur der Raumzeit verändert, sondern lediglich die Sicht des Beschleunigten auf die Raumzeit: Das Koordinatensystem, aus dem heraus er die Welt betrachtet, dreht sich während seiner Beschleunigung mehr und mehr, so dass seine Raumachse neue Richtung bekommt). Bild 2 zeigt, dass dies bei wachsender Beschleunigung eine Drehung gegen den Uhrzeigersinn, bei fallender Beschleunigung aber eine im Uhrzeigersinn ist (wenn Serenas Reiseziel sich rechts im Bild findet).
Bild 2 zeigt auch, dass Beschleunigung den Weg durch die Raumzeit krümmt und somit kürzer macht.
Nur dieser Krümmung wegen, die es ohne Beschleunigung nicht gegeben hätte, ergibt sich für die Zwillinge ein nicht mehr rückgängig zu machender Altersunterschied.
Joachim Schulz irrt demnach gründlich, wenn er behauptet nicht Beschleunigung mache die Zeit (sprich: den Altersunterschied).
Richtig ist stattdessen:
Beschleunigung bestimmt Eigenzeit, Geschwindigkeit bestimmt das Messergebnis (sprich: die Zeit als beobachteten Fluss der Zeit).
Was wir Zeit nennen, ist gemessene Zeit,
d.h. durch stetige Abstandsänderung und die Endlichkeit der Lichtgeschwindigkeit relativ gewordenes Ergebnis
einer Beobachtung des Flusses der Eigenzeit des beobachteten Objekts.
Fußnote:
Nachdem ich versucht habe, zentrale Aussagen diese Seite im Rahmen der Kommentare #470-#718 zu Martin Bäkers Blogpost qualitätsgesichert zu bekommen, wurde mir gegen Ende der Diskussion dort klar, dass — Missverständnisse zu vermeiden — klar sein sollte, wie ich und meine Diskussionspartner dort die 4 Diagramme oben lesen. Wir lesen sie wie folgt:
Grenzwertbetrachtung
Zur Kenntnis nehmen sollte man, dass Bild 2 in Kombination mit der Erkenntnis, dass der schließlich für die Zwillinge entstehende Altersunterschied prozentual umso deutlicher ausfallen wird, je höher die Beschleunigung ist, mit der B die Reise durchführt, auch noch zeigt:
Extrem hohe Beschleunigung gleich von Anfang an — ebenso wie zu Beginn der Rückreise — führt schnell zu hoher Geschwindigkeit und damit zu schnellerem Erreichen des Ziels, so dass A weniger lange auf die Rückkehr von B zu warten hat.
Die Bilder 1 und 2 werden dadurch niedriger (bei gleicher Breite) und der Winkel zwischen den Raumachsen der beiden Zwillinge könnte so gut auf bis fast 90 Grad wachsen (immer vorausgesetzt, B hält so hohe Beschleunigung aus, was aber gut sein könnte, wenn B keine Person, sondern nur eine Uhr ist). Je entschiedener also beschleunigt wird, desto mehr führt die Weltlinie von B dann fast nur noch durch den Raum, also fast gar nicht mehr durch die Zeit.
Ihre am Umkehrpunkt dann zunehmend stärker werdende Krümmung korresponiert mit dem gegen Null strebenden Verhältnis Eigenzeit(B)/Eigenzeit(A).
Grenzübergang zeigt:
Was sich mit Lichtgeschwindigkeit durch den Raum bewegt
— Licht etwa oder Gravitationswellen —
altert gar nicht.
aus Notizen zu
Das Zwillingsparadoxon im Lichte von SRT und ART
Impressum
— Joachim Schulz aber, der ihm widerspricht, denkt nicht weit genug —
Claus Kiefer (wörtlich zitiert):
[ Im Szenario des Zwillingsparadoxons ] verlässt ein Zwilling die Erde mit einem Raumschiff, während sein Bruder auf der Erde verbleibt. Der Raumfahrer rast mit hoher Geschwindigkeit ins All, kehrt um und rast wieder zur Erde zurück. Bei seiner Rückkehr stellt er fest, dass sein Bruder im Vergleich zu ihm gealtert ist. Wie lässt sich das verstehen?
Da wegen der Zeitdilatation alle Uhren (und somit auch alle physiologischen Vorgänge im Raumschiff) in bezug auf den irdischen Zwilling verlangsamt sind, ist ja zu erwarten, dass der Raumfahrer zum Zeitpunkt seiner Rückkehr weniger gealtert ist.
Doch gilt dies nicht auch umgekehrt? Ist nicht der irdische Zwilling in bezug auf seinen Bruder im Raumschiff bewegt und sollte deshalb weniger altern?
Der Pferdefuß bei dieser Gedankenkette liegt darin, dass der Raumfahrer Beschleunigung erfährt, der irdische hingegen nicht (jedenfalls in guter Näherung). Um nämlich umkehren zu können, muss der reisende Zwilling seine Geschwindigkeit ändern. Das Relativitätsprinzip gilt jedoch nur für Initialsysteme, nicht für beschleunigte Systeme. Von daher ist die Symmetrie zwischen beiden Zwillingen gebrochen.
In Minkowskis Raumzeitformulierung lässt sich leicht erkennen, dass der irdische Zwilling bei Rückkehr älter ist:
Die verflossene Zeit, die der jeweilige Zwilling auf seiner Uhr abliest — man spricht hier von sog. Eigenzeit —, lässt sich direkt aus der Länge der jeweiligen Weltlinien im Minkowski-Raum ablesen.
Umgekehrt zur rein räumlichen Geometrie gilt aber, dass die längste Zeit für einen Beobachter auf einer geraden Weltlinie vergeht. Jede Krümmung verkürzt die Eigenzeit. Da die Weltlinie des reisenden Zwillings gekrümmt ist, entspricht ihr im Vergleich zur Weltline des irdischen Zwillings eine kleinere Eigenzeit.
Claus Kiefer studierte Physik und Astronomie. Er promovierte 1988 über den Begriff der inneren Zeit in der kanonischen Quantentheorie der Gravitation. Nach seiner Habilitation lehrte er an den Universitäten in Zürich und Freiburg. Seit 2001 ist der Professor für Theoretische Physik an der Universität Köln.
Joachim Schulz ist promovierter Physiker, aber kein Experte für Relativitätstheorie.
Bei seiner Argumentation in [JS] übersieht Schulz, dass nur unterschiedliche Beschleunigung der Zwillinge ihre Weltlinien unterschiedlich lang machen kann. Dies ergibt sich allein schon aus Symmetriegründen.
Dennoch kommt — wie Schulz ganz richtig zeigt — der Altersunterschied auch in Phasen zustande, in denen keine Beschleunigung vorliegt. Er kommt also zustande
- ganz wesentlich unterschiedlicher Beschleunigung wegen,
- aber dennoch nicht nur während der beschleunigten Phasen der Reise.
Damit gilt gleiches für seinen Verbrauch an Eigenzeit während der Reise, denn der entspricht der Länge der Weltlinie.
Hier nun, wie sich das einsehen lässt:
Ganz analog zur Argumentation von Joachim Schulz ist jene von Martin Bäker im Abschnitt » The Good « seines Blog Posts Erklärungen zum Zwillingsparadoxon, wo Bäker argumentiert wie folgt:
Martin Bäker (analog zu Schulz):
Entscheidend ist anscheinend nicht die Beschleunigung, sondern etwas anderes. Das wird beispielsweise in dieser Grafik deutlich:
Betrachtet werden ein stationärer Zwilling (Teresa = A) und ein reisender (Serena = B):
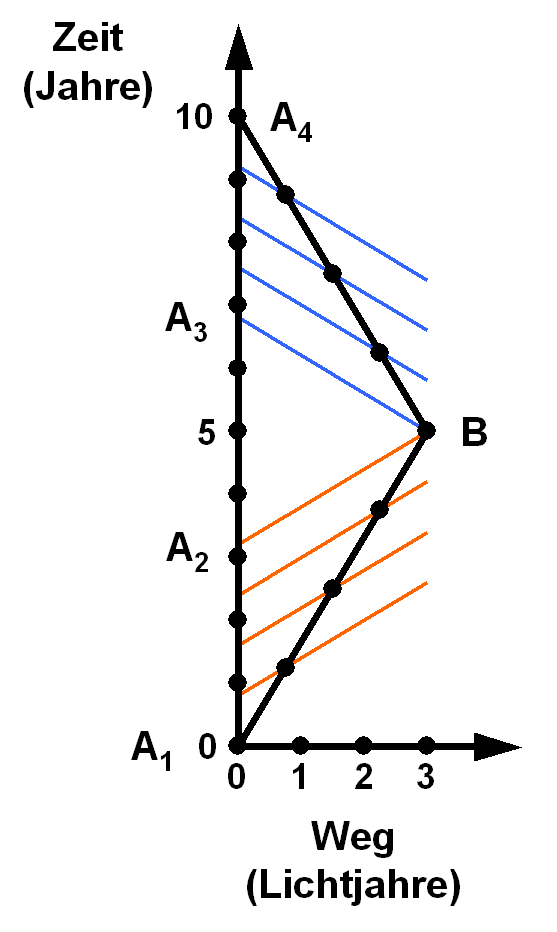
Das Bild zeigt den Weg von Serena (B) bis in 3 Lichtjahre Entfernung mit einer Geschwindigkeit von 60% der Lichtgeschwindigkeit und anschließender Rückkehr eingetragen in einem Raumzeit-Diagramm. Auf der horizontalen Achse ist der Ort (gemessen von A aus) aufgetragen, auf der vertikalen Achse die Zeit, die für A vergeht. Die Punkte liegen (auf der jeweiligen Achse) im Abstand von einem Jahr. Die roten und blauen Linien zeigen, welche Ereignisse für B jeweils zur selben Zeit stattfinden.
Wenn B (Serena) von A wegfliegt, dann sieht sie A (Teresa) verlangsamt, die rote Linie, die bei Serenas zweitem Punkt (also nach zwei Jahren) liegt, trifft die senkrechte Achse, die Teresa beschreibt, an einem Punkt, wo für Teresa weniger als zwei Jahre vergangen sind.
Umgekehrt zeigt eine horizontale Linie, die ihr euch bei Teresa zur Zeit nach zwei Jahren denkt, dass hier für Serena weniger als 2 Jahre vergangen sind, die Situation ist also symmetrisch. Auf dem Rückflug ist es ähnlich, auch hier könnt ihr euch leicht überzeugen, dass jede die anderen verzögert sieht (am einfachsten fangt ihr dazu oben an und guckt sozusagen in die Vergangenheit, dann ist das Bild ja genau symmetrisch).
Entscheidend aber ist — und das macht dieses Diagramm sehr schön deutlich —, dass es einen weiten Bereich von Ereignissen bei Teresa (A) gibt, die für den reisenden Zwilling (Serena = B) mit gar nichts gleichzeitig sind. Und das hat nichts mit irgendwelchen Beschleunigungen zu tun, sondern nur damit, dass Serena ihr Bezugssystem wechselt.
Das Zwillingsparadoxon kommt demnach durch einen Wechsel des Bezugssystems zustande (rein rechnerisch wenigstens).
So ein Wechsel des Bezugssystems kann in der Physik oft zu scheinbaren Unstimmigkeiten in der Beschreibung führen, ein Beispiel dafür habe ich vor einiger Zeit hier erklärt mit Auflösung des Rätsels hier.
Wikipedia zeigt übrigens auch noch eine Grafik, die den Fall einer kontinuierlichen Beschleunigung veranschaulicht — auch da sieht man nochmal, dass die SRT wirklich und tatsächlich kein Problem hat, mit Beschleunigungen zu hantieren.
Physikalisch ist das sicherlich eine sehr saubere und sinnvolle Erklärung, die kein bisschen in die Irre führt. Allerdings ist dieser Wechsel des Bezugssystems (seine Folgen betreffend) nicht wirklich anschaulich. Man denkt, er könne nur beschreibungstechnische Bedeutung haben. Deswegen nun — sozusagen als Bonus — das Märchen bzw. Paradoxon von Raum und Zeit: ... [man sollte seine Lösung genau durchdenken].
Statt, wie Bäker, auf den Bonus hinzuweisen, argumentiere ich wie folgt:
Nach Bild 1 besteht die Umkehrphase aus nur einem einzigen Ereignis, was so in Wirklichkeit aber nie sein kann. Genauer:
Bild 1 suggeriert uns, es gäbe für Serena nur zwei Bezugssysteme: das der Hinreise und das der Rückreise. Tatsächlich aber wird Serenas Bezugssystem stetig gedreht – als Initialsystem also ständig ausgetauscht – während aller Phasen ihrer Reise, in denen sie sich beschleunigt bewegt.
Die Steigung der dicken roten Linie zeigt die Geschwindigkeit von Serena (relativ zu Teresa).
Konsequenz daraus: Das uns durch das Bild 1 nahegelegte Rechenmodell ist — während der gesamten Umkehrphase — allzu unrealistisch — so dass man seinem Ergebnis nicht trauen kann.
Gleiches gilt für das dazu analoge Rechenmodell von Joachim Schulz, welches ja ebenfalls sämtliche beschleunigten Phasen der Reise als unteilbare Augenblicke annimmt.
In vollem Umfang richtig — auch hinsichtlich der mindestens am Umkehrpunkt notwendigen Beschleunigungsphase — wird die Situation nun aber dargestellt im Diagramm hier (man beachte die dünnen roten Linien, welche in Bäkers Diagramm den dort blau und rot gezeigten entsprechen):

sich das Zwillingsparadoxon allein schon mit Hilfe der SRT in überzeugender Weise lösen lässt
und in welcher Weise der Dopplereffekt sich bemerkbar macht:
Für den entstehenden Altersunterschied der Zwillinge spielt er keine Rolle,
wohl aber für die Ankunftszeiten zwischen A und B ausgetauschter Nachrichten.
Wie man sieht, ist der Weg, den B durch den Raum nimmt, gekrümmt.
Diese Krümmung verlängert in der Formel für die Minkowski-Metrik den raumartigen Anteil der raumzeitlichen Distanz und
verkürzt
deswegen entsprechend ihren zeitartigen Anteil,
d.h. die Eigenzeit von B im Vergleich zur Eigenzeit von A zwischen Antritt und Ende der Reise.
Wie man ferner sieht, bleibt in nichtbeschleunigten Phasen der Reise der Prozentsatz, zu dem die Eigenzeit von B der Eigenzeit von A gegenüber gedehnt ist, konstant.
Andere Dehnung der Eigenzeit von B ergibt sich (vorzeichenrichtig) erst wieder, wenn B beschleunigt (bzw. abbremst).

In diesem Diagramm wird das nur deswegen nicht deutlich, da es beschleunigte Phasen ja gar nicht zeigt (bzw. auflöst).
Solche einfachen Diagramme zeigen also nicht jede Sicht der Zwillinge, sondern einfach nur ihre jeweilge Sicht aus den 3 Perspektiven heraus, welche den Phasen unbeschleunigter Bewegung entsprechen.
Im folgenden Bild sind diese drei Sichten auf ein und dieselbe Raumzeit farblich unterschieden dargestellt:
Die punktierte Linie darin ist die durch die Raumzeit führende Weltlinie des Lichts.
Die geraden unterbrochenen Linien (jeweils parallel zur Raumachse einer Sicht) stellen dar, was aus jeder einzelnen dieser 3 Sichten heraus gleichzeitig geschieht.

Quelle: John Denker (2003)
Bild 4 zeigt sehr deutlich, dass Beschleunigung nicht die Struktur der Raumzeit verändert, sondern lediglich die Sicht des Beschleunigten auf die Raumzeit: Das Koordinatensystem, aus dem heraus er die Welt betrachtet, dreht sich während seiner Beschleunigung mehr und mehr, so dass seine Raumachse neue Richtung bekommt). Bild 2 zeigt, dass dies bei wachsender Beschleunigung eine Drehung gegen den Uhrzeigersinn, bei fallender Beschleunigung aber eine im Uhrzeigersinn ist (wenn Serenas Reiseziel sich rechts im Bild findet).
Bild 2 zeigt auch, dass Beschleunigung den Weg durch die Raumzeit krümmt und somit kürzer macht.
Nur dieser Krümmung wegen, die es ohne Beschleunigung nicht gegeben hätte, ergibt sich für die Zwillinge ein nicht mehr rückgängig zu machender Altersunterschied.
Joachim Schulz irrt demnach gründlich, wenn er behauptet nicht Beschleunigung mache die Zeit (sprich: den Altersunterschied).
Richtig ist stattdessen:
Beschleunigung bestimmt Eigenzeit, Geschwindigkeit bestimmt das Messergebnis (sprich: die Zeit als beobachteten Fluss der Zeit).
Was wir Zeit nennen, ist gemessene Zeit,
d.h. durch stetige Abstandsänderung und die Endlichkeit der Lichtgeschwindigkeit relativ gewordenes Ergebnis
einer Beobachtung des Flusses der Eigenzeit des beobachteten Objekts.
Fußnote:
Nachdem ich versucht habe, zentrale Aussagen diese Seite im Rahmen der Kommentare #470-#718 zu Martin Bäkers Blogpost qualitätsgesichert zu bekommen, wurde mir gegen Ende der Diskussion dort klar, dass — Missverständnisse zu vermeiden — klar sein sollte, wie ich und meine Diskussionspartner dort die 4 Diagramme oben lesen. Wir lesen sie wie folgt:
- Zum 1. Bild: Es besteht Einigkeit darüber, dass es die für Serena notwendigen Beschleunigungsphasen ignoriert — genauer: als Phasen zeitlicher Länge Null betrachtet,
was man als realitätsfern einzustufen hat — und dass ferner gilt:
Die roten und blauen Linien zeigen, welche Ereignisse aus Sicht des reisenden Zwillings (B = Serena) jeweils zur selben Zeit stattfinden.
- Zum 2. Bild: Die waagrechten dünnen blauen Linien zeigen, welche Ereignisse in Teresa Koordinatensystem gleichzeitig sind.
Die dünnen roten Linien zeigen, welche Ereignisse im jeweiligen Koordinatensysten von Serena (dem reisenden Zwilling B) zur Zeit seiner Hinreise, Umkehr und Rückreise gleichzeitig sind.
Die dickeren roten Punkte markieren die Zeitpunkte, zu denen der rote Zwilling die Eigenbeschleunigung ändert.
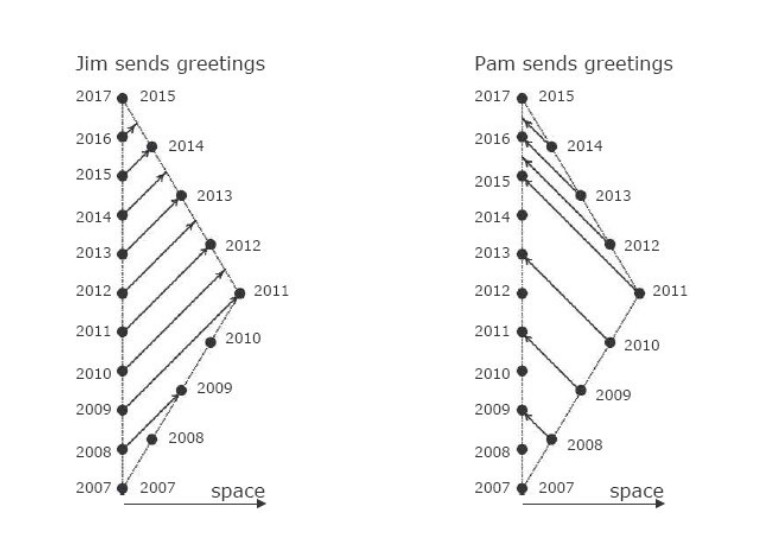
- Zum 3. Bild: Es zeigt, zu welcher Zeit durch A oder B abgesandte Signale (über Funk abgesetzte Greetings) bei der Schwester ankommen.
Deutlich erkennbar im Bild ist der Dopplereffekt.
- Zum 4. Bild: Es zeigt, wie ein und dieselbe Raumzeit sich unter den Koordinatensystemen darstellt, welche genutzt werden
- von Teresa die ganze Zeit über (das grüne),
- von Serena während der unbeschleunigten Phase ihrer Hinreise zum Umkehrpunkt (das rote), bzw.
- von Serena während der unbeschleunigten Phase ihrer Rückreise (das blaue).
Extrem deutlich wird die Relativität der Gleichzeitigkeit: Gleichzeitig zu sein bedeutet, im jeweils genutzten Koordinatensystem denselben ct-Wert zu haben.
Deutlich wird auch, dass die Weltlinie des Lichts — so wie man das von allen Weltlinien erwartet — ein NICHT relativer Begriff ist.
Wo unterschiedliche Ereignisse auf ihr liegen, haben sie raumzeitlichen Abstand ds = 0 (man sagt dann auch, sie hätten lichtartigen Abstand).
Wenn wir einen fernen Stern beobachten, ist das ein Ereignis, welches lichtartigen Abstand hat von dem Ereignis, in dem der Stern — irgendwann in seiner Vergangenheit — das Bild seiner selbst abgestrahlt hat, das wir eben jetzt empfangen. - von Teresa die ganze Zeit über (das grüne),
Zur Kenntnis nehmen sollte man, dass Bild 2 in Kombination mit der Erkenntnis, dass der schließlich für die Zwillinge entstehende Altersunterschied prozentual umso deutlicher ausfallen wird, je höher die Beschleunigung ist, mit der B die Reise durchführt, auch noch zeigt:
Extrem hohe Beschleunigung gleich von Anfang an — ebenso wie zu Beginn der Rückreise — führt schnell zu hoher Geschwindigkeit und damit zu schnellerem Erreichen des Ziels, so dass A weniger lange auf die Rückkehr von B zu warten hat.
Die Bilder 1 und 2 werden dadurch niedriger (bei gleicher Breite) und der Winkel zwischen den Raumachsen der beiden Zwillinge könnte so gut auf bis fast 90 Grad wachsen (immer vorausgesetzt, B hält so hohe Beschleunigung aus, was aber gut sein könnte, wenn B keine Person, sondern nur eine Uhr ist). Je entschiedener also beschleunigt wird, desto mehr führt die Weltlinie von B dann fast nur noch durch den Raum, also fast gar nicht mehr durch die Zeit.
Ihre am Umkehrpunkt dann zunehmend stärker werdende Krümmung korresponiert mit dem gegen Null strebenden Verhältnis Eigenzeit(B)/Eigenzeit(A).
Grenzübergang zeigt:
— Licht etwa oder Gravitationswellen —
altert gar nicht.
tags: stw2475K: Kiefer+Zwillingsparadoxon+Relativitätstheorie+Dopplereffekt+Altersunterschied
Das Zwillingsparadoxon im Lichte von SRT und ART
Impressum