Zum Realitätsbegriff in der Physik
Beitrag 0-35
Realität ist eher nur selten Wirklichkeit
Schon Platons Höhlengleichnis hat versucht, zu erklären:
Realität ist etwas durch unseren Verstand Konstruiertes (etwas Subjektives).
Erst Wirklichkeit ist das objektiv Vorhandene: das tatsächlich Wirkende.
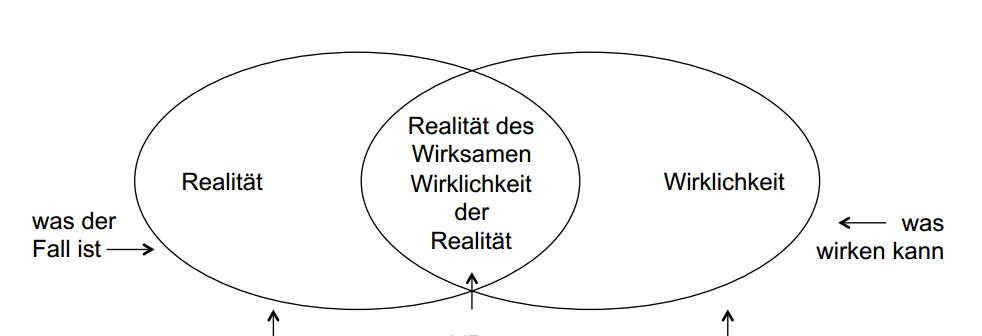
Quelle: Christoph Hubig, FG Philosophie der wissenschaftlich-technischen Kultur
Erkenntnis liefert kein Bild der wirklichen Welt, sondern nur eine subjektive Konstruktion, die zur Welt "passt" (wie ein Schlüssel zum Schloss passt).
Beispiele dafür, dass die Realität — als ein durch unser Gehirn gemaltes Bild der Wirklichkeit — hin und wieder ganz schön weit vom Wirklichen entfernt sein kann, finden sich im Video Realität ist oft nur Illusion.
Realität entsteht durch erst I n t e r p r e t a t i o n und dann E x t r a p o l a t i o n von Information,
die unsere Sinne empfangen und dem Gehirn zuleiten.
Sie ist nicht selten stark subjektiv geprägt, da wir oft nur erkennen, was wir erwarten.
Man kann es auch so ausdrücken:
Aller Sinn, den wir der Welt unterstellen, entsteht in uns selbst.
Die Wirklichkeit ist wie eine weiße Leinwand.
Wir bemalen sie selbst, und das so entstandene Bild ist die Realität, in der wir leben.
Und so hält jeder Mensch die Realität, in der er und andere leben, für am genauesten beschrieben durch
die Menge aller Aussagen, welche er selbst als wahr erachtet.
Warnung:
Leider benutzen selbst Wissenschaftler ein und dieselben Begriffe nicht immer in ein und derselben Bedeutung. Und so kommt es, dass, was oben » Realität « bzw. » Wirklichkeit « genannt wird, von Helmut Hille als » geistige Wirklichkeit « bzw. » außergeistige Realität « bezeichnet wird.
Selbst Philosophen (z.B. hier) verwenden oft das Wort "Wirklichkeit", wo sie über Realität sprechen. Das kann, wie etwa bei Markus Gabriel, recht verwirrend sein.
Solch unterschiedlicher Sprachgebrauch hat zur Folge, dass man schon wirklich sehr genau zuhören muss, um zu wissen, was Anton Zeilinger meint, wenn er sagt, Wirklichkeit und Information seien dasselbe, es sei aber Wirklichkeit doch nicht einfach n u r Information [siehe die Diskussion im Video "Information und Wirklichkeit" ab Minute 31:00 bis zum Schluss].
Insbesondere ist nicht klar, ob Helmut Hille Zeilinger richtig versteht.
Zeilinger jedenfalls denkt wie Niels Bohr, der ebenfalls unterschied zwischen
Interessante Ergänzung:
Was für eine Person zur Realität wird, lässt sich sogar manipulieren. Dies zeigt ein Ergebnis Schweizer Neurologen aus 2002: Sie konnten bei einer Patientin gezielt sog. Out-of-Body-Erfahrungen hervorgerufen.
Hier noch eine ganz besonders interessante Frage:
Ist Geist der Wirklichkeit zuzurechnen?
Wenn Biologen — oder gelegentlich auch Quantenphysiker — von » Geist « sprechen, meinen sie damit etwas, das es definitiv gibt, das aber doch durch keinerlei Messgerät erfasst werden kann. Hieraus folgt: Auch Geist könnte einfach nur etwas durch unseren Verstand Konstruiertes sein.
Mathematische Gesetzmäßigkeiten aber sind eindeutig der W i r k l i c h k e i t (und NUR ihr) zuzuordnen: Sie nämlich existierten schon lange bevor es in unserem Universum Menschen oder andere biologische Wesen gab.
Alles Existierende scheint letztlich Energie in unterschiedlichster Form zu sein, diese Form allerdings wandelt sich — gesteuert durch mathematische Gesetze — ständig (ebenso wie die Form der Wellen im Ozean sich ständig wandelt).
FRAGE also: Besteht Wirklichkeit vielleicht NUR aus Energie und mathematischen Gesetzen?
Görnitz argumentiert: Alles Reale ist einfach nur Bedeutung. Die Wirklichkeit ist Geist.
Quantenphysiker sagen gelegentlich, alles in der Welt sei durch Information — durch Form erzwingende Information mathematischer Art — gesteuerte Energie. Die Form aber ist ständig im Fluss.
Wäre Geist der Wirklichkeit zuzurechnen, könnte auch Energie nur Realität sein.
Im umgekehrten Fall aber wäre Geist nur Teil unseres Bildes der Wirklichkeit, der Energie also.
Das wiederum kann man nicht so recht glauben, obgleich es doch so scheint, als ob Bewusstsein – von Geist kaum zu unterscheiden – aus Energie emergiert.
Auf jeden Fall ist erstaunlich, wie Physiker und Philosophen nun schon 2600 Jahre lang
ständig neu zum selben Ergebnis kommen:
Mehr zu Kants Philosophe ...
Und hier der Grund, warum wir recht oft zu unterschiedlicher Meinung kommen:
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Lange vor Kant und Bohr vertrat diese Meinung auch schon Parmenides (geboren um 530 v.Chr.). Er schrieb:
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Schon Platons Höhlengleichnis hat versucht, zu erklären:
Erst Wirklichkeit ist das objektiv Vorhandene: das tatsächlich Wirkende.

Quelle: Christoph Hubig, FG Philosophie der wissenschaftlich-technischen Kultur
Erkenntnis liefert kein Bild der wirklichen Welt, sondern nur eine subjektive Konstruktion, die zur Welt "passt" (wie ein Schlüssel zum Schloss passt).
Beispiele dafür, dass die Realität — als ein durch unser Gehirn gemaltes Bild der Wirklichkeit — hin und wieder ganz schön weit vom Wirklichen entfernt sein kann, finden sich im Video Realität ist oft nur Illusion.
die unsere Sinne empfangen und dem Gehirn zuleiten.
Sie ist nicht selten stark subjektiv geprägt, da wir oft nur erkennen, was wir erwarten.
Man kann es auch so ausdrücken:
Aller Sinn, den wir der Welt unterstellen, entsteht in uns selbst.
Die Wirklichkeit ist wie eine weiße Leinwand.
Wir bemalen sie selbst, und das so entstandene Bild ist die Realität, in der wir leben.
Und so hält jeder Mensch die Realität, in der er und andere leben, für am genauesten beschrieben durch
die Menge aller Aussagen, welche er selbst als wahr erachtet.
Warnung:
Leider benutzen selbst Wissenschaftler ein und dieselben Begriffe nicht immer in ein und derselben Bedeutung. Und so kommt es, dass, was oben » Realität « bzw. » Wirklichkeit « genannt wird, von Helmut Hille als » geistige Wirklichkeit « bzw. » außergeistige Realität « bezeichnet wird.
Selbst Philosophen (z.B. hier) verwenden oft das Wort "Wirklichkeit", wo sie über Realität sprechen. Das kann, wie etwa bei Markus Gabriel, recht verwirrend sein.
Solch unterschiedlicher Sprachgebrauch hat zur Folge, dass man schon wirklich sehr genau zuhören muss, um zu wissen, was Anton Zeilinger meint, wenn er sagt, Wirklichkeit und Information seien dasselbe, es sei aber Wirklichkeit doch nicht einfach n u r Information [siehe die Diskussion im Video "Information und Wirklichkeit" ab Minute 31:00 bis zum Schluss].
Insbesondere ist nicht klar, ob Helmut Hille Zeilinger richtig versteht.
Zeilinger jedenfalls denkt wie Niels Bohr, der ebenfalls unterschied zwischen
- dem, was die Natur ist (und wie sie funktioniert)
- dem, wie sie sich uns zeigt (Information im Sinne Zeilingers) und
- dem, was unser Gehirn aus dieser Information macht: Unsere Realität.
Interessante Ergänzung:
Was für eine Person zur Realität wird, lässt sich sogar manipulieren. Dies zeigt ein Ergebnis Schweizer Neurologen aus 2002: Sie konnten bei einer Patientin gezielt sog. Out-of-Body-Erfahrungen hervorgerufen.
Hier noch eine ganz besonders interessante Frage:
Wenn Biologen — oder gelegentlich auch Quantenphysiker — von » Geist « sprechen, meinen sie damit etwas, das es definitiv gibt, das aber doch durch keinerlei Messgerät erfasst werden kann. Hieraus folgt: Auch Geist könnte einfach nur etwas durch unseren Verstand Konstruiertes sein.
Mathematische Gesetzmäßigkeiten aber sind eindeutig der W i r k l i c h k e i t (und NUR ihr) zuzuordnen: Sie nämlich existierten schon lange bevor es in unserem Universum Menschen oder andere biologische Wesen gab.
Alles Existierende scheint letztlich Energie in unterschiedlichster Form zu sein, diese Form allerdings wandelt sich — gesteuert durch mathematische Gesetze — ständig (ebenso wie die Form der Wellen im Ozean sich ständig wandelt).
FRAGE also: Besteht Wirklichkeit vielleicht NUR aus Energie und mathematischen Gesetzen?
Görnitz argumentiert: Alles Reale ist einfach nur Bedeutung. Die Wirklichkeit ist Geist.
Quantenphysiker sagen gelegentlich, alles in der Welt sei durch Information — durch Form erzwingende Information mathematischer Art — gesteuerte Energie. Die Form aber ist ständig im Fluss.
Im umgekehrten Fall aber wäre Geist nur Teil unseres Bildes der Wirklichkeit, der Energie also.
Das wiederum kann man nicht so recht glauben, obgleich es doch so scheint, als ob Bewusstsein – von Geist kaum zu unterscheiden – aus Energie emergiert.
ständig neu zum selben Ergebnis kommen:
Zitat von N. Bohr:
Die Physik kann nicht ergründen, wie die Natur funktioniert.
Aufgabe der Physik ist lediglich, zu untersuchen, wie die Natur sich uns zeigt.
Zitat von I. Kant:Es gibt die Dinge der Erscheinungen und die Dinge an sich.
Wir kennen die Dinge nur so, wie sie auf uns wirken.
Mehr zu Kants Philosophe ...
Und hier der Grund, warum wir recht oft zu unterschiedlicher Meinung kommen:
Zitat von Nietsche:
Jedes Sehen ist perspektivisches Sehen.
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Lange vor Kant und Bohr vertrat diese Meinung auch schon Parmenides (geboren um 530 v.Chr.). Er schrieb:
Zitat von Parmenides:
Die Welt, in der wir zu leben glauben, ist die vermeintliche Welt der Sinneswahrnehmungen;
die Welt ist nur Meinung ...
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Steven Hawking (1993):
Es hat keinen Zweck, sich auf die Wirklichkeit zu berufen, da wir kein modellunabhängiges Konzept der Wirklichkeit besitzen.
Nach meiner Meinung ist der unausgesprochene Glaube an eine modellunabhängige Wirklichkeit der tiefere Grund für die Schwierigkeiten, die Wissenschaftsphilosophen mit der Quantenmechanik und dem Unbestimmtheitsprinzip haben.
Quelle: Mein Standpunkt
|
Ich nehme den positivistischen Standpunkt ein, daß eine physikalische Theorie nur ein mathematisches Modell darstellt und daß es nicht sinnvoll ist, zu fragen, ob dieses der Realität entspricht. Man kann nur fragen, ob seine Vorhersagen mit den Beobachtungen in Einklang stehen.
Beitrag 0-532
Lebewesen sind — noch unvollkommene — Sinnesorgane der Wirklichkeit
Lebewesen sind Sinnesorgane der Wirklichkeit,
mit denen sie sich selbst beobachtet
wie durch winzige schmutzige Fensterscheiben
Das einzige, von dem wir wissen können, dass es existiert — da wir ja damit umgehen — ist unsere Vorstellung von Wirklichkeit.
Ob diese Vorstellung nun aber uns selbst oder anderes so zeigt, wie wir oder es tatsächlich sind, ist keineswegs garantiert.
Jedes Lebewesen (jedes Gehirn) ist sozusagen Sinnesorgan der Wirklichkeit, mit dessen Hilfe sie sich selbst — in jeweils nur kleinen Ausschnitten — wahrnimmt.
Fazit also:
Wir kennen die Welt nur über gedankliche Modelle, die wir selbst uns von ihr machen.
mit denen sie sich selbst beobachtet
wie durch winzige schmutzige Fensterscheiben
Das einzige, von dem wir wissen können, dass es existiert — da wir ja damit umgehen — ist unsere Vorstellung von Wirklichkeit.
Ob diese Vorstellung nun aber uns selbst oder anderes so zeigt, wie wir oder es tatsächlich sind, ist keineswegs garantiert.
Jedes Lebewesen (jedes Gehirn) ist sozusagen Sinnesorgan der Wirklichkeit, mit dessen Hilfe sie sich selbst — in jeweils nur kleinen Ausschnitten — wahrnimmt.
Etwas wahrzunehmen aber bedeutet, von ihm ausgesandte Signale zu empfangen und zu interpretieren.
Wie zutreffend diese Interpretation ist, bleibt offen, wird aber mindestens davon abhängig sein, wie viele der ausgesandten Signale ein Sinnesorgan tatsächlich erreichen und von ihm zur Kenntnis genommen werden können: Meist ist das zur Kenntnis Genommene nur kleiner Prozentsatz aller tatsächlich ausgesandten Signale, so dass jedes Bild B(G), das ein Gehirn G sich von Teilen T der Wirklichkeit macht, immer nur grob zutreffend sein kann.
Das gilt auch, wenn G selbst Teil von T ist (ein Lebewesen sich also selbst beobachtet).
Hinzu kommt noch, dass nicht alle Gehirne gleich gut darin sind, empfangene Signale zutreffend genug zu interpretieren.
Fazit also:
Hawking schrieb: Wir haben kein modellunabhängiges Verständnis der Wirklichkeit.
Er hat recht: Für uns existiert alles nur in Form der gedanklichen Modelle, welche Signalinterpretation uns nahe legt. Konkreter als diese gedanklichen Bilder existiert nur der Absender der Signale: eine uns unbekannte Wirklichkeit, von der wir einzig und allein wissen, dass wir selbst Teil davon sind und das einschließlich all unserer — nicht selten widersprüchlichen — Vorstellungen von ihr: Bilder, wie sie entstehen, da wir uns und unsere Umgebung nur an Hand unserer noch recht unvollkommenen Sinne (verschmutzten Spiegeln vergleichbar) betrachten und beobachten können.
Diese Einsicht ist genau das Gegenteil von dem, was Markus Gabriel uns weis zu machen versucht in seinem Buch » Warum es die Welt nicht gibt (2013) «.
Beitrag 0-437
Definition von: Leben, Wirklichkeit und Realität
Definition von
Leben, Wirklichkeit und Realität
Unter Berücksichtigung von dem, was in den Notizen [Realismus] und [Information] gesagt wird, erscheint es sinnvoll zu definieren:
Wie Einsteins Relativitätstheorie uns klar macht, ist
— der Endlichkeit der Lichtgeschwindigkeit wegen —
W(L,Z) Funktion des Ortes, an dem L sich zum Zeitpunkt Z befindet.
Leben, Wirklichkeit und Realität
Unter Berücksichtigung von dem, was in den Notizen [Realismus] und [Information] gesagt wird, erscheint es sinnvoll zu definieren:
- Leben ist, was die Fähigkeit hat, seiner Wirklichkeit Bedeutung zuzuordnen.
- Die Wirklichkeit W(L,Z) eines Lebewesens L zum Zeitpunkt Z ist alles, was sich L spätestens zum Zeitpunkt Z bekannt gemacht haben kann. Es ist dies die Summe aller Signale, die L spätestens zum Zeitpunkt Z erreicht haben können.
- Die Realität R(L,Z), in der ein Lebewesen zum Zeitpunkt Z lebt, ist seine — mehr oder weniger subjektive — Interpretation der Summe aller Signale, die L spätestens zum Zeitpunkt Z tatsächlich erreicht haben.
Wie Einsteins Relativitätstheorie uns klar macht, ist
— der Endlichkeit der Lichtgeschwindigkeit wegen —
W(L,Z) Funktion des Ortes, an dem L sich zum Zeitpunkt Z befindet.
Beitrag 0-451
Metaphysik und Philosophie
Metaphysik als Philosophie
Metaphysik kann man als den Versuch definieren, eine Theorie des Weltganzen zu entwickeln. Sie soll beschreiben, wie die Welt wirklich ist (im Gegensatz dazu, wie sie uns vorkommt).
Auf diese Weise — so schreibt Markus Gabriel — habe die Metaphysik die Welt gewissermaßen erst erfunden: Wir meinen damit alles, was wirklich der Fall ist: die Wirklichkeit.
Um herauszufinden, wie die Welt wirklich ist, muss man alles Menschengemachte davon abziehen (es also zunächst mal identifizieren).
Die Postmoderne — die Markus Gabriel jetzt durch das Zeitalter des Neuen Realismus zu ersetzen gedenkt — hat den Standpunkt vertreten, dass es die Dinge nur gibt, wie sie uns erscheinen. Dahinter, so argumentiert sie, gäbe es nichts mehr: keine Wirklichkeit.
Die Postmoderne, so Gabriel, sei eine Variante der Metaphysik und als solche nur eine besonders allgemeine Form des Konstruktivismus.
Der Konstruktivismus nämliche basiert auf der Annahme, dass es überhaupt keine Tatsachen an sich gäbe, da wir sie als Tatsachen einfach nur durch unsere vielfältigen Diskurse (auch die wissenschaftlicher Art) konstruieren.
Wichtiger Gewährsmann dieser nun schon 2500 Jahre alten Denktradition ist Immanuel Kant. Er behauptet, dass wir die Welt, wie sie wirklich ist, nicht erkennen können: Was auch immer wir erkennen, sei irgendwie auch von Menschen gemacht.
Quelle: Markus Gabriel: Warum es die Welt nicht gibt, Ullstein 2013, S. 10-11
Metaphysik kann man als den Versuch definieren, eine Theorie des Weltganzen zu entwickeln. Sie soll beschreiben, wie die Welt wirklich ist (im Gegensatz dazu, wie sie uns vorkommt).
Auf diese Weise — so schreibt Markus Gabriel — habe die Metaphysik die Welt gewissermaßen erst erfunden: Wir meinen damit alles, was wirklich der Fall ist: die Wirklichkeit.
Um herauszufinden, wie die Welt wirklich ist, muss man alles Menschengemachte davon abziehen (es also zunächst mal identifizieren).
Die Postmoderne — die Markus Gabriel jetzt durch das Zeitalter des Neuen Realismus zu ersetzen gedenkt — hat den Standpunkt vertreten, dass es die Dinge nur gibt, wie sie uns erscheinen. Dahinter, so argumentiert sie, gäbe es nichts mehr: keine Wirklichkeit.
Die Postmoderne, so Gabriel, sei eine Variante der Metaphysik und als solche nur eine besonders allgemeine Form des Konstruktivismus.
Der Konstruktivismus nämliche basiert auf der Annahme, dass es überhaupt keine Tatsachen an sich gäbe, da wir sie als Tatsachen einfach nur durch unsere vielfältigen Diskurse (auch die wissenschaftlicher Art) konstruieren.
Wichtiger Gewährsmann dieser nun schon 2500 Jahre alten Denktradition ist Immanuel Kant. Er behauptet, dass wir die Welt, wie sie wirklich ist, nicht erkennen können: Was auch immer wir erkennen, sei irgendwie auch von Menschen gemacht.
Beitrag 0-429
Zur wahren Natur der Realität, in der wir leben
Zur Natur der Realität, in der wir leben
Die Realität, in der ein Mensch lebt, ist nichts anderes als die Summe aller Bedeutung, die sein Gehirn Nachrichten zuordnet, die ihm zugestellt werden.
Das Interessante dabei ist:
Damit ist die Realität, in der ein Mensch lebt, nicht nur durch die Wirklichkeit bestimmt, sondern stets auch mit geprägt durch Gehirne, die nicht sein eigenes sind:
Die Realität, in der wir leben, gleicht demnach einem Ameisenhaufen, der ja auch nicht das Werk einer einzelnen Ameise ist, sondern das Werk der Gemeinschaft aller Ameisen, mit denen sie zusammenlebt.
Warum wird dann Rupert Sheldrake so stark angefeindet, wenn er die Frage in den Raum stellt, ob es nicht ein kollektives Gedächtnis gibt und unsere Gehirne lediglich die Werkzeuge sind, mit denen es aufgebaut, verwaltet, befragt und über den Tod einzelner Gehirne hinaus existent erhalten wird?
Die Realität, in der ein Mensch lebt, ist nichts anderes als die Summe aller Bedeutung, die sein Gehirn Nachrichten zuordnet, die ihm zugestellt werden.
Das Interessante dabei ist:
- Nachrichten entstehen als Nachrichten der Wirklichkeit (d.h. als abstrakte Information),
- wurden dann aber — auf dem Weg hin zu unserem Gehirn — oft schon durch viele andere Gehirne vorinterpretiert ( und teilweise auch uminterpretiert ).
Damit ist die Realität, in der ein Mensch lebt, nicht nur durch die Wirklichkeit bestimmt, sondern stets auch mit geprägt durch Gehirne, die nicht sein eigenes sind:
Die Realität, in der wir leben, gleicht demnach einem Ameisenhaufen, der ja auch nicht das Werk einer einzelnen Ameise ist, sondern das Werk der Gemeinschaft aller Ameisen, mit denen sie zusammenlebt.
Warum wird dann Rupert Sheldrake so stark angefeindet, wenn er die Frage in den Raum stellt, ob es nicht ein kollektives Gedächtnis gibt und unsere Gehirne lediglich die Werkzeuge sind, mit denen es aufgebaut, verwaltet, befragt und über den Tod einzelner Gehirne hinaus existent erhalten wird?
Beitrag 0-448
Realität ist die Sprache, in der wir die Natur befragen
Realität — konstruiert durch unser Denken — ist die Sprache,
in der wir die Natur befragen
Quelle: Ilya Prigogine, Isabelle Stengers: Dialog mit der Natur —
Neue Wege naturwissenschaftlichen Denkens, Serie Piper, S. 93-96
in der wir die Natur befragen
Ilya Prigogine (1980, 1986):
Es muss unterschieden werden zwischen
- den unmittelbaren Eindrücken, die wir von der Außenwelt empfangen, und
- der objektiven, » rationalen « Erkenntnis.
Letztere ist nicht passiv: Sie schafft sich ihre Gegenstände.
Wenn wir ein Phänomen zum Gegenstand der Erfahrung machen, nehmen wir a priori vor jeder wirklichen Erfahrung an, dass es einer Reihe von Prinzipien gehorcht (z.B. denen, die wir als Naturgesetze sehen).
Insofern das Phänomen als möglicher Erkenntnisgegenstand wahrgenommen wird, ist es Produkt der synthetischen Tätigkeit unseres Geistes.
Wir sind vor den Gegenständen unserer Erkenntnis da, und der Wissenschaftler ist selbst Quelle der universellen Gesetze, die er in der Natur entdeckt.
Die Natur insgesamt wird zu Recht jenen Gesetzen unterworfen, welche Wissenschaftler in ihr entziffern.
Die Wissenschaft wird zwar nicht immer dieselbe Antwort, aber doch immer die gleiche Form der Antwort erhalten.
Beitrag 0-410
Wie weit kennen wir die Wirklichkeit?
Wie weit kennen wir die Wirklichkeit?
Realität ist meist nur etwas durch unseren Verstand Konstruiertes: etwas Subjektives, von dem wir nur g l a u b e n , es sei objektiv genau so vorhanden.
Erst Wirklichkeit ist das objektiv Vorhandene: das tatsächlich Wirkende.
Wahrscheinlich sind mathematische Wahrheiten der einzige Teil der Wirklichkeit, den wir — wenn auch nur teilweise — kennen.
Realität ist meist nur etwas durch unseren Verstand Konstruiertes: etwas Subjektives, von dem wir nur g l a u b e n , es sei objektiv genau so vorhanden.
Erst Wirklichkeit ist das objektiv Vorhandene: das tatsächlich Wirkende.
Beitrag 0-269
Beispiele für die Unwirklichkeit aller Realität
Beispiele für die Unwirklichkeit von Realität
Der Neurowissenschaftler Karl Pribram argumentierte so:
Die Erkenntnis, dass erst unser Gehirn Objekte konstruiert — im oben erklärten Sinne — verblasst neben einer Schlussfolgerung, die der Quantenphysiker Bohm gezogen hat: Er nämlich ist davon überzeugt, dass wir sogar Raum und Zeit konstruieren. Die Relativität beider scheint das zu bestätigen.
Quelle: M Talbot:
Das holographische Universum (1992), S. 65-66
Der Neurowissenschaftler Karl Pribram argumentierte so:
Pribram (1989):
Die wahrnehmbare Glätte feinen Porzellans und das Gefühl des Sandstrands unter unseren nackten Füßen entstehen ebenso wie Phantomschmerz.
Dies bedeutet aber nicht, dass es da draußen keine Porzellantassen oder Sandkörner gäbe. Es bedeutet nur, dass eine Porzellantasse unterschiedliche Wirklichkeitsaspekte hat:
- Gefiltert durch das "Linsensystem" unseres Gehirns manifestiert sie sich als Tasse.
- Könnten wir uns aber von diesem Linsensystem befreien, würden wir sie als Interferenzmuster wahrnehmen [ gegeben
als Summe aller Feldanregungen, die Elementarteilchen darstellen ].
Welche dieser beiden Gestalten ist real und welche nur Illusion? Für mich sind beide real oder, wenn Sie so wollen, keine von beiden.
Die Erkenntnis, dass erst unser Gehirn Objekte konstruiert — im oben erklärten Sinne — verblasst neben einer Schlussfolgerung, die der Quantenphysiker Bohm gezogen hat: Er nämlich ist davon überzeugt, dass wir sogar Raum und Zeit konstruieren. Die Relativität beider scheint das zu bestätigen.
Beitrag 0-483
Physikalischer Antirealismus, wie Bohr und Heisenberg ihn erklären
Antirealismus begründet durch
Bohr und Heisenberg
Bohrs Standpunkt war fast noch radikaler, denn im zufolge ...
Quelle: Lee Smolin: Quantenwelt, 2019, S. 135-136
basierend auf:
Werner Heisenberg: Das Naturbild der heutigen Physik, Rohwolt 1955, S. 12, 21
Niels Bohr (1934) zitiert nach Max Jammer aus: The Philosophy of Quantum Mechanics in Historical Perspective, John Wiley and Sons, 1974, S. 103
Bohr und Heisenberg
Werner Heisenberg (gekürzt, aber wörtlich, wo kursiv gedruckt):
... man kann gar nicht mehr vom Teilchen losgelöst vom Beobachtungsvorgang sprechen.
Das hat zur Folge, daß die Naturgesetze, die wir in der Quantentheorie mathematisch formulieren, nicht mehr von den Elementarteilchen handeln, sondern [nur] von unserer Kenntnis der Elemetarteilchen [ gemeint ist: von der Kenntnis ihrer durch uns beobachtbaren Reaktionen auf Messfragen ].
Die Frage, ob diese Teilchen » an sich « in Raum und Zeit existieren, kann deswegen in dieser Form gar nicht gestellt werden.
Wenn von einem Naturbild der exakten Naturwissenschaften in unserer Zeit gesprochen werden kann, so handelt es sich eigentlich nicht um ein Bild der Natur, sondern nur um ein Bild unserer Beziehungen zur Natur [ will heißen: unsere Schlussfolgerung daraus, wie die Natur auf durch unsere Messgeräte gestellte Fragen antwortet ].
... Die Naturwissenschaft steht nicht mehr als Beschauer vor der Natur, sondern erkennt sich selbst als Teil dieses Wechselspiels zwischen Mensch und Natur. ...
Verschiedene anschauliche Bilder, mit denen wir atomare Systeme beschreiben, sind zwar für bestimmte Experimente angemessen, aber schließen sich [ nicht selten ] doch gegenseitig aus. ...
Diese verschiedenen Bilder sind richtig, wenn man sie an der richtigen Stelle verwendet, aber sie widersprechen einander, und man bezeichnet sie daher als komplementär zu einander.
Bohrs Standpunkt war fast noch radikaler, denn im zufolge ...
Niels Bohr (gekürzt, aber wörtlich, wo kursiv gedruckt):
... kann unabhängige Wirklichkeit im gewöhnlichen physikalischen Sinne [...] weder den Phänomenen, noch den Beabachtungsmitteln zugeschrieben werden.
... Jede vollständige Erhellung ein und desselben Gegenstandes kann unterschiedliche Gesichtspunkte erfordern, welche eine einzige Beschreibung in Frage stellen.
basierend auf:
Werner Heisenberg: Das Naturbild der heutigen Physik, Rohwolt 1955, S. 12, 21
Niels Bohr (1934) zitiert nach Max Jammer aus: The Philosophy of Quantum Mechanics in Historical Perspective, John Wiley and Sons, 1974, S. 103
Beitrag 1896-52
Unsere Welt — auch die der Physik — ist nur unser Bild von der Wirklichkeit
Schon erstaunlich, wie Physiker und Philosphen zum selben Ergebnis kommen:
Mehr zu Kants Philosophe ...
Interessant auch: Weit vor den beiden vertrat diese Meinung auch schon Parmenides (geboren um 530 v.Chr.). Er schrieb:
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Schon erstaunlich, wie Physiker und Philosphen zum selben Ergebnis kommen:
Zitat von N. Bohr:
Die Physik kann nicht ergründen, wie die Natur funktioniert.
Aufgabe der Physik ist lediglich, zu untersuchen, wie die Natur sich uns zeigt.
Zitat von I. Kant:Es gibt die Dinge der Erscheinungen und die Dinge an sich.
Wir kennen die Dinge nur so, wie sie auf uns wirken.
Mehr zu Kants Philosophe ...
Interessant auch: Weit vor den beiden vertrat diese Meinung auch schon Parmenides (geboren um 530 v.Chr.). Er schrieb:
Zitat von Parmenides:
Die Welt, in der wir zu leben glauben, ist die vermeintliche Welt der Sinneswahrnehmungen;
die Welt ist nur Meinung ...
Und genau das bestätigt uns im 20. Jahrhundert die Quantenphysik.
Steven Hawking (1993):
Es hat keinen Zweck, sich auf die Wirklichkeit zu berufen, da wir kein modellunabhängiges Konzept der Wirklichkeit besitzen.
Nach meiner Meinung ist der unausgesprochene Glaube an eine modellunabhängige Wirklichkeit der tiefere Grund für die Schwierigkeiten, die Wissenschaftsphilosophen mit der Quantenmechanik und dem Unbestimmtheitsprinzip haben.
Quelle: Mein Standpunkt
Beitrag 0-21
Das Wesen physikalischer Realität
Zum Wesen physikalischer Realität
John Archibald Wheeler — ein besonders visionärer Vertreter der Theoretischen Physik im 20. Jahrhundert — war der Meinung, eines Tages würde sich die gesamte Physik in der Sprache der Information verstehen lassen.
Das durch ihn geprägte Schlagwort » It from Bit « steht für die Idee, dass jeder Gegenstand der physikalischen Welt an seiner Basis eine nicht-materielle Quelle und Erklärung hat. Was wir Realität nennen entstehe letztlich aus Ja-Nein-Fragen und dem Glauben an die Richtigkeit der von der Natur darauf erhaltenen Antworten.
Auf dieses Weise, so Wheeler, seien alle physikalischen Dinge ihrem Ursprung nach informationstheoretischer Art und das in einen partizipatorischen Universum (womit er eine Welt meint, die nicht nur uns hervorbringt und formt, sondern die umgekehrt auch wir hervorbringen und mit gestalten).
Anton Zeilinger — der mit Sicherheit erfolgreichste und produktivste Quantenphysiker der Gegenwart — konkretisiert diesen Gedanken, indem er sagt
» Jedes der elementarsten Systeme trägt genau ein Bit an Information «.
Mit anderen Worten:
Was wir als die reale Welt erleben, in der wir leben, ist nichts anderes als durch uns als wahr eingestufte Information.
Wir erhalten sie als
u n s e r e Interpretation von Nachrichten (= Bitfolgen),
deren jede die Natur uns als Antwort zustellt, wenn wir sie beobachten, d.h. ihr eine Ja-Nein-Frage stellen.
Jedes dieser Bits entsteht durch Kollabieren eines QuBits, so dass sein Wert sich zufällig,
aber doch unter Verträglichkeit mit gewissen Wahrscheinlichkeiten ergibt:
Zu Realität wird genau eine von zwei durch unsere Frage noch offen gelassener Möglichkeiten.
Man könnte es auch so sagen:
Was wir als Realität empfinden, ist eine Menge mit JA oder NEIN beantworteter Fragen.
John Archibald Wheeler — ein besonders visionärer Vertreter der Theoretischen Physik im 20. Jahrhundert — war der Meinung, eines Tages würde sich die gesamte Physik in der Sprache der Information verstehen lassen.
Das durch ihn geprägte Schlagwort » It from Bit « steht für die Idee, dass jeder Gegenstand der physikalischen Welt an seiner Basis eine nicht-materielle Quelle und Erklärung hat. Was wir Realität nennen entstehe letztlich aus Ja-Nein-Fragen und dem Glauben an die Richtigkeit der von der Natur darauf erhaltenen Antworten.
Auf dieses Weise, so Wheeler, seien alle physikalischen Dinge ihrem Ursprung nach informationstheoretischer Art und das in einen partizipatorischen Universum (womit er eine Welt meint, die nicht nur uns hervorbringt und formt, sondern die umgekehrt auch wir hervorbringen und mit gestalten).
Anton Zeilinger — der mit Sicherheit erfolgreichste und produktivste Quantenphysiker der Gegenwart — konkretisiert diesen Gedanken, indem er sagt
Mit anderen Worten:
Was wir als die reale Welt erleben, in der wir leben, ist nichts anderes als durch uns als wahr eingestufte Information.
Wir erhalten sie als
u n s e r e Interpretation von Nachrichten (= Bitfolgen),
deren jede die Natur uns als Antwort zustellt, wenn wir sie beobachten, d.h. ihr eine Ja-Nein-Frage stellen.
Jedes dieser Bits entsteht durch Kollabieren eines QuBits, so dass sein Wert sich zufällig,
aber doch unter Verträglichkeit mit gewissen Wahrscheinlichkeiten ergibt:
Zu Realität wird genau eine von zwei durch unsere Frage noch offen gelassener Möglichkeiten.
Man könnte es auch so sagen:
Der Quantenphysiker Hans-Peter Dürr schrieb:
Alles, was wir durch Beobachtungen oder durch Abstraktion unserer Wahrnehmungen als Wirklichkeit betrachten und in der Naturwissenschaft als (stoffliche) Realität beschreiben, darf in dieser Form nicht mit der eigentlichen Wirklichkeit gleichgesetzt werden.
Beitrag 0-37
Zeit, Mathematik und Realität
Zeit, Mathematik und Realität
Stueps liegt da aber falsch, denn ich — der ich ja Informatiker und Mathematiker bin — weiß, dass mathematische Gesetze uns Wirkliches beschreiben:
Wir sind gewohnt, durch sie beschriebene Wirklichkeit als Realität anzuerkennen ( wohingegen wir wissen, dass i.A. Reales eben n i c h t auch Wirkliches ist ).
Mein Verdacht:
Mathematische Gesetze könnten die einzigen Naturgesetze sein
( oder wenigstens die einzigen, die uns Wirkliches als Realität zu zeigen in der Lage sind ).
Harti in 2155-13
Hallo Okotombrok und Hans-m
Man kann natürlich den 2.Haupsatz der Thermodynamik (Entropiesatz) zum Inhalt des Begriffs der Zeit machen; dann hat die Zeit eine Richtung in dem Sinn, dass sie sich in Richtung Zunahme der Entropie bewegt. Dies ist aber nicht besonders praktisch und spielt wohl bei der Bestimmung von "vorher" (Vergangenheit) und "nachher" (Zukunft) normalerweise keine Rolle. "Vorher" und "Nachher" ( Richtung der Zeit) werden im allgemeinsprachlichen Verständnis allein durch die kausalen Geschehensabläufe bestimmt. Die Kindheit eines Menschen ist "vorher" und das Erwachsenenalter "nachher".
Die Vorstellung von Zeit hat sich derartig verselbständigt, dass uns nicht bewußt ist, dass wir Vergangenheit und Zukunft im Prinzip über kausales Geschehen definieren. Dies ist allgemeinsprachlich kein Problem, führt aber naturwissenschaftlich zu Verwunderung, indem man nicht versteht, warum die mathematisch formulierten Naturgesetze "zeitinvariant" sind. Die Zeit hat in diesen Naturgesetzen eben keine Richtung. Richtiger müsste es deshalb heißen:
Die Naturgesetze sind kausalitätsinvariant. Sie schließen z.B. prinzipiell nicht aus, dass die zerbrochene Tasse sich wieder zusammensetzt und auf den Tisch springt.
Kletzenbauer darauf in 2155-14
Eher ist die Mathematik kausalitätsinvariant und realitätsinvariant. Wenn sich nämlich in einem Raum 3 Leute aufhalten, und 5 Leute verlassen ihn, dann müssen 2 Leute reingehen, damit der Raum leer ist.
Stueps darauf in 2155-15
Mathematik hat mit Realität fast nichts zu tun. Das wird jeder Informatiker unterschreiben.
Stueps liegt da aber falsch, denn ich — der ich ja Informatiker und Mathematiker bin — weiß, dass mathematische Gesetze uns Wirkliches beschreiben:
Wir sind gewohnt, durch sie beschriebene Wirklichkeit als Realität anzuerkennen ( wohingegen wir wissen, dass i.A. Reales eben n i c h t auch Wirkliches ist ).
Mein Verdacht:
( oder wenigstens die einzigen, die uns Wirkliches als Realität zu zeigen in der Lage sind ).
Beitrag 0-528
Warum jeder eben doch nur in seiner eigenen Welt lebt
Wie sich Realitäten in uns unbekannte Wirklichkeit (den Kosmos) einbetten
Jedes denkende Wesen lebt in einem nicht allzu klaren, persönlichen Spigelbild eines kleinen Teiles der Wirklichkeit
Spiegel in diesem Sinne ist das Gehirn des Lebewsens
Wisse: Es gibt einen Unterschied zwischen Realität und Wirklichkeit:
Die Wirklichkeit kennen wir nur über von ihr erzeugte Signale, die unsere Sinne empfangen. Unser Gehirn erzeugt daraus unsere Vorstellung, wie die Wirklichkeit denn wohl sein müsse. Nennen wir es: Unser Modell der Wirklichkeit.
Man nennt es die Realität, in der wir leben. Wir synchronisieren es (teilweise) mit der Realität, in der andere leben, indem wir mit ihnen kommunizieren.
Hat man nun aber zwei biologische Wesen, Menschen etwa (oder z.B. einen Mensch und seinen Hund), so kann deren Modell der Wirklichkeit nicht genau das gleiche sein sein, da ihrer beider Sinne ja so gut wie nie genau dieselbe Menge von Signalen aufgefangen haben (und auch nicht alle Gehirne gleich leistungsfähig sind).
Da wir mit unserem jeweiligen gedanklichen Bild der Wirklichkeit nun aber selbst auch ein Teil der Wirklichkeit sind, ist jede Realität, in der einer von uns lebt, nur kleiner Teil der Wirklichkeit insgesamt: Unser oft subjektiv geprägtes Bild (= Verständnis) des Teiles der Wirklichkeit, der mit uns — direkt oder indirekt — kommuniziert. Empirie und alles rationale Denken eines Gehirns kann sich direkt stets nur auf eines dieser Modelle beziehen: auf das von diesem Gehirn selbst erzeugte.
Steven Hawking hat das so ausgedrückt:
Wir haben kein modellunabhängiges Verständnis der Wirklichkeit.
Konsequenz daraus:
Weite Teile der Wirklichkeit sind uns empirisch nicht einsehbar.
Über sie können wir nur spekulieren. Sie haben auf jeden Fall auch eine geistige Dimension.
Spiegel in diesem Sinne ist das Gehirn des Lebewsens
Wisse: Es gibt einen Unterschied zwischen Realität und Wirklichkeit:
Die Wirklichkeit kennen wir nur über von ihr erzeugte Signale, die unsere Sinne empfangen. Unser Gehirn erzeugt daraus unsere Vorstellung, wie die Wirklichkeit denn wohl sein müsse. Nennen wir es: Unser Modell der Wirklichkeit.
Man nennt es die Realität, in der wir leben. Wir synchronisieren es (teilweise) mit der Realität, in der andere leben, indem wir mit ihnen kommunizieren.
Hat man nun aber zwei biologische Wesen, Menschen etwa (oder z.B. einen Mensch und seinen Hund), so kann deren Modell der Wirklichkeit nicht genau das gleiche sein sein, da ihrer beider Sinne ja so gut wie nie genau dieselbe Menge von Signalen aufgefangen haben (und auch nicht alle Gehirne gleich leistungsfähig sind).
Da wir mit unserem jeweiligen gedanklichen Bild der Wirklichkeit nun aber selbst auch ein Teil der Wirklichkeit sind, ist jede Realität, in der einer von uns lebt, nur kleiner Teil der Wirklichkeit insgesamt: Unser oft subjektiv geprägtes Bild (= Verständnis) des Teiles der Wirklichkeit, der mit uns — direkt oder indirekt — kommuniziert. Empirie und alles rationale Denken eines Gehirns kann sich direkt stets nur auf eines dieser Modelle beziehen: auf das von diesem Gehirn selbst erzeugte.
Steven Hawking hat das so ausgedrückt:
Konsequenz daraus:
Über sie können wir nur spekulieren. Sie haben auf jeden Fall auch eine geistige Dimension.
Beitrag 0-5
Es gibt mathematischen, aber sicher keinen physikalischen Realismus
Quelle: Rebecca Goldsteins Gödel-Biographie ( Piper Taschenbuch 2005, S. 43-46 )
Es gibt keinen physikalischen Realismus (!)
Dass zu dieser Überzeugung zunächst Parmenides, später aber auch Kant und Niels Bohr kamen, wusste ich. Gerade eben aber lese ich bei Josef Honerkamp, dass es auch auch Hawking so sieht und Honerkamp — selbst ein Physiker — derselben Meinung ist:
Note: Honerkamp ist emeritierter Professor für Theoretische Physik und Autor einiger sehr lesenswerter Bücher.
Für jeden verständlich ist mindestens Die Entdeckung des Unvorstellbaren: Einblicke in die Physik und ihre Methode (2010).
Rebecca Goldstein
Gödels Auffassung, dass die mathematische Wirklichkeit objektiv existiert, wird als Begriffsrealismus, als
Mathematischer Realismus
oder mathematischer Platonismus bezeichnet.
Viele Mathematiker sind mathematische Realisten gewesen, und selbst jene, die sich nicht als solche bezeichnen, bekennen sich implizit zum Realismus, indem sie ihre Arbeiten als » Entdeckungen « beschreiben.
Der hoch angesehene Mathematiker G.H. Hardy (1877-1947) formulierte seine platonische Überzeugung in seinem Klassiker A Mathematician's Apology sehr deutlich so:
G.H. Hardy
Ich glaube, dass die methematische Wirklichkeit außerhalb unseres Geistes existiert, dass es unsere Aufgabe ist, sie zu entdecken bzw. zu beobachten, und dass die Theoreme, die wir beweisen und hochtrabend unsere » Entdeckungen « nennen, schlicht Aufzeichnungen unserer Beobachtungen sind. ...
Diese realistische Anschauung ist für die mathematische Wirklichkeit viel plausibler als für die physikalische, da bei mathematischen Objekten Schein und Sein weitgehend zusammenfallen:
- Ein Stuhl oder ein Stern sind nicht im mindesten, was sie zu sein scheinen: Je gründlicher wir darüber nachdenken, um so verschwommener werden ihre Konturen im Dunstschleier der Sinnesempfindungen, der sie einhüllt.
- Aber » 2 « oder » 317 « haben nichts mit Empfindungen zu tun; Ihre Eigenschaften treten um so deutlicher hervor, je gründlicher wir sie untersuchen. 317 ist eine Primzahl, nicht weil wir das meinen oder weil dies den Strukturen unseres Denkens entspräche, sondern weil es so ist, weil mathematische Wirklichkeit nun einmal so beschaffen ist.
Ein Mathematiker nach dem anderen hat — wie Hardy — seine platonische Auffassung bekräftigt, wonach mathematische Wahrheiten entdeckt und nicht erfunden werden ...
Gödels metamathematische Anschauung, sein fester Glaube an die objektive, vom menschlichen Denken unabhängige Existenz der mathematischen Wirklichkeit, stellt vielleicht die Qintessenz seine Lebenswerkes dar ...
Dass zu dieser Überzeugung zunächst Parmenides, später aber auch Kant und Niels Bohr kamen, wusste ich. Gerade eben aber lese ich bei Josef Honerkamp, dass es auch auch Hawking so sieht und Honerkamp — selbst ein Physiker — derselben Meinung ist:
Honerkamp (2010)
Ein wichtiger Punkt, den Hawking in aller Klarheit betont, ist der, dass es seiner Meinung nach keinen theorieunabhängigen Realitätsbegriff gibt.
Diese Aussage beschreibt genau das, was Physiker im Umgang mit den physikalischen Theorien immer wieder erfahren.
Für jeden verständlich ist mindestens Die Entdeckung des Unvorstellbaren: Einblicke in die Physik und ihre Methode (2010).
Beitrag 0-424
Wie sich Realität von Wirklichkeit unterscheidet — 2 Beispiele
Die Realität, in der wir leben ...
... ist die Summe aller Bedeutung, die wir Signalen zuordnen, die uns erreichen.
Wie wenig wir in wirklicher Welt leben zeigen folgende Beobachtungen:
... ist die Summe aller Bedeutung, die wir Signalen zuordnen, die uns erreichen.
Wie wenig wir in wirklicher Welt leben zeigen folgende Beobachtungen:
- Farbe das beste Beispiel dafür, dass wir die Welt eben NICHT so wahrnehmen, wie sie ist:
Was unser Auge erreicht, ist elektromagnetische Strahlung gewisser Wellenlänge.
Erst unser Gehirn setzt die ankommende Wellenlänge um in einen Farbeindruck.
- Materie das andere wichtige Beispiel: Wie die Quantenphysik zeigt, existiert z.B. jeder Stein (und auch jeder Beobachter des Steins) physisch nur als unglaublich kompliziertes Paket harmonischer Wellen im Feld der physikalischen Grundkräfte.
Hans Peter Dürr hat das auf den Punkt gebracht, indem er schrieb:
-
Ich habe als Physiker 50 Jahre lang — mein ganzes Forscherleben — damit verbracht zu fragen, was eigentlich hinter der Materie steckt.
Des Endergebnis ist ganz einfach:
Es gibt keine Materie!
Gemeint damit hat er natürlich:
Was ihr als Materie wahrzunehmen glaubt, ist etwas ganz anderes, als ihr denkt:
Jedes Stück Materie ist einfach nur ein hoch kompliziertes Feld physikalischer Kräfte.
Lies mehr dazu in: Warum Hans-Peter Dürr zu Unrecht der Esoterik verdächtigt wurde.
Beitrag 1057-142
Eine treffende Feststellung — sollte man sich merken
Hi Harti,
das finde ich sehr treffend - muss ich mir merken.
Danke, grtgrt
Harti aus 1057-136:Grtgrt aus 1057-123:Mir legt das den Verdacht nahe, dass die Natur die Begriffe unvorstellbar klein und unvorstellbar groß irgendwie als gleichwertig betrachtet.
Hallo Grtgrt,
ich bin der Meinung, dass der Gegensatz klein-groß eine Folge unserer Methode zur Erfassung der Natur ist und keine Eigenschaft von Objekten.
Hi Harti,
das finde ich sehr treffend - muss ich mir merken.
Danke, grtgrt
Beitrag 1057-192
Mathematische Konstanten existieren in nur einer Version
Hallo H...,
Pi ist ein reiner Quotient und keine Größe. Dieser Quotient ist unabhängig vom Zahlensystem immer der gleiche. Der Umfang ist immer etwa dreimal so groß wie der Durchmesser eines Kreises.
Was meinst du mit "einer anderen Mathematik" bei der der Umfang nicht ca. dreimal so groß sein sollte?
Du verwechselst reine Zahlenbeträge, die sicher abhängig sind von willkürlich gewählten physikalischen Einheiten, mit den Verhältnissen in der Natur.
Ich weiß nicht, von welchen theoretischen Überlegungen du sprichst und vielleicht verrätst du es uns ja noch. Du wirst doch wohl nicht lediglich von Einheitensystemen reden? Derer gibt es mehrere, praktische und weniger praktische. Das wäre nun wirklich trivial und keiner theoretischen Überlegung wert. Das Wirkungsquantum ist davon wohl kaum abhängig, genausowenig wie von der Mathematik, ob unsere oder irgendeiner "anderen Mathematik", von der du sprichst.
mfg okotombrok�
H... aus 1057-191:Ich glaube, die Größe π, die du hier ansprichst, ist nicht wesentlich. Bei einer anderen Mathematik wäre der Wert anders (hier gab es historisch viele Versuche...).
Pi ist ein reiner Quotient und keine Größe. Dieser Quotient ist unabhängig vom Zahlensystem immer der gleiche. Der Umfang ist immer etwa dreimal so groß wie der Durchmesser eines Kreises.
Was meinst du mit "einer anderen Mathematik" bei der der Umfang nicht ca. dreimal so groß sein sollte?
Du verwechselst reine Zahlenbeträge, die sicher abhängig sind von willkürlich gewählten physikalischen Einheiten, mit den Verhältnissen in der Natur.
Zitat von H...:Es gibt theoretischen Überlegungen, wonach verschiedenen "Längenmessungen" existieren (und wir bisher immer nur eine davon anwenden) - und die sind völlig äquivalent. Das würde dazu führen, dass dein 2. Bsp. rein betragsmässig anders aussieht.
Ich weiß nicht, von welchen theoretischen Überlegungen du sprichst und vielleicht verrätst du es uns ja noch. Du wirst doch wohl nicht lediglich von Einheitensystemen reden? Derer gibt es mehrere, praktische und weniger praktische. Das wäre nun wirklich trivial und keiner theoretischen Überlegung wert. Das Wirkungsquantum ist davon wohl kaum abhängig, genausowenig wie von der Mathematik, ob unsere oder irgendeiner "anderen Mathematik", von der du sprichst.
mfg okotombrok�
Beitrag 949-64
Wichtige Details zur Kopenhagener Interpretation
An alle,
es mag ja sein, dass E... die Antwort ganz genau kennt, ich aber weiß nur folgendes:
Auf die Frage, wer Stapp denn nun eigentlich ist, bekommt man zur Antwort: "Stapp is a leading quantum physicist who has given particularly careful thought to the implications of the theory that lies at the heart of modern physics. In this book, which contains several of his key papers as well as new material, he focuses on the problem of consciousness and explains how quantum mechanics allows causally effective conscious thought to be combined in a natural way with the physical brain made of neurons and atoms."
Gruß, grtgrt
PS: Was ich an Schäfer so mag ist, dass seine Sprache ebenso klar ist, wie seine Gedanken.
E... aus 949-62:Wie soll ein makroskopisches System mit Bestandteilen funktionieren die quantenphysikalische Eigenschaften haben, nicht stabil, nicht fassbar, nicht berechenbar und zeitlos sind? Antworte bitte nicht auf die Frage ...
An alle,
es mag ja sein, dass E... die Antwort ganz genau kennt, ich aber weiß nur folgendes:
Zitat von Lothar Schäfer, Hochschullehrer:
Die Kopenhagener Interpretation betrachtet den Kollaps der Wellenfunktion in einem Messakt NICHT als plötzliche Änderung des Zustandes des Universums, sondern lediglich als plötzliche Änderung unseres Wissens um irgendein Phänomen der physikalischen Wirklichkeit.
Henry Stapp hat in seinem Buch "Mind, Matter, and Quantum Mechanics" (1993) diese Ansicht so charakterisiert: In der Kopenhagener Interpretation ist das wahre Wesen von ψ nicht ein Problem der Ontologie, sondern eines der Epistomologie.
Auf die Frage, wer Stapp denn nun eigentlich ist, bekommt man zur Antwort: "Stapp is a leading quantum physicist who has given particularly careful thought to the implications of the theory that lies at the heart of modern physics. In this book, which contains several of his key papers as well as new material, he focuses on the problem of consciousness and explains how quantum mechanics allows causally effective conscious thought to be combined in a natural way with the physical brain made of neurons and atoms."
Gruß, grtgrt
PS: Was ich an Schäfer so mag ist, dass seine Sprache ebenso klar ist, wie seine Gedanken.
Beitrag 1107-25
Beantworten wir Irenas Argumente
Hallo Irena,
da du mir so ausführlich geantwortet hast, will ich es auch tun. Also:
Ich behaupte ja gar nicht, dass der Denkfehler in der Selbstbezüglichkeit liegt — er liegt einfach nur darin, dass manche Leute (du etwa) nicht einsehen wollen, dass z.B. die Aussage "Diese Aussage ist falsch." einem logischen Gleichungssystem entspricht, welches KEINE Lösung hat. Paradox ist daran gar nix, denn die Mathematik kennt jede Menge von Gleichungssystemen, die keine Lösung haben.
Diese meine Aussage bezieht sich einfach nur auf die Tatsache, dass Mathematiker (Algebraiker z.B.) heutzutage fast jeden ihrer Beweis mit Hilfe naiver Mengenlehre formulieren, obgleich sie doch wissen, dass Russell gezeigt hat, dass naive Mengenlehre zu Widersprüchen führen kann (also nicht wirklich zuverlässig ist).
WARNUNG also: Wer naive Mengenlehre gebraucht, muss das hinreichend vorsichtig tun, also sicherstellen, dass jede Definition, die er mit ihrer Hilfe formuliert, auch wirklich Sinn macht (was manchmal selbst schon einen eigenen, komplizierten Beweis erfordern kann).
Du hast völlig recht: In der Mathematik (genauer: in mathematischen Gesetzmäßigkeiten) spiegelt sich physikalische Realität.
Mit irgendwelchen Messgrenzen aber hat das gar nichts zu tun (warum auch?).
Ich schätze Andre Weil sehr, da ich seine mathematischen Fähigkeiten wirklich bewundere.
Dennoch sollte er den Teufel besser nicht bemühen, denn Gödels Ergebnis ist letztlich nur Ausdruck der Tatsache, dass allein schon die natürlichen Zahlen uns in ganz unglaubliche mathematische Tiefen zu führen im Stande sind — in eine Welt, in die man ohne Ende immer tiefer gehen kann, ganz so wie man sich in eine Mandelbrotmenge ohne Ende immer tiefer hinein zoomen kann und dann dort eine schier unendliche Vielfalt von Formen und Farben entecken kann (siehe z.B. Abschnitt 1 bis 14 in Wikipedia). Die Menge aller Primzahlen z.B. ist ein Wunder für sich, und wir Menschen haben gerade erst begonnen, die allereinfachsten Strukturen dieser Menge zu verstehen ...
Leopold Kronecker (ein Zahlentheoretiker) hat mal voller Bewunderung gesagt:
Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
Da ist viel Wahres dran.
Wenn du denkst, ich würde irgendeinen Weltuntergang sehen, dann versteht du mich völlig falsch.
Ich bin aber sehr wohl der Ansicht, dass die Informatik — was erfolgreiche Qualitätssicherung ihrer Ergebnisse betrifft — der Mathematik um etwa 2 Jahrtausende hinterher hinkt. Nur darauf wollte ich hinweisen.
Ich bleibe bei meiner Meinung.
... und wer Andre Weils Buch " Basic Number Theory" wirklich durchgearbeitet hat, wird wissen, was ich meine (denn was er als einen schon hinreichend kleinen, überzeugenden Gedankensprung da so alles stehen lässt, kann schon mal ein bis zwei Stunden Arbeit kosten, es einzusehen. Einen Fehler aber konnten wir, die wir sein Buch damals im Detail durchgearbeitet haben, ihm aber wirklich NIEMALS nachweisen. Wie gesagt: Ich bewundere ihn ...
Dein erstes Argument scheint mir einfach nur ein Spiel mit Worten — es sagt rein gar nichts.
Zum zweiten: Wer etwas modelliert (mit oder ohne Mathematik) wird i.A. zu einem Modell kommen, welches irgendwo hinkt, und somit den zu modellierenden Gegenstand eben NICHT mehr in allen Einzelheiten korrekt abbildet. Das sehe ich als Selbstverständlichkeit — es ist sogar zwangsläufig so, denn ein Modell soll ja häufig auch vereinfachen (sich also auf nur bestimmte Aspekte konzentrieren).
Auch was du hier sagst, scheint mir nur ein Spiel mit Worten.
Dass mein Statement "... viele Ergebnisse indirekter Beweisführung schon ihrer Natur nach nicht Ergebnis rein konstruktiver Mathematik sein können" durchaus richtig ist, zeigt sich sehr schön in Beitrag 1107-22, wo wir im zweiten Kullerpunkt ja tatsächlich einen indirekten Beweis führen. Über rein konstruktive Mathematik wäre ganz sicher NICHT beweisbar, dass K lügt.
Ich habe keine Anhnung, wo da ein Zirkelschluss sein sollte.
Da bin ich völlig deiner Meinung:
Nachdem man indirekt bewiesene Wahrheiten nicht konstruieren kann, könnte man sich schon fragen, ob sie wirklich einen realen Teil der Natur darstellen.
Problem nur: Wie will man den Begriff real den nun wirklich genau definieren?
Schade, dass dir hier offenbar die Puste aus geht ...
Gruß, grtgrt
da du mir so ausführlich geantwortet hast, will ich es auch tun. Also:
Irena aus 1107-20:Hallo Doppel-grt,
ich denke, dass es gerade du muss über den Kopf gehen lassen, da das Problem der Selbstbezüglichkeit ist KEIN Denkfehler. Es ist objektive Gegebenheit. Du schreibst den Unvollständigkeit Satz zwar auf, dennoch ziehst von ihm keine Schlussfolgerung. Im Gegenteil, du läufst mit Flage, auf der "der Denkfehler" - also subjektive Gegebenheit - geschrieben ist.
Ich behaupte ja gar nicht, dass der Denkfehler in der Selbstbezüglichkeit liegt — er liegt einfach nur darin, dass manche Leute (du etwa) nicht einsehen wollen, dass z.B. die Aussage "Diese Aussage ist falsch." einem logischen Gleichungssystem entspricht, welches KEINE Lösung hat. Paradox ist daran gar nix, denn die Mathematik kennt jede Menge von Gleichungssystemen, die keine Lösung haben.
Irena aus 1107-20:Zitat von grtgrt:Das so zur Verlässlichkeit heute üblicher mathematischer Denkwerkzeuge!
So viel Emotionen!..
Ich sehe es überhaupt nicht so tragisch wie du. Mathematiker haben in Jahrtausenden ihre Gebäude gebildet und diese Gebäude sich als verlässlich aufweist. Deine Verallgemeinerung der Unzuverlässlichkeit der mathematischen Werkzeuge ist von dir stark übertrieben.
Diese meine Aussage bezieht sich einfach nur auf die Tatsache, dass Mathematiker (Algebraiker z.B.) heutzutage fast jeden ihrer Beweis mit Hilfe naiver Mengenlehre formulieren, obgleich sie doch wissen, dass Russell gezeigt hat, dass naive Mengenlehre zu Widersprüchen führen kann (also nicht wirklich zuverlässig ist).
WARNUNG also: Wer naive Mengenlehre gebraucht, muss das hinreichend vorsichtig tun, also sicherstellen, dass jede Definition, die er mit ihrer Hilfe formuliert, auch wirklich Sinn macht (was manchmal selbst schon einen eigenen, komplizierten Beweis erfordern kann).
Irena aus 1107-20:Für mich die Unvollständigkeitsätze von Gödel nur eines bedeuten, eben das, was ich schon vorher geschrieben habe: die Mathematik ist ein Medium, das physikalische Realität widerspiegelt. Ähnlich stoßt auch Physik an ihre Grenzen: der Messungsgrenzen, der Grenzen der physikalischen Realität.
Du hast völlig recht: In der Mathematik (genauer: in mathematischen Gesetzmäßigkeiten) spiegelt sich physikalische Realität.
Mit irgendwelchen Messgrenzen aber hat das gar nichts zu tun (warum auch?).
Irena aus 1107-20:Es ist ein schönes Satz von Andre Weil, der gesagt haben soll: "Gott existiert, weil Mathematik konsistent ist, und Teufel existiert, weil wir das nicht beweisen können".
Ich schätze Andre Weil sehr, da ich seine mathematischen Fähigkeiten wirklich bewundere.
Dennoch sollte er den Teufel besser nicht bemühen, denn Gödels Ergebnis ist letztlich nur Ausdruck der Tatsache, dass allein schon die natürlichen Zahlen uns in ganz unglaubliche mathematische Tiefen zu führen im Stande sind — in eine Welt, in die man ohne Ende immer tiefer gehen kann, ganz so wie man sich in eine Mandelbrotmenge ohne Ende immer tiefer hinein zoomen kann und dann dort eine schier unendliche Vielfalt von Formen und Farben entecken kann (siehe z.B. Abschnitt 1 bis 14 in Wikipedia). Die Menge aller Primzahlen z.B. ist ein Wunder für sich, und wir Menschen haben gerade erst begonnen, die allereinfachsten Strukturen dieser Menge zu verstehen ...
Leopold Kronecker (ein Zahlentheoretiker) hat mal voller Bewunderung gesagt:
Da ist viel Wahres dran.
Irena aus 1107-20:Zu der subjektiven Grundlage der Mathematik. Da wir obendrauf ein objektives Gebäude haben, dann wird wohl das Subjektive an das Objektive anpassen müssen. Daher hat das Subjektive auch nicht volle Freiheit. Oder wenn Mathematiker eigenen subjektiven Empfindungen nachgeht, kann er vielleicht ein anderes Gebäude nebenan schaffen. Auf die Weise mathematische "Stadt" nur gewinnt. Daher bitte hier keinen Weltuntergang sehen.
Wenn du denkst, ich würde irgendeinen Weltuntergang sehen, dann versteht du mich völlig falsch.
Ich bin aber sehr wohl der Ansicht, dass die Informatik — was erfolgreiche Qualitätssicherung ihrer Ergebnisse betrifft — der Mathematik um etwa 2 Jahrtausende hinterher hinkt. Nur darauf wollte ich hinweisen.
Irena aus 1107-20:Zitat:Mathematische Beweise im Bereich nicht konstruktiver Mathematik sind aber nur Zerlegung großer Gedankensprünge in zunehmend kleinere bis hin zu einem Punkt, an dem der Zuhörer der Mei¬nung ist, jeder dieser kleinen Gedankensprünge bedürfe keines Beweises mehr, sondern behaupte offensichtlich Wahres. Wo dieser Punkt erreicht ist, muss subjektiv entschieden werden und hängt sehr von der Vorbildung des Zuhörers ab sowie von seiner Kritikfähigkeit.
Ich denke, dass "wo dieser Punkt erreicht wird" hängt nicht von der Subjektiven. Du übersiehst nämlich, dass Mathematik ist s. z. gemeinschaftliches Produkt. Wie in jedem Gemeinschaftsprodukt, muss das Erreichte von einem durch anderen geprüft werden.
Ich bleibe bei meiner Meinung.
... und wer Andre Weils Buch " Basic Number Theory" wirklich durchgearbeitet hat, wird wissen, was ich meine (denn was er als einen schon hinreichend kleinen, überzeugenden Gedankensprung da so alles stehen lässt, kann schon mal ein bis zwei Stunden Arbeit kosten, es einzusehen. Einen Fehler aber konnten wir, die wir sein Buch damals im Detail durchgearbeitet haben, ihm aber wirklich NIEMALS nachweisen. Wie gesagt: Ich bewundere ihn ...
Irena aus 1107-20:Zitat:Der allseits geachtete Physiker Steven Hawking scheint zu denken, jedes mathematische Modell sei auch ein physikalisches.
Passt auf wie dein Satz ändert, wenn du statt Begriff "ist" (was einer Äquivalenz zeigt) den Begriff "entspricht" nutzt. "Jedes mathematische Modell entspricht einem physikalischen". Andere Begriff zeigt auf den Bezug, nicht Äquivalenz.
Wobei auch hier ein Denkfehler, weil es ein Gegenteil richtig ist: jedes physikalischen Model entspricht dem mathematischen, da wir wissen, es gibt mathematische Modelle, die die Naturwissenschaft Physik "sprengen". Die Anwendung in Quantenmechanik verschiedener mathematische Modelle zeigt nur innere Beziehung der mathematischen Modelle.
Dein erstes Argument scheint mir einfach nur ein Spiel mit Worten — es sagt rein gar nichts.
Zum zweiten: Wer etwas modelliert (mit oder ohne Mathematik) wird i.A. zu einem Modell kommen, welches irgendwo hinkt, und somit den zu modellierenden Gegenstand eben NICHT mehr in allen Einzelheiten korrekt abbildet. Das sehe ich als Selbstverständlichkeit — es ist sogar zwangsläufig so, denn ein Modell soll ja häufig auch vereinfachen (sich also auf nur bestimmte Aspekte konzentrieren).
Irena aus 1107-20:Zuletzt ein Beispiel, der mich auf Palme bringt, wenn es lese (bei deinen Ausführungen leider zu viel ähnliches Textes). Nehmen wir den folgenden Absatz zur Analyse:
Zitat:Ein Vergleich der Ergebnisse von Kurt Gödel einerseits und Gerhard Gentzen sowie Paul Lorenzen andererseits zeigt meiner Ansicht nach deutlich, dass konstruktive und nicht konstruktive Modelle grundsätzlich verschiedener Natur sind. Der Unterschied besteht darin, dass viele Ergebnisse indirekter Beweisführung schon ihrer Natur nach nicht Ergebnis rein konstruktiver Mathematik sein können. Es bleibt offen, ob man auch sie als mathematische Wahrheiten sehen kann, die mehr sind als nur eine gedankliche Konstruktion.
Zitat:...konstruktive und nicht konstruktive Modelle grundsätzlich verschiedener Natur sind.
Okay, nehmen wir es an. Es ist mir hier die Richtigkeit der Annahme von sekundäre Bedeutung ist.
Bitte liest dein Satz aufmerksam. Wie sprechen über grundsätzliche Unterschiede, oder? Wenn man spricht über "viele", bedeutet es nicht an "alle" anwendbar und daher nicht grundsätzlich sein kann.Zitat:Der Unterschied besteht darin, dass viele Ergebnisse indirekter Beweisführung schon ihrer Natur nach nicht Ergebnis rein konstruktiver Mathematik sein können.
Auch was du hier sagst, scheint mir nur ein Spiel mit Worten.
Dass mein Statement "... viele Ergebnisse indirekter Beweisführung schon ihrer Natur nach nicht Ergebnis rein konstruktiver Mathematik sein können" durchaus richtig ist, zeigt sich sehr schön in Beitrag 1107-22, wo wir im zweiten Kullerpunkt ja tatsächlich einen indirekten Beweis führen. Über rein konstruktive Mathematik wäre ganz sicher NICHT beweisbar, dass K lügt.
Irena aus 1107-20:Nächste Vorwand. Mit dem Satz solltest du den ersten Satz erklären bzw. erweitern. Du machst aber Zirkelsprung und erklärst die Annahme durch sie selbst.
Ich habe keine Anhnung, wo da ein Zirkelschluss sein sollte.
Irena aus 1107-20:Übrigens der Tisch ist nicht gleich Stuhl, gehören beide aber zu Möbel. "Die Natur" von beiden sicher verschieden ist: auf einem sitzen wir, auf anderen essen. Dennoch durch eine übergeordnete Klasse "das Möbel" zeigen sie ihre gemeinsame "Natur". Ähnlich ist mit der direkten und indirekten Beweisführung.
Da bin ich völlig deiner Meinung:
- Beide Beweiswege sind mathematisch exakte Beweiswege (so wie Stuhl und Tisch beides Möbel sind),
- sind aber dennoch verschieden (so wie auch Stuhl und Tisch verschieden sind).
Irena aus 1107-20:Zitat:Es bleibt offen, ob man auch sie als mathematische Wahrheiten sehen kann, die mehr sind als nur eine gedankliche Konstruktion.
"Sie" muss wohl indirekte Beweisführung sein. Ist direkte Beweisführung etwas anders als gedankliche Konstruktion?! Da musst du wohl erklären, da für mich es offensichtlich ist. Wenn ich auch semantischen Inhalt dieses Satzes ein Augenblick nicht beachte, dann trotzdem ist mir nicht klar, warum aus den vorhergehenden Kontext muss etwas "offen bleiben". Aus der vorigen Sätze folgt keinesfalls die Offenheit des Problems.
Nachdem man indirekt bewiesene Wahrheiten nicht konstruieren kann, könnte man sich schon fragen, ob sie wirklich einen realen Teil der Natur darstellen.
Problem nur: Wie will man den Begriff real den nun wirklich genau definieren?
Irena aus 1107-20:u. s. w.
Schade, dass dir hier offenbar die Puste aus geht ...
Gruß, grtgrt
Beitrag 1107-44
Was genau ist denn nun eigentlich Realität (reale Wirklichkeit)?
Irena:
Was ich in Beitrag 1896-9 schrieb, scheint mir Beweis genug, dass ich auch der Philosophie genügend Beachtung schenke — was mich aber keineswegs daran hindert, den mehr pragmatischen Standpunkt der Physiker mehr zu schätzen (z.B. deswegen, weil ich keineswegs sicher bin, dass moderne Philosophen immer so ganz genau wissen, wovon sie denn eigentlich reden):
Gruß, grtgrt
Irena aus 1107-28:Zitat von grtgrt:Nachdem man indirekt bewiesene Wahrheiten nicht konstruieren kann, könnte man sich schon fragen, ob sie wirklich einen realen Teil der Natur darstellen.
Problem nur: Wie will man den Begriff real den nun wirklich genau definieren?
O man, ich sehe viel mehr Begriffe, die genau definiert müssen. Vielleich müsstest du mehr Aufmerksamkeit der Philosophie schenken als Matheamtik.
Irena:
Was ich in Beitrag 1896-9 schrieb, scheint mir Beweis genug, dass ich auch der Philosophie genügend Beachtung schenke — was mich aber keineswegs daran hindert, den mehr pragmatischen Standpunkt der Physiker mehr zu schätzen (z.B. deswegen, weil ich keineswegs sicher bin, dass moderne Philosophen immer so ganz genau wissen, wovon sie denn eigentlich reden):
Grtgrt aus 1896-9:
Auf jeden Fall muss man zur Kenntnis nehmen, dass die Anfang des 20. Jahrhunderts entwickelte Quantentheorie eine philosophische Revolution zur Folge hatte, deren zentrale Erkenntnisse waren:
Die Natur funktioniert keineswegs voll deterministisch.
und auch alle sonstige Realität, existiert stets nur ungenau.
Einstein war der letzte große Physiker, der das nicht glauben konnte.
John Wheeler hat den Unterschied der alten und der neuen Weltsicht auf den Punkt gebracht über ein erfundenes Gesprächs zwischen Baseball Schiedsrichtern:Ironischerweise ergänzt die Relativitästheorie:
- Erster (Einstein): Ich entscheide, wie es ist.
- Zweiter (Bohr): Ich entscheide, wie ich es sehe.
- Dritter (Messung): Solange ich nichts entscheide, war auch nichts.
... und keine zwei Schiedsrichter sehen dasselbe.
Der Physiker Roger G. Newton sagt deswegen auch folgerichtig (1993):
Physiker kümmern sich nicht um so metaphysische Begriffe wie Existenz; sie versuchen nicht, die letzte Realität zu ergründen, was auch immer man darunter verstehen mag. Die Bausteine für unsere grundlegenden Vorstellungen über die Welt werden danach ausgewählt, ob sie ein kohärentes Gedankengebäude ermöglichen.
Gruß, grtgrt
Beitrag 1701-20
Zum Begriff physikalischer Objekte: seine wohl beste Definition
An alle:
Dieser Versuch, den Begriff physikalisches Objekt zu definieren, scheint mir der bisher beste.
Danke, grtgrt
Zur Info: Ein Teil dieser Diskussion wurde an anderer Stelle geführt und ist dort beendet worden mit Beitrag 1896-19 und Beitrag 1896-20.
H... aus 1701-19:phys. Objekt: ganz simple ein Sachverhalt, der einer physikalischen Betrachtung unterzogen werden kann. Der Sachverhalt kann wahrnehmbarer oder rein theoretischer Natur sein (z.B. war das Higgs Boson viele Jahre ein rein theor. phys. Objekt,
seit einigen Wochen besteht Hoffnung, dass nun das Standardmodell komplett ist).
phys. Größe: eine Eigenschaft des Sachverhalts (=phys. Objekt)
Gruß H... R.
An alle:
Dieser Versuch, den Begriff physikalisches Objekt zu definieren, scheint mir der bisher beste.
Danke, grtgrt
Zur Info: Ein Teil dieser Diskussion wurde an anderer Stelle geführt und ist dort beendet worden mit Beitrag 1896-19 und Beitrag 1896-20.
Beitrag 1896-1
Was Niels Bohr uns sagt
Niels Bohr — Nobelpreisträger und Mitbegründer der Quantenphysik — soll einmal gesagt haben:
Auch Richard Feynman war der Meinung:
Damit scheint klar: Physik besteht aus zwei Teilen
dem
Beobachten der Natur (Experimentalphysik)
und dem Modellieren der Natur (Theoretische Physik).
Man sollte aber niemals glauben, so ein Modell sei die Natur.
Warum aber modelliert man die Natur ausschließlich über Mathematik? Und warum scheint die dafür so geeignet? Hier die Antwort darauf:
Mathematik besteht aus zweierlei: Einer Denkmethodik und der Menge aller mathematischen Gesetze.
Was wir als mathematische Methodik haben ist lediglich der beste Weg, den der Mensch bisher fand, über mathematische Gesetze nachzudenken (dieser Weg könnte austauschbar sein und wird, sobald Quantencomputer verfügbar sind, fast sicher eine Art Bruder bekommen).
Ganz anders mathematische Gesetze: Sie existieren ganz unabhängig davon, ob der Mensch sie kennt oder nicht — der Mensch kann sie entdecken, aber z.B. nicht abändern.
Damit ist klar:
Mathematische Gesetze sind Teil der Natur
und Mathematik kann als der Teil der Physik verstanden werden, der diesen Teil der Natur entdeckt
und diskutierbar macht (modelliert).
Insbesondere gilt: Die Stringtheorie ist eine rein mathematische Theorie, und so ist jeder Zusammenhang, den sie entdeckt, ein mathematisches Gesetz und damit wirklich Teil der Natur — ein Puzzlestein also, von dem aber recht lange unklar sein kann, in welches unserer (Teil-) Modelle der Natur er denn am besten passt.
Da Stringtheorie eine Art Gleichungssystem ist, das — so schätzt man — etwa 10500 Lösungen hat, deren jede Modell eines möglichen Universums ist, wird klar, wie viele Puzzlesteine es mindestens gibt und wie wenig davon wir bisher schon kennen (!).
Niels Bohr — Nobelpreisträger und Mitbegründer der Quantenphysik — soll einmal gesagt haben:
Zitat:Die Physik kann nicht ergründen, wie die Natur funktioniert.
Aufgabe der Physik ist lediglich, zu untersuchen, wie die Natur sich uns zeigt.
Auch Richard Feynman war der Meinung:
Zitat:I can savely say: Nobody understands Quantum Physics.
Damit scheint klar: Physik besteht aus zwei Teilen
und dem Modellieren der Natur (Theoretische Physik).
Man sollte aber niemals glauben, so ein Modell sei die Natur.
Warum aber modelliert man die Natur ausschließlich über Mathematik? Und warum scheint die dafür so geeignet? Hier die Antwort darauf:
Mathematik besteht aus zweierlei: Einer Denkmethodik und der Menge aller mathematischen Gesetze.
Was wir als mathematische Methodik haben ist lediglich der beste Weg, den der Mensch bisher fand, über mathematische Gesetze nachzudenken (dieser Weg könnte austauschbar sein und wird, sobald Quantencomputer verfügbar sind, fast sicher eine Art Bruder bekommen).
Ganz anders mathematische Gesetze: Sie existieren ganz unabhängig davon, ob der Mensch sie kennt oder nicht — der Mensch kann sie entdecken, aber z.B. nicht abändern.
Damit ist klar:
und Mathematik kann als der Teil der Physik verstanden werden, der diesen Teil der Natur entdeckt
und diskutierbar macht (modelliert).
Insbesondere gilt: Die Stringtheorie ist eine rein mathematische Theorie, und so ist jeder Zusammenhang, den sie entdeckt, ein mathematisches Gesetz und damit wirklich Teil der Natur — ein Puzzlestein also, von dem aber recht lange unklar sein kann, in welches unserer (Teil-) Modelle der Natur er denn am besten passt.
Da Stringtheorie eine Art Gleichungssystem ist, das — so schätzt man — etwa 10500 Lösungen hat, deren jede Modell eines möglichen Universums ist, wird klar, wie viele Puzzlesteine es mindestens gibt und wie wenig davon wir bisher schon kennen (!).
Beitrag 1896-3
Was ist real?
Hallo Herr Bauhof,
Sie sehen das eindeutig zu eng, denn ganz grundsätzlich gilt:
Es gibt
beobachtete, vermutete, und extrapolierte physikalische Ergebnisse:
Hier zwei Beispiele extraplolierter Physik:
Siehe auch: Zu extrapolierender (und auch extrapolierter) Physik.
Mit besten Grüßen,
Gebhard Greiter (= grtgrt)
Hallo Herr Bauhof,
Sie sehen das eindeutig zu eng, denn ganz grundsätzlich gilt:
Es gibt
- Beobachtete sind die durch Experimente bestätigten (das was uns Experimentalphysik und Astronomie liefern).
- Vermutete Ergebnisse sind solche, die als Idee schon entstanden, in der Welt um uns herum aber noch nicht beobachtet werden konnten.
- Extrapolierte sind jene vermuteten, die uns durch rein mathematische Überlegungen nahegelegt werden.
Hier zwei Beispiele extraplolierter Physik:
- Quantenverschränkung ist ein physikalisches Phänomen, welches zunächst rein nur auf mathematischem Wege entdeckt wurde. Die entsprechende Herleitung stammt von Einstein, Podolosky und Rosen und wurde — mindestens durch Einstein — als eine Widerlegung der Korrektheit des mathematischen Modells der Quantenmechanik angesehen: Dass eine derart "spukhafte Fernwirkung" wirklich existieren könnte, haben Einstein, Podolsky und Rosen einfach nicht glauben wollen. Erst gut 40 Jahre später hat Experimentalphysik sie nachweisen können — und das auch nur deswegen, weil (etwa 1960) John Bell die sog. Bellsche Ungleichung entdeckt hatte (ihr Gegenstand sind gewisse Wahrscheinlichkeiten). Man erkennt an diesem Beispiel, wie lange es dauern kann, bis aus extrapolierter Physik tatsächlich beobachtete wird.
- Supersymmetrie ist ein zweites wichtiges Beispiel extrapolierter Physik. Experimentalphysik konnte in der Welt um uns herum noch keinen Beweis dafür finden. Sie ist bislang einfach nur eine Entdeckung der Stringtheorie, dort aber wichtig, denn nur jene Modelle der Stringtheorie, die supersymmetrisch sind, reproduzieren alle aus dem Standardmodell der Elementarteilchenphysik bekannten Partikel. Da supersymmetrische Transformation eines supersymmetrischen Weltmodells Bosonen und Fermionen miteinander vertauscht ohne die physikalischen Aussagen des Modells zu verändern, würde — das grundsätzlich verschiedene Verhalten von Bosonen und Fermionen berücksichtigt — ohne Mathematik niemand auf die Idee kommen, unsere Welt könne supersymmetrisch sein. Dennoch haben schon 1970 zwei Gruppen von Forschern — unabhängig voneinander, und nur mit Hilfe mathematischer Überlegungen — bewiesen, dass das Standardmodell verträglich wäre mit einer Vertauschung der Rollen, die darin Bosonen und Fermionen spielen. Damit gibt es mindestens zwei grundverschiedene mathematische Argumente, die darauf hindeuten, unsere Welt könne supersymmetrische sein.
Siehe auch: Zu extrapolierender (und auch extrapolierter) Physik.
Mit besten Grüßen,
Gebhard Greiter (= grtgrt)
Beitrag 1896-4
Naturgesetze
Hallo Eugen,
Als menschliche Geisteswissenschaft kann ich beim besten Willen nur mathematische Methodik sehen — niemals aber mathematische Gesetzmäßigkeiten; die nämlich haben mit absoluter Sicherheit schon immer gegolten — lange bevor es Menschen, die Erde, oder gar unser Sonnensystem gab.
Hier drei Beispiele:
Mit besten Grüßen,
grtgrt (= Gebhard Greiter)
PS: Hier noch ein Beispiel für ein mathematisches Naturgesetz, das wir noch nicht kennen, dessen Auswirkung wir aber beobachten:
Bauhof aus 1896-2:Grtgrt aus 1896-1:
Ganz anders mathematische Gesetze: Sie existieren ganz unabhängig davon, ob der Mensch sie kennt oder nicht — der Mensch kann sie entdecken, aber
z.B. nicht abändern.
Das ist die Auffassung der ’Platoniker’ unter den Mathematikern. Aber auch das sehe ich anders. Die Mathematik gilt als menschliche Geisteswissenschaft und nicht als Naturwissenschaft. Ohne die Existenz von Menschen existiert auch keine Mathematik.
M.f.G. Eugen Bauhof
Hallo Eugen,
Als menschliche Geisteswissenschaft kann ich beim besten Willen nur mathematische Methodik sehen — niemals aber mathematische Gesetzmäßigkeiten; die nämlich haben mit absoluter Sicherheit schon immer gegolten — lange bevor es Menschen, die Erde, oder gar unser Sonnensystem gab.
Hier drei Beispiele:
- Es gibt sicher keinen Sinn anzunehmen, dass z.B. das mathematische Gesetz, welches von Pythagoras entdeckt wurde (und etwas über einen Zusammenhang zwischen den Längen der Seiten rechtwinkliger Dreiecke aussagt), nicht schon vor ihm richtig war.
- Ein noch überzeugenderes Beispiel: Sämtliche mathematischen Gesetze, die gleichseitige 5-Ecke betreffen (und wie man sie zur Oberfläche eines fußballartigen Körpers anordnen kann), sind durch die Natur selbst schon lange vor dem Menschen genutzt worden: so etwa beim Bau der Fullerene (das sind hoch sysmmetrische Moleküle bestehend aus je 60 Kohlenstoffatomen).
- Auch jeder in der Natur vorkommende Kristall hat eine Struktur, die den Gesetzmäßigkeiten 3-dimensionaler Geometrie gehorcht. Wir sehen: Kristalle und komplexe Moleküle sind eine Art Buch, in dem die Natur selbst mathematische Gesetze formuliert und demonstriert (!).
Mit besten Grüßen,
grtgrt (= Gebhard Greiter)
PS: Hier noch ein Beispiel für ein mathematisches Naturgesetz, das wir noch nicht kennen, dessen Auswirkung wir aber beobachten:
Zitat von Igor und Grichta Bogdanov (Inhaber des Lehrstuhls für Kosmologie an der Uni Belgrad):Wenn Sie im Sommer an einer Wiese vorbeigehen, pflücken Sie doch mal wahllos ein paar Margeriten, und zählen Sie ihre Blütenblätter. ... Sie werden keine finden, die 7 hat, oder 16. Wieso? Weil auch die Zahl der Blütenblätter einer Blume kein Zufall ist. Tatsächlich folgt sie einem mathematischen Gesetz, das in den Tiefen der Blüte verborgen wirkt.
Und wieder ist die Frage: Woher kommt dieses Gesetz?
Beitrag 1896-5
Natur und Modell
Aus was besteht eigentlich der Beobachter?�
Grtgrt aus 1896-1:Physik besteht aus zwei Teilen
dem Beobachten der Natur (Experimentalphysik)
und dem Modellieren der Natur (Theoretische Physik).
Man sollte aber niemals glauben, so ein Modell sei die Natur.
Aus was besteht eigentlich der Beobachter?�
Beitrag 1896-8
absolutes Axiom
Hi Henry,
kann Dich verstehen; auch ich selbst dachte lange Zeit, die Mathematik sei nur ein gedankliches Gebäude. Warum aber lassen sich dann selbst so völlig unvermutete Eigenschaften der Natur (wie etwa Quantenverschränkung) mit ihrer Hilfe entdecken?
Erst seitdem mir klar wurde, dass mathematische Gesetze auch dann gelten, wenn wir sie nicht kennen, und dass sie von ganz anderer Qualität sind als mathematische Methodik, bin ich der Überzeugung, sie seien Naturgesetze.
Methodik ist austauschbar — Naturgesetze sind es nicht.
ABER: Naturgesetze sind Aussagen, die unter jeder Voraussetzung wahr sind.
Wenn ich also sage, jedes mathematische Gesetz sei ein Naturgesetz, dann meine ich damit natürlich eine Formulierung dieses Gesetzes, die alle notwendigen Voraussetzungen explizit nennt. (So weit also zu Deinen Beispielen).
Mehr zu diesem Thema findet sich auf meiner Seite Welcher Teil der Mathematik ist absolutes Axiom?.
Beste Grüße,
grtgrt = Gebhard Greiter
Henry aus 1896-6:Zitat von Gebhard:Kurz: Man muss nicht Platoniker sein, um zu sehen, dass mathematische Gesetze Naturgesetze sind.
Mit besten Grüßen,
Hallo, Gebhard!
Ich denke nicht, dass die Mathematik grundlegend ist. Das System "Mathematik" beruht auf Lehrsätzen, die wiederum von Axiomen abhängen. Nimm z. B. Pi, die Kreiszahl. Sie beruht auf dem Verhältnis von Radius und Umfang. Aber nur in der Euklidischen Ebene! Lokal beschreibt Pi selbstverständlich das Verhältnis korrekt. Aber ist unser Kosmos denn mit der Euklidischen Geometrie zu beschreiben? Und wenn nicht, mit welcher Geometrie dann? Riemann? Minkowski? Ist er denn überhaupt lokal? Welche Geometrie beschreibt den Kosmos bzw. genauer gesagt die Raumzeit?
Hi Henry,
kann Dich verstehen; auch ich selbst dachte lange Zeit, die Mathematik sei nur ein gedankliches Gebäude. Warum aber lassen sich dann selbst so völlig unvermutete Eigenschaften der Natur (wie etwa Quantenverschränkung) mit ihrer Hilfe entdecken?
Erst seitdem mir klar wurde, dass mathematische Gesetze auch dann gelten, wenn wir sie nicht kennen, und dass sie von ganz anderer Qualität sind als mathematische Methodik, bin ich der Überzeugung, sie seien Naturgesetze.
Methodik ist austauschbar — Naturgesetze sind es nicht.
ABER: Naturgesetze sind Aussagen, die unter jeder Voraussetzung wahr sind.
Wenn ich also sage, jedes mathematische Gesetz sei ein Naturgesetz, dann meine ich damit natürlich eine Formulierung dieses Gesetzes, die alle notwendigen Voraussetzungen explizit nennt. (So weit also zu Deinen Beispielen).
Mehr zu diesem Thema findet sich auf meiner Seite Welcher Teil der Mathematik ist absolutes Axiom?.
Beste Grüße,
grtgrt = Gebhard Greiter
Beitrag 1896-9
Zum Wesen physikalischer Aussagen — ein Schiedsrichter irrt
Hi Henry,
Niels Bohr soll mal gesagt haben:
Die Physik kann nicht ergründen, wie die Natur beschaffen ist.
Aufgabe der Physik ist nur, darüber zu diskutieren, wie die Natur sich uns zeigt.
Kein Wunder also, dass du kein Modell kennst, das uns sagt, was dieses oder jenes physikalische Objekt (als Teil der Natur gemeint) denn nun wirklich ist.
Alles was wir haben, sind Modelle, mit denen wir versuchen, die Natur nachzubilden mit dem Ziel, vorhersagbar zu machen, welches Verhalten sie in dieser oder jener Situation zeigen wird.
Noch genauer: Unsere Modelle sind Mechanismen, das Verhalten der Natur nachzubilden — keineswegs aber was sie wirklich ist (und so ist es kein Wunder, dass Stringtheoretiker zunehmend mehr völlig unterschiedliche Modelle finden, die identisches physikalisches Verhalten bedeuten).
Siehe auch: Zum Wesen physikalischer Aussagen.
Beste Grüße,
grtgrt = Gebhard Greiter
PS: Heisenberg übringens sah das wie Bohr, als er schrieb:
Auf jeden Fall muss man zur Kenntnis nehmen, dass die Anfang des 20. Jahrhunderts entwickelte Quantentheorie eine philosophische Revolution zur Folge hatte, deren zentrale Erkenntnisse waren:
Die Natur funktioniert keineswegs voll deterministisch.
und auch alle sonstige Realität, existiert stets nur ungenau.
Einstein war der letzte große Physiker, der das nicht glauben konnte.
John Wheeler hat den Unterschied der alten und der neuen Weltsicht auf den Punkt gebracht über ein erfundenes Gesprächs zwischen Baseball Schiedsrichtern:
... und keine zwei Schiedsrichter sehen dasselbe.
Der Physiker Roger G. Newton sagt deswegen auch folgerichtig (1993):
Physiker kümmern sich nicht um so metaphysische Begriffe wie Existenz; sie versuchen nicht, die letzte Realität zu ergründen, was auch immer man darunter verstehen mag. Die Bausteine für unsere grundlegenden Vorstellungen über die Welt werden danach ausgewählt, ob sie ein kohärentes Gedankengebäude ermöglichen.
Henry aus 1896-6:Und was beschreiben die mathematischen Modelle der Physik? Das Verhalten von physikalischen Objekten, die Stärke der Kräfte, ihre Beziehungen zueinander. Ich kenne kein Modell, dass uns sagt, was physikalische Objekte SIND. Gibt es ein mathematisches Modell, das das leistet? Was IST ein Elektron? Was IST eine elektrische Ladung?
Hi Henry,
Niels Bohr soll mal gesagt haben:
Aufgabe der Physik ist nur, darüber zu diskutieren, wie die Natur sich uns zeigt.
Kein Wunder also, dass du kein Modell kennst, das uns sagt, was dieses oder jenes physikalische Objekt (als Teil der Natur gemeint) denn nun wirklich ist.
Alles was wir haben, sind Modelle, mit denen wir versuchen, die Natur nachzubilden mit dem Ziel, vorhersagbar zu machen, welches Verhalten sie in dieser oder jener Situation zeigen wird.
Noch genauer: Unsere Modelle sind Mechanismen, das Verhalten der Natur nachzubilden — keineswegs aber was sie wirklich ist (und so ist es kein Wunder, dass Stringtheoretiker zunehmend mehr völlig unterschiedliche Modelle finden, die identisches physikalisches Verhalten bedeuten).
Siehe auch: Zum Wesen physikalischer Aussagen.
Beste Grüße,
grtgrt = Gebhard Greiter
PS: Heisenberg übringens sah das wie Bohr, als er schrieb:
Quelle: Werner Heisenberg: Physik und Philosophie. Stuttgart: Hirzel, 1959Zitat von Heisenberg:Bei Experimenten über atomares Geschehen haben wir es mit Dingen und Tatsachen zu tun, die ebenso real sind wie irgendein Phänomen im täglichen Leben. Aber die Atome und Elementarteilchen sind nicht gleichermaßen real; sie bilden eher eine Welt von Möglichkeiten als eine von Dingen oder Tatsachen.
Auf jeden Fall muss man zur Kenntnis nehmen, dass die Anfang des 20. Jahrhunderts entwickelte Quantentheorie eine philosophische Revolution zur Folge hatte, deren zentrale Erkenntnisse waren:
und auch alle sonstige Realität, existiert stets nur ungenau.
Einstein war der letzte große Physiker, der das nicht glauben konnte.
John Wheeler hat den Unterschied der alten und der neuen Weltsicht auf den Punkt gebracht über ein erfundenes Gesprächs zwischen Baseball Schiedsrichtern:
- Erster (Einstein): Ich entscheide, wie es ist.
- Zweiter (Bohr): Ich entscheide, wie ich es sehe.
- Dritter (Messung): Solange ich nichts entscheide, war auch nichts.
Der Physiker Roger G. Newton sagt deswegen auch folgerichtig (1993):
Physiker kümmern sich nicht um so metaphysische Begriffe wie Existenz; sie versuchen nicht, die letzte Realität zu ergründen, was auch immer man darunter verstehen mag. Die Bausteine für unsere grundlegenden Vorstellungen über die Welt werden danach ausgewählt, ob sie ein kohärentes Gedankengebäude ermöglichen.
Beitrag 1896-11
Ein physikalisches Objekt — was genau ist das?
Hi Harti,
meine Aussage auf Seite Zum Wesen physikalischer Aussagen
darf natürlich nicht so verstanden werden, dass umgekehrt auch jedes gedankliche Modell ein physikalisches Objekt sei.
Gruß, grtgrt
Hi Harti,
meine Aussage auf Seite Zum Wesen physikalischer Aussagen
Zitat von grtgrt:Physikalische Objekte sind nichts anderes als gedankliche Modelle,
die der Mensch sich macht, aus dem Wunsch heraus,
das Verhalten der Natur verstehbar und vorhersagbar zu machen.
darf natürlich nicht so verstanden werden, dass umgekehrt auch jedes gedankliche Modell ein physikalisches Objekt sei.
Gruß, grtgrt
Beitrag 1896-14
Realität, Abstrakion, oder ...
Nein Harti,
wir sind uns da NICHT einig, denn:
Niels Bohr und Werner Heisenberg (siehe Beitrag 1896-9) sagen ganz klar, dass man die Natur nicht verwechseln darf mit dem Bild, das wir uns von ihr machen. Heisenberg sagt explizit, dass z.B. Atome oder Elementarteilchen mehr eine Welt von Möglichkeiten sind als eine von Dingen oder Tatsachen.
Atome, Elementarteilchen, und auch jedes andere sog. physikalische Objekt sind Subobjekte unseres Verständnisses von der Natur (des Modells also, das wir uns von der Natur machen) — sind aber nicht notwendig genau so auch Teil der Natur selbst.
Die Umgangssprache, Du und fast jeder Mensch sonst auch ignoriert diesen Unterschied.
Das ist meist tragbar, aber sicher nicht dort, wo man — wie hier in diesem Blog — den Dingen und ihrem Wesen wirklich auf den Grund gehen möchte.
Allein schon die Tatsache, dass sich die Definition wenig gut verstandener physikalischer Objekte ändert, sobald man sie besser versteht, zeigt, dass Bohr und Heisenberg recht haben.
Mfg, grtgrt
Harti aus 1896-12:Hallo Grtgrt,
dann sind wir uns ja wohl einig, dass eine Gleichsetzung von gedanklichem Modell (Vorstellung) und physikalischem Objekt (Wirklichkeit) unzweckmäßig ist.
MfG
Harti
Nein Harti,
wir sind uns da NICHT einig, denn:
Niels Bohr und Werner Heisenberg (siehe Beitrag 1896-9) sagen ganz klar, dass man die Natur nicht verwechseln darf mit dem Bild, das wir uns von ihr machen. Heisenberg sagt explizit, dass z.B. Atome oder Elementarteilchen mehr eine Welt von Möglichkeiten sind als eine von Dingen oder Tatsachen.
Atome, Elementarteilchen, und auch jedes andere sog. physikalische Objekt sind Subobjekte unseres Verständnisses von der Natur (des Modells also, das wir uns von der Natur machen) — sind aber nicht notwendig genau so auch Teil der Natur selbst.
Die Umgangssprache, Du und fast jeder Mensch sonst auch ignoriert diesen Unterschied.
Das ist meist tragbar, aber sicher nicht dort, wo man — wie hier in diesem Blog — den Dingen und ihrem Wesen wirklich auf den Grund gehen möchte.
Allein schon die Tatsache, dass sich die Definition wenig gut verstandener physikalischer Objekte ändert, sobald man sie besser versteht, zeigt, dass Bohr und Heisenberg recht haben.
Mfg, grtgrt
Beitrag 1896-15
Wirklichkeit
Hi Henry,
genau das Gegenteil ist der Fall:
Nach Bohr und Heisenberg kann die Realität sehr wohl außerhalb unseres Bewusstsein liegen. Beide betrachten das eher als den Normalfall.
Bitte beachte: Was uns bewusst ist, machen wir zu einem Teil unseres Modells der Wirklichkeit.
Gruß, grtgrt
Henry aus 1896-13:... es bleibt das gravierende Problem, dass - FALLS - physikalische Objekte nur gedankliche Modelle sind, es keine Wirklichkeit außerhalb eines Bewusstseins gibt.
Hi Henry,
genau das Gegenteil ist der Fall:
Nach Bohr und Heisenberg kann die Realität sehr wohl außerhalb unseres Bewusstsein liegen. Beide betrachten das eher als den Normalfall.
Bitte beachte: Was uns bewusst ist, machen wir zu einem Teil unseres Modells der Wirklichkeit.
Gruß, grtgrt
Beitrag 2039-63
Zum Unterschied von Wirklichkeit und Realität
Zum Unterschied von Wirklichkeit und Realität
In Dürr & Österreicher: Wir erleben mehr als wir begreifen liest man:
2 Wird von mir als Summe aller Kraftpotentiale verstanden
In Dürr & Österreicher: Wir erleben mehr als wir begreifen liest man:
Zitat von Dürr, S. 37 und 39:
Wirklichkeit ist im Grunde Potentialität, nicht Realität.
Das eine, unauftrennbare, potentielle Wellengebirge2, einem Weltmeer gleich, kann sich aber so überlagern, dass das Gewoge sich nur an wenigen Stellen addiert, sich konstruktiv überlagert und sich im Übrigen, durch destruktive Interferenz, zu Null, einer glatten See, herausmittelt.
So entsteht am Ende die Realität als Ergebnis eines grandiosen ausmittelnden Überlagerungseffektes.
... das, was sozusagen überlebt bei all diesen Überlagerungsprozessen, das ist das, was wir sehen, was wir hinterher als Realität1 anfassen.
1 Realität von lat. res = das Ding, die Sache
2 Wird von mir als Summe aller Kraftpotentiale verstanden
Beitrag 1896-17
Physik kann nicht entscheiden ...
Hi Henry,
es ist mir absolut unverständlich, warum mein Argument bedeuten sollte, dass wir die Wirklichkeit schaffen.
Wir schaffen Modelle, sprich: physikalische Objekte — Theorien also, die zeigen, wie wir uns die Natur vorstellen. Ob sie wirklich so beschaffen ist, steht auf einem ganz anderem Blatt und kann — so sagt Niels Bohr — durch die Physik nicht entschieden werden.
Du scheinst physikalische Objekte als Teil der Natur zu sehen, Bohr tut das nicht, und so findet die moderne Theoretische Physik es auch gar nicht mehr so verwunderlich, dass es für ein und denselben Teil der Natur deutlich unterschiedliche Modelle geben kann, die beide gleiches Naturgesetz zum Ausdruck bringen (also gleich richtig sein können).
Gruß, grtgrt
es ist mir absolut unverständlich, warum mein Argument bedeuten sollte, dass wir die Wirklichkeit schaffen.
Wir schaffen Modelle, sprich: physikalische Objekte — Theorien also, die zeigen, wie wir uns die Natur vorstellen. Ob sie wirklich so beschaffen ist, steht auf einem ganz anderem Blatt und kann — so sagt Niels Bohr — durch die Physik nicht entschieden werden.
Du scheinst physikalische Objekte als Teil der Natur zu sehen, Bohr tut das nicht, und so findet die moderne Theoretische Physik es auch gar nicht mehr so verwunderlich, dass es für ein und denselben Teil der Natur deutlich unterschiedliche Modelle geben kann, die beide gleiches Naturgesetz zum Ausdruck bringen (also gleich richtig sein können).
Gruß, grtgrt
Beitrag 1896-20
Ein missverständlicher Begriff: physikalisches Objekt
Hallo, Gebhard,
wir kommen der Sache langsam näher! Ich kann nur für mich sprechen: Mit einem "physikalischen Objekt" meine ich einen quantifizierbaren, also messbaren Teil der Natur und nicht das Modell davon. (Dass sich die Physik nun mit den messbaren Eigenschaften ihrer Objekte befasst, ist natürlich nicht meine Idee.)
Die "physikalischen Objekte " sind auch Teil der Natur, aber nicht einfach "Synonym für Teil der Natur". Ein Mensch (ein Lebewesen) ist ein physikalisches Objekt, aber wer will behaupten, es würde mit einer physikalischen Beschreibung vollständig erfasst sein? Objekte der Natur sind mehr als quantifizierbare Einheiten, sie "sind" auch und vor allen Dingen Qualität, und die lässt sich nicht messen. Ein Elektron z. B. ist ein physikalisches Objekt, über das wir nur in Modellen aufgrund von Messungen etwas aussagen können. Wenn wir auch nicht sagen können, was ein Elektron letztlich tatsächlich ist (wir also nichts über seine Qualität sagen können), so ist es aber dieses "Etwas", über das unsere Modelle Aussagen machen.
Henry�
Grtgrt aus 1896-19:
Henry und Harti,
die Tatsache, dass ihr — anders als ich — den Begriff "physikalisches Objekt" als Synonym für "ein Teil der Natur" seht, zeigt mir, dass ich in Zukunft wohl besser von physikalischen Modellen (statt Objekten) sprechen sollte.
Ein Elektron, aber z.B. auch ein ganzes Universum, wären dann also stets zu verstehen als ein Teil der Natur, dessen Verhalten wir zu beschreiben suchen über ein oder mehrere — gleichwertige oder einander ergänzende — Modelle.
Danke & Gruß,
grtgrt
Hallo, Gebhard,
wir kommen der Sache langsam näher! Ich kann nur für mich sprechen: Mit einem "physikalischen Objekt" meine ich einen quantifizierbaren, also messbaren Teil der Natur und nicht das Modell davon. (Dass sich die Physik nun mit den messbaren Eigenschaften ihrer Objekte befasst, ist natürlich nicht meine Idee.)
Die "physikalischen Objekte " sind auch Teil der Natur, aber nicht einfach "Synonym für Teil der Natur". Ein Mensch (ein Lebewesen) ist ein physikalisches Objekt, aber wer will behaupten, es würde mit einer physikalischen Beschreibung vollständig erfasst sein? Objekte der Natur sind mehr als quantifizierbare Einheiten, sie "sind" auch und vor allen Dingen Qualität, und die lässt sich nicht messen. Ein Elektron z. B. ist ein physikalisches Objekt, über das wir nur in Modellen aufgrund von Messungen etwas aussagen können. Wenn wir auch nicht sagen können, was ein Elektron letztlich tatsächlich ist (wir also nichts über seine Qualität sagen können), so ist es aber dieses "Etwas", über das unsere Modelle Aussagen machen.
Henry�
Beitrag 1896-64
-
Mir wird jetzt erst klar, dass man allzu oft selbst da noch » physikalisch « sagt, wo man » physisch « meint.
Daher sei klargestellt:
Henry in 1896-20:Grtgrt in 1896-19:
Henry und Harti,
die Tatsache, dass ihr — anders als ich — den Begriff "physikalisches Objekt" als Synonym für "ein Teil der Natur" seht, zeigt mir, dass ich in Zukunft wohl besser von physikalischen Modellen (statt Objekten) sprechen sollte.
Ein Elektron, aber z.B. auch ein ganzes Universum, wären dann also stets zu verstehen als ein Teil der Natur, dessen Verhalten wir zu beschreiben suchen über ein oder mehrere — gleichwertige oder einander ergänzende — Modelle.
Danke & Gruß,
grtgrt
Hallo, Gebhard,
wir kommen der Sache langsam näher! Ich kann nur für mich sprechen: Mit einem "physikalischen Objekt" meine ich einen quantifizierbaren, also messbaren Teil der Natur und nicht das Modell davon. (Dass sich die Physik nun mit den messbaren Eigenschaften ihrer Objekte befasst, ist natürlich nicht meine Idee.)
Die "physikalischen Objekte " sind auch Teil der Natur, aber nicht einfach "Synonym für Teil der Natur". Ein Mensch (ein Lebewesen) ist ein physikalisches Objekt, aber wer will behaupten, es würde mit einer physikalischen Beschreibung vollständig erfasst sein? Objekte der Natur sind mehr als quantifizierbare Einheiten, sie "sind" auch und vor allen Dingen Qualität, und die lässt sich nicht messen. Ein Elektron z. B. ist ein physikalisches Objekt, über das wir nur in Modellen aufgrund von Messungen etwas aussagen können. Wenn wir auch nicht sagen können, was ein Elektron letztlich tatsächlich ist (wir also nichts über seine Qualität sagen können), so ist es aber dieses "Etwas", über das unsere Modelle Aussagen machen.
Henry
Mir wird jetzt erst klar, dass man allzu oft selbst da noch » physikalisch « sagt, wo man » physisch « meint.
Daher sei klargestellt:
- Ein physisches Objekt ist ein nicht nur in Gedanken existierender Teil unserer Welt (oder des Kosmos).
- Ein physikalisches Objekt dagegen ist ein durch Physiker diskutiertes Modell eines physischen Objekts (oder einer Klasse physischer Objekte).
Beitrag 1896-65
-
Gebhard, wenn ich "physikalisch" sage, meine ich auch "physikalisch", nämlich "zur Physik gehörend", und die Physik ist die "wissenschaftliche Beschäftigung mit den Naturerscheinungen" (Zitat aus Wikipedia).
"physich" meint: körperlich im Gegensatz zum geistigen; die Natur betreffend im Gegensatz zum Metaphysischen, also "über die Natur hinausgehend"; das Körperliche betreffend, z. B. synonym zu "somatisch"; allgemein zur Natur gehörend.�
Grtgrt in 1896-64:
Mir wird jetzt erst klar, dass man allzu oft selbst da noch » physikalisch « sagt, wo man » physisch « meint.
Daher sei klargestellt:Ein physisches Objekt ist ein nicht nur in Gedanken existierender Teil unserer Welt (oder des Kosmos).
Ein physikalisches Objekt dagegen ist ein durch Physiker diskutiertes Modell eines physischen Objekts (oder einer Klasse physischer Objekte).
Gebhard, wenn ich "physikalisch" sage, meine ich auch "physikalisch", nämlich "zur Physik gehörend", und die Physik ist die "wissenschaftliche Beschäftigung mit den Naturerscheinungen" (Zitat aus Wikipedia).
"physich" meint: körperlich im Gegensatz zum geistigen; die Natur betreffend im Gegensatz zum Metaphysischen, also "über die Natur hinausgehend"; das Körperliche betreffend, z. B. synonym zu "somatisch"; allgemein zur Natur gehörend.�
Beitrag 1896-66
-
Hallo Henry,
hat man deinen Beitrag 1896-65 so zu verstehen, dass Du jetzt doch mit mir der Meinung bist, dass gilt:
Gruß, grtgrt
Hallo Henry,
hat man deinen Beitrag 1896-65 so zu verstehen, dass Du jetzt doch mit mir der Meinung bist, dass gilt:
- physisch = wie das Objekt in der Natur existiert
- physikalisch = wie der Physiker das Objekt sieht (und wie er es demnach auch modelliert)?
Gruß, grtgrt
Beitrag 1896-21
Platon oder Aristoteles - wer hatte recht?
Einige Tatsachen, diese Meinung zu begründen, habe ich oben in Beitrag 1896-4 schon genannt.
Noch viel interessanter aber finde ich, dass offenbar schon Platon dieser Meinung war: Max Tegmark — Professor für Physik am MIT — schreibt in Spalte 2 auf Seite 12 eines Papiers, in dem er Ideen für potentiell existierende Parallel-Universen zusammenträgt und klassifiziert folgendes:
Nebenbei: Dass auch Aristoteles nicht falsch liegt, erkennt sofort, wer sich klar macht, dass mathematische Sprache nur Methodik darstellt und jedes Modell, auch wenn es mathematisch aufgebaut ist, ja noch keineswegs wirklich in jeder Hinsicht isomorph zur Natur sein muss.
In anderen Worten: Der von Tegmark gesehene Widerspruch zwischen den Meinungen von Platon und Aristoteles verschwindet, wenn man meiner Deutung des Wesens der Mathematik folgt: Sie ist ein Paar bestehend aus
grtgrt
Grtgrt aus 1896-1:Mathematische Gesetze sind Teil der Natur
und Mathematik kann als der Teil der Physik verstanden werden, der diesen Teil der Natur entdeckt
und diskutierbar macht (modelliert).
Einige Tatsachen, diese Meinung zu begründen, habe ich oben in Beitrag 1896-4 schon genannt.
Noch viel interessanter aber finde ich, dass offenbar schon Platon dieser Meinung war: Max Tegmark — Professor für Physik am MIT — schreibt in Spalte 2 auf Seite 12 eines Papiers, in dem er Ideen für potentiell existierende Parallel-Universen zusammenträgt und klassifiziert folgendes:
Zitat von Max Tegmark, MIT:
There are two tenable but diametrically opposed paradigms regarding physical reality and the status of mathematics, a dichotomy that arguably goes as far back as Plato and Aristotle, and the question is which one is correct.
- ARISTOTELIAN PARADIGM: The subjectively perceived frog perspective is physically real, and the bird perspective and all its mathematical language is merely a useful approximation.
- PLATONIC PARADIGM: The bird perspective (the mathematical structure) is physically real, and the frog perspective and all the human language we use to describe it is merely a useful approximation for describing our subjective perceptions. What is more basic — the frog perspective or the bird perspective? What is more basic — human language or mathematical language?
Nebenbei: Dass auch Aristoteles nicht falsch liegt, erkennt sofort, wer sich klar macht, dass mathematische Sprache nur Methodik darstellt und jedes Modell, auch wenn es mathematisch aufgebaut ist, ja noch keineswegs wirklich in jeder Hinsicht isomorph zur Natur sein muss.
In anderen Worten: Der von Tegmark gesehene Widerspruch zwischen den Meinungen von Platon und Aristoteles verschwindet, wenn man meiner Deutung des Wesens der Mathematik folgt: Sie ist ein Paar bestehend aus
- Naturgesetzen einerseits
- und des Menschen präzisester Methodik sie zu formulieren andererseits.
grtgrt
Beitrag 1896-25
Beide hatten recht
Hallo Grtgrt,
ich stimme Dir im Prinzip zu, würde aber als "Mathematik" nur den zweiten Teil des von Dir genannten Paares auffassen wollen.
Wenn man die Trennung objektiv existierende Welt (Natur, Wirklichkeit, naturgesetzliche Geschehensabläufe etc) und Denken (Vorstellung, Bewußtsein, Theorien etc.) für zweckmäßig hält, ist die Mathematik unser päzisestes und widerspruchfreies System zur Beschreibung und Erfassung der Natur.
Demgegenüber sind andere Systeme wie Sprache (Bilder) mit Mängeln behaftet, die insbesondere in der Ungenauigkeit der begrifflichen Inhalte bestehen und deshalb häufig zu Missverständnissen führen. Allerdings ist die Mathematik ein Spezialsystem, das von der Mehrheit der Menschen, auch von mir, nur sehr begrenzt (teilweise) verstanden wird. (Auch Einstein soll sich für die mathematische Formulierung seiner Allgemeinen Relativitätstheorie Hilfe geholt haben).
Allerdings ist auch bei der Beschreibung der Natur mit Hilfe der Mathematik Vorsicht geboten, insbesondere wenn Unendlichkeiten auftauchen. Beispielsweise kann man mit Hilfe von Grenzwertbetrachtungen eine Momentangeschwindigkeit angeben, was nichts anderes bedeutet, als dass man die Beziehung Strecke/Zeit auf eine Strecke mit der Länge 0 und eine Zeit mit der Dauer 0 zueinander in Beziehung setzt. Eine Bewegung, die über 0 Meter erfolgt, ist aber keine Bewegung mehr, sondern bedeutet in unserer sprachlichen Beschreibung "Ruhe". Ich bin der Meinung, dass die Unschärferelation (Ort und Geschwindigkeit eines Elementarteilchens können nicht gleichzeitig mit beliebiger Genauigkeit festgestellt werden) hierin begründet ist.
Dies wird auch deutlich,wenn man die Bewegung von Teilchen im Rahmen der vierdimensionalen Raumzeit betrachtet. Hier gibt es keine "Ruhe" im herkömmlichen Sinn, allenfalls Bewegung nur in der Zeit (geometrisch auf der Zeitachse). Eine Unterscheidung zwischen Ort (Ruhe) und Geschwindigkeit (Bewegung) ist nur in dem Sinne möglich, dass sich ein Objekt mit Lichtgeschwindigkeit allein in der Zeit bewegt (im herkömmlichen Sinn räumlich ruht) oder mit Lichtgeschwindikeit sich teilweise in der Zeit und teilweise im Raum bewegt (im herkömmlichen Sinn in räumlicher Bewegung ist). Die Unschärferelation verliert deshalb nach meiner Auffassung, auf der Grundlage der vierdimensionalen Raumzeit betrachtet, ihre Bedeutung.
MfG
Harti�
Grtgrt aus 1896-21:
In anderen Worten: Der von Tegmark gesehene Widerspruch zwischen den Meinungen von Platon und Aristoteles verschwindet, wenn man meiner Deutung des Wesens der Mathematik folgt: Sie ist ein Paar bestehend aus
- Naturgesetzen einerseits
- und des Menschen präzisester Methodik sie zu formulieren andererseits.
Hallo Grtgrt,
ich stimme Dir im Prinzip zu, würde aber als "Mathematik" nur den zweiten Teil des von Dir genannten Paares auffassen wollen.
Wenn man die Trennung objektiv existierende Welt (Natur, Wirklichkeit, naturgesetzliche Geschehensabläufe etc) und Denken (Vorstellung, Bewußtsein, Theorien etc.) für zweckmäßig hält, ist die Mathematik unser päzisestes und widerspruchfreies System zur Beschreibung und Erfassung der Natur.
Demgegenüber sind andere Systeme wie Sprache (Bilder) mit Mängeln behaftet, die insbesondere in der Ungenauigkeit der begrifflichen Inhalte bestehen und deshalb häufig zu Missverständnissen führen. Allerdings ist die Mathematik ein Spezialsystem, das von der Mehrheit der Menschen, auch von mir, nur sehr begrenzt (teilweise) verstanden wird. (Auch Einstein soll sich für die mathematische Formulierung seiner Allgemeinen Relativitätstheorie Hilfe geholt haben).
Allerdings ist auch bei der Beschreibung der Natur mit Hilfe der Mathematik Vorsicht geboten, insbesondere wenn Unendlichkeiten auftauchen. Beispielsweise kann man mit Hilfe von Grenzwertbetrachtungen eine Momentangeschwindigkeit angeben, was nichts anderes bedeutet, als dass man die Beziehung Strecke/Zeit auf eine Strecke mit der Länge 0 und eine Zeit mit der Dauer 0 zueinander in Beziehung setzt. Eine Bewegung, die über 0 Meter erfolgt, ist aber keine Bewegung mehr, sondern bedeutet in unserer sprachlichen Beschreibung "Ruhe". Ich bin der Meinung, dass die Unschärferelation (Ort und Geschwindigkeit eines Elementarteilchens können nicht gleichzeitig mit beliebiger Genauigkeit festgestellt werden) hierin begründet ist.
Dies wird auch deutlich,wenn man die Bewegung von Teilchen im Rahmen der vierdimensionalen Raumzeit betrachtet. Hier gibt es keine "Ruhe" im herkömmlichen Sinn, allenfalls Bewegung nur in der Zeit (geometrisch auf der Zeitachse). Eine Unterscheidung zwischen Ort (Ruhe) und Geschwindigkeit (Bewegung) ist nur in dem Sinne möglich, dass sich ein Objekt mit Lichtgeschwindigkeit allein in der Zeit bewegt (im herkömmlichen Sinn räumlich ruht) oder mit Lichtgeschwindikeit sich teilweise in der Zeit und teilweise im Raum bewegt (im herkömmlichen Sinn in räumlicher Bewegung ist). Die Unschärferelation verliert deshalb nach meiner Auffassung, auf der Grundlage der vierdimensionalen Raumzeit betrachtet, ihre Bedeutung.
MfG
Harti�
Beitrag 1896-22
Natur und Primzahlen
Hallo Gebhard,
Es könnte allerdings sein, dass die universelle Sprache der Natur wirklich Mathematik ist, und reine Mathematik nichts von Menschen Erdachtes (sondern "nur" Erkanntes), sondern vielmehr der Bauplan des Universums ist:
http://www.3sat.de/mediathek/?display=1&mode=pl...
(Hallo Leute, dieser Link verweist auf einen Film, der ca. 45 min lang ist. Also plant entsprechend Zeit und Muße ein. Von mir allerdings kann ich behaupten, dass mich der Inhalt umgehauen hat.)
Dir, Gebhard, dürfte vieles in diesem Film nicht fremd sein, aber vielleicht lohnt er auch für dich.
Grüße
Grtgrt aus 1896-21:...dass mathematische Sprache nur Methodik darstellt und jedes Modell, auch wenn es mathematisch aufgebaut ist, ja noch keineswegs wirklich in jeder Hinsicht isomorph zur Natur sein muss.
Es könnte allerdings sein, dass die universelle Sprache der Natur wirklich Mathematik ist, und reine Mathematik nichts von Menschen Erdachtes (sondern "nur" Erkanntes), sondern vielmehr der Bauplan des Universums ist:
http://www.3sat.de/mediathek/?display=1&mode=pl...
(Hallo Leute, dieser Link verweist auf einen Film, der ca. 45 min lang ist. Also plant entsprechend Zeit und Muße ein. Von mir allerdings kann ich behaupten, dass mich der Inhalt umgehauen hat.)
Dir, Gebhard, dürfte vieles in diesem Film nicht fremd sein, aber vielleicht lohnt er auch für dich.
Grüße
Beitrag 1896-26
Begriffsverwirrung
Hi Harti,
da die Naturgesetze in dem Paar, von dem ich spreche, mathematische Gesetzmäßigkeiten sind, fällt es mir schwer, sie nicht der Mathematik zuzurechnen.
Im Prinzip aber hast du recht: Man könnte den Begriff Mathematik so definieren, dass damit nur des Menschen Methodik gemeint ist, jene Naturgesetze (mathematischer Art) zu formulieren, zu entdecken, und praktischer Anwendung zugänglich zu machen.
Gruß, grtgrt
Hi Harti,
da die Naturgesetze in dem Paar, von dem ich spreche, mathematische Gesetzmäßigkeiten sind, fällt es mir schwer, sie nicht der Mathematik zuzurechnen.
Im Prinzip aber hast du recht: Man könnte den Begriff Mathematik so definieren, dass damit nur des Menschen Methodik gemeint ist, jene Naturgesetze (mathematischer Art) zu formulieren, zu entdecken, und praktischer Anwendung zugänglich zu machen.
Gruß, grtgrt
Beitrag 1896-53
Das Credo von Lothar Schäfer (einem Physiker)
Das Credo von Lothar Schäfer — einem Physiker:
Er sagt ferner:
Transzendente Wirklichkeit ist ihrem Wesen nach unbeobachtbar.
Die moderne Physik ist in zunehmendem Maße bereit, sie zur Erklärung der Wirklichkeit dennoch zuzulassen.
Die Botschaft moderner Physik ist, dass die Wirklichkeit an ihren Grenzen nicht im Nichts verklingt, sondern im Bereich des Metaphysischen.
Das Credo von Lothar Schäfer — einem Physiker:
- An der Wurzel der physikalischen Wirklichkeit erweist sich die Natur der materiellen Dinge als nicht-materiell.
- Örtliche Ordnung wird durch nicht-lokale, unverzögert fernwirksame Phänome beeinflusst.
- Die Wirklichkeit der Raumzeit hängt möglicherweise von Prozessen ab, die außerhalb der Raumzeit verankert sind.
Er sagt ferner:
Die moderne Physik ist in zunehmendem Maße bereit, sie zur Erklärung der Wirklichkeit dennoch zuzulassen.
Die Botschaft moderner Physik ist, dass die Wirklichkeit an ihren Grenzen nicht im Nichts verklingt, sondern im Bereich des Metaphysischen.
Beitrag 1896-55
Besteht unsere Welt wirklich nur aus der Raumzeit und dem darin Vorhandenen?
Hallo H...,
Beste Grüße,
grtgrt
Hallo H...,
- konkretes, anerkanntes (und einziges mir bekanntes) Beispiel für "unverzögert fernwirksame Phänomene" ist das Phänomen der Quantenverschränkung.
- Was Prozesse angeht, die außerhalb der Raumzeit ablaufen, so sehe auch ich keinerlei Hinweise darauf.
- Ich sehe aber sehr wohl Anzeichen dafür, dass unsere Welt nicht nur aus der Raumzeit bestehen könnte, sondern darüber hinaus eine bisher noch nicht identifizierte zusätzliche transzendente Dimension haben muss: Eine Art Schema, welches die Naturgesetze darstellt, die Regeln also, die bestimmen, an welche Randbedingungen sich alles andere — die Raumzeit und alles, was darin existiert — zu halten hat. Etwas mehr dazu in Beitrag 1915-7.
Beste Grüße,
grtgrt
Beitrag 1904-17
Materielle und vermeintliche Wirklichkeit
Der 3D Film auf der Kinoleinwand ist real als auf die Leinwand fallendes List. Er ist auch real als Geschichte, die erzählt wird.
Wer aber möchte behaupten, dass, was er erzählt, notwendigerweise Wirklichkeit darstellt?
Hans-m aus 1904-16:Okotombrok aus 1904-8:Wirklichkeit ist für mich alles, was mit meinen Sinnesorganen incl. Hilfsmitteln wie Brille und Teilchenbeschleunigern wechselwirkt.
Copperfield´s Verschwinden aus dem Käfig wechselwirkt auch mit deinen Sinnen und ebenfalls der 3D Film auf der Kino-Leinwand,
aber kannst Du das als Wirklichkeit definieren?
- Was Okotombrok als Wirklichkeit definiert, ist materielle Wirklichkeit.
- Copperfield's Verschwinden aber ist vermeintliche Wirklichkeit.
Wer aber möchte behaupten, dass, was er erzählt, notwendigerweise Wirklichkeit darstellt?
Beitrag 1904-20
Heisenbergs Antwort: auch Potentia ist existentes Ding
Diese Meinung, Okotombrok, teile ich nicht.
Heisenbergs Potentia scheinen mir ganz klar die Zustände zu sein, die eintreten k ö n n e n , also irgendwie schon vorgedacht und möglich gemacht sind.
In seinem Buch "Versteckte Wirklichkeit" (Hirzel, 2004) sieht Lothar Schäfer das ebenso und schreibt:
"Das einfachste Beispiel ist ein Wasserstoffatom. Wenn es in seinem Grundzustand ist – chemisches Symbol 1s – dann muss man annehmen, dass die Zustände höherer Energie – allgemein mit den Symbolen 2s, 3s, 3p usw. bezeichnet – in diesem Atom auch existieren, obgleich sie leer und daher nicht in einem materiellen Sinn wirklich sind.
... Sie existieren wie mathematische Formen, Ordnungsmuster oder wie Information, aber sie sind mehr als nur die I d e e einer solchen Form, weil sie wirklich betreten werden können. ...
... Zwar wird der Akt des Springens von einem Quantenzustand in einen anderen vom Zufall bestimmt, aber das gilt nicht für die Ordnung des Zustandes, der so erreicht wird:
Blinder Zufall kann zu Allem führen, ob er aber auch erschafft, wohin er führt, ist eine völlig andere Frage."
Beste Grüße,
grtgrt
Okotombrok aus 1904-19:Hallo Grtgrt,
Grtgrt aus 1904-15:Auch Heisenberg hat sich darin versucht, zu definieren, was wirklich ist und existiert: Er spricht von Objekten und Zuständen, die
"als Potentia in einer seltsamen Wirklichkeit zwischen der Idee von einem Ding und einem wirklichen Ding existieren".
ich verstehe Heisenberg eher so, dass mit "Potentia" und "der Idee von einem Ding" die Zukunft gemeint ist. Sie bedeutet Möglichkeiten, noch nicht entschieden, unbestimmt im Rahmen von Wahrscheinlichkeiten (Unbestimmtheitsrelation), im Gegensatz zur klassischen Mechanik, bei der die Zukunft determiniert ist.
Mit dem "wirklichen Ding" meint er etwas, was wechselgewirkt hat, was zum Faktum wurde und von dem wir prinzipiell wissen können – Vergangenheit.
Diese Meinung, Okotombrok, teile ich nicht.
Heisenbergs Potentia scheinen mir ganz klar die Zustände zu sein, die eintreten k ö n n e n , also irgendwie schon vorgedacht und möglich gemacht sind.
In seinem Buch "Versteckte Wirklichkeit" (Hirzel, 2004) sieht Lothar Schäfer das ebenso und schreibt:
"Das einfachste Beispiel ist ein Wasserstoffatom. Wenn es in seinem Grundzustand ist – chemisches Symbol 1s – dann muss man annehmen, dass die Zustände höherer Energie – allgemein mit den Symbolen 2s, 3s, 3p usw. bezeichnet – in diesem Atom auch existieren, obgleich sie leer und daher nicht in einem materiellen Sinn wirklich sind.
... Sie existieren wie mathematische Formen, Ordnungsmuster oder wie Information, aber sie sind mehr als nur die I d e e einer solchen Form, weil sie wirklich betreten werden können. ...
... Zwar wird der Akt des Springens von einem Quantenzustand in einen anderen vom Zufall bestimmt, aber das gilt nicht für die Ordnung des Zustandes, der so erreicht wird:
Blinder Zufall kann zu Allem führen, ob er aber auch erschafft, wohin er führt, ist eine völlig andere Frage."
Beste Grüße,
grtgrt
Beitrag 1904-22
Dinghafte Wirklichkeit existiert nur als Abstraktion (als Wahrnehmung also)
Hans-Peter-Dürr, schreibt in seinen Reflexionen einen Quantenphysikers:
Hans-Peter-Dürr, schreibt in seinen Reflexionen einen Quantenphysikers:
Zitat:Der Bruch, den die neue [mit der Quantenmechanik beginnende] Physik fordert, ist tief. Deutet diese Physik doch darauf hin, daß
die Wirklichkeit, was immer wir darunter verstehen, im Grunde keine Realität im Sinne einer dinghaften Wirklichkeit ist.
Wirklichkeit offenbart sich primär nurmehr als Potentialität, als ein "Sowohl-als-auch" ...
Beitrag 1904-29
Real und gleichzeitig nicht real zu sein, schließen einander NICHT aus
Das, Thomas, sehe ich durchaus ebenso,
denn wenn ich z.B. an Platons Höhlengleichnis denke, so sind dort ja die Schatten an der Wand (als Schatten) ebenso real, wie Gegenstände, die jene Schatten werfen.
Was wir meinen, wenn wir von mehr oder weniger Realem sprechen, ist also stets
Man kann es auch so sagen:
Wo wir uns fragen, ob ein Ding X real ist, fragen wir danach, ob der Betrachter es in der richtigen Rolle als real sieht.
Bezogen auf Platons Höhlengleichnis etwa wäre der Schatten einer Ziege, den Gefangene an der Wand der Höhle sehen, für sie
Gruß, grtgrt
Thomas der Große aus 1904-28:Alles ist real
Das, Thomas, sehe ich durchaus ebenso,
denn wenn ich z.B. an Platons Höhlengleichnis denke, so sind dort ja die Schatten an der Wand (als Schatten) ebenso real, wie Gegenstände, die jene Schatten werfen.
Was wir meinen, wenn wir von mehr oder weniger Realem sprechen, ist also stets
- entweder die Frage, welche Realität denn nur Folge welcher anderen ist (eine Ordnung auf der Menge aller Realitäten also)
- oder einfach nur die Frage, was uns aufgrund welcher gedanklichen Fehler als real erscheinen mag (ohne dass es wirklich existiert): Ein amputiertes Bein etwa, das dem Patienten immer noch über Phantomschmerz als vorhanden erscheint, ist nun mal nicht mehr real — real ist in dem Fall nur der Schmerz.
Man kann es auch so sagen:
Wo wir uns fragen, ob ein Ding X real ist, fragen wir danach, ob der Betrachter es in der richtigen Rolle als real sieht.
Bezogen auf Platons Höhlengleichnis etwa wäre der Schatten einer Ziege, den Gefangene an der Wand der Höhle sehen, für sie
- als REAL einzustufen, wenn ihnen bewusst wäre, dass, was sie sehen, nur ein Schatten ist,
- als NICHT REAL aber, wenn sie eben diesen Schatten für das eigentliche Ding X halten (in diesem Fall eine Ziege).
Gruß, grtgrt
Beitrag 1904-31
Realität ist nur in bestimmter Rolle wirklich Reales
Hi Thomas,
was ich ausdrücken wollte war: Es gibt eine transzendente (d.h. durch uns unverstandene, oder noch unverstandene) Wirklichkeit.
Wo wir über sie nachdenken, kann solches Nachdenken aber nur zum Ziel haben, Teile davon zu verstehen.
Zum Maßstab aller Überlegungen darf man sie auf keinen Fall machen, denn wo man ohne Not auf noch Unverstandenem aufbaut, kann sich eigentlich keinerlei Beweis mehr ergeben. Von logischem Vorgehen hätte man sich dann verabschiedet.
In Bezug auf verschiedene Realitäten sei festgestellt:
Wo immer uns etwas begegnet, das wir versucht sind als Realität zu sehen, sollten wir uns bewusst fragen, was die ihr zugeordnete Rolle ist.
Wo die nämlich nicht richtig erkannt wird, ist man auf dem Holzweg: Der Schatten einer Ziege gibt z.B. keine Milch, und aufessen kann man ihn auch nicht.
Mit dieser Aussage kann ich ehrlich gesagt rein gar nichts anfangen.
Gruß, grtgrt
Thomas der Große aus 1904-30:Hallo Grtgrt,
Du hast oben von einer transzendenten Wirklichkeit gesprochen, die man sinnvollerweise annimmt.
Die wird man zum Masstab für alle Schattenspiele machen.
Hi Thomas,
was ich ausdrücken wollte war: Es gibt eine transzendente (d.h. durch uns unverstandene, oder noch unverstandene) Wirklichkeit.
Wo wir über sie nachdenken, kann solches Nachdenken aber nur zum Ziel haben, Teile davon zu verstehen.
Zum Maßstab aller Überlegungen darf man sie auf keinen Fall machen, denn wo man ohne Not auf noch Unverstandenem aufbaut, kann sich eigentlich keinerlei Beweis mehr ergeben. Von logischem Vorgehen hätte man sich dann verabschiedet.
In Bezug auf verschiedene Realitäten sei festgestellt:
Wo immer uns etwas begegnet, das wir versucht sind als Realität zu sehen, sollten wir uns bewusst fragen, was die ihr zugeordnete Rolle ist.
Wo die nämlich nicht richtig erkannt wird, ist man auf dem Holzweg: Der Schatten einer Ziege gibt z.B. keine Milch, und aufessen kann man ihn auch nicht.
Thomas der Große aus 1904-30:Die Quantentheorie ist per Definition ein Schattenspiel, weil sie ihren Zufallsgenerator nicht kennt.
Mit dieser Aussage kann ich ehrlich gesagt rein gar nichts anfangen.
Gruß, grtgrt
Beitrag 1913-4
Wie man erkennt, dass die Grundlage der materiellen Welt nicht-materiell ist
Wie in Beitrag 1913-3 gezeigt, wird Evolution durch zweierlei Zufall gesteuert:
Es ist wichtig, zu sehen, dass der hintergründige den vordergründigen kanalisiert, selbst aber auch kanalisiert wird durch die den Quanten zugeordneten Wahrscheinlichkeitswellen (durch das also, was Heisenberg als die der kosmischen Ordnung zugrundeliegenden " Tendenzen und Neigungen" nennt: siehe Beitrag 1915-5).
Da nun aber Wahrscheinlichkeiten nichts anderes als dimensionslose Zahlenverhältnisse sind, kommt man nicht umhin, feststellen zu müssen:
Wem das zu abstrakt ist, der sollte sich vor Augen führen, dass man — ausgehend von der Kenntnis der den Quanten zugeordneten Wahrscheinlichkeitswellen — die Struktur von Molekülen berechnen kann, letztlich also die Gesetze der Chemie.
Wie weit man da heute schon ist, weiß ich nicht genau. Auf jeden Fall gilt:
Alle Moleküle, ob groß oder klein, sind Quantensysteme,
und so wirkt der quantenphysikalische Zufall hinein in sämtliche chemikalischen Vorgänge (!).
Das ist für die Evolution durchaus bedeutsam, wenn man sich vor Augen führt, dass quantenphysikalischer Zufall ja nur bezogen auf das Ergebnis je eines einzelnen Ereignisses absoluter Zufall zu sein scheint, statistisch gesehen aber, wie oben gerade erklärt, durchaus kanalisierend wirkt.
grtgrt
PS: Zur Terminologie, den Zufall betreffend, siehe Beitrag 1911-1.
Wie in Beitrag 1913-3 gezeigt, wird Evolution durch zweierlei Zufall gesteuert:
- durch einen vordergründig wirkenden (das ist der, von dem Darwin und die Beispiele aus Beitrag 1913-2 sprechen),
- daneben aber auch durch einen hintergründig wirkenden (das ist der quantenphysikalische).
Es ist wichtig, zu sehen, dass der hintergründige den vordergründigen kanalisiert, selbst aber auch kanalisiert wird durch die den Quanten zugeordneten Wahrscheinlichkeitswellen (durch das also, was Heisenberg als die der kosmischen Ordnung zugrundeliegenden " Tendenzen und Neigungen" nennt: siehe Beitrag 1915-5).
Da nun aber Wahrscheinlichkeiten nichts anderes als dimensionslose Zahlenverhältnisse sind, kommt man nicht umhin, feststellen zu müssen:
Zitat von Lothar Schäfer in: Versteckte Wirklichkeit, S. 47:An der Wurzel der Wirklichkeit finden wir Zahlenverhältnisse — nichtmaterielle Prinzipien, auf denen die Ordnung dieser Welt gegründet ist.
Die Grundlage der materiellen Welt ist somit nichtmateriell.
Wem das zu abstrakt ist, der sollte sich vor Augen führen, dass man — ausgehend von der Kenntnis der den Quanten zugeordneten Wahrscheinlichkeitswellen — die Struktur von Molekülen berechnen kann, letztlich also die Gesetze der Chemie.
Wie weit man da heute schon ist, weiß ich nicht genau. Auf jeden Fall gilt:
- Schon 1998 gelang es, die Struktur von Cambrin zu berechnen. Cambrin ist mit etwa 640 Atomen ein eher kleines Protein-Molekül. Über noch größere Erfolge berichten Treppen et al., 2002, J. Phys. Chem. A. 106; 5498-5503.
- Insbesondere weiß man: Die Struktur selbst der größten röntgenographisch erforschten Proteine kann durch quanten-chemische Berechnungen ihrer Teile vorhergesagt werden (Jiang et al., 1995, Phys. Chem. 99:10521).
und so wirkt der quantenphysikalische Zufall hinein in sämtliche chemikalischen Vorgänge (!).
Das ist für die Evolution durchaus bedeutsam, wenn man sich vor Augen führt, dass quantenphysikalischer Zufall ja nur bezogen auf das Ergebnis je eines einzelnen Ereignisses absoluter Zufall zu sein scheint, statistisch gesehen aber, wie oben gerade erklärt, durchaus kanalisierend wirkt.
grtgrt
PS: Zur Terminologie, den Zufall betreffend, siehe Beitrag 1911-1.
Beitrag 1923-1
Gibt es physikalisches Modelle, die beliebig weit ins Ultra-mikroskopische hinein Sinn machen?
Warum wir stets nur eine makroskopische Sicht auf die Natur haben können
Wo man die Energie eines Quantums (z.B. eines Elektrons oder eines Photons) zu messen sucht, muss man — so wird mir glaubhaft versichert — Energie und Zeit als zueinander konjugierte Größen im Sinne von Heisenbergs Unschärferelation betrachten. Damit gilt die Ungleichung
Δ
E Δ
t ≥
h/4π
wo h das Plancksche Wirkungsquantum bezeichnet (eine positive Zahl, die man als Naturkonstante kennt).
Nach gängiger Interpretation beschreibt diese Ungleichung nun aber keineswegs nur eine Unschärfe der Beobachtung, sondern vielmehr auch eine der Natur selbst innewohnende Unschärfe. Wer nun Δ t zunehmend kleiner wählt, erkennt,
dass mindestens eine der folgenden Thesen wahr sein muss:
Welche auch immer wahr sein sollte, man kann auf jeden Fall mit Sicherheit behaupten:
Es gibt eine (ultra-) mikroskopische Sicht auf die Natur, in der mindestens eine der Größen Zeit bzw. Energie keinen Sinn mehr macht.
Sie macht also nur Sinn aus makroskopischer Sicht.
Das aber lässt mich fragen:
Gibt es denn überhaupt ein physikalisches Modell, welches beliebig weit ins Ultra-mikroskopische hinein Sinn macht?
Letztlich führt das auch auf die Frage, in welchem Ausmaß Elementarteilchen denn überhaupt als "existierend" bezeichnet werden können.
Heisenberg selbst noch hat das klar erkannt, denn auf Seite 101 seines Buches "Physics and Philosophie" (1958) liest man:
Gebhard Greiter (grtgrt)
Wo man die Energie eines Quantums (z.B. eines Elektrons oder eines Photons) zu messen sucht, muss man — so wird mir glaubhaft versichert — Energie und Zeit als zueinander konjugierte Größen im Sinne von Heisenbergs Unschärferelation betrachten. Damit gilt die Ungleichung
wo h das Plancksche Wirkungsquantum bezeichnet (eine positive Zahl, die man als Naturkonstante kennt).
Nach gängiger Interpretation beschreibt diese Ungleichung nun aber keineswegs nur eine Unschärfe der Beobachtung, sondern vielmehr auch eine der Natur selbst innewohnende Unschärfe. Wer nun Δ t zunehmend kleiner wählt, erkennt,
- These 1: Es gibt kleinste Zeitspannen (die Zeit ist also gequantelt).
- These 2: In jeder noch so kleinen Zeitspanne wächst die Energie des Quantums unendlich oft über jede nur denkbare Grenze.
- These 3: In jeder noch so kleinen Zeitspanne hört das Quantum unendlich oft auf zu existieren.
Sie macht also nur Sinn aus makroskopischer Sicht.
Das aber lässt mich fragen:
Letztlich führt das auch auf die Frage, in welchem Ausmaß Elementarteilchen denn überhaupt als "existierend" bezeichnet werden können.
Heisenberg selbst noch hat das klar erkannt, denn auf Seite 101 seines Buches "Physics and Philosophie" (1958) liest man:
Zitat von Heisenberg:Wenn man eine genaue Beschreibung des Elementarteilchens geben will ... erkennt man, dass nicht einmal die Eigenschaft des "Seins"
— wenn man hier überhaupt von einer Eigenschaft reden will —
dem Elementarteilchen ohne Einschränkung zukommt.
Gebhard Greiter (grtgrt)
Beitrag 2085-287
Die Natur zu beobachen bedeutet, sie zu verändern
Hallo Okotombrok,
was ich da geschrieben hatte, klingt zwar vielleicht philosophisch, sollte es aber nicht sein. Ich hatte etwas anderes im Sinn als Philosophie:
Das Quanten-Geschehen ist gekennzeichnet durch die Heisenbergsche Unbestimmtheitsrelation. Wenn wir messen, kommt noch ein unbestimmbarer Eingriff durch den Messvorgang hinzu, der die vermeintliche Realität zusätzlich verschleiert. Deshalb ist für uns als Beobachter unmöglich, eine (vermeintlich) vorhandene wahre Realität zu erkennen, weil wir und unsere Messinstrumente Teil des Universums sind. Bei jedem Messvorgang ist der Beobachter mit seiner speziellen Art des Messens am Messergebnis beteiligt. Messobjekte, Messinstrumente und Beobachter sind eine untrennbare Einheit.
Und weil dem so ist, können wir nie die Realität in ihrem Wesen erkennen. Wir können nicht vom Messinstrument abstrahieren. Deshalb ist das für uns Realität, was die Messinstrumente anzeigen. Eine dahinter stehende "wahre" Realität ist uns prinzipiell unzugänglich, wenn sie denn überhaupt gegeben ist. Die Quantentheorie verneint eine dahinterstehende Realität.
M.f.G. Eugen Bauhof�
Okotombrok in 2085-283:Bauhof in 2085-278:gerade darum, weil wir Teil der Realität sind, können wir nie die Realität in ihrem Wesen erkennen. Unsere Realität ganz zu überblicken, könnte nur ein Wesen, das außerhalb unserer Realität steht.
das ist wohl richtig.
Wir sind aber nicht Teil der Natur in dem Sinne, wie ein Wassertropfen Teil eines Ozeans ist. Zunächst sind wir Individuen und als solche getrennt von der Umwelt zu sehen. Das macht ein Individuum aus.
Gleichwohl können wir nicht erkennen, was die Natur an sich ist. Wir können nur eine Natur erkennen, wie sie sich unserer Fragestellung zeigt. Und die Antworten die wir erhalten verstehen wir immer nur im Vergleich mit anderen Antworten. Messen heißt Vergleichen, wie wir es in der Schule gelernt haben, und die Bedeutung dieses Satzes ist mir erst viel später bewusst geworden.
Hallo Okotombrok,
was ich da geschrieben hatte, klingt zwar vielleicht philosophisch, sollte es aber nicht sein. Ich hatte etwas anderes im Sinn als Philosophie:
Das Quanten-Geschehen ist gekennzeichnet durch die Heisenbergsche Unbestimmtheitsrelation. Wenn wir messen, kommt noch ein unbestimmbarer Eingriff durch den Messvorgang hinzu, der die vermeintliche Realität zusätzlich verschleiert. Deshalb ist für uns als Beobachter unmöglich, eine (vermeintlich) vorhandene wahre Realität zu erkennen, weil wir und unsere Messinstrumente Teil des Universums sind. Bei jedem Messvorgang ist der Beobachter mit seiner speziellen Art des Messens am Messergebnis beteiligt. Messobjekte, Messinstrumente und Beobachter sind eine untrennbare Einheit.
Und weil dem so ist, können wir nie die Realität in ihrem Wesen erkennen. Wir können nicht vom Messinstrument abstrahieren. Deshalb ist das für uns Realität, was die Messinstrumente anzeigen. Eine dahinter stehende "wahre" Realität ist uns prinzipiell unzugänglich, wenn sie denn überhaupt gegeben ist. Die Quantentheorie verneint eine dahinterstehende Realität.
M.f.G. Eugen Bauhof�
tags: Realismus1gegreit Stringtheorie1gegreit Realitätsannahme1gegreit
 Nach oben
Nach oben