Relativitätstheorie: Einsteins Feldgleichung
|
|
Auch Energie ist relativ
Relativitätstheorie: Wesentliche Unterschiede zwischen SRT und ART
|
Spezielle Relativitätstheorie
Zur Relativität kosmischer Abstände
Zur Relativität von Zeit und Raum
Beitrag 0-546
2022: Die bisher genaueste Messung gravitativer Zeitdilatation
Gravitative Zeitdilatation
und die 2022 präziseste Zeitmessung menschlicher Geschichte
Auch die Stärke von Gravitationspotential hat Einfluss auf den Verlauf der Zeit: In unmittelbarer Nähe eines massereichen Körpers gehen Uhren langsamer als in gewissem Abstand davon. Physiker konnten diese Vorhersage der allgemeinen Relativitätstheorie in den vergangenen Jahrzehnten mehrfach experimentell bestätigen, indem sie Präzisionsuhren mit Flugzeugen oder Raketen auf große Geschwindigkeiten oder Höhen brachten oder ihre Experimente auf Berge oder Türme verlegten.
Nun haben Forscher vom National Institute of Standards and Technology in Boulder (Colorado) den Effekt solch gravitativen Zeitdehnung (Zeitdilatation) dem bislang präzisesten Test unterzogen. Sie haben den Gangunterschied zweier horizontal über einander angeordneter Uhren auf der Millimeterskala verglichen.

Quelle: Einstein hat recht, sogar millimetergenau, FAZ vom 28.2.2022
Diese so extrem präzise Messung vorzunehmen verwendeten die Physiker in Boulder für ihre Messungen die derzeit beste optische Atomuhr. Sie geht noch einmal um einen Faktor fünfzig genauer als eine Cäsiumuhr. Rund hunderttausend tiefgekühlte Strontiumatome werden hier mit sich kreuzenden Laserstrahlen in einer optischen Gitterstruktur in der Schwebe gehalten und mit einem extrem stabilen roten Laserstrahl angeregt. Schwingen die Atome und das externe Laserfeld im Takt, wird die Frequenz des von den Atomen ausgesandten Lichts und damit die Taktrate der Strontium-Atomuhr gemessen. Da man viele tausend synchron schlagende Taktgeber vorliegen hat, erreicht man eine deutlich größere Messgenauigkeit, als wenn man mit einem einzelnen Ion arbeiten würde.
Mögliche Anwendungen für derart genaue Messung sehen die Forscher z.B. in der Geodäsie. Die präzisen Chronometer könnten dazu genutzt werden, genaue Höhenprofile von Bergen zu erstellen oder die Tiefe der Ozeane präzise auszuloten. Sogar für die Erdbebenvorhersage ließen sich die genauen Strontium-Atomuhren einsetzen.
|
Diese neue Messung verbessert deutlich den bisherigen Rekord aus 2010, auf den in (2010) hingewiesen wird wie folgt:
"According to general relativity, atomic clocks at different elevations in a gravitational field tick at different rates. The frequency of the atoms' radiation is reduced—shifted toward the red end of the electromagnetic spectrum—when observed in stronger gravity, closer to Earth. That is, a clock ticks more slowly at lower elevations. This effect has been demonstrated repeatedly; for example, NIST physicists measured it in 2010 by comparing two independent atomic clocks, one positioned 33 centimeters (about 1 foot) above the other".
und die 2022 präziseste Zeitmessung menschlicher Geschichte
Auch die Stärke von Gravitationspotential hat Einfluss auf den Verlauf der Zeit: In unmittelbarer Nähe eines massereichen Körpers gehen Uhren langsamer als in gewissem Abstand davon. Physiker konnten diese Vorhersage der allgemeinen Relativitätstheorie in den vergangenen Jahrzehnten mehrfach experimentell bestätigen, indem sie Präzisionsuhren mit Flugzeugen oder Raketen auf große Geschwindigkeiten oder Höhen brachten oder ihre Experimente auf Berge oder Türme verlegten.
Nun haben Forscher vom National Institute of Standards and Technology in Boulder (Colorado) den Effekt solch gravitativen Zeitdehnung (Zeitdilatation) dem bislang präzisesten Test unterzogen. Sie haben den Gangunterschied zweier horizontal über einander angeordneter Uhren auf der Millimeterskala verglichen.

Quelle: Einstein hat recht, sogar millimetergenau, FAZ vom 28.2.2022
Diese so extrem präzise Messung vorzunehmen verwendeten die Physiker in Boulder für ihre Messungen die derzeit beste optische Atomuhr. Sie geht noch einmal um einen Faktor fünfzig genauer als eine Cäsiumuhr. Rund hunderttausend tiefgekühlte Strontiumatome werden hier mit sich kreuzenden Laserstrahlen in einer optischen Gitterstruktur in der Schwebe gehalten und mit einem extrem stabilen roten Laserstrahl angeregt. Schwingen die Atome und das externe Laserfeld im Takt, wird die Frequenz des von den Atomen ausgesandten Lichts und damit die Taktrate der Strontium-Atomuhr gemessen. Da man viele tausend synchron schlagende Taktgeber vorliegen hat, erreicht man eine deutlich größere Messgenauigkeit, als wenn man mit einem einzelnen Ion arbeiten würde.
Mögliche Anwendungen für derart genaue Messung sehen die Forscher z.B. in der Geodäsie. Die präzisen Chronometer könnten dazu genutzt werden, genaue Höhenprofile von Bergen zu erstellen oder die Tiefe der Ozeane präzise auszuloten. Sogar für die Erdbebenvorhersage ließen sich die genauen Strontium-Atomuhren einsetzen.
|
Diese neue Messung verbessert deutlich den bisherigen Rekord aus 2010, auf den in (2010) hingewiesen wird wie folgt:
"According to general relativity, atomic clocks at different elevations in a gravitational field tick at different rates. The frequency of the atoms' radiation is reduced—shifted toward the red end of the electromagnetic spectrum—when observed in stronger gravity, closer to Earth. That is, a clock ticks more slowly at lower elevations. This effect has been demonstrated repeatedly; for example, NIST physicists measured it in 2010 by comparing two independent atomic clocks, one positioned 33 centimeters (about 1 foot) above the other".
Beitrag 0-469
Unter welchen Umständen SRT schon ART ist
Unter welchen Bedingungen ein gegebenes Raumzeit-Szenario S
sich per SRT ebenso genau wie per ART durchrechnen lässt
Das sog. Zwillingsparadoxon ist Spezialfall eines Szenarios S, in dem sich zwei Objekte C und D auf unterschiedlichen Weltlinien durch die Raumzeit bewegen.
Die notwendige und hinreichende Bedingung dafür, dass S selbst schon mit Mitteln der SRT — quantitativ wie qualitativ — beliebig genau behandelbar ist, besteht darin, dass S per SRT modellierbar ist.
Dies lässt sich einsehen wie folgt:
Im Sinne der ART ist die Raumzeit eine differenzierbare Mannigfaltigkeit, d.h. wer darin räumlich weit verteilte Szenarien behandeln will, kann sie nur behandeln mit Hilfe von Störungsrechnung und Argumentation in den Tangentenräumen, d.h. anhand sog. » Karten «, deren jede eine offene Umgebung des Ereignisses E(T) zeigt, in dem der Tangentenraum T — ein 4-dimensionaler Vektorraum mit Minkowsi-Metrik — die Raumzeit der ART berührt.
Brauchbar ist jede dieser Karten aber nur bis hin zum Beobachtungshorizont H(E) des Ereignisses E = E(T) = Ursprung des in T genutzten Koordinatensystems.
Aber auch in der Raumzeit gibt es entsprechend große und kleine Regionen, und so komme ich zur Einsicht:
Das Szenario S ist mit Hilfe der SRT genau dann — und in diesem Fall sogar beliebig genau — durchrechenbar, wenn
Dieses Ergebnis bleibt richtig auch für den Fall, dass zwischen den Weltlinien von C einerseits und D andererseits ein oder mehrere Schwarze Löcher liegen (für deren Inneres Karten, welche beide Weltlinien ganz oder teilweise zeigen, natürlich nichts aussagen würden: Jene Karten wären dort einfach nicht definiert).
sich per SRT ebenso genau wie per ART durchrechnen lässt
Das sog. Zwillingsparadoxon ist Spezialfall eines Szenarios S, in dem sich zwei Objekte C und D auf unterschiedlichen Weltlinien durch die Raumzeit bewegen.
Die notwendige und hinreichende Bedingung dafür, dass S selbst schon mit Mitteln der SRT — quantitativ wie qualitativ — beliebig genau behandelbar ist, besteht darin, dass S per SRT modellierbar ist.
Dies lässt sich einsehen wie folgt:
Im Sinne der ART ist die Raumzeit eine differenzierbare Mannigfaltigkeit, d.h. wer darin räumlich weit verteilte Szenarien behandeln will, kann sie nur behandeln mit Hilfe von Störungsrechnung und Argumentation in den Tangentenräumen, d.h. anhand sog. » Karten «, deren jede eine offene Umgebung des Ereignisses E(T) zeigt, in dem der Tangentenraum T — ein 4-dimensionaler Vektorraum mit Minkowsi-Metrik — die Raumzeit der ART berührt.
Brauchbar ist jede dieser Karten aber nur bis hin zum Beobachtungshorizont H(E) des Ereignisses E = E(T) = Ursprung des in T genutzten Koordinatensystems.
Man kann sich das gut vorstellen, indem man sich ein Wasserfahrzeug W vorstellt, mit dessen Hilfe eine Persion P über den Atlantik von z.B. Amsterdam nach z.B. New York reist:
Über weite Strecken der Reise hinweg wird — der Krümmung der Erdoberfläche wegen — keine Küste sichtbar sein, gegen Ende der Reise aber wird sich das ändern: Der Beobachtungshorizont H(P) von P verschiebt sich mit W, so dass die Karten, die man an Bord von W nutzt — sie entsprechen den eben erwähnten "Karten" im Sinne der Differentialgeometrie — ständig ausgetauscht werden müssen.
Nun gibt es aber auch kleine Gewässer, wie etwa den Chiemsee, den zu überqueren man die zu Beginn der Reise gewählte Karte nie auszutauschen braucht, da jeder Weg, den das Schiff W dort nehmen kann, deutlich kürzer ist als der Radius des Beobachtungshorizonts der Ablegestelle.
Aber auch in der Raumzeit gibt es entsprechend große und kleine Regionen, und so komme ich zur Einsicht:
Das Szenario S ist mit Hilfe der SRT genau dann — und in diesem Fall sogar beliebig genau — durchrechenbar, wenn
- eine Raumzeit-Karte K existiert, welche komplett die beiden Weltlinien von C und D zeigt
- und wenn ferner die Weltlinien von C und D durch kein nennenswertes Gravitationsfeld führen.
Dieses Ergebnis bleibt richtig auch für den Fall, dass zwischen den Weltlinien von C einerseits und D andererseits ein oder mehrere Schwarze Löcher liegen (für deren Inneres Karten, welche beide Weltlinien ganz oder teilweise zeigen, natürlich nichts aussagen würden: Jene Karten wären dort einfach nicht definiert).
Beitrag 0-343
Warum Einstein — aber nicht Newton — Gravitationswellen vorhersagen konnte
Warum Einstein (aber nicht Newton) Gravitationswellen vorhersagen konnte
Der Grund hierfür:
Warum das zur Folge hat, dass es Gravitationswellen geben muss, erklärt sehr schön Claus Kiefer auf Seite 64 seines Buches Der Quantenkosmos:
Quelle: Claus Kiefer: Der Quantenkosmos, Fischer 2008, S. 64.
Seit September 2015 wurden bis Ende 2017 schon insgesamt 5 Gravitationswellen nachgewiesen. Eine kam aus einem Ereignis, das 3 Mrd. Lichtjahre von uns entfernt stattfand.
Der Grund hierfür:
- Nach Newton wirkt die Gravitationskraft instantan über beliebige Entfernungen hinweg.
- Nach Einstein aber kann auch Gravitationswirkung sich höchstens mit Lichtgeschwindigkeit ausbreiten.
Warum das zur Folge hat, dass es Gravitationswellen geben muss, erklärt sehr schön Claus Kiefer auf Seite 64 seines Buches Der Quantenkosmos:
Claus Kiefer:
Betrachten wir zwei Körper — A und B —, die sich wegen gravitativer Anziehung aufeinander zu bewegen. Nehmen wir an (jetzt nur als Gedankenexperiment), dass diese Körper, wenn sie aufeinander prallen, durch einen Mechanismus mit Stahlfedern wieder abgestoßen werden und sich zurückbewegen, bevor sie sich erneut annähern.
Bei der Bewegung nach außen spürt A den Zug von B in einer Stärke, wie sie bestand, als sie sich noch etwas näher waren — schließlich braucht die Gravitationswirkung ja eine endliche Zeit, um von B nach A zu gelangen. Die ziehende Kraft von B ist demnach stärker, als sie es bei instantan eintretender Wirkung wäre.
Umgekehrt süprt auf dem Weg nach innen A die Kraft von B wie sie bestand, als sie noch weiter voneinander entfernt waren — schwächer also, als das bei instantaner Wirkung der Fall wäre.
Deshalb wird auf dem Weg nach außen mehr Arbeit geleistet als auf dem Weg nach innen wieder zurückgewonnen wird. Da die Gesamtenergie erhalten bleibt, muss ein Teil der Energie den lokalen Bereich der Massen verlassen haben: als Gravitationswelle.
Seit September 2015 wurden bis Ende 2017 schon insgesamt 5 Gravitationswellen nachgewiesen. Eine kam aus einem Ereignis, das 3 Mrd. Lichtjahre von uns entfernt stattfand.
Beitrag 0-20
Wo die ART allzu ungenau wird
Wo die ART zu ungenaue Aussagen macht
Einsteins Allgemeine Relativitätstheorie (ART) ist eine Theorie, die davon ausgeht, dass alle Kräfte, die wirken — und so zur Krümmung des Raumes beitragen —, sich exakt so verhalten, wie die Gravitationskraft.
Somit kann die ART natürlich auch nur dort brauchbar sein, wo die Gravitationskraft die vorherrschende Kraft ist.
Da sie nun aber die schwächste aller Grundkräfte ist, wird das sicherlich nicht dort der Fall sein, wo aufgrund kurzer oder sehr kurze Abstände kaum Masse vorhanden sein kann: dort also, wo z.B. die starke Kernkraft den überwiegenden Anteil am Kraftpotential ausmacht — allgemeiner: wo die Summe aller wirkenden Kräfte fast ausschließlich durch Kräfte zustandekommt, die auf dort vorhandene Objekte völlig a n d e r s als die Gravitationskraft einwirken.
Objekte in diesem Sinne sind E n e r g i e t r ä g e r (also keineswegs nur aus Masse bestehende Objekte).
Was bislang fehlt, ist eine Gleichung, die das Wirken aller 4 Grundkräfte auf Energieportionen welcher Art auch immer gleichermaßen gut beschreibt.
Gutes Beispiel einer Kraft, die anders wirkt als die Gravitationskraft, ist die elektromagnetische Kraft:
Sie nämlich wirkt nur auf Objekte, die Ladung tragen.
Einsteins Allgemeine Relativitätstheorie (ART) ist eine Theorie, die davon ausgeht, dass alle Kräfte, die wirken — und so zur Krümmung des Raumes beitragen —, sich exakt so verhalten, wie die Gravitationskraft.
Da sie nun aber die schwächste aller Grundkräfte ist, wird das sicherlich nicht dort der Fall sein, wo aufgrund kurzer oder sehr kurze Abstände kaum Masse vorhanden sein kann: dort also, wo z.B. die starke Kernkraft den überwiegenden Anteil am Kraftpotential ausmacht — allgemeiner: wo die Summe aller wirkenden Kräfte fast ausschließlich durch Kräfte zustandekommt, die auf dort vorhandene Objekte völlig a n d e r s als die Gravitationskraft einwirken.
Objekte in diesem Sinne sind E n e r g i e t r ä g e r (also keineswegs nur aus Masse bestehende Objekte).
Was bislang fehlt, ist eine Gleichung, die das Wirken aller 4 Grundkräfte auf Energieportionen welcher Art auch immer gleichermaßen gut beschreibt.
Sie nämlich wirkt nur auf Objekte, die Ladung tragen.
Beitrag 0-115
Wie Einsteins Feldgleichung zu lesen ist
Was die Feldgleichung der Allgemeinen Relativitätstheorie uns sagt
Die Minkoski-Metrik der ART ist gegeben durch die Gleichung
s2 = gtt (ct)2 – gtx t x – gxx x2
Da nun aber stets gtt ≤ 1 ≤ gxx ist und die Gleichheitszeichen nur im gravitationsfreien Raum gelten, erkennt man:
Die Größe gtt sagt uns, wie die lokale Krümmung der Raumzeit den Lauf einer Uhr verlangsamt,
gxx aber legt fest, wie die lokale Krümmung der Raumzeit räumliche Abstände streckt.
Genauer: Die Größe t entspricht Zeitintervallen, wie eine im gravitationsfreien Raum befindliche Uhr sie misst,
τ = gtt1/2 t aber nennt die Eigenzeit auch beschleunigter Uhren.
Bezeichnen wir die Stärke der Raumkrümmung mit R und die Energie (bzw. Masse) mit E, so haben Einsteins Gleichungen die einfache Form
R = κ E
Hier ist κ = 8πG/c4 die sog. Einsteinsche Gravitationskonstante (proportional zur Newtonschen Gravitationskonstanten G).
Würden wir in einer Welt leben, in der G = 0 ist, gäbe es keinerlei Krümmung des Raumes.
In einer Welt, in der die Lichtgeschwindigkeit größer ist als in unserem Universum, würde die Raumkrümmung deutlich schwächer ausfallen als bei uns.
Quelle: Dieter Lüst: Quantenfische, DTV 2014, S. 174-176
Die Minkoski-Metrik der ART ist gegeben durch die Gleichung
Da nun aber stets gtt ≤ 1 ≤ gxx ist und die Gleichheitszeichen nur im gravitationsfreien Raum gelten, erkennt man:
gxx aber legt fest, wie die lokale Krümmung der Raumzeit räumliche Abstände streckt.
Genauer: Die Größe t entspricht Zeitintervallen, wie eine im gravitationsfreien Raum befindliche Uhr sie misst,
τ = gtt1/2 t aber nennt die Eigenzeit auch beschleunigter Uhren.
Bezeichnen wir die Stärke der Raumkrümmung mit R und die Energie (bzw. Masse) mit E, so haben Einsteins Gleichungen die einfache Form
Hier ist κ = 8πG/c4 die sog. Einsteinsche Gravitationskonstante (proportional zur Newtonschen Gravitationskonstanten G).
Würden wir in einer Welt leben, in der G = 0 ist, gäbe es keinerlei Krümmung des Raumes.
In einer Welt, in der die Lichtgeschwindigkeit größer ist als in unserem Universum, würde die Raumkrümmung deutlich schwächer ausfallen als bei uns.
Quelle: Dieter Lüst: Quantenfische, DTV 2014, S. 174-176
Beitrag 0-453
Wie extrem genau Uhren die Relativität der Zeit bestätigen
Wie extrem genaue Atomuhren
die durch SRT und ART vorausgesagte Zeitdilatation bestätigen
In einem der Bücher des theoretischen Physikers Jörg Resag liest man:
Quelle: Jörg Resag: Die Entdeckung des Unteilbaren, Kap 7
die durch SRT und ART vorausgesagte Zeitdilatation bestätigen
In einem der Bücher des theoretischen Physikers Jörg Resag liest man:
Jörg Resag (2012):
Eine sich bewegende Uhr läuft für einen ruhenden Beobachter langsamer als eine ruhende Uhr (spezielle Relativitätstheorie). Ebenso laufen ruhende Uhren in einem statischen Gravitationsfeld umso langsamer, je weiter unten sie sich befinden (allgemeine Relativitätstheorie).
Mittlerweile gibt es Uhren, die so präzise sind, dass sich diese Effekte auch bei alltäglichen Geschwindigkeiten und Gravitationsfeldern messen lassen.
So haben James Chin-Wen Chou, Dave Wineland und Kollegen am National Institute of Standards and Technology (NIST) in Boulder (Colorado) Uhren verwendet, die auf nur einem einzigen Aluminium-Ion in einer sogenannten Paul-Falle basieren und die in 3,7 Milliarden Jahren nur eine Sekunde falsch gehen.Einfach unglaublich, dass man heute schon Materie derart präzise kontrollieren und manipulieren kann!
Das Aluminium-Ion wird dabei in einem elektromagnetischen Feld festgehalten und mit Lasern gekühlt. Ein anderer Laser feuert nun auf das Ion,
wobei seine Frequenz sehr präzise auf eine Absorptionsfrequenz des Ions abgestimmt wird. Diese Frequenz ist nun der Taktgeber der Uhr. Bei dieser Frequenzabstimmung spielt ein weiteres Ion (ein Magnesium- oder Beryllium-Ion) eine Rolle, dessen Quantenzustand mit dem des Aluminium-Ions verschränkt ist (ähnlich wie die beiden Spin-1/2-Teilchen im Einstein-Podolsky-Rosen-Experiment miteinander verschränkt sind, siehe Kapitel 2.8).
Lässt man nun das Ion bei einer Durchschnittsgeschwindigkeit von nur 10 m/s (= 35 km/h) hin- und heroszillieren, so beobachtet man eine Verlangsamung der darauf basierenden Uhr um etwa den Faktor 10-16.
Auch bei anderen Geschwindigkeiten entspricht die Zeitdilatation genau dem Wert, wie ihn die spezielle Relativitätstheorie vorhersagt.
Ebenso gelingt es, den Zeitunterschied zweier solcher Uhren im Gravitationsfeld der Erde nachzuweisen, die nur etwa 17 cm Höhenunterschied aufweisen. Die untere Uhr läuft dabei um etwa den Faktor 4 × 10-17 langsamer als die obere — das entspricht grob einer zehnmillionstel Sekunde in 80 Jahren.
Mehr dazu in: Relativity with a human touch sowie Handwerkszeug Relativität, Physik Journal 9 (2010) Nr. 11, S. 16.
Beitrag 0-280
Über die Singularitäten der Raumzeit der Allgemeinen Relativitätstheorie
Zu den Singularitäten der Lösungen der ART
Lösungen von Einsteins Feldgleichung der Allgemeinen Relativitätstheorie zu finden, ist i.A. schwierig. Zu lösen ist stets ein Anfangswertproblem.
Um überhaupt eine Lösung finden zu können, geht man meist von Anfangswertproblemen aus, die sich auf recht symmetrische Ausgangssituationen beziehen.
Störend sind natürlich in der Lösung dann gefundene Singularitäten. Sie — so dachte man früher — könnten sich vor allem wegen einer allzu hohen Symmetrie der Ausgangssituation ergeben.
In den Jahren 1965 bis 1970 aber konnten Steven Hawking, Roger Penrose und Brendan Carter zeigen,
Quelle: Gerhard Börner:
Schöpfung ohne Schöpfer? (2006), S. 91
Lösungen von Einsteins Feldgleichung der Allgemeinen Relativitätstheorie zu finden, ist i.A. schwierig. Zu lösen ist stets ein Anfangswertproblem.
Um überhaupt eine Lösung finden zu können, geht man meist von Anfangswertproblemen aus, die sich auf recht symmetrische Ausgangssituationen beziehen.
Störend sind natürlich in der Lösung dann gefundene Singularitäten. Sie — so dachte man früher — könnten sich vor allem wegen einer allzu hohen Symmetrie der Ausgangssituation ergeben.
In den Jahren 1965 bis 1970 aber konnten Steven Hawking, Roger Penrose und Brendan Carter zeigen,
- dass Singularitäten der Raumzeit der ART auch im allgemeinen, nicht-symmetrischen Fall auftreten
- und sich i.W. als stabil gegenüber kleinen Störungen erweisen.
Beitrag 2053-67
Beschleunigung und Raumkrümmung sind dasselbe !!!
Hallo Hans-m,
aus meiner Sicht habt ihr beide recht. Ihr argumentiert lediglich in unterschiedlichen Bezugssystemen:
In Wikipedia liest man:
Mit anderen Worten: Beschleunigung ist eine Art Illusion, die uns in die Wirklichkeit zurückholt, wo wir nichts von Raumkrümmung wissen (bzw. wissen wollen).
Neutraler ausgedrückt: Beschleunigung und Raumkrümmung sind unterschiedliche gedankliche Präsentationen ein und desselben Konzepts der Natur.
Gruß, grtgrt
Hans-m in 2053-65:
Okotombrok in 2053-54:
Die Erde befindet sich im käftefreien Zustand. Man kann sagen, sie fällt um die Sonne herum und der freie Fall ist keine Beschleunigung.
Die Erde bewegt sich nicht im Kreis sondern auf einer Geodäte und das ist niemals eine Beschleunigung.
Das hatten wir doch schon alles!?
Sorry, wenn ich hier widerspreche
Die Erde befindet sich in permanenter Beschleunigung
Auf die Erde wirkt eine Anziehungskraft, von ca 3,572*1022 N, die von der Sonne ausgeht.
Hallo Hans-m,
aus meiner Sicht habt ihr beide recht. Ihr argumentiert lediglich in unterschiedlichen Bezugssystemen:
- Deine Argumentation ist richtig, wenn als Bezugssystem ein 3-dimensionales kartesisches Koordinatensystem zugrundegelegt wird (der Raum also keinerlei Krümmung hat).
- Okotombrok aber argumentiert im gekrümmten Raum der ART. Zu dem ist Einstein aber gerade dadurch gelangt, dass er Beschleunigung als Raumkrümmung interpretiert hat.
In Wikipedia liest man:
Zitat:
Die ART geht davon aus, dass ein Körper, auf den keine weiteren Kräfte wirken, sich in der gekrümmten Raumzeit auf einer Geodätischen Linie bewegt.
In einer nicht gekrümmten Raumzeit würde dies der Trägheitsbewegung eines freien Körpers entsprechen, d. h. geradlinig und mit konstanter Geschwindigkeit.
Aufgrund der Krümmung der Raumzeit erscheint [uns� diese Bewegung aber räumlich gekrümmt und beschleunigt.
Mit anderen Worten: Beschleunigung ist eine Art Illusion, die uns in die Wirklichkeit zurückholt, wo wir nichts von Raumkrümmung wissen (bzw. wissen wollen).
Neutraler ausgedrückt: Beschleunigung und Raumkrümmung sind unterschiedliche gedankliche Präsentationen ein und desselben Konzepts der Natur.
Gruß, grtgrt
Beitrag 0-40
Korrektes Argumentieren mit Einsteins (starkem) Äquivalenzprinzip
Uhren, Maßstäbe und Bewegung im Gravitationsfeld
In der Allgemeinen Relativitätstheorie ist von besonderer Bedeutung Einsteins Äquivalenzprinzip, demzufolge eine Gravitationsfeld lokal einem geeignet gewählten beschleunigten Bezugssystem gleichwertig ist. Ein solches zu finden ist stets möglich. Mit anderen Worten: Wirkungen eines Gravitationsfeldes können durch Analyse des Sachverhalts im lokal äquivalenten beschleunigten Bezugssystem im feldfreien Raum ermittelt werden (nicht ganz genau, aber doch beliebig genau, wenn man nur die Situation entsprechend lokal betrachtet).
Zwei Beispiele verdeutlichen das:
Maßstabslänge im Gravitationsfeld
Beim Ausmessen der Länge zeitlicher und räumlicher Abstände kann nicht unberücksichtigt bleiben, in welchem Bezugssystem der Beobachter sitzt:
Einsteins Einschluss der Gravitation in die Struktur der Raumzeit zeigt, dass er ihren Einfluss nicht als korrekturbedürftig betrachten wollte.
Auf Seite 147-148 seine Buches Raum-Zeit erklärt Martin Carrier weiter:
In der Allgemeinen Relativitätstheorie ist von besonderer Bedeutung Einsteins Äquivalenzprinzip, demzufolge eine Gravitationsfeld lokal einem geeignet gewählten beschleunigten Bezugssystem gleichwertig ist. Ein solches zu finden ist stets möglich. Mit anderen Worten: Wirkungen eines Gravitationsfeldes können durch Analyse des Sachverhalts im lokal äquivalenten beschleunigten Bezugssystem im feldfreien Raum ermittelt werden (nicht ganz genau, aber doch beliebig genau, wenn man nur die Situation entsprechend lokal betrachtet).
Zwei Beispiele verdeutlichen das:
Martin Carrier (S. 144-145)
- Man betrachte etwa einen Lichtstrahl, der seitlich in einen beschleunigten Kasten einfällt und diesen durchquert. Im beschleunigten Bezugssystem des Kastens durchläuft der Lichtstrahl eine gekrümmte, gegen den Boden des Kastens gerichtete Bahn. Nach dem Äquivalenzprinzip ergibt sich die gleiche Bahn aber auch im Gravitationsfeld, so dass Licht im Gravitationsfeld in Richtung des Bereiches höherer Feldstärke abgelenkt wird.
- Eine ähnliche Überlegung zeigt, dass ein Gravitationsfeld den Gang von Uhren verlangsamt: Vom hinteren Ende eines beschleunigten Kastens werde Licht ausgesandt. Wenn es das vordere Ende des Kastens erreicht, bewegt sich dieser schon mit etwas größerer Geschwindigkeit. Bei deiner Relativbewegung zwischen Sender und Empfänger tritt aber stets eine Doppler-Verschiebung auf. Hier im Beispiel ist das eine Rot-Verschiebung, da der Empfänger sich vom der Lichtquelle entfernt.
Bei Rückübertragung auf das Gravitationsfeld bedeutet das, dass eine gegen die Richtung der Schwerebeschleunigung (also gleichsam aufwärts) bewegter Lichtstrahl ebenfalls eine Rotversschiebung erfährt.
Fasst man jeden Wellenberg der Lichtwelle als Zeitsignal auf, so werden — wegen dieser Dopplerabsenkung der Frequenz — bei einem Betrachter am vorderen Ende des Kastens die Wellenberge mit vergrößertem Zeitabstand ankommen. Wenn also eine Uhr am hinteren Ende des Kastens Zeitsignale aussendet, so haben diese beim Empfang am vorderen Ende einen größeren Zeitabstand als die einer am vorderen Ende montierten baugleichen Uhr. Aus Sicht eines am vorderen Ende platzierten Beobachters geht deswegen die Uhr am hinteren Ende langsamer als seine eigene.
In der Rückübertragung bedeutet dies, dass jede Uhr im stärkeren Gravitationsfeld gegenüber einer gleich gebauten im schwächeren Gravitationsfeld zurückbleibt.
Martin Carrier (S. 145-146)
Um das Verhalten von Maßstäben im Gravitationsfeld zu ermitteln geht man wieder in das lokal äquivalente beschleunigte Bezugssystem, etwa eine rotierende Scheibe: Vom Standpunkt eines nicht mitrotierenden Beobachters aus erfahren Maßstäbe entlang der Peripherie eine Lorentz-Kontraktion, während dies bei radial orientierten Maßstäben nicht der Fall ist.
Konsequenz daraus: Das von Umfang und Durchmesser eines Kreises auf der Scheibe gemessene Verhältnis wird nicht mehr π sein, was eine Abweichung von euklidischer Geometrie anzeigt.
Diesem Befund kann auf zweierlei Weise Rechnung getragen werden:
- Man kann die tangential ausgerichteten Maßstäbe als kontrahiert betrachten, ihre Länge durch die Lorentz-Transformation korrigiert und so dem Raum Euklidische Geometrie geben.
- Nimmt man aber an, dass alle Maßstäbe ihre Länge unabhängig von ihrer Orientierung beibehalten, so ist keine Korrektur erforderlich, aber das gemessene Verhältnis von Umfang und Durchmesser muss dann als Anzeichen für das Vorliegen einer nicht-Euklidischen Geometrie gedeutet werden.
Die Verallgemeinerung dieser Behandlung führt auf folgenden Schluss:
Wenn man die Invarianz von Maßstäben bei Transport voraussetzt,
ergibt sich in beschleunigten Bezugssystemen eine nicht-Euklidische Geometrie.
Voraussetzung aber ist, dass man auf die Korrektur der erhaltenen Längenverhältnisse verzichtet.
Dieser Verzicht macht Sinn, denn die Gravitation ist eine nicht vom Material der Maßstäbe abhängige universelle Kraft. Der Verzicht auf Korrektur läuft darauf hinaus, ihren Einfluss nicht als Störung (Verzerrung) der Maßstäbe zu betrachten.
Auf Seite 147-148 seine Buches Raum-Zeit erklärt Martin Carrier weiter:
- Sie beinhalten die lokale Energie- und Impulserhaltung sowie die Bewegungsgleichung (in Newtons Theorie müssen das Gravitationsgesetz
und die Gleichung zur Beschreibung von Bewegungen im Gravitationsfeld separat angegeben werden).
- Sie haben zur Folge, dass "Testteilchen" (hypothetische Masseteilchen, die weder rotieren noch Ausdehnung haben) im Gravitationsfeld zeitartigen Geodäten folgen.
- Ebenso ergeben sich aus den Feldgleichungen alle auf der Grundlage des Äquivalenzprinzips ableitbaren Effekte wie Ablenkung von Lichtstrahlen oder die Verlangsamung des Uhrengangs im Gravitationsfeld.
Einsteins Geometrisierung der Gravitation hat auch zur Folge, dass weder Raum noch Zeit ein festgefügtes Behältnis für die wechselnden Ereignisse unserer Erscheinungs- welt bilden, sondern — wie die Gravitation — dem Einfluß von Energie, speziell Materie, unterworfen sind:
In Abhängigkeit von der Verteilung von Massen und Feldern ändert sich die Raumzeitmetrik und die Geodätenstruktur (als Geodäte bezeichnet man jeden Weg durch die Raumzeit, der zwischen je zwei auf ihm liegenden Ereignissen den kürzesten Weg darstellt).
Dieser Einfluss von Energieverteilung auf die Struktur der Raumzeit wird durch Einsteins Feldgleichungen der Gravitation beschrieben. Sie machen die Verteilung von Materie und Energie zudem noch zur Q u e l l e des Gravitationsfeldes: Sie verknüpfen den sog. Energie-Impuls-Tensor, der alle Quellen des Gravitationsfeldes mit Ausnahme des Gravitationsfeldes selbst enthält, mit Metrik und Krümmung der Raumzeit.
Die Feldgleichungen sind Einsteins Gegenstück zu Newtons Gravitationsgesetz. Physikalisch neu ist, dass das Gravitationsfeld so zu seiner eigenen Quelle wird.
Im Gegensatz zur Newtonschen Gravitationskraft ist Einsteins geometrisierte Gravitationskraft selbst schwer. Diese Eigentümlichkeit führt zur Nicht-Linearität der Feldgleichungen und findet ihren empirischen Ausdruck u.A. in sog. Gravitationswellen und dem im Vergleich zur Newtonschen Theorie schnelleren Voranschreitens des Merkurperihels.
Durch die Gravitation entsteht in der ART eine Abweichung von der sog. Minkowski-Raumzeit der SRT: In jener werden — da der Minkowski-Raum flach ist — Abstände über die Minkowski-Metrik quantifiziert, wohingegen in der Raumzeit der ART örtlich und zeitlich variable, kompliziertere Metriken anzwenden sind.
Einsteins Feldgleichungen übertreffen ihr Newtonsches Gegenstück beträchtlich an logischer Kraft.
Beitrag 0-41
Die durch Thirring und Deser vorgeschlagene Normierung unserer Raumzeit-Realität
Die Thirring-Deser-Normierung der ART
Wie in Beitrag 0-40 erklärt, hat Einstein seine Formulierung der ART so gewählt, dass Längeneinheiten für alle Beobachter gleich definiert sind (was dann zu nicht-Euklidischer Geometrie des Raumes führt). Diese Konvention aber ist keineswegs zwingend.
Und tatsächlich: Es gibt eine von Walter Thirring in den 1950er Jahren erarbeitete und etwa 20 Jahre später von Stanley Deser wesentlich verbesserte Fassung der Einsteinschen Feldgleichungen,
die mit dem Anspruch verbunden ist, dass die Raumzeit Euklidische Geometrie habe (mit überall gleicher Metrik).
Man sieht sich hier einmal mehr an Niels Bohr erinnert, der betont hat:
Die Physik kann nicht ergründen, wie die Natur funktioniert [ Wirklichkeit ].
Sie kann nur darüber sprechen, wie sie sich dem Beobachter darstellt [ Realität ].
Die unterschiedliche Formalisierung der ART durch Einstein einerseits und Thirring/Deser andererseits zeigt zudem, dass, was wir als Realität betrachten, zudem noch von durch uns selbst gewählten K o n v e n t i o n e n abhängig sein kann.
Bemerkenswert an der durch Thirring/Deser gefundene Normierung der Raumzeit ist vor allem, dass sie die Sonderstellung der Gravitation — die ihr durch Einsteins Geometrisierung zuwuchs — aufhebt.
Sie aufzuheben könnte notwendig sein, um zu einer Theorie zu kommen, die ART und Quantenmechanik zusammenführt: Diese künftige Theorie (Quantengravitation), die zu entwickeln nun schon ein halbes Jahrhundert auf der wissenschaftlichen Tagesordnung steht, wird ja aller Erwartung nach die Gravitation nach dem Muster der übrigen physikalischen Wechselwirkungen behandeln müssen: als eine Kraft, die q u a n t i s i e r t ist.
Wie in Beitrag 0-40 erklärt, hat Einstein seine Formulierung der ART so gewählt, dass Längeneinheiten für alle Beobachter gleich definiert sind (was dann zu nicht-Euklidischer Geometrie des Raumes führt). Diese Konvention aber ist keineswegs zwingend.
Und tatsächlich: Es gibt eine von Walter Thirring in den 1950er Jahren erarbeitete und etwa 20 Jahre später von Stanley Deser wesentlich verbesserte Fassung der Einsteinschen Feldgleichungen,
Martin Carrier (S. 166-167 seines Buches Raumzeit, de Gruyter, 2009)
Die Thirring-Deser-Fassung der Einsteinschen Feldgleichungen stellt die Gravitation als universelles Kraftfeld in einem f l a c h e n Raum dar, der mit einer überall gleichen Minkowski-Metrik ausgestattet ist.
In Umkehrung der Einsteinschen Vorgehensweise gibt man die Raumzeit-Struktur vor und passt das Verhalten von Maßstäben und Uhren sowie die Bewegung freier [hypothetisch ausdehnungsloser Test-] Teilchen an sie an durch die Einführung universeller Kräfte.
Die Gravitation verzerrt dann die M a ß s t ä b e , beinflusst aber n i c h t die Geometrie.
Die Thirring-Deser-Fassung enthält entsprechend eine de-geometrisierte Version der Einsteinschen Feldgleichungen unter Bewahrung der Kausalität.
Beide Ansätze sind empirisch äquivalent, wenn auch nicht in jeder Hinsicht gleichwertig: In empirischer Hinsicht ergeben sich Abweichungen die Topologie des Raumes betreffend, da man mit einer flachen Hintergrundgeometrie kein geschlossenes Universum wiedergeben kann.
Damit ist die These von der Konventionalität der physikalischen Geometrie der Raumzeit — auch unter Bewahrung der kausalen Erklärbarkeit — nicht ohne Stütze. ...
Die adaptierte These belegt die generelle Ansicht von der Unterbestimmtheit von Theorien durch die Erfahrung, mit der Folge, dass Raum-Zeit-Theorien keine spezifische Form von Konventionalität enthalten.
Man sieht sich hier einmal mehr an Niels Bohr erinnert, der betont hat:
Sie kann nur darüber sprechen, wie sie sich dem Beobachter darstellt [ Realität ].
Die unterschiedliche Formalisierung der ART durch Einstein einerseits und Thirring/Deser andererseits zeigt zudem, dass, was wir als Realität betrachten, zudem noch von durch uns selbst gewählten K o n v e n t i o n e n abhängig sein kann.
Bemerkenswert an der durch Thirring/Deser gefundene Normierung der Raumzeit ist vor allem, dass sie die Sonderstellung der Gravitation — die ihr durch Einsteins Geometrisierung zuwuchs — aufhebt.
Sie aufzuheben könnte notwendig sein, um zu einer Theorie zu kommen, die ART und Quantenmechanik zusammenführt: Diese künftige Theorie (Quantengravitation), die zu entwickeln nun schon ein halbes Jahrhundert auf der wissenschaftlichen Tagesordnung steht, wird ja aller Erwartung nach die Gravitation nach dem Muster der übrigen physikalischen Wechselwirkungen behandeln müssen: als eine Kraft, die q u a n t i s i e r t ist.
Beitrag 0-43
Was Einstein zu seiner Gravitationstheorie führte (1): Das Machsche Prinzip
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als erstes
Das Machsche Prinzip
Was Einstein das Machsche Prinzip nannte, bringt zum Ausdruck, dass Einstein — wie vor ihm schon Leibniz und Mach — nicht an die Existenz eines "absoluten" Raumes glaubte, der auch als leerer Raum noch existieren würde, als Behälter also, der durch Objekte bewohnt oder auch nicht bewohnt sein könnte.
Newton — der in diesem Punkt ganz anderer Ansicht war als sein Zeitgenosse Leibniz — hatte argumentiert, dass das Auftreten von Trägheitskräften nichts mit Beziehungen zwischen den betroffenen Körpern und anderer Körper zu tun habe, sondern stattdessen die "wahre Bewegung" des Körpers, d.h seine Bewegung relativ zum absoluten Raum widerspiegle.
Obgleich das Machsche Prinzip Einsteins Weg zur ART bahnte, ist es in der voll entwickelten Theorie tatsächlich n i c h t erfüllt
( wie Carrier in den Abschnitten 4.1.4 und 4.2.2 seines Buches erklärt ):
Für jede Theorie muß grundsätzlich unterschieden werden
Es gibt demzufolge zwei unterschiedliche philosophische Haltungen:
Für eine umfassende Beschreibung kosmischer Strukturen aber reicht Friedmans Lösung n i c h t aus: Lokalen Abweichungen von der Homogenität — etwa bei Planetensystemen oder Schwarzen Löchern — muss durch Größen Rechnung getragen werden, die absolut sind, bei denen also nicht alle geometrischen Strukturen einfach nur auf die relative Lage der Körper zueinander zurückführbar sind.
Noch 1917 hat Willem de Sitter Einstein darauf aufmerksam gemacht, dass seine Feldgleichungen auch absolut leere, unendlich weite Raumzeiten zulassen (und die noch nicht mal statisch sein müssen). Wegen der hier angenommenen kosmologischen Konstanten zieht sich die Raumzeit zunächst zusammen, expandiert dann aber wieder (was aber beides erst später klar wurde). Diese Beispiele zeigen, dass die Metrik doch nicht — wie Einstein dachte — allein durch den Energie-Impuls-Tensor bestimmt ist.
Ausgehend hiervon sah Einstein schließlich auch ein, dass seine Theorie gar nicht auf der Relativität der trägen Masse aufbaut oder sie erfordert, sondern lediglich auf der Relativität der Bezugssysteme. In einem Brief aus 1954 schrieb er dann schließlich, dass man vom Mach'schen Prinzip überhaupt nicht mehr sprechen sollte.
Damit ist nun aber erneut die Frage berechtigt, ob die Natur nicht vielleicht doch auch absolut leere Raumzeit kennt.
Das Machsche Prinzip
Was Einstein das Machsche Prinzip nannte, bringt zum Ausdruck, dass Einstein — wie vor ihm schon Leibniz und Mach — nicht an die Existenz eines "absoluten" Raumes glaubte, der auch als leerer Raum noch existieren würde, als Behälter also, der durch Objekte bewohnt oder auch nicht bewohnt sein könnte.
Newton — der in diesem Punkt ganz anderer Ansicht war als sein Zeitgenosse Leibniz — hatte argumentiert, dass das Auftreten von Trägheitskräften nichts mit Beziehungen zwischen den betroffenen Körpern und anderer Körper zu tun habe, sondern stattdessen die "wahre Bewegung" des Körpers, d.h seine Bewegung relativ zum absoluten Raum widerspiegle.
Martin Carrier (in seinem Buch Raum-Zeit, de Gruyter 2009, S. 138-139)
Einstein hielt nichts von diesem Gedanken. Sein zentrales Motiv war die bei Newton angenommene Einseitigkeit der Kausalwirkung, nach der der absolute Raum Trägheitskräfte entstehen lässt ohne dass es Rückwirkung der Körper auf ihn gibt.
Einen solch einseitigen Kausaleinfluss hielt Einstein für widersinnig und wollte ihn durch die Vorstellung ersetzen, dass die Trägheitseigenschaften bewegter Körper generell durch ein physikalisches Feld bestimmt sind, ähnlich dem elektromagnetischen Feld.
In diesem Denkansatz kann der Raum zwar weiterhin physikalische Wirkung entfalten, jedoch müssen umgekehrt die Körper auch auf ihn Einfluss nehmen können. Für Einstein bedeutet das: Die metrischen und geodätischen Eigenschaften der Raumzeit sollten zur Gänze durch die relativen Lagen und Bewegungen von Körpern (oder anderen Energieformen) festgelegt sein.
Er nannte dieses Prinzip das Machsche Prinzip .
Es impliziert, dass das Auftreten von Trägheitskräften zur Gänze durch Relativbewegungen festgelegt ist, nicht aber durch Bewegungen der Körper gegen den Raum.
Obgleich das Machsche Prinzip Einsteins Weg zur ART bahnte, ist es in der voll entwickelten Theorie tatsächlich n i c h t erfüllt
( wie Carrier in den Abschnitten 4.1.4 und 4.2.2 seines Buches erklärt ):
Für jede Theorie muß grundsätzlich unterschieden werden
- zwischen der Theorie einerseits und
- den zu ihr konformen Modellen andererseits (die sich ja in durch die Theorie nicht voll bestimmten Eigenschaften durchaus unterscheiden können).
Es gibt demzufolge zwei unterschiedliche philosophische Haltungen:
- Als Relationalismus bezeichnet man einen Standpunkt, der zwar anerkennt, dass die ART Lösungen kennt, die das Machsche Prinzip nicht automatisch erfüllen, der diese Lösungen aber als
philosophisch belanglos einstuft, da sie nicht mit den Erfahrungsbedingungen unserer Welt übereinstimmen.
- Der absolute Ansatz dagegen kennt keine Konzentration auf die faktisch realisierten Lösungen. Seine Anhänger stehen auf dem Standpunkt, dass die ART keinen Rückgriff auf Bezugskörper verlange und keine Rückführung von Trägheitskräften auf Relativbewegungen erzwinge. Die nicht-Machschen Lösungen seien ebenfalls relevant, da sie zur Beschreibung kleinräumiger kosmischer Strukturen (mit ihren lokalen Abweichungen von Homogenität und Isotropie) gebraucht werden.
Für eine umfassende Beschreibung kosmischer Strukturen aber reicht Friedmans Lösung n i c h t aus: Lokalen Abweichungen von der Homogenität — etwa bei Planetensystemen oder Schwarzen Löchern — muss durch Größen Rechnung getragen werden, die absolut sind, bei denen also nicht alle geometrischen Strukturen einfach nur auf die relative Lage der Körper zueinander zurückführbar sind.
Rüdiger Vaas (in seinem Buch Jenseits von Einsteins Universum, 2016, S. 220-222):
Den Begriff das Mach'sche Prinzip hat Einstein 1918 zu Ehren des 1916 verstorbenen Ernst Mach eingeführt. Er steht für Machs Aussage, dass die Trägheit eines Körpers bestimmt sei durch den Einfluss, den alle sonst noch im All vorhandenen Körper auf ihn haben.
In Einsteins Theorie ausgedrückt:
Der durch den Metriktensor gμν beschriebene » Raumzustand «
— auch das Gravitationsfeld, welches durch den Energie-Impuls-Tensor Tμν bedingt wird —
sei r e s t l o s durch die Massen der Körper bestimmt.
Einstein bedauerte, dieses Prinzip zunächst nicht klar genug vom Relativitätsprinzip unterschieden zu haben, das er nun so definierte:
» Die Naturgesetze sind nur Aussagen über zeiträumliche Koinzidenzen.
Sie finden d e s h a l b ihren einzig natürlichen Ausdruck in allgemein kovarianten Gleichungen. «
Einstein räumte ein, das Mach'sche Prinzip würde » keineswegs von allen Fachgenossen geteilt «, er selbst aber empfinde » seine Erfüllung als unbedingt notwendig «.
Ob Einstein berechtigt war, sich auf Mach zu beziehen, erscheint fraglich (und wird von Wissenschaftsphilosophen wie etwa John Norton mit guten Gründen bezweifelt): Mach selbst hatte wohl keine klare Konzeption von dem, was Einstein nach seinem Tode das Mach'sche Prinzip nannte.
Mittlerweile gibt es mindestens 20 Formulierungen, keine deckungsgleich mit einer anderen, und manche sind ziemlich sicher falsch ...
Klaus Kiefer (auf S. 60 in Quantenkosmos):
Einstein verstand das Machsche Prinzip ursprünglich so, dass die Geometrie der Raumzeit — ihre Metrik — durch die Materieverteilung eindeutig bestimmt sein sollte. Wie Einstein selbst aber nachträglich feststellen musste, ist das in der ART nun aber doch nicht der Fall: Die Metrik geht in alle bekannten Materiegleichungen ein und kann daher nicht durch die Materie bestimmt sein.
Zudem sind es ja gerade die lokalen Gravitationsfelder, welche für das lokale Trägheitsverhalten am dominantesten bestimmen (und nicht — wie noch Mach meinte — die fernen Fixsterne bzw. alle Körper im Raum gleichermaßen).
Noch 1917 hat Willem de Sitter Einstein darauf aufmerksam gemacht, dass seine Feldgleichungen auch absolut leere, unendlich weite Raumzeiten zulassen (und die noch nicht mal statisch sein müssen). Wegen der hier angenommenen kosmologischen Konstanten zieht sich die Raumzeit zunächst zusammen, expandiert dann aber wieder (was aber beides erst später klar wurde). Diese Beispiele zeigen, dass die Metrik doch nicht — wie Einstein dachte — allein durch den Energie-Impuls-Tensor bestimmt ist.
Ausgehend hiervon sah Einstein schließlich auch ein, dass seine Theorie gar nicht auf der Relativität der trägen Masse aufbaut oder sie erfordert, sondern lediglich auf der Relativität der Bezugssysteme. In einem Brief aus 1954 schrieb er dann schließlich, dass man vom Mach'schen Prinzip überhaupt nicht mehr sprechen sollte.
Damit ist nun aber erneut die Frage berechtigt, ob die Natur nicht vielleicht doch auch absolut leere Raumzeit kennt.
Beitrag 0-44
Was Einstein zu seiner Gravitationstheorie führte (2): Das Äquivalenzprinzip
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als zweites
Das schwache und das starke Äquivalenzprinzip
Unter dem s c h w a c h e n Äquivalenprinzip versteht man die Gleichheit von schwerer und träger Masse:
Danach stellen schwere und träge Masse lediglich unterschiedliche Manifestationen einer einzigen Grundgröße dar.
Nach dem schwachen Äquivalenzprinzip lässt sich gleichförmige Beschleunigung im feldfreien Raum nicht von geradlinig-gleichförmiger Bewegung im einem gleichförmigen Gravitationsfeld unterscheiden.
Verknüpft mit Machschen Prinzip führt das starke Äquivalenzprinzip auf ein Charakteristikum der ART, welches darin besteht, den absoluten Raum zu vermeiden.
WICHTIG aber:
Bisher konnten Experimente das Äquivalenzprinzip bis zu einer Genauigkeit von 10-13 bestätigen. Dennoch ruht man nicht:
Folgen des Äquivalenzprinzips
Nach dem Äquivalenzprinzip ist es physikalisch nicht unterscheidbar, ob eine in einem System auftretende Kraft sich als Folge von Beschleunigung ergibt oder durch Gravitationsquellen hervorgerufen ist.
Mit anderen Worten: Schwerkraft und Trägheitskräfte (wie etwa die Fliehkraft) sind aufsummierbar und können sich daher — als gerichtete Kräfte — auch gegenseitig aufheben.
Die Erde umkreisende Raumfahrer etwa machen sich das zunutze: In der typischen Flughöhe von IIS und Mir ist die Schwerkraft nur etwa 15% geringer als auf der Erdoberfläche. Schwerelos sind die Raumfahrer darin nur deswegen, weil
Historische Notiz:
Für Newton war Trägheit durch den Raum hervorgerufen, Gravitation aber durch die sich anziehenden Objekte im Raum.
Erst Einstein sah beide als Erscheinungsformen ein und derselben Sache: der Geometrie der Raumzeit.
Daher ist selbst noch die Fliehkraft, der wir während einer Karusselfahrt ausgesetzt sind, ein Aspekt der Gravitation.
Das schwache und das starke Äquivalenzprinzip
Unter dem s c h w a c h e n Äquivalenprinzip versteht man die Gleichheit von schwerer und träger Masse:
Einstein (1922)
Die bisherige Mechanik hat diesen wichtigen Sachverhalt zwar registriert, aber nicht interpretiert.
Eine befriedigende Interpretation kann nur so zustandekommen, dass man einsieht: Dieselbe Qualität des Körpers äußerst sich je nach Umständen als Trägheit oder als Schwere.
Nach dem schwachen Äquivalenzprinzip lässt sich gleichförmige Beschleunigung im feldfreien Raum nicht von geradlinig-gleichförmiger Bewegung im einem gleichförmigen Gravitationsfeld unterscheiden.
Der Schluss ist, dass gleichförmige Beschleunigungen und homogene Gravitationsfelder für alle mechanischen Prozesse empirisch äquivalent sind.
Die Annahme, dass dies nicht allein für mechanische Prozesse, sondern sogar für s ä m t l i c h e physikalischen Vorgänge gelte, wird als s t a r k e s Äquivalenzprinzip bezeichnet. Erst Einstein sprach davon.
Verknüpft mit Machschen Prinzip führt das starke Äquivalenzprinzip auf ein Charakteristikum der ART, welches darin besteht, den absoluten Raum zu vermeiden.
WICHTIG aber:
-
Das Äquivalenzprinzip lässt sich nur auf h o m o g e n e Gravitationsfelder anwenden. Seine Erweiterung auf inhomogene Felder — solche mit räumlich
oder zeitlich wechselnder Feldintensität — verlangt eine bloß lokale Anwendung
auf räumlich und zeitlich benachbarte Ereignisse.
-
Gutes Beispiel eines inhomogenen Gravitationsfeldes ist das kugelsymmetrische Feld der Erde.
In ihm ist die Schwerebeschleunigung auf den Erdmittelpunkt gerichtet und weist daher an unterschiedlichen Orten in meist unterschiedliche Richtung.
Folglich ist das Schwerefeld der Erde n i c h t durch Übergang in ein einziges beschleunigtes Bezugssystem im feldfreien Raum nachzubilden.
Nur wer sich auf einen hinreichend kleinen Bereich des irdischen Schwerefeldes beschränkt, kann für ihn ein Bezugssystem derart wählen, dass
das Schwerefeld verschwindet (niemals ganz genau, wohl aber ausreichend genau unter praktischen Gesichtspunkten).
Auch die Tatsache, dass ein in einem beliebigen Gravitationsfeld frei fallender Beobachter die Existenz des Feldes grundsätzlich überhaupt nicht nachweisen könne, gilt nur in sehr kleinen Bereichen: Darüber hinaus nämlich wäre — genügend genaues Messgerät vorausgesetzt — die Auswirkungen der Raum-Zeit-Krümmung anhand sog. Gezeitenkräfte erkennbar, d.h. anhand der Deformationen, die sämtliche Körper im inhomogenen Gravitationsfeld erfahren. Wenn z.B. eine verformbare Kugel der Erde entgegen fällt, wirkt die Gravitationskraft am unteren Ende der Kugel stärker als am oberen (da sie ja der Erde schon näher ist), so dass die Kugel sich in Fallrichtung verlängert ind insgesamt elliptische Form annimmt.
Dass man diese Kraftdifferenz als Gezeitenkraft bezeichnet, liegt daran, dass die irdischen Wassermassen auf der dem Mond zugewandten Seite von ihm stärker angezogen werden als auf der ihm abgewandten Seite. Deshalb ist das Wasser an beiden Seiten relativ zum Erdzentrum in Richtung des Mondes beschleunigt, was — da der Mond die Erde umkreist — ständigen Wechsel zwischen Ebbe und Flut zur Folge hat.
Wirklich exakt also gilt das Äquivalenzprinzip nur in einer ausdehnungslosen Umgebung des Beobachters, die — da ausdehnungslos — nur den Punkt enthält, in dem der Beobachter ruht. Mit zunehmendem Abstand von ihm werden z.B. Gezeitenkräfte immer deutlicher hervortreten. Wirklich zu Null wird das Gravitationsfeld nur im Beobachter selbst: Das s t a r k e Äquivalenzprinzip hat nur l o k a l e Gültigkeit.
Bisher konnten Experimente das Äquivalenzprinzip bis zu einer Genauigkeit von 10-13 bestätigen. Dennoch ruht man nicht:
- Das Äquivalenzprinzip mit noch höherer Genauigkeit nachzuprüfen ist Aufgabe des von der ESA verantworteten Projekts
Weltraummission MICROSCOPE.
- Um die Jahreswende 2013/2014 wurde ein exotisches 3-Sterne-System entdeckt, mit dessen Hilfe sich die uneingeschränkte Gültigkeit des starken Äquivalenzprinzips mit um einige Größenordnungen höherer Genauigkeit als bisher wird nachprüfen lassen. Siehe Relativitätstheorie im Präzisionstest (Jan 2014).
Nach dem Äquivalenzprinzip ist es physikalisch nicht unterscheidbar, ob eine in einem System auftretende Kraft sich als Folge von Beschleunigung ergibt oder durch Gravitationsquellen hervorgerufen ist.
Mit anderen Worten: Schwerkraft und Trägheitskräfte (wie etwa die Fliehkraft) sind aufsummierbar und können sich daher — als gerichtete Kräfte — auch gegenseitig aufheben.
Die Erde umkreisende Raumfahrer etwa machen sich das zunutze: In der typischen Flughöhe von IIS und Mir ist die Schwerkraft nur etwa 15% geringer als auf der Erdoberfläche. Schwerelos sind die Raumfahrer darin nur deswegen, weil
- auf sie — da sie sich ja kreisförmig um die Erde bewegen — auch Fliehkraft wirkt
- und die Flughöhe ihrer Umlaufbahn so gewählt wurde, dass Fliehkraft und Schwerkraft sich zu Null aufaddieren.
- Möglich ist das nur, weil nach dem Äquivalenzprinzip beide Kräfte gleicher Natur sind.
Für Newton war Trägheit durch den Raum hervorgerufen, Gravitation aber durch die sich anziehenden Objekte im Raum.
Erst Einstein sah beide als Erscheinungsformen ein und derselben Sache: der Geometrie der Raumzeit.
Daher ist selbst noch die Fliehkraft, der wir während einer Karusselfahrt ausgesetzt sind, ein Aspekt der Gravitation.
Beitrag 0-45
Was Einstein zu seiner Gravitationstheorie führte (3): Das Prinzip allgemeiner Kovarianz
Ausgangspunkt von Einsteins Entwicklung der Allgemeinen Relativitätstheorie waren 3 Prinzipien. Hier als drittes
Das Prinzip allgemeiner Kovarianz
Einsteins Ziel war, seine Theorie so zu formulieren, dass ihre Ausdrücke in allen Bezugssystemen anwendbar sind — nicht allein in Inertialsystemen.
Zulässige Transformationen zwischen Bezugssystemen sollten nur eingeschränkt sein durch die Bedingungen
Wie bedeutsam das ist, wird klar, wenn man sich vor Augen führt, dass die Gesetze der Newtonschen Mechanik (wie auch der SRT) zunächst nur in Inertialsystemen gültig sind und an nicht-inertiale Bezugssysteme nur durch Einführung zusätzlicher Größen — Zentrifugalkräfte oder Crioliskräfte — anpassbar sind.
Solche Sonderstellung einer besonderen Klasse von Bezugssystemen wollte Einstein in der ART vermeiden:
Sein Ziel war, die Theorie so zu formulieren, dass ihre Gesetze in unveränderter Form in allen denkbaren Bezugssystemen gültig bleiben.
Allgemeine Kovarianz erreicht genau das. Zulässig sind danach nur Größen, die ein ganz bestimmtes Transformationsverhalten aufweisen.Man nennt sie kovariante Größen. Kovarianz ist ein der Differentialgeometrie entstammender, rein mathematischer Begriff. Einstein gelang es, ihm mit physikalischer Relevanz zu versehen. Einstein glaubte 1916, dass das Prinzip allgemeiner Kovarianz als Ausdruck und Konkretisierung eines "allgemeinen Relativitätsgesetzes" gelten könne, demzufolge sämtliche Bewegungsformen physikalisch gleichwertig sind:
Die Formulierung eines physikalischen Gesetzes heißt k o v a r i a n t , wenn sie koordinatensystem-unabhängig ist.
Das Prinzip allgemeiner Kovarianz
Einsteins Ziel war, seine Theorie so zu formulieren, dass ihre Ausdrücke in allen Bezugssystemen anwendbar sind — nicht allein in Inertialsystemen.
Zulässige Transformationen zwischen Bezugssystemen sollten nur eingeschränkt sein durch die Bedingungen
- umkehrbar eindeutig,
- stetig,
- und auch differenzierbar.
Wie bedeutsam das ist, wird klar, wenn man sich vor Augen führt, dass die Gesetze der Newtonschen Mechanik (wie auch der SRT) zunächst nur in Inertialsystemen gültig sind und an nicht-inertiale Bezugssysteme nur durch Einführung zusätzlicher Größen — Zentrifugalkräfte oder Crioliskräfte — anpassbar sind.
Solche Sonderstellung einer besonderen Klasse von Bezugssystemen wollte Einstein in der ART vermeiden:
Sein Ziel war, die Theorie so zu formulieren, dass ihre Gesetze in unveränderter Form in allen denkbaren Bezugssystemen gültig bleiben.
Allgemeine Kovarianz erreicht genau das. Zulässig sind danach nur Größen, die ein ganz bestimmtes Transformationsverhalten aufweisen.Man nennt sie kovariante Größen. Kovarianz ist ein der Differentialgeometrie entstammender, rein mathematischer Begriff. Einstein gelang es, ihm mit physikalischer Relevanz zu versehen. Einstein glaubte 1916, dass das Prinzip allgemeiner Kovarianz als Ausdruck und Konkretisierung eines "allgemeinen Relativitätsgesetzes" gelten könne, demzufolge sämtliche Bewegungsformen physikalisch gleichwertig sind:
Einstein (1922)
Wir werden dem Relativitätsprinzip im weitesten Sinne dadurch gerecht, dass wir den Gesetzen eine solche Form geben, daß sie bezüglich jedes derartigen (4-dimensionalen) Koordinatensystems gelten, d.h. daß die sie ausdrückenden Gleichungen bezüglich beliebiger Transformation kovariant sind.
Martin Carrier (in seinem Buch Raum-Zeit, de Gruyter 2009, S. 143-144)
Allerdings hat das Prinzip allgemeiner Kovarianz nichts mit der Relativität der Bewegung zu tun. Wie Erich Kretschmann 1917 zeigen konnte, beinhaltet die mathematische Tatsache der unveränderten Form der Gleichungen in beliebigen Koordinatensystemen keineswegs auch die physikalische Äquivalenz aller Bezugssysteme.Allgemeine Kovarianz bingt zum Ausdruck, dass sich die Größen der Theorie und ihre Beziehungen untereinander in koordinaten-unabhängiger Form darstellen lassen, schließt aber n i c h t aus, dass bei der Umsetzung der übergreifenden Darstellung in konkrete Bezugssysteme doch wieder spezifische Merkmale besonderer Bewegungsformen in Erscheinung treten.
Um es nochmals zu sagen:
Tatsächlich lässt sich beinahe jede Bewegungstheorie allgemein kovariant formulieren (SRT und Newtonsche Mechanik auf jeden Fall).
Dabei konkretisiert sich dann die die einheitliche Formulierung in verschiedenen Bezugssystemen auf unterschiedliche Weise.
Insbesondere treten in Nicht-Inertialsystemen unverändert Trägheitskräfte in Erscheinung, so dass sich an der Sonderstellung der Initialsysteme nichts geändert hat.Allgemeine Kovarianz ist eine mathematische Eigenschaft der F o r m u l i e r u n g einer Theorie.
Physikalische Äquivalenz von Bezugssystemen aber garantiert sie keineswegs.Neu in der ART ist allein, dass ein allgemein kovariante Formulierung dort unvermeidlich ist, da die von Punkt zu Punkt unterschiedliche Krümmung der Raumzeit keine globalen Inertialsysteme mehr zulässt (Friedmann 1983, 54-56, 207-209, 212-213).
Quelle:
- Friedmann, Michael (1983): Foundations of Space-Time Theories, Relativistic Physics and Philosphy of Science, Princeton University Press
Beitrag 0-48
Warum das Standardmodell der Elementarteilchen und Einsteins Gravitationstheorie einander widersprechen
Zum Konflikt zwischen ART und Quantentheorie
Beide Theorien unterscheiden sich grundlegend schon von ihrem begrifflichen Ansatz her:
Quellen:
Beide Theorien unterscheiden sich grundlegend schon von ihrem begrifflichen Ansatz her:
- In der Quantentheorie — und dem Standardmodell der Elementarteilchenphysik — werden physikalische Wechselwirkungen durch quantisierte Felder beschrieben,
so dass sich dort jede Wirkung von Kraft darstellt als Austausch von Überträgerteilchen (Bosonen):
- Photonen vermitteln die elektromagnetische Kraft,
- Eichbosonen die schwache Wechselwirkung
- und insgesamt 8 Gluonen die starke Kernkraft (die vor allem zwischen Quarks wirkt).
- Dass auch gravitative Wechselwirkung quantisiert sei — hypothetisch durch sog. Gravitonen (Gravitationswellen) — ist bislang nur Vermutung.
- Ganz anders Einsteins Gravitationstheorie:
Sie geht davon aus, dass Gravitationskräfte Ausdruck der Krümmung des Raumes (d.h. der Raumzeit) sind. Da die sich stetig ändert, kann Gravitation — der ART entsprechend — nicht quantisiert sein.
Martin Carrier (S. 224 in seinem Buch Raum-Zeit, de Gruyter 2009) kommt zum Schluss:
Eine der beiden Denkschulen wird weichen müssen. Vieles spricht dafür, dass es die Geometrisierung der Gravitation ist, die aufzugeben sein wird.
Nach früh gescheiterten Versuchen, auch Materie und (Energie-) Felder als besondere Raum-Zeit-Strukturen zu verstehen (Esfeld 2002, 42-43), zielen heute sämtliche Ansätze einer einheitlichen Theorie aller physikalischen Wechselwirkungen auf eine Quantentheorie der Gravitation. Bislang ist unklar, wie eine solche Theorie aussehen könnte. Dennoch ist damit zu rechnen, dass die Frage nach der Natur von Raum und Zeit vor dem Hintergrund einer künftigen Quantentheorie der Gravitation anders zu beantworten sein wird als heute.
Quellen:
- Esfeld, Michael (2002): Einführung in die Naturphilosophie, Darmstadt, Wissenschaftliche Buchgesellschaft (erschien 2011 in gründlicher Neubearbeitung)
Beitrag 0-46
Wie sich Newton einerseits und Leibniz andererseits Raum und Zeit vorgestellt hatten
Wie Newton und sein Widerpart Leibniz Raum und Zeit sahen
Newton sah den Raum als einen Behälter, in dem Objekte wohnen, die sich zeitabhängig verschieden schnell durch ihn bewegen.
Völlig anders Leibniz: Für ihn gab es diesen Behälter nicht. Er hielt den Raum ebenso wie die Zeit für etwas rein Relationales:
Die Ursprünge solch einer relationalen Theorie von Raum und Zeit gehen auf Decartes (1596-1650) zurück. In seinen Prinzipien der Philosophie vertrat er die Ansicht, dass Ausdehnung das kennzeichnende Merkmal von Materie und Raum gleichermaßen bilde und sich die beiden daher nicht wesentlich unterscheiden. Der Raum, so Descartes, sei die Gesamtheit der Erstreckungen und Positionen der Körper relativ zueinander dar, und Bewegung gebe es nur als Veränderung der Abstände und Anordnung der Körper untereinander. Einen wahrhaft unbewegten Ort dagegen gebe es nicht.
Leibniz hat diesen Gedanken aufgenommen und zu einer systematischen Theorie des Raumes ausgebaut. Auch seine kausale Theorie der Zeitfolge ist tatsächlich Teil dieses umfassenden relationalen Ansatzes.
Für Descartes und Leibniz war der Raum die Gesamtheit aller möglichen Anordnungen von Dingen, die gleichzeitig existieren.
Völlig anders Leibniz: Für ihn gab es diesen Behälter nicht. Er hielt den Raum ebenso wie die Zeit für etwas rein Relationales:
- Raum sei einfach nur eine Ordnung des Neben-einander-Bestehens von Objekten: die Gesamtheit der relativen Anordnungen der Körper,
- wohingegen Zeit nur als ein Auf-einander-Folgen von Ereignissen existiere.
Die Ursprünge solch einer relationalen Theorie von Raum und Zeit gehen auf Decartes (1596-1650) zurück. In seinen Prinzipien der Philosophie vertrat er die Ansicht, dass Ausdehnung das kennzeichnende Merkmal von Materie und Raum gleichermaßen bilde und sich die beiden daher nicht wesentlich unterscheiden. Der Raum, so Descartes, sei die Gesamtheit der Erstreckungen und Positionen der Körper relativ zueinander dar, und Bewegung gebe es nur als Veränderung der Abstände und Anordnung der Körper untereinander. Einen wahrhaft unbewegten Ort dagegen gebe es nicht.
Leibniz hat diesen Gedanken aufgenommen und zu einer systematischen Theorie des Raumes ausgebaut. Auch seine kausale Theorie der Zeitfolge ist tatsächlich Teil dieses umfassenden relationalen Ansatzes.
Beitrag 0-440
ART und Quantenphysik sind hintergrundunabhäbgige Weltmodelle
Zur Hintergrundunabhängigkeit von ART und Quantenphysik
Die wichtigste begriffliche Eigenschaft der allgemeinen Relativitätstheorie (ART) besteht in der sogenannten Hintergrundunabhängigkeit.
Man versteht darunter die Tatsache, dass in der ART den Raum-Zeit-Koordinaten überhaupt keine physikalische Bedeutung mehr zukommt, sondern nur noch den Beziehungen zwischen den Feldern auf der Raum-Zeit, zu denen auch das metrische Feld gehört, welches das Gravitationsfeld darstellt.
Dies hat damit zu tun, dass es in der allgemeinen Relativitätstheorie überhaupt keine absoluten Größen mehr gibt, da auch die Metrik — im Gegensatz zur speziellen Relativitätstheorie (SRT) — in der ART zu einer dymamischen Größe wird.
Das aber bedeutet, dass die Raumzeit ohne die in ihr enthaltenen dynamischen Objekte gar nicht existiert.
Dennoch kennt die ART — in einem relationalen Sinne — räumlich-kausale Strukturen, da in ihr ja — als zentrale, dynamische Größen — Felder auf der Raum-Zeit beschrieben werden.
Die Quantentheorie — in ihrer der abstrakten Hilbertraum-Formulierung — geht noch weiter: Sie verzichtet auf Begriffe wie Raum, Körper, Feld, Teilchen, Bewegung, Wechselwirkung, Masse oder Ladung. Nur die Zeit muss beibehalten werden.
Und so kommt dem Raum in der Quantentheorie noch weniger Bedeutung zu als in der ART.
Quelle: Martin Immanuel Kober (2018) in Fortführung des Ansatzes der Ur-Alternativen von Carl Friedrich v. Weizsäcker
Die wichtigste begriffliche Eigenschaft der allgemeinen Relativitätstheorie (ART) besteht in der sogenannten Hintergrundunabhängigkeit.
Man versteht darunter die Tatsache, dass in der ART den Raum-Zeit-Koordinaten überhaupt keine physikalische Bedeutung mehr zukommt, sondern nur noch den Beziehungen zwischen den Feldern auf der Raum-Zeit, zu denen auch das metrische Feld gehört, welches das Gravitationsfeld darstellt.
Dies hat damit zu tun, dass es in der allgemeinen Relativitätstheorie überhaupt keine absoluten Größen mehr gibt, da auch die Metrik — im Gegensatz zur speziellen Relativitätstheorie (SRT) — in der ART zu einer dymamischen Größe wird.
Dennoch kennt die ART — in einem relationalen Sinne — räumlich-kausale Strukturen, da in ihr ja — als zentrale, dynamische Größen — Felder auf der Raum-Zeit beschrieben werden.
Die Quantentheorie — in ihrer der abstrakten Hilbertraum-Formulierung — geht noch weiter: Sie verzichtet auf Begriffe wie Raum, Körper, Feld, Teilchen, Bewegung, Wechselwirkung, Masse oder Ladung. Nur die Zeit muss beibehalten werden.
Und so kommt dem Raum in der Quantentheorie noch weniger Bedeutung zu als in der ART.
Quelle: Martin Immanuel Kober (2018) in Fortführung des Ansatzes der Ur-Alternativen von Carl Friedrich v. Weizsäcker
Beitrag 0-49
Was sich heute zur Natur der Raumzeit sagen — aber auch f r a g e n — lässt
Warum man die Natur der Raumzeit heute noch als unentschieden sehen muss
Die relationale — der Ansicht von Decartes, Leibniz, Mach und Einstein entsprechenden — Rückführung der Raumzeitpunkte auf die Anordnung materieller Objekte untereinander hat zur Folge, dass es unbesetzte Raumzeitpunkte, leeren Raum also, nicht geben kann.
Die substanzialistische Ansicht aber, dass der Raum eigenständig existiere, setzt die Annahme der Existenz solche unbesetzter Raumzeitpunkte geradezu voraus.
Aus meiner [ Gebhard Greiters ] Sicht heraus, scheint mir diese Argumentation nicht so ganz überzeugend, denn wo es wellenartig sich auf- und abbauendes Kraftpotential gibt, muss es doch eigentlich auch als Anwesenheit von Energie gedeutet werden. Wie also unterscheidet die sich von der durch den Energie-Impuls-Tensor beschriebenen?
Die relationale — der Ansicht von Decartes, Leibniz, Mach und Einstein entsprechenden — Rückführung der Raumzeitpunkte auf die Anordnung materieller Objekte untereinander hat zur Folge, dass es unbesetzte Raumzeitpunkte, leeren Raum also, nicht geben kann.
Die substanzialistische Ansicht aber, dass der Raum eigenständig existiere, setzt die Annahme der Existenz solche unbesetzter Raumzeitpunkte geradezu voraus.
Martin Carrier (S. 205-206 seines Buches Raum-Zeit, de Gruyter 2009) schreibt:
Vor dem Hintergrund der ART lautet die wesentliche Frage, ob Raumzeitmetrik gik und Geodätenstruktur zur Raumzeit oder zur Materie zu zählen sind.
Die Feldgleichungen verknüpfen den Energie-Impuls-Tensor Tik mit einem Ausdruck, der die über Metrik und Geodäten gegebene physikalische Geometrie repräsentiert. So gesehen ist die Metrik Teil der Raumzeit, nicht aber der Materie.
Gegen den Relationalismus aber spricht, dass die Feldgleichungen physikalisch signifikante Vakuumlösungen enthalten (denn auch bei verschwindender Materie und Energie ergeben sich definitive metrische Felder und Geodätenstrukturen als Lösungen). Es handelt sich dabei insbesondere um Gravitationswellen, also um sich fortplanzende Schwingungen des metrischen Feldes.
Danach kann auch dort Raumzeit, nämlich ein nicht verschwindendes metrisches Feld gik vorliegen, wo keine Materie ist, genauer: wo der Energie-Impuls-Tensor verschwindet.
So führt z.B. der Kollaps eines Sternes zur Emission von Gravitationswellen, Sie entfernen sich vom Ort des Geschehens wie Wasserwellen von einem ins Wasser geworfenen Stein. Weit ab vom Ereignis mag keinerlei materieller Rest des Zusammenbruchs mehr vorhanden sein; in den Gravitationswellen aber manifestiert sich gleichwohl eine definitive Metrik.
Somit realisieren Gravitationswellen leere Raumzeit-Punkte, und d i e s e r Befund stützt die Vorstellung einer substanzialstischen Raumzeit.
Aus meiner [ Gebhard Greiters ] Sicht heraus, scheint mir diese Argumentation nicht so ganz überzeugend, denn wo es wellenartig sich auf- und abbauendes Kraftpotential gibt, muss es doch eigentlich auch als Anwesenheit von Energie gedeutet werden. Wie also unterscheidet die sich von der durch den Energie-Impuls-Tensor beschriebenen?
Beitrag 0-47
Wie sich der Geometrie-Begriff entwickelt hat: Von Euklid bis hin zu Riemann und Einstein
Wie sich der Geometrie-Begriff entwickelt hat (bis hin zu dem der ART)
Über fast zwei Jahrtausende hinweg war die Euklidische Geometrie die einzig bekannte. Nach anderen Geometrien zu suchen kam lange Zeit niemand in den Sinn, denn einerseits entspricht sie gut unserer Erfahrungswelt und noch Euklid (ca. 365-300 v.Chr) hatte sie von Anfang an fest verankert in 5 Postulaten, auf die er all seine Lehrsätze stützte (und die suggerierten, dass Geometrie stets nur im Kontext einer flachen Ebene Sinn machen).
Hierzu zählten Forderungen so einfacher Art, dass zwischen je zwei Punkten eine Gerade gezogen werden kann und jede Strecke zu einer Geraden verlängert werden kann. Nur Euklids fünftes, letztes Postulat — in dem er verlangt, dass es durch einen Punkt P der nicht auf einer gegebenen Geraden G liegt stets eine andere Gerade gebe, die parallel zu G ist — hat den Mathematikern zunehmend Kopfzerbrechen bereitet: Sie vermuteten, dass dieses so vergleichsweise komplizierte Postulat schon Folge der anderen sein könnte.
Dies zu beweisen allerdings gelang niemand. Kein Wunder, denn Bolyai (1802-1860) und unabhängig von ihm auch Lobaschewski (1792-1856) und schließlich Gauss (1777-1855) fanden schließlich, dass auch andere Fassungen des Parallelenaxioms denkbar und ebenfalls mit den übrigen 4 Axiomen verträglich sind: Statt die Existenz genau einer Parallele zu G durch P kann man auch die Existenz gar keiner oder die Existenz von mindestens zwei fordern.
Diese Einsicht markierte die Entdeckung zweier Familien Nicht-Euklidischer Geometrie. Man nennt sie Geometrien elliptischer bzw. hyperbolischer Art je nachdem ob sie gar keine oder mehrere Parallen zu G durch P gestatten.
Bernhard Riemann — ein Schüler von Gauss — konnte schließlich beweisen, dass sie und auch die Geometrie Euklidischer Art sämtlich Spezialfälle einer noch allgemeineren geometrischen Theorie sind: einer, die man heute die Riemannsche Geometrie nennt (noch etwas allgemeinere entstanden ab 1920).
Ihr Hauptcharakteristikum — im Nachhinein eigentlich nicht verwunderlich — ist, dass es sich um Geometrien handelt, die erlauben, dass der betrachtete Raum ortsabhängig unterschiedliche geometrische Charakterista aufweist.
Und tatsächlich: Denkt man z.B. daran, dass die Landschaft in Norddeutschland kaum Krümmung aufweist, viel weniger bizarre jedenfalls als die Landschaft z.B. in den Alpen oder im Himalaya, und dass das Krümmungsverhalten der Landschaft auf dem Weg von hier nach dort sich nur schrittweise abändert, so kann man gut nachvollziehen, dass
Den Typ mathematischer Struktur, der erlaubt, Räume mit solch allgemeinem Krümmungsverhalten formal sauber zu beschreiben nennt man Riemannsche Mannigfaltigkeit .
Gauss hatte versucht, solche Räume durch Teilmengen je eines Raumes noch höherer Dimension zu modellieren. Riemann aber fiel auf, dass Vieles einfacher wird, wenn man statt der Einbettung des zu beschreeibenden Raumes R in einen noch höher dimensionalen Raum sog. Tangentenräume heranzieht: Jeder von ihnem ist genau einem Punkt P von R zugeordnet, hat Euklidische Geometrie (d.h. die denkbar einfachste) und approximiert über sie die Geometrie von R um P herum beliebig gut — dann jedenfalls, wenn man sich auf eine entsprechend kleine Umgebung von P beschränkt.
Es hat dann natürlich auch jede dieser Umgebungen U(P) ihr eigenes Koordinatensystem, sein Urprung ist P selbst. Ein den gesamten Raum R umspannendes, globales Koordinatensystem braucht n i c h t zu existieren.
Mehr dazu lese man nach in Wikipedia.
Über fast zwei Jahrtausende hinweg war die Euklidische Geometrie die einzig bekannte. Nach anderen Geometrien zu suchen kam lange Zeit niemand in den Sinn, denn einerseits entspricht sie gut unserer Erfahrungswelt und noch Euklid (ca. 365-300 v.Chr) hatte sie von Anfang an fest verankert in 5 Postulaten, auf die er all seine Lehrsätze stützte (und die suggerierten, dass Geometrie stets nur im Kontext einer flachen Ebene Sinn machen).
Hierzu zählten Forderungen so einfacher Art, dass zwischen je zwei Punkten eine Gerade gezogen werden kann und jede Strecke zu einer Geraden verlängert werden kann. Nur Euklids fünftes, letztes Postulat — in dem er verlangt, dass es durch einen Punkt P der nicht auf einer gegebenen Geraden G liegt stets eine andere Gerade gebe, die parallel zu G ist — hat den Mathematikern zunehmend Kopfzerbrechen bereitet: Sie vermuteten, dass dieses so vergleichsweise komplizierte Postulat schon Folge der anderen sein könnte.
Dies zu beweisen allerdings gelang niemand. Kein Wunder, denn Bolyai (1802-1860) und unabhängig von ihm auch Lobaschewski (1792-1856) und schließlich Gauss (1777-1855) fanden schließlich, dass auch andere Fassungen des Parallelenaxioms denkbar und ebenfalls mit den übrigen 4 Axiomen verträglich sind: Statt die Existenz genau einer Parallele zu G durch P kann man auch die Existenz gar keiner oder die Existenz von mindestens zwei fordern.
Diese Einsicht markierte die Entdeckung zweier Familien Nicht-Euklidischer Geometrie. Man nennt sie Geometrien elliptischer bzw. hyperbolischer Art je nachdem ob sie gar keine oder mehrere Parallen zu G durch P gestatten.
Bernhard Riemann — ein Schüler von Gauss — konnte schließlich beweisen, dass sie und auch die Geometrie Euklidischer Art sämtlich Spezialfälle einer noch allgemeineren geometrischen Theorie sind: einer, die man heute die Riemannsche Geometrie nennt (noch etwas allgemeinere entstanden ab 1920).
Ihr Hauptcharakteristikum — im Nachhinein eigentlich nicht verwunderlich — ist, dass es sich um Geometrien handelt, die erlauben, dass der betrachtete Raum ortsabhängig unterschiedliche geometrische Charakterista aufweist.
Und tatsächlich: Denkt man z.B. daran, dass die Landschaft in Norddeutschland kaum Krümmung aufweist, viel weniger bizarre jedenfalls als die Landschaft z.B. in den Alpen oder im Himalaya, und dass das Krümmungsverhalten der Landschaft auf dem Weg von hier nach dort sich nur schrittweise abändert, so kann man gut nachvollziehen, dass
- Euklidische Geometrie dem einfachsten Fall entspricht: Sie ist die Geometrie einer absolut flachen, nirgendwo gekrümmten Ebene (bzw. eines nirgendwo gekrümmten Raumes beliebiger Dimension).
- Elliptische Geometrie oder hyperbolische Geometrie ist stets Geometrie eines überall in gleicher Weise gekrümmten Raumes (ee könnte Kugeloberfläche im elleptischen Fall oder Oberfäche eines Sattels im hyperbolischen
Fall sein).
- Riemannsche Geometrie schließlich kann ortsabhängig variierende Krümmung ganz unterschiedlicher Stärke beschreiben.
Den Typ mathematischer Struktur, der erlaubt, Räume mit solch allgemeinem Krümmungsverhalten formal sauber zu beschreiben nennt man Riemannsche Mannigfaltigkeit .
Gauss hatte versucht, solche Räume durch Teilmengen je eines Raumes noch höherer Dimension zu modellieren. Riemann aber fiel auf, dass Vieles einfacher wird, wenn man statt der Einbettung des zu beschreeibenden Raumes R in einen noch höher dimensionalen Raum sog. Tangentenräume heranzieht: Jeder von ihnem ist genau einem Punkt P von R zugeordnet, hat Euklidische Geometrie (d.h. die denkbar einfachste) und approximiert über sie die Geometrie von R um P herum beliebig gut — dann jedenfalls, wenn man sich auf eine entsprechend kleine Umgebung von P beschränkt.
Es hat dann natürlich auch jede dieser Umgebungen U(P) ihr eigenes Koordinatensystem, sein Urprung ist P selbst. Ein den gesamten Raum R umspannendes, globales Koordinatensystem braucht n i c h t zu existieren.
Mehr dazu lese man nach in Wikipedia.
Beitrag 2051-1
Grenzen der Anwendbarkeit der SRT (und teilweise auch der ART)
Wer die SRT anwenden möchte, sollte bedenken:
Die Anwendbarkeit der SRT ist an gewisse Voraussetzungen geknüpft, die man nicht aus dem Auge verlieren sollte (und die stets nur annäherend gegeben sind, auf keinen Fall also über unser gesamtes Universum hinweg so genau, dass die SRT über beliebige Entfernungen hin brauchbare Aussagen machen würde).
Diese Voraussetzungen sind:
Da in unserer Raumzeit alle masse-behafteten Objekte Gravitationskräften unterliegen, die durch andere solcher Objekte hervorgerufen werden, und da diese Kräfte sich wohl nur ausnahmsweise und sicher nur über extrem kurze Zeit hinweg an dem einen oder anderen Ort zu Null ergänzen, ist die wichtigste Voraussetzung für die Anwendbarkeit der SRT i.A. wirklich voll so gut wie nie und nirgenwo gegeben.
Mit anderen Worten: Die SRT ist eine eher lokale Theorie (weswegen ich sie denn auch — anders als Okotombrok — im Kontext des Themas 2049-24 gar nicht erst zur Sprache gebracht hätte.
Wir könnten jetzt aber mal der Frage nachgehen, WIE lokal die SRT denn eigentlich ist, d.h. welche Eigenschaften eine Region der Raumzeit haben muss, damit die SRT für Gegenstände in jener Region Aussagen macht, die nicht allzu ungenau sind.
Eines steht fest (wenn wir daran denken, dass Gravitationskräfte sämtliche Objekte beschleunigen, die nicht schon mit Lichtgeschwindigkeit unterwegs sind):
Da die Raumzeit der ART eine differenzierbare Mannigfaltigkeit ist, können wir nur sagen:
All das berücksichtigt noch gar nicht die Tatsache, dass unsere wirkliche Welt im ganz Kleinen — gemeint ist: in einer Größenordnung, die sich der Plancklänge nähert — hinsichlich ihrer geometrischen Struktur selbst durch die ART ganz und gar nicht zutreffend beschrieben ist. Dort nämlich ändert sich die Topologie des Raumes zeitlich gesehen noch weit schneller und weit dramatischer. In dieser Größenordnung die SRT noch anwenden zu wollen, würde zu rein gar nichts führen.
Wer mehr zu all dem wissen möchte, sollte versuchen, zu verstehen, was in Consequences of Spacetime Topology gesagt wird oder in den Papieren, die dort im Literaturverzeichnis genannt sind.
Gebhard Greiter (grtgrt)
Die Anwendbarkeit der SRT ist an gewisse Voraussetzungen geknüpft, die man nicht aus dem Auge verlieren sollte (und die stets nur annäherend gegeben sind, auf keinen Fall also über unser gesamtes Universum hinweg so genau, dass die SRT über beliebige Entfernungen hin brauchbare Aussagen machen würde).
Diese Voraussetzungen sind:
- Es muss ein Inertialsystem geben, in das sich alle betrachteten Objekte gemeinsam einordnen — und zwar so, dass sie unter dieser Einordnung als NICHT beschleunigt erscheinen.
- Es muss uns reichen, Aussagen zu erhalten, die nicht beobachter-neutral sind.
Da in unserer Raumzeit alle masse-behafteten Objekte Gravitationskräften unterliegen, die durch andere solcher Objekte hervorgerufen werden, und da diese Kräfte sich wohl nur ausnahmsweise und sicher nur über extrem kurze Zeit hinweg an dem einen oder anderen Ort zu Null ergänzen, ist die wichtigste Voraussetzung für die Anwendbarkeit der SRT i.A. wirklich voll so gut wie nie und nirgenwo gegeben.
Mit anderen Worten: Die SRT ist eine eher lokale Theorie (weswegen ich sie denn auch — anders als Okotombrok — im Kontext des Themas 2049-24 gar nicht erst zur Sprache gebracht hätte.
Wir könnten jetzt aber mal der Frage nachgehen, WIE lokal die SRT denn eigentlich ist, d.h. welche Eigenschaften eine Region der Raumzeit haben muss, damit die SRT für Gegenstände in jener Region Aussagen macht, die nicht allzu ungenau sind.
Eines steht fest (wenn wir daran denken, dass Gravitationskräfte sämtliche Objekte beschleunigen, die nicht schon mit Lichtgeschwindigkeit unterwegs sind):
- Je weniger Himmelskörper sich in jener Region befinden, desto besser wird die SRT dort anwendbar sein.
- Umgekehrt: Kaum anwendbar sein wird die SRT in der Nähe eines Schwarzen Loches oder gar im Inneren seines Ereignishorizontes. Rein mathematische Betrachtungen sagen uns noch mehr: Die SRT ist nicht anwendbar in naher Umgebung irgend einer Singularität der Raumzeit, als z.B. auch nicht zu Beginn des Urknalls und allzu kurz danach.
Da die Raumzeit der ART eine differenzierbare Mannigfaltigkeit ist, können wir nur sagen:
- Jeder nicht-singuläre Punkt x der Raumzeit hat mindestens eine topologische Umgebung U(x), welche isomorh ist zu einer geeigneten tologischen Umgebung des Ursprungs des normalen 4-dimensionen metrischen (reellen) Raumes, genauer: des Minkowski-Raumes im Sinne der SRT.
- Sei nun V(x) die Vereinigung aller Umgebungen von x mit dieser Eigenschaft. Dann ist auch V(x) selbst die größte solche Umgebung, und maximal nur in ihr können wir uns ein kartesisches Koordinatensystem vorstellen, in das sich alle Punkte aus V(x) gemeinsam einordnen. Problem aber: Form und Größe von V(x) sind zeitlich variabel — mindestens in gewissem Ausmaß, das wiederum davon abhängt, wie turbulent es um x herum zugeht.
All das berücksichtigt noch gar nicht die Tatsache, dass unsere wirkliche Welt im ganz Kleinen — gemeint ist: in einer Größenordnung, die sich der Plancklänge nähert — hinsichlich ihrer geometrischen Struktur selbst durch die ART ganz und gar nicht zutreffend beschrieben ist. Dort nämlich ändert sich die Topologie des Raumes zeitlich gesehen noch weit schneller und weit dramatischer. In dieser Größenordnung die SRT noch anwenden zu wollen, würde zu rein gar nichts führen.
Wer mehr zu all dem wissen möchte, sollte versuchen, zu verstehen, was in Consequences of Spacetime Topology gesagt wird oder in den Papieren, die dort im Literaturverzeichnis genannt sind.
Gebhard Greiter (grtgrt)
Beitrag 2051-3
-
Ja, Hans-m, genau so meine ich das.
Mit zu berücksichtigen ist allerdings, dass in extremen Szeanrios — wie etwa im Inneren aller Schwarzen Löcher oder im Quantenschaum — die Aussagen i d e a l e r Betrachtung beliebig weit von r e a l e n Gegebenheiten abweichen können.
Die Abweichung, mit der man zu rechnen hat, dort nicht abschätzen zu können, wird zum Problem.
Gruß, grtgrt
Hans-m aus 2051-2:
Ich glaube du sprichst hier den Unterscheid zwischen idealer und realer Betrachtung eines Inertialsystem an.
Ein ideales Inertialsysem ist absolut unbeschleunigt, unterliegt keiner Gravitation und keinen sonstige Kräften.
Ein ideales System kann dem realen System nur annähernd gleichkommen.
Ja, Hans-m, genau so meine ich das.
Mit zu berücksichtigen ist allerdings, dass in extremen Szeanrios — wie etwa im Inneren aller Schwarzen Löcher oder im Quantenschaum — die Aussagen i d e a l e r Betrachtung beliebig weit von r e a l e n Gegebenheiten abweichen können.
Die Abweichung, mit der man zu rechnen hat, dort nicht abschätzen zu können, wird zum Problem.
Gruß, grtgrt
Beitrag 2051-5
-
Richtig, Hans-m, das kommt noch dazu.
Mir kam es aber darauf an, zu sagen, dass mit zunehmender Nähe zur Singularität die Ungenauigkeit, die ich mir beim Nutzen des nur näherungsweise gültigen Modells einhandle, sehr schnell überhaupt nicht mehr abschätzbar wird.
Hans-m aus 2051-4:Grtgrt aus 2051-3:
Mit zu berücksichtigen ist allerdings, dass in extremen Szeanrios — wie etwa im Inneren aller Schwarzen Löcher oder im Quantenschaum — die Aussagen
i d e a l e r Betrachtung beliebig weit von r e a l e n Gegebenheiten abweichen können.
Fakt ist: Worüber ich nix weiss, kann ich auch nix berechnen.
Alles was sich innerhalb des Ereignishorizontes eines SL abspielt, ist für den Betrachter ausserhalb nicht ersichtlich.
Richtig, Hans-m, das kommt noch dazu.
Mir kam es aber darauf an, zu sagen, dass mit zunehmender Nähe zur Singularität die Ungenauigkeit, die ich mir beim Nutzen des nur näherungsweise gültigen Modells einhandle, sehr schnell überhaupt nicht mehr abschätzbar wird.
Beitrag 2016-45
Macht sie wirklich Raum und Zeit ununterscheidbar?
Nochmals zurück zur Raumzeit im Sinne der ART:
Mir ist schon bekannt, dass Wikipedia und auch andere Quellen sagen:
Ein Beispiel für eine solche "Vermischung" ist mir bisher nicht über den Weg gelaufen.
Wer kann mir sagen, wo ich ein möglichst einfaches tatsächlich nachgerechnet finden kann?
Nochmals zurück zur Raumzeit im Sinne der ART:
Mir ist schon bekannt, dass Wikipedia und auch andere Quellen sagen:
Zitat von Wikipedia:
Die Raumzeit bezeichnet in der Relativitätstheorie die Vereinigung von Raum und Zeit in einer einheitlichen vierdimensionalen Struktur mit speziellen Eigenschaften (z. B. "Kausalität"), in welcher die räumlichen und zeitlichen Koordinaten bei Transformationen in andere Bezugssysteme miteinander vermischt werden können.
Ein Beispiel für eine solche "Vermischung" ist mir bisher nicht über den Weg gelaufen.
Wer kann mir sagen, wo ich ein möglichst einfaches tatsächlich nachgerechnet finden kann?
Beitrag 2016-49
-
Siehst du, E...,
das genau ist der Punkt. Auch ich kann weder an den von dir genannten Stellen noch irgendwo sonst, so eine "Vermischmaschine" erkennen.
Gruß, grtgrt
E... aus 2016-47:
Aber eine "Vermischmaschine" gibt es da nicht.
Siehst du, E...,
das genau ist der Punkt. Auch ich kann weder an den von dir genannten Stellen noch irgendwo sonst, so eine "Vermischmaschine" erkennen.
Gruß, grtgrt
Beitrag 2031-49
Über die hohe Genauigkeit von Einsteins Gravitationstheorie
Hi E...,
man hat eben erst (2013) einen Weg gefunden, die Theorie Einsteins zur Gravitation — die Allgemeine Relativitätstheorie — auf eine Art und Weise zu überprüfen, die bisher nicht möglich war. Die neuen Beobachtungen stimmen genau mit den Vorhersagen der Allgemeinen Relativitätstheorie überein und sind nicht konsistent mit einigen alternativen Theorien.
Mehr dazu findest Du in einer Pressemitteilung des ESO mit dem Titel » Einstein behält recht «.
PS: Gravitationswellen kosmischen Ursprungs werden von der Allgemeiner Relativitätstheorie vorhergesagt, konnten aber bis heute trotz zahlreicher experimenteller Tests nicht direkt nachgewiesen werden. Einen ersten (wenigstens indirekten) Hinweis auf die Existenz dieser Wellen hat 1974 Russell Hulse entdeckt: Es ist der Doppelpulsar PSR 1913+16. Die Variationen in der Umlaufbahn dieses Doppelsystems stimmen exakt mit den Vorhersagen der Allgemeinen Relativitätstheorie zur Abstrahlung von Gravitationswellen überein. Hulse erhielt 1993 für diese Entdeckung den Nobelpreis für Physik.
Der jetzt (2013) entdeckte Pulsar PSR J0348+0432 ist nur ein zweites Beispiel dieser Art — aber natürlich willkommene Bestätigung dafür, dass man Hulses Entdeckung richtig gedeutet hat.
Gruß, grtgrt
E... aus 2031-42:
Zitat aus einem Standardwerk über Galaxien-Dynamik von
J. Binney und S. Tremaine: >Galactic Dynamics< ISBN 0-691-08445-9 von 1988 der Princeton University Press, Seite 635
Zitat:Bisher wurde angenommen, dass die allgemeine Relativitätstheorie bzw. die Newtonsche Gravitation auf großen Skalen gelten. Tatsächlich gibt es aber wenig oder gar keine direkten Belege dafür, dass die konventionellen Gravitationstheorien auch auf Skalen korrekt sind, die z.B. viel größer als ein Lichtjahr sind. Die Newtonsche gravitation funktioniert ausgezeichnet auf Skalen von 1012 Metern, also im Sonnensystem. Es ist aber hauptsächlich die Eleganz der Allgemeinen Relativitätstheorie mit ihren erfolgreichen Vorhersagen im Sonnensystem, die uns zu der gewaltigen Extrapolation auf 1021 - 1026 Meter führt.
Auf der folgenden Seite äußert sich Pavel Kroupa vom Argelander-Institut für Astronomie der Universität Bonn, der die Untersuchung gemeinsam mit Kollegen aus Deutschland, Österreich und Australien durchgeführt hat.
http://www.weltderphysik.de/gebiet/astro/news/2009/...
Hi E...,
man hat eben erst (2013) einen Weg gefunden, die Theorie Einsteins zur Gravitation — die Allgemeine Relativitätstheorie — auf eine Art und Weise zu überprüfen, die bisher nicht möglich war. Die neuen Beobachtungen stimmen genau mit den Vorhersagen der Allgemeinen Relativitätstheorie überein und sind nicht konsistent mit einigen alternativen Theorien.
Mehr dazu findest Du in einer Pressemitteilung des ESO mit dem Titel » Einstein behält recht «.
PS: Gravitationswellen kosmischen Ursprungs werden von der Allgemeiner Relativitätstheorie vorhergesagt, konnten aber bis heute trotz zahlreicher experimenteller Tests nicht direkt nachgewiesen werden. Einen ersten (wenigstens indirekten) Hinweis auf die Existenz dieser Wellen hat 1974 Russell Hulse entdeckt: Es ist der Doppelpulsar PSR 1913+16. Die Variationen in der Umlaufbahn dieses Doppelsystems stimmen exakt mit den Vorhersagen der Allgemeinen Relativitätstheorie zur Abstrahlung von Gravitationswellen überein. Hulse erhielt 1993 für diese Entdeckung den Nobelpreis für Physik.
Der jetzt (2013) entdeckte Pulsar PSR J0348+0432 ist nur ein zweites Beispiel dieser Art — aber natürlich willkommene Bestätigung dafür, dass man Hulses Entdeckung richtig gedeutet hat.
Gruß, grtgrt
Beitrag 2035-25
Wie sich in der Relativitätstheorie Geschwindigkeiten addieren
Hallo Struktron,
herzlich wilkommen im Forum.
Die Formel zum Addieren relativistischer Geschwindigkeiten lautet:
vr = ( v1 + v2 )/( 1 + (v1v2)/c2 )
wobei vr die resultierende Geschwindigkeit meint und v1 und v2 die zu addierenden Geschwindigkeiten.
Setzt man nun für v1 und v2 c ein, so lautet das Ergebnis c und nicht 2c.
mfg okotombrok
herzlich wilkommen im Forum.
Struktron aus 2035-21:Nun entfernen sich die Satelliten so voneinander, dass unsere Signale genau in gegengesetzte Richtung fliegen müssen, um die Satelliten zu erreichen. Bei der Ankunft sind beide wiederum von uns genau 300.000 km entfernt. Die Ankunftsmeldung kommt auch wieder nach einer Sekunde.
Mit welcher Geschwindigkeit haben sich die Wellenfronten voneinander entfernt?
Die Formel zum Addieren relativistischer Geschwindigkeiten lautet:
wobei vr die resultierende Geschwindigkeit meint und v1 und v2 die zu addierenden Geschwindigkeiten.
Setzt man nun für v1 und v2 c ein, so lautet das Ergebnis c und nicht 2c.
mfg okotombrok
Beitrag 2035-40
Kosmologie kennt zweierlei Arten von Geschwindigkeit und Beschleunigung
Hi Okotombrok,
nachdem Henry mich so gründlich missverstanden hat, will ich meine Festellung und meine Frage aus Beitrag 2035-31 hier nochmals deutlicher formulieren:
Die Physik unterscheidet — ganz anders als die Mathematik —
Deine Aussage in Beitrag 2035-24 verstehe ich so, dass Du sagen wolltest:
Nun also meine Frage:
Nach allem, was ich weiß, kennt die ART beide Arten von Beschleunigung und Geschwindigkeit. Wie aber unterscheidet sie zwischen ihnen?
Gruß, grtgrt
Hi Okotombrok,
nachdem Henry mich so gründlich missverstanden hat, will ich meine Festellung und meine Frage aus Beitrag 2035-31 hier nochmals deutlicher formulieren:
Die Physik unterscheidet — ganz anders als die Mathematik —
- zwei verschiedene Arten von Beschleunigung und
- korrespondierend dazu auch zwei verschiedene Arten von Geschwindigkeit.
Deine Aussage in Beitrag 2035-24 verstehe ich so, dass Du sagen wolltest:
- Beschleunigung, die Trägheitskräfte zu überwinden hat, kann nur zu Geschwindigkeiten v < c führen.
- Beschleunigung, die durch "dunkle Energie" hervorgerufen wird, erzeugt keine Trägheitskraft und kann zu Geschwindigkeiten führen, die größer als die Lichtgeschwindigkeit sind.
Nun also meine Frage:
Nach allem, was ich weiß, kennt die ART beide Arten von Beschleunigung und Geschwindigkeit. Wie aber unterscheidet sie zwischen ihnen?
Gruß, grtgrt
Beitrag 2089-11
Krümmung des Raumes und (dort) von Null verschiedenes Energiepotential sind ein und dasselbe
Hallo Henry,
ich würde eher sagen, auch nach der ART bleibt die Gravitation als eine der vier Grundkräfte der Natur erhalten.
Vielmehr verleiht die Krümmung der Raumzeit den Körpern Masse und die Masse der Körper verursacht die Krümmung der Raumzeit. Was ich an dieser Konstruktion nicht verstehe ist, dass es für mich wie ein Zirkelschluss erscheint.
MfG
Harti�
Henry in 2089-7:aber noch bedeutender ist die revolutionäre neue Auffassung der Gravitation nicht als Kraft, sondern als Krümmung der Raumzeit.
Hallo Henry,
ich würde eher sagen, auch nach der ART bleibt die Gravitation als eine der vier Grundkräfte der Natur erhalten.
Vielmehr verleiht die Krümmung der Raumzeit den Körpern Masse und die Masse der Körper verursacht die Krümmung der Raumzeit. Was ich an dieser Konstruktion nicht verstehe ist, dass es für mich wie ein Zirkelschluss erscheint.
MfG
Harti�
Beitrag 2089-14
-
Hallo Hans-m,
eine absolut vollständige Antwort kann ich dir sicher nicht geben, wohl aber einige Denkanstöße:
In der Hoffnung, Dir hiermit gedient zu haben,
Gruß, grtgrt
Hans-m in 2089-13:
Wie aber definiere ich nun die Energiepotenziale und wie die daraus resultierenden Raumkrümmungen?
Wohlgemerkt, ich meine hier nicht die Masse von Objekt 1,2 oder 3, sondern die kinetische Energie der Objekte untereinander.
Solange die Objekte in Bewegung sind habe ich eine Längenkontraktion. diese entfällt aber, wenn sich die Objekte nicht mehr relativ zueinader bewegen.
Hallo Hans-m,
eine absolut vollständige Antwort kann ich dir sicher nicht geben, wohl aber einige Denkanstöße:
- Zur letzten Aussage deines Zitats sei gesagt: Die Längenkontraktion existiert nur aus S i c h t von relativ zum Objekt sich bewegender Beobachter.
- BEWEIS: Die Tatsache, dass es Beobachter geben kann, die sich unterschiedlich schnell relativ zum betrachteten Objekt bewegen — also unterschiedlich starke Längenkontraktion sehen —, zeigt ganz klar, dass die Längenkontraktion nur in der Wahrnehmung dieser Beobachter existiert, n i c h t aber in der Struktur des Raumes vorhanden sein kann (!).
- Was Wege zur Berechnung des Potentialfeldes betrifft, geht mir Folgendes durch den Kopf:
- Einstein hat gezeigt, dass sich Kräfte, die ein Objekt beschleunigen, von Gravitationskräften (der Kraft also, die der Gegenwart von Energiepotential geschuldet ist) in keiner Weise unterscheiden lassen. Das scheint mir auch irgendwie logisch zu sein, denn Ursache aller Beschleunigung ist Kraft, d.h. die Gegenwart von Energiepotential.
- Jede an einem Ort X wirkende Kraft lässt sich beschreiben als Vektor k(X), der bestimmte Richtung und bestimmte Länge hat. Die Summe aller Kräfte — die Summe aller Energiepotentiale also, die sich dem Ort X zuordnen — ist gegeben als Summe dieser Vektoren.
- Damit, so denke ich, ist deine Frage, wie sich denn das einem Ort X zugeordnete Energiepotential berechnen lässt, wenigstens im Prinzip geklärt.
- Wer es wirklich berechnen will, wird dennoch seine Schwierigkeiten haben, denn:
- erstens muss er ja feststellen, welche Kräfte wirken (d.h. welche Kraftquellen da sind und wie weit weg von Stelle X sie sich befinden)
- zweitens muss berücksichtigt werden, dass diese Kraftquellen sich i.A. relativ zu X bewegen, und
- drittens wird in die Berechnung irgendwo eingehen müssen, dass nicht alle 4 Grundkräfte sich identisch verhalten.
In der Hoffnung, Dir hiermit gedient zu haben,
Gruß, grtgrt
Beitrag 1997-26
Raumzeit und ART vs SRT
Hallo Henry,
richtig, genau das wollte ich mit dem Schlagwort "Union zwischen Raumzeit und Materie" zum Ausdruck bringen. Also, volle Übereinstimmung.
M.f.G Eugen Bauhof�
Henry in 1997-23:Zur Union von Raumzeit und Materie würde ich allerdings sagen, Einstein hat die Raumzeit und die Materie in ein dynamisches Wechselspiel geführt, sie beeinflussen einander durch ihre gegenseitige Wirkungen - Materie krümmt die Raumzeit, die Krümmung der Raumzeit gibt der Materie ihre Bewegungsrichtung vor.
Hallo Henry,
richtig, genau das wollte ich mit dem Schlagwort "Union zwischen Raumzeit und Materie" zum Ausdruck bringen. Also, volle Übereinstimmung.
M.f.G Eugen Bauhof�
Beitrag 1997-29
-
Nun Harti,
ich würde es – weniger missverständlich – so formulieren:
Nebenbei: Der Gebrauch der Worte » Zeitdilation « und » Längenkontraktion « ist nur angebracht, wo man beobachterspezifische S i c h t e n miteinander vergleicht. Diese Worte beschreiben (wie Du intuitiv richtig erkannt, aber keineswegs überzeugend verargumentiert hast) keine Eigenschaften der Raumzeit.
Gruß, grtgrt
Harti in 1997-27:Hallo zusammen,
ich formulier die Erkenntnis aus der vektotriellen Betrachtung noch mal sprachlich:
Raumzeitlich bewegen sich die Zwillinge vom Ereignis A (Start des Reisezwillings) zum Ereignis B (Rückkehr des Reisezwillings). Diese Bewegungen beider Zwillinge sind raumzeitlich gleich. Es gibt bei dieser raumzeitlichen Betrachtung weder eine Zeitdilatation noch eine Längenkontraktion, weil es die Unterscheidung bzw. den Gegensatz zwischen Raum und Zeit nicht gibt.
Nun Harti,
ich würde es – weniger missverständlich – so formulieren:
- Die beiden Zwillinge bewegen sich von A nach B auf unterschiedlichen Wegen durch die Raumzeit.
- Je nachdem, welchen Weg sie nehmen und welch unterschiedlicher Beschleunigung sie dort ausgesetzt sind, werden sie mehr oder weniger schnell altern. Dies bewirkt, dass — wenn sie sich in B erneut treffen — ihr Alter unterschiedlich sein wird, trotzdem sie in A noch gleich alt waren.
Nebenbei: Der Gebrauch der Worte » Zeitdilation « und » Längenkontraktion « ist nur angebracht, wo man beobachterspezifische S i c h t e n miteinander vergleicht. Diese Worte beschreiben (wie Du intuitiv richtig erkannt, aber keineswegs überzeugend verargumentiert hast) keine Eigenschaften der Raumzeit.
Gruß, grtgrt
Beitrag 1997-16
-
Das ist nur rein formal richtig insofern als Minkowski auf dem durch Einstein in der SRT betrachteten Raum — den er damals noch einfach als durch Raum und Zeit aufgespannten 4-dimensionalen reelen V e k t o r r a u m sah — eine Metrik definiert hat: eben jene, die man heute die Minkoski-Metrik nennt.
Erst die ART hat dann Raum und Zeit u n t r e n n b a r miteinander verschweißt.
Bauhof in 1997-14:
die Vereinigung von Raum und Zeit zur Raumzeit hat nicht direkt Einstein, sondern Hermann Minkowski vollzogen.
Es sind nur Modell-Vorstellungen. Zeit ist eine Modellvorstellung und Raum ist eine Modellvorstellung. Minkowski hat beide Modellvorstellungen zur Modellvorstellung Raumzeit vereinigt. Warum? Weil sich mit der Raumzeit bessere nachprüfbare Vorhersagen machen lassen als mit den beiden alten Modellvorstellungen.
Das ist nur rein formal richtig insofern als Minkowski auf dem durch Einstein in der SRT betrachteten Raum — den er damals noch einfach als durch Raum und Zeit aufgespannten 4-dimensionalen reelen V e k t o r r a u m sah — eine Metrik definiert hat: eben jene, die man heute die Minkoski-Metrik nennt.
Erst die ART hat dann Raum und Zeit u n t r e n n b a r miteinander verschweißt.
Beitrag 1997-18
-
Ja, Henry, das ist so (steht aber keineswegs in Widerspruch zu meiner Aussage).
Henry in 1997-17:Gebhard, das Zitat:
" Von Stund′ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren."
von Minkowski stammt aus dem Jahre 1908 und bezieht sich auf seine vierdimensionales Analogen einer Kugel (Raum + Zeit) und auf die SRT. Die ART als Theorie der Gravitation beschreibt die Krümmung der Raumzeit, die dort mit Tensoren formal beschrieben wird.
Ja, Henry, das ist so (steht aber keineswegs in Widerspruch zu meiner Aussage).
Beitrag 1997-61
-
Ja, auch ich sehe das so.
Hallo Harti,
zunächst mal: Mannigfaltigkeiten zu kennen gehörte (als ich an der TU München studiert habe) nicht zum Stoff, den beherrschen musste, wer die Diplomprüfung für Mathematik bestehen wollte. Insofern werden auch viele Mathematiker in der Hinsicht einfach nur Laien sein.
Damit meine Erklärung des wesentlichen Unterschiedes zwischen Vektorraum und Mannigfaltigkeit verständlich ausfällt, will ich diese beiden Begriffe hier nicht definieren, sondern Dir lediglich den Unterschied zwischen ihnen erklären.
Hierzu sei angenommen, dass
Topologisch zu sein bedeutet (in diesem Fall), dass auf beiden Räumen ein durch die Minkowski-Metrik gegebener Abstandsbegriff definiert ist.
Dass wir die 4-dim Version dieser Räume betrachten — also nicht, wie etwa die Stringtheorie, gleich 10 Dimensionen voraussetzen — spielt keine Rolle für den
Unterschied zwischen » Vektorraum « einerseits und » Mannigfaltigkeit « andererseits.
Da der Raum R(SRT) ein Vektorraum ist, gilt:
Da der Raum R(ART) eine Mannigfaltigkeit ist, gilt:
Man merke sich also:
Ein Raum, der Singularitäten enthält, kann kein Vektorraum sein.
In einer Mannigfaltigkeit aber ist jedes Koordinatensystem nur l o k a l brauchbar,
d.h. nur in einer hinreichend kleinen Umgebung seines Ursprungs.
Gruß, grtgrt
Harti in 1997-59:Grtgrt in 1997-53:Raum und Zeit sind deswegen in der Argumentation sauber auseinander gehalten,
und nur deswegen kann sich die SRT leisten, als Bezugssystem keine 4-dim Mannigfaltigkeit, sondern nur einen 4-dim-Vektorraum zu haben
Hallo Grtgrt,
Muss man nicht eigentlich aus der Tatsache, dass man zwei Koordinaten verwendet, die senkrecht aufeinander stehen, schließen, dass Raum und Zeit getrennt werden ?
Die Veräumlichung der Zeit, indem man die Zeit (t) mit der Lichtgeschwindigkeit (c) multipliziert und die Zeitachse ct-Achse nennt, ändert doch daran nichts.
Ja, auch ich sehe das so.
Harti in 1997-59:
Kannst Du mir als mathematischen Laien die Begriffe 4-dim Vektorraum und 4-dim Mannigfaltigkeit und insbesondere den Unterschied zwischen beiden erklären ? Ich nehme an, es handelt sich bei einer Darstellung von Vektoren mit zwei Koordinaten, eine für die Zeit und eine für den Raum, um einen reduzierten, zweidimensionalen Vektrorraum.
Hallo Harti,
zunächst mal: Mannigfaltigkeiten zu kennen gehörte (als ich an der TU München studiert habe) nicht zum Stoff, den beherrschen musste, wer die Diplomprüfung für Mathematik bestehen wollte. Insofern werden auch viele Mathematiker in der Hinsicht einfach nur Laien sein.
Damit meine Erklärung des wesentlichen Unterschiedes zwischen Vektorraum und Mannigfaltigkeit verständlich ausfällt, will ich diese beiden Begriffe hier nicht definieren, sondern Dir lediglich den Unterschied zwischen ihnen erklären.
Hierzu sei angenommen, dass
- R(SRT) den 4-dim Raum der SRT bezeichnet, der topologischer V e k t o r r a u m ist, und
- R(ART) die 4-dim Raum der ART, der topologische M a n n i g f a l t i g k e i t ist.
Topologisch zu sein bedeutet (in diesem Fall), dass auf beiden Räumen ein durch die Minkowski-Metrik gegebener Abstandsbegriff definiert ist.
Dass wir die 4-dim Version dieser Räume betrachten — also nicht, wie etwa die Stringtheorie, gleich 10 Dimensionen voraussetzen — spielt keine Rolle für den
Unterschied zwischen » Vektorraum « einerseits und » Mannigfaltigkeit « andererseits.
Da der Raum R(SRT) ein Vektorraum ist, gilt:
- Jedes im Raum gewählte Koordinatensystem K(u), u sein Ursprung, ist brauchbar über den gesamten Raum hinweg.
- Der per Minkowski-Metrik errechnete Abstand zweier Punkte ist — seinem Wert nach — nicht abhängig vom gewählten Koordinatensystem.
Da der Raum R(ART) eine Mannigfaltigkeit ist, gilt:
- Jedes im Raum gewählte Koordinatensystem K(u), u sein Ursprung, ist nur in einer hinreichend kleinen Umgebung U von u brauchbar.
- Für sie gilt, dass mindestens eine positive reelle Zahl ε(u) existiert, so dass alle Punkte x aus R, die von u kleineren Abstand als ε(u) haben, zu U gehören und dass ferner kein Punkt aus U Singularität des Raumes ist.
- Insbesondere existiert k e i n e i n z i g e s Koordinatensystem, in das sich a l l e Punkte des Raumes einordnen lassen.
Man merke sich also:
In einer Mannigfaltigkeit aber ist jedes Koordinatensystem nur l o k a l brauchbar,
d.h. nur in einer hinreichend kleinen Umgebung seines Ursprungs.
Gruß, grtgrt
Beitrag 1985-359
-
Ja, Henry,
auch ich sehe das exakt so.
Gruß, grtgrt
Henry in 1985-358:
Man kann es auch kräftiger ausdrücken:
Es gibt keine Inertialsysteme, und die SRT ist als Spezialfall innerhalb der ART ein rein gedankliches Produkt und keinesfalls die Grundlage der ART.
Ja, Henry,
auch ich sehe das exakt so.
Gruß, grtgrt
Beitrag 2080-35
Das Blockuniversum — ein allzu ungenaues, nicht wirklich hilfreiches Modell
Hallo Henry,
es würde mich sehr wundern, wenn es eine Literaturstelle gäbe, in der Einstein selbst den Begriff "Blockuniversum" in den Mund nimmt.
Meiner Ansicht nach wird dieser Begriff nämlich nur von Leuten verwendet, die sich nicht darüber klar sind, dass die 4-dimensionale Raumzeit der ART (anders als die der SRT) eben k e i n 4-dimensionaler Vektorraum ist, sondern nur 4-dimensionale Mannigfaltigkeit, und dass man deswegen durch Fixieren eines Wertes z1 auf der Zeitachse auch nicht wirklich einen Schnitt durch die Raumzeit bekommt, der den gesamten Raum zu Zeitpunkt z1 darstellen würde.
Zeitpunkte im Sinne der ART machen stets nur l o k a l Sinn,
und so sind Zeitscheiben im Sinne des Blockuniversums gar keine wohldefinierten Konzepte.
Henry in 2080-33:
... er [Einstein] war später der Ansicht, seine Raumzeit sei real, was ihn sogar soweit brachte, ein Blockuniversum als wahrscheinlich anzunehmen.
Hallo Henry,
es würde mich sehr wundern, wenn es eine Literaturstelle gäbe, in der Einstein selbst den Begriff "Blockuniversum" in den Mund nimmt.
Meiner Ansicht nach wird dieser Begriff nämlich nur von Leuten verwendet, die sich nicht darüber klar sind, dass die 4-dimensionale Raumzeit der ART (anders als die der SRT) eben k e i n 4-dimensionaler Vektorraum ist, sondern nur 4-dimensionale Mannigfaltigkeit, und dass man deswegen durch Fixieren eines Wertes z1 auf der Zeitachse auch nicht wirklich einen Schnitt durch die Raumzeit bekommt, der den gesamten Raum zu Zeitpunkt z1 darstellen würde.
und so sind Zeitscheiben im Sinne des Blockuniversums gar keine wohldefinierten Konzepte.
Beitrag 1985-356
Beschleunigung (jeder Art) entspricht einer Krümmung der Raumzeit
Hallo Henry,
ich habe Zweifel, ob wirklich richtig ist, was Du hier sagst.
Schließlich hat Einstein selbst — z.B. mit seinem Fahrstuhl-Gedankenexperiment — immer wieder darauf hingewiesen, dass Kräfte, die beschleunigen, sich ihrer Ursache nach in keiner Weise unterscheiden lassen: Sie alle gehorchen ein und demselben mathematischen Gesetz, und so müssen sie sich doch wohl auch a l l e als Raumkrümmung deuten lassen.
Gruß, grtgrt
PS: Wo auf ein Objekt Beschleunigungskräfte unterschiedlicher Herkunft wirken, wird das Objekt sie stets als in genau e i n e Richtung ziehende Kraft wahrnehmen ganz so als hätten sie nur eine einzige Quelle und Ursache (was wirkt, ist die vektorielle Summe aller Kräfte).
Die Krümmung des Raumes im Sinne der ART scheint mir durch die Forderung definiert, dass dieser Kraftvektor überall zum Nullvektor werden muss.
Im übrigen ist es genau (und nur) diese Forderung, welche garantiert, dass jeder Punkt der Raumzeit (auch der ART) eine Umgebung hat, in der — wenn man sie klein genug wählt — die Gesetze der SRT gelten.
Henry in 1985-354:
Also nur als Ergänzung: Man kann Gravitation und Beschleunigung nicht mit denselben Gleichungen behandeln, weil Beschleunigung durch eine Kraft erzeugt wird, während die Gravitation laut ART aber keine Kraft ist, sondern die Krümmung der Raumzeit, also eine geometrische Beschreibung darstellt. Gravitation und Beschleunigung sind äquivalent, was ihre Wirkung angeht, aber nicht identisch.
Hallo Henry,
ich habe Zweifel, ob wirklich richtig ist, was Du hier sagst.
Schließlich hat Einstein selbst — z.B. mit seinem Fahrstuhl-Gedankenexperiment — immer wieder darauf hingewiesen, dass Kräfte, die beschleunigen, sich ihrer Ursache nach in keiner Weise unterscheiden lassen: Sie alle gehorchen ein und demselben mathematischen Gesetz, und so müssen sie sich doch wohl auch a l l e als Raumkrümmung deuten lassen.
Gruß, grtgrt
PS: Wo auf ein Objekt Beschleunigungskräfte unterschiedlicher Herkunft wirken, wird das Objekt sie stets als in genau e i n e Richtung ziehende Kraft wahrnehmen ganz so als hätten sie nur eine einzige Quelle und Ursache (was wirkt, ist die vektorielle Summe aller Kräfte).
Die Krümmung des Raumes im Sinne der ART scheint mir durch die Forderung definiert, dass dieser Kraftvektor überall zum Nullvektor werden muss.
Im übrigen ist es genau (und nur) diese Forderung, welche garantiert, dass jeder Punkt der Raumzeit (auch der ART) eine Umgebung hat, in der — wenn man sie klein genug wählt — die Gesetze der SRT gelten.
Beitrag 0-500
Einstein Feldgleichung wenigstens grob verstehen
Einsteins Feldgleichung
erklärt und kommentiert durch Helmut Satz
Quelle: Helmut Satz: Kosmische Dämmerung (2016), S. 181-184
erklärt und kommentiert durch Helmut Satz
Helmut Satz (2016):
Die ursprünglich von Einstein aufgestellten Gleichungen lauteten
Rμν – (1/2) R gμν = c-4 8πG Tμν ,
wobei G die Newtonsche Gravitationskonstante und c die Lichtgeschwindigkeit bezeichnet.
Die Indizes μ und ν geben Zeit und Raum an und durchlaufen somit die Werte 0 (Zeit) und 1,2,3 (Raum).
Der sog. metrische Tensor gμν definiert die Raumzeit ohne Gravitation, d.h. den flachen Minkowski-Raum. R ist ein Skalenfaktor (sog. Ricci-Krümmungsskalar).
Der sog. Energie-Impuls-Tensor Tμν beschreibt den Rauminhalt. d.h. die Energiedichte ρ im Raum sowie den daraus resultierenden Druck p.
Der sog. (Ricci-) Krümmungs-Tensor Rμν schließlich beschreibt die durch den Rauminhalt erzeugte Krümmung von Raum und Zeit.
Alle Tensoren der Gleichung sind symmetrisch (so dass man statt 16 nur 10 Gleichungen hat).
Eine Aussage dieser Gleichungen ist, dass sich die Größe des Weltraums aufgrund seines Inhalts verändern kann.
Das Maß dieser Änderung ist der schon erwähnte Skalenfaktor R = a(t) — er skaliert die Abstände im Raum und somit die Raumgröße.
Für ihn ergeben sich aus Einsteins Gleichung zwei Beziehungen, die als erster 1922 der russische Physiker Alexander Friedmann hergeleitet hat. Die erste
H2 = (( da/dt )/a )2 = ( 8πG/3 )ρ – k/a2 ,
bestimmt die Geschwindigkeit v = da/dt, mit der sich die Skala verändert ( H ist somit das, was man heute den sog. Hubble-Parameter nennt).
ρ ist die Energiedichte im Raum, und
k spezifiziert die Raumstruktur: Für flachen Raum ist k = 0, für sphärischen k = 1 unf für hyperbolischen k = –1.
Friedmanns zweite Gleichung bestimmt die Veränderung der Skalengeschwindigkeit (da/dt)dt = a'' = v' und sagt:
a''/a = –( 4/3 )πG ( ρ + 3p ) ,
Dieser zweite von Friedmann abgeleitete Zusammenhang zeigt, dass Einsteins Wunsch nach einem statischen Universum durch seine Gleichungen in ihrer Urform (s.o.) nicht erfüllbar ist, denn selbst wenn man bei sphärischer Krümmung des Raumes (k = 1) Friedmanns zweite Gleichung zu irgend einem Zeitpunkt da/dt = 0 zulassen würde, zeigt die Gleichung, dass sich das rasch wieder ändern muss.
Einstein sah nun aber, dass die mathematische Struktur seiner Gleichungen eine Abänderung erlaubt: Man kann der linken Seite einen additiven Term hinzufügen, so dass die Gleichung dann lautet:
Rμν – (1/2) R gμν + Λμν = c-4 8πG Tμν ,
wo Λ eine universelle, positive, räumlich und zeitlich konstante Größe ist (eine sog. kosmologische Konstante).
Sie hat zur Folge, dass sich zur rechten Seite beider Gleichungen von Friedmann die Zahl Λ/3 addiert.
Damit schien Einsteins Wunsch nach einem statischen Universum zunächst erfüllbar: Bei sphärischer Raumkrümmung nämlich (k = 1) gibt es gemeinsame Werte Λ, p und ρ, welche die erste und die zweite Ableitung von a nach der Zeit zu Null machen.
Schon bald aber wurde klar, dass jede noch so kleine zeitliche Schwankung der Energiedichte das statische Universum instabil machen würde in dem Sinne, dass der Raum dann sofort zu expandieren oder zu kontrahieren beginnen würde.
Hinzu kam Hubbles Entdeckung, des expandierenden Weltalls: Das Universum ist tatsächlich nicht statisch.
Einstein soll deswegen die Einführung seiner "kosmologischen" Konstanten als "größte Eselei seines Lebens" bezeichnet haben.
Heute denkt man eher, dass seine Konstante vielleicht doch Sinn macht:
Mit Λ = 0 nämlich kann man zwar ein expandierendes Universum erhalten, aber nur eines, bei der die Expansionsrate mit der Zeit abnimmt.
Mitte der 1990-er Jahre gesammelte Supernova-Daten zeigen nun aber, dass die Expansionsrate sich mit der Zeit vergrößert statt verkleinert, was ein positives, hinreichend großes Λ erfordert.
Erst damit lassen sich die neueren Vorstellungen von Multiversum und Iflation problemlos in den gegebenen Rahmen einfügen.
Man schreibt den Λ-Term dann auf die rechte Seite der Gleichung, um zu betonen, dass die Entwicklung der Krümmung des Raumes
- nicht nur durch die von den Objekten im Raum kommende Energiedichte T bestimmt ist,
- sondern eben auch durch ein dem Raum selbst innewohnendes, konstantes Feld Λ der Gravitation entgegen wirkender Energie.
Mit Hilfe der genannten Supernova-Beobachtungsdaten kann man die Größe von Λ dann sogar errechnen.
Und so gibt man Einsteins Feldgleichung heute die Form
Rμν – (1/2) R gμν = c-4 8πG Tμν – Λμν ,
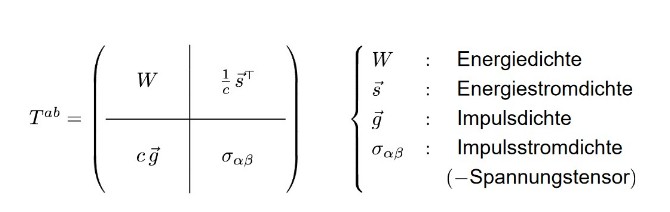
Der Energie-Impuls-Tensor
Beitrag 0-468
Der Energie-Erhaltungssatz — hier genau formuliert
Zum Energie-Erhaltungssatz
Quelle: Thomas und Brigitte Görnitz: Von der Quantenphysik zum Bewusstsein, Springer 2015, S. 517 und 518
Thomas Görnitz (2015):
Der Satz von der » Erhaltung der Energie « wurde
- vom Arzt und Physiker Robert Mayer (1814-1878) entdeckt
- und später von Hermann von Helmholz (1821-1894) endgültig ausformuliert.
Er wird oft so verstanden, dass die Energie in einem abgeschlossenen System — worunter man eines versteht, welches mit seiner Umgebung keine Energie austauscht — unverändert bleibt.
Dies gilt aber nur, solange das System sein Volumen nicht verändert.
Thomas Görnitz (2015):
Seit Einsteins Relativitätstheorie wissen Kosmologen, dass es für realistische kosmologische Modelle keinen Energie-Erhaltungssatz geben kann.
Man kann ihn zwar für den Minkowski-Raum herleiten, der aber hat mit der kosmologischen Realität nichts zu tun. Er ist ein Raummodell, das den Raum als flach und in jeder Dimension als zwingend unendlich weit darstellt. Quantenfeldtheorie und Elementarteilchenphysik werden dennoch in diesem Modell abgehandelt — unter der Annahme, das der Energie-Erhaltungssatz Gültigkeit habe.
Beitrag 0-12
Wie sich Energie definiert
Was ist Energie?
In Abänderung dessen, was Hans-m in 2132-11 schreibt, würde ich definieren:
Energie ist dort, wo Zustand sich verändert oder Kraft auf Gegenkraft trifft.
Mit anderen Worten:
Energie ist die Möglichkeit, auf Zustandsveränderung hinzuwirken.
Energie ist z.B. dort, wo
Schon das erste Beispiel ist ein sehr interessantes, denn wo zwei Objekte — ein Objekt X und sein Beobachter B — sich relativ zueinander gleichförmig bewegen, wird die entsprechende kinetische Energie
Schon dieses einfache Beispiel also zeigt:
Energie lässt sich stets nur beobachterspezifisch quantifizieren.
In Abänderung dessen, was Hans-m in 2132-11 schreibt, würde ich definieren:
Mit anderen Worten:
Energie ist z.B. dort, wo
- sich etwas bewegt (kinetische Energie),
- wo sich Kraftpotential aufbaut oder aufgebaut hat,
- wo Kohlenstoff- und Sauerstoffatom eine Bindung eingehen (chemische Energie).
Schon das erste Beispiel ist ein sehr interessantes, denn wo zwei Objekte — ein Objekt X und sein Beobachter B — sich relativ zueinander gleichförmig bewegen, wird die entsprechende kinetische Energie
- aus Sicht von B stets nur X zuzuschreiben sein
- und zudem noch proportional zur Masse von X sein.
Schon dieses einfache Beispiel also zeigt:
Beitrag 0-211
Kosmologische Konstante und die Energie des Vakuums
Die kosmologische Konstante
Im November 1915 publizierte Einstein die erste von ihm selbst als fertig erachtete Fassung seiner Feldgleichung der Allgemeinen Relativitätstheorie (ART).
Wie ihm erst ein Jahr später bewusst wurde, hatte er darin eine Integrationskonstante stillschweigend weggelassen, d.h. angenommen, ihr physikalisch einzig sinnvoller Wert sei Null.
Diese Größe — heute durch den griechischen großen Buchstaben Λ bezeichnet und kosmologische Konstante genannt — hat sich inzwischen als wichtiger Parameter unseres Universums herausgestellt. Physikalisch lässt sie sich auffassen
Jeder positive Wert dieser Konstanten resultiert in beschleunigter Raumexpansion — und seit 1998 weiß man, dass viele unserer astronomischen Beobachtungen auf eben sie hindeuten.
Ist H der Hubbleparameter und setzt man ΩΛ = Λ/(3H2), so zeigen Einsteins Gleichungen, dass die Expansion des Raumes sich beschleunigt, solange ΩΛ größer als die halbe Massendichte Ωm/2 ist.
Die beste Übereinstimmung mit heute vorhandenen Beobachtungsdaten ergibt sich, wenn man Ωm = 0,3 und ΩΛ = 0,7 annimmt, was ganz deutlich die Bedingungen für beschleunigte Expansion des Raumes erfüllt.
Verletzt das Vakuum den Energie-Erhaltungssatz?
Dass physikalische Größen wie Energie und Impuls in einem geschlossenen System weder verschwinden, noch zusätzlich auftauchen können, ist ein ganz zentraler Grundsatz der klassischen Physik und war wichtiger Ausgangspunkt von Einsteins Entwicklung der ART.
Für expandierende Raumzeiten allerdings, lassen sich solche Erhaltungssätze bisher n i c h t begründen.
Paul Davies und Edward R. Harrison — beides Kosmologen — argumentierten schon in den 80-er Jahren, dass man die Expansion des Raumes als Energiequelle sehen müsse, ohne dass klar sei, woher jene Energie kommt.
Und auf der Frühjahrstagung 2015 der Deutschen Physikalischen Gesellschaft wies Gerhard Schäfer (Universität Jena) darauf hin: "Das Thema Energie in der relativistischen Kosmologie ist eine Katastrophe."
Quelle:
Rüdiger Vaas: Jenseits von Einsteins Universum (2016),
S. 188 bzw. 191-192.
Lies auch: Das Rätsel der kosmischen Vakuumenergiedichte und die beschleunigte Expansion des Universums
Lies ferner: Dis komologische Konstante
Im November 1915 publizierte Einstein die erste von ihm selbst als fertig erachtete Fassung seiner Feldgleichung der Allgemeinen Relativitätstheorie (ART).
Wie ihm erst ein Jahr später bewusst wurde, hatte er darin eine Integrationskonstante stillschweigend weggelassen, d.h. angenommen, ihr physikalisch einzig sinnvoller Wert sei Null.
Diese Größe — heute durch den griechischen großen Buchstaben Λ bezeichnet und kosmologische Konstante genannt — hat sich inzwischen als wichtiger Parameter unseres Universums herausgestellt. Physikalisch lässt sie sich auffassen
- entweder als eine Eigenschaft der Raum-Zeit-Geometrie
- oder als Energiedichte des Vakuums.
Jeder positive Wert dieser Konstanten resultiert in beschleunigter Raumexpansion — und seit 1998 weiß man, dass viele unserer astronomischen Beobachtungen auf eben sie hindeuten.
Interessant ist, dass Einstein selbst, diese Konstante zwar zunächst doch berücksichtigt hat, dies aber später — 1931, George Gamov gegenüber — als seine größte Eselei bezeichnete (da sie seinem Glauben an ein statisches Universum widersprach).
Dieses Beispiel zeigt sehr schön, wie wichtig es zu sein scheint, den Aussagen der Mathematik zu vertrauen — also nicht zu glauben, dass durch sie aufgedeckte Möglichkeiten nicht doch etwas mit physikalischer Realität zu tun haben könnten.
|
Heute gilt Λ als die einfachste Erklärung für die Triebkraft der kosmischen Expansion: für das, was man Dunkle Energie nennt (oder auch negative Gravitation).
Man kann es auch so sagen: Dunkle Energie ist ein Konzept, welches Einsteins kosmologische Konstante verallgemeinert zu einer zeitlich variablen Größe.
Der aus kosmologischen Beobachtungen ermittelte derzeitige Wert der Zahl ist um etwa 120 Größenordnungen kleiner, als der durch die Quantenfeldtheorie vorhergesagte. Irgendwas also hat man bisher noch nicht verstanden. Man könnte aber auch auf die Idee kommen, diese Diskrepanz als Anzeichen dafür zu deuten, dass Gravitation — als durch die Quantentheorie bisher vernachlässigte Kraft — selbst im Vakuum noch eine recht große Rolle spielt.
Ist H der Hubbleparameter und setzt man ΩΛ = Λ/(3H2), so zeigen Einsteins Gleichungen, dass die Expansion des Raumes sich beschleunigt, solange ΩΛ größer als die halbe Massendichte Ωm/2 ist.
Die beste Übereinstimmung mit heute vorhandenen Beobachtungsdaten ergibt sich, wenn man Ωm = 0,3 und ΩΛ = 0,7 annimmt, was ganz deutlich die Bedingungen für beschleunigte Expansion des Raumes erfüllt.
Dass physikalische Größen wie Energie und Impuls in einem geschlossenen System weder verschwinden, noch zusätzlich auftauchen können, ist ein ganz zentraler Grundsatz der klassischen Physik und war wichtiger Ausgangspunkt von Einsteins Entwicklung der ART.
Für expandierende Raumzeiten allerdings, lassen sich solche Erhaltungssätze bisher n i c h t begründen.
Paul Davies und Edward R. Harrison — beides Kosmologen — argumentierten schon in den 80-er Jahren, dass man die Expansion des Raumes als Energiequelle sehen müsse, ohne dass klar sei, woher jene Energie kommt.
Und auf der Frühjahrstagung 2015 der Deutschen Physikalischen Gesellschaft wies Gerhard Schäfer (Universität Jena) darauf hin: "Das Thema Energie in der relativistischen Kosmologie ist eine Katastrophe."
Lies auch: Das Rätsel der kosmischen Vakuumenergiedichte und die beschleunigte Expansion des Universums
Lies ferner: Dis komologische Konstante
Beitrag 0-124
Wie Einstein entdeckt hat, dass auch Masse einfach nur Energie ist
Begründung der Formel E = m c2
Quelle:
Hans Christian von Baeyer: Das informative Universum, Verlag C.H.Beck 2005, S 237.
Der Physiker von Baeyer schreibt:
Als Einstein seine neuen Gesetze der Mechanik aufstellte, fand er, dass sich das Axiom von der Erhaltung der Energie in sich abgeschlossener Systeme nur dann aufrecht erhalten lässt, wenn man die unerwartete Formel
E = m c2
annimmt ( siehe auch wie man das nachrechnet ).
Sowohl die Spezielle wie auch die Allgemeine Relativitätstheorie führten somit überraschenderweise zu einer Verallgemeinerung der universellen Gesetze von Rudolf Clausius (dem Entdecker des zweiten Hauptsatzes der Thermodynamik). Ausgedrückt in der Sprache der modernen Physik lauten sie:
Die Energie des Universums – einschließlich der Ruheenergie massiver Körper – ist konstant.
( Aber macht, das zu sagen denn überhaupt Sinn?
Sicher nicht für einzelne Universen, wohl aber für den Kosmos insgesamt. )
Die Entropie des Universums – einschließlich der Schwarzer Löcher – nimmt niemals ab.
Beitrag 0-217
Gravitation dehnt Zeit und Licht
Formeln für
Gravitative Rotverschiebung und entsprechende Dehnung der Zeit
Im Schwerefeld vergrößert sich die Wellenlänge von Licht, und alle Uhren gehen dort langsamer.
So sagt Einsteins Theorie, und 1959 von Pound und Rebka erstmals vorgenommene Messungen haben es bestätigt:
Gravitative Rotverschiebung führt zu einem optischen Dopplereffekt, der gegenüber der Ruhe-Wellenlänge λ0 zu einer Wellenlängen-Änderung
Δλ = mEGL/2c2rR2
führt. Hierin bezeichnen mE und rE Masse und Radius der Erde, L die Höhendifferenz, die das Licht ausgehend vom Erdboden hin zum höher gelegenen Detektor überwinden muss, G Newtons Gravitationskonstante, und c die Lichtgeschwindigkeit.
Beim Experiment von Pound und Rebka betrug der Höhenunterschied 22,5 Meter, so dass die vorhergesagte Rotverschiebung einer Eisen-57-Spektrallinie Δλ0 = 4,9 • 10-15 betrug — im Einklang mit Messungen, die diesen Wert 1959 mit einer Ungenauigkeit von 10% — bestätigten.
1964 gelang es Pound und Snider, ihn mit einer Ungenauigkeit von unter 1% zu messen.
Da die Zeit über eine Frequenz ν definierbar ist und dann ν = c/λ gilt, lässt sich aus der gravitativen Rotverschiebung auf die Zeitdehnung Δt schließen, die für eine Uhr eintritt, welche in der Entfernung r vom Schwerpunkt einer Masse m eines Körpers K vom Radius rS = 2Gm/c2 retaltiv zur Zeit t0 eines Beobachters fern vom Gravitationsfeld. Man hat
Δt(r) = Δt0 ( 1 – rS/r )1/2
Die Größe rS ist übrigens der sog. Schwarzschild-Radius des Körpers K.
Befindet sich eine Raumsonde Δt = 1 Jahr lang r = 35 km entfernt vom Rand eines Schwarzen Lochs mit 10 Sonnenmassen, so vergehen während dessen für weit entfernt außerhalb des Schwerefeldes weilende Beobachter Δt0 = 2,5 Jahre .
Für eine kreisförmige Umlaufbahn muss der Orbitalradius größer als das 1,5-fache von rS sein.
Die gravitative Zeitdehnung für eine Uhr im Orbit ist dann Δt(r) = Δt0 ( 1 – 3rS/2r )1/2 .
Quelle: Rüdiger Vaas: Jenseits von Einsteins Universum (2016), S. 302-303.
Gravitative Rotverschiebung und entsprechende Dehnung der Zeit
Im Schwerefeld vergrößert sich die Wellenlänge von Licht, und alle Uhren gehen dort langsamer.
So sagt Einsteins Theorie, und 1959 von Pound und Rebka erstmals vorgenommene Messungen haben es bestätigt:
Gravitative Rotverschiebung führt zu einem optischen Dopplereffekt, der gegenüber der Ruhe-Wellenlänge λ0 zu einer Wellenlängen-Änderung
führt. Hierin bezeichnen mE und rE Masse und Radius der Erde, L die Höhendifferenz, die das Licht ausgehend vom Erdboden hin zum höher gelegenen Detektor überwinden muss, G Newtons Gravitationskonstante, und c die Lichtgeschwindigkeit.
Beim Experiment von Pound und Rebka betrug der Höhenunterschied 22,5 Meter, so dass die vorhergesagte Rotverschiebung einer Eisen-57-Spektrallinie Δλ0 = 4,9 • 10-15 betrug — im Einklang mit Messungen, die diesen Wert 1959 mit einer Ungenauigkeit von 10% — bestätigten.
Da die Zeit über eine Frequenz ν definierbar ist und dann ν = c/λ gilt, lässt sich aus der gravitativen Rotverschiebung auf die Zeitdehnung Δt schließen, die für eine Uhr eintritt, welche in der Entfernung r vom Schwerpunkt einer Masse m eines Körpers K vom Radius rS = 2Gm/c2 retaltiv zur Zeit t0 eines Beobachters fern vom Gravitationsfeld. Man hat
Die Größe rS ist übrigens der sog. Schwarzschild-Radius des Körpers K.
Befindet sich eine Raumsonde Δt = 1 Jahr lang r = 35 km entfernt vom Rand eines Schwarzen Lochs mit 10 Sonnenmassen, so vergehen während dessen für weit entfernt außerhalb des Schwerefeldes weilende Beobachter Δt0 = 2,5 Jahre .
Für eine kreisförmige Umlaufbahn muss der Orbitalradius größer als das 1,5-fache von rS sein.
Die gravitative Zeitdehnung für eine Uhr im Orbit ist dann Δt(r) = Δt0 ( 1 – 3rS/2r )1/2 .
Quelle: Rüdiger Vaas: Jenseits von Einsteins Universum (2016), S. 302-303.
Beitrag 2058-1
Wie relativ ist Energie?
Wie man der kosmischen Rotverschiebung wegen erkennt, haben Photonen, die in einer fernen Galaxis erzeugt werden, aus Sicht ihrer Quelle kürzere Wellenlänge (also höhere Frequenz und deswegen höhere Energie) als aus unserer Sicht.
FRAGE also:
Wie man der kosmischen Rotverschiebung wegen erkennt, haben Photonen, die in einer fernen Galaxis erzeugt werden, aus Sicht ihrer Quelle kürzere Wellenlänge (also höhere Frequenz und deswegen höhere Energie) als aus unserer Sicht.
FRAGE also:
- Wohin ist ein Teil ihrer Energie verschwunden?
- Geht solcher Schwund auch nur gequantelt vor sich, oder müssen wir Energie ebenso relativ sehen wie Raum und Zeit?
Beitrag 2058-17
Energie ist relativ (wie Zeit und Raum)
Hallo zusammen,
die Frage des Threads lautet: ist Energie relativ.
Meine Antwort: ja, die Energie die wir wahrnehmen ist abhängig vom Bezugssystem des Beobachters. Dafür habe ich Beispiele angeführt die bisher keiner widerlegen konnte. Ich könnte noch weitere Beispiele anführen, erspare mir das aber an dieser Stelle, da es hier scheinbar um etwas anderes geht.
Nur so viel – die Vorstellung, Licht könnte gedehnt oder gestaucht werden, oder sich auf eine größere Entfernung verteilen, halte ich für eine falsche Vorstellung.
Beispiel:
Eine Rakete A sendet ein blaues Lichtsignal aus. Ein in der Nähe befindliches zur ersten RaketeA fortbewegende Rakete B empfängt dieses Signal rotverschoben, also mit weniger Energie. Eine weiter entfernte Rakete C, die zur ersten Rakete A ruht, empfängt das Lichtsignal als Blau, also mit höherer Energie wie Rakete B, obwohl das Licht über eine "längere Strecke", wie du es Henry ausdrückst, verteilt ist.
Mit Energieverlust hat das nichts zu tun und habe ich auch nie behauptet.
mfg okotombrok�
die Frage des Threads lautet: ist Energie relativ.
Meine Antwort: ja, die Energie die wir wahrnehmen ist abhängig vom Bezugssystem des Beobachters. Dafür habe ich Beispiele angeführt die bisher keiner widerlegen konnte. Ich könnte noch weitere Beispiele anführen, erspare mir das aber an dieser Stelle, da es hier scheinbar um etwas anderes geht.
Nur so viel – die Vorstellung, Licht könnte gedehnt oder gestaucht werden, oder sich auf eine größere Entfernung verteilen, halte ich für eine falsche Vorstellung.
Beispiel:
Eine Rakete A sendet ein blaues Lichtsignal aus. Ein in der Nähe befindliches zur ersten RaketeA fortbewegende Rakete B empfängt dieses Signal rotverschoben, also mit weniger Energie. Eine weiter entfernte Rakete C, die zur ersten Rakete A ruht, empfängt das Lichtsignal als Blau, also mit höherer Energie wie Rakete B, obwohl das Licht über eine "längere Strecke", wie du es Henry ausdrückst, verteilt ist.
Mit Energieverlust hat das nichts zu tun und habe ich auch nie behauptet.
mfg okotombrok�
Beitrag 2058-20
-
Hallo Okotombrok,
das Beispiel, das Du in Beitrag 2058-3 gegeben hast — die Lage-Energie eines Steines — beweist m.E. keineswegs, dass die Gesamtenergie eines physikalischen Objektes relativ ist:
Es zeigt lediglich, dass der Teil seiner Energie, der aus Sicht des Beobachters in bestimmter F o r m vorliegt, seiner Menge nach relativ ist.
Dennoch hast du natürlich recht: Energie ist relativ, was alleine schon daraus folgt, dass die Energie, die ein Objekt darstellt, impulsabhängig ist, sein Impuls aber geschwindigkeitsabhängig, und Geschwindigkeit stets nur als relative Geschwindigkeit existiert (vom der Geschwindigkeit, mit der sich Licht ausbreitet, mal abgesehen).
Gruß, grtgrt
PS: Der Seite http://www.energievergleich.de/energie-lexikon/mech... entnehme ich:
Jeder Körper, an dem Arbeit verrichtet worden ist, besitzt mechanische Energie, die sich in drei Formen manifestiert. Diese sind:
Darüber hinaus können Teile der Energie eines Körpers vorliegen in Form von
Okotombrok in 2058-17:
Die Frage des Threads lautet: Ist Energie relativ?
Meine Antwort: ja, die Energie die wir wahrnehmen ist abhängig vom Bezugssystem des Beobachters.
Dafür habe ich Beispiele angeführt die bisher keiner widerlegen konnte. Ich könnte noch weitere Beispiele anführen, erspare mir das aber an dieser Stelle, ...
Hallo Okotombrok,
das Beispiel, das Du in Beitrag 2058-3 gegeben hast — die Lage-Energie eines Steines — beweist m.E. keineswegs, dass die Gesamtenergie eines physikalischen Objektes relativ ist:
Dennoch hast du natürlich recht: Energie ist relativ, was alleine schon daraus folgt, dass die Energie, die ein Objekt darstellt, impulsabhängig ist, sein Impuls aber geschwindigkeitsabhängig, und Geschwindigkeit stets nur als relative Geschwindigkeit existiert (vom der Geschwindigkeit, mit der sich Licht ausbreitet, mal abgesehen).
Gruß, grtgrt
PS: Der Seite http://www.energievergleich.de/energie-lexikon/mech... entnehme ich:
Jeder Körper, an dem Arbeit verrichtet worden ist, besitzt mechanische Energie, die sich in drei Formen manifestiert. Diese sind:
- kinetische Energie (Bewegungsenergie),
- potentielle Energie, also der Lageenergie, die sich für jeden Körper aus seiner Position im Schwerefeld ergibt,
- Spannenergie, die aus der elastischen Verformung eines Körpers resultiert.
Darüber hinaus können Teile der Energie eines Körpers vorliegen in Form von
- Wärmeenergie,
- Druck-Volumenenergie,
- Strahlenenergie,
- Kernenergie,
- elektrischer Energie.
Beitrag 2058-21
Die einzig sinnvolle Erklärung für den (nur scheinbaren) Energieverlust
So, da bin ich wieder!
Ich fange noch mal an. Gebhard stellte die Frage, ob die kosmische Rotverschiebung mit einem Energieverlust einhergeht, ob dieser Schwund gequantelt ist.
Mein Antwort darauf: Energie ist immer gequantelt ist (siehe Planck und Einstein), es gibt aber keinen Energieverlust, sondern allenfalls Umwandlung von Energie von einer in eine andere Form.
Energie ist eine Erhaltungsgröße und kann nicht "schwinden".
Die kosmische Rotverschiebung ist nicht mit einem Energieschwund verbunden. Energie ist – wie gesagt - eine Erhaltungsgröße, kann also per se nicht "verlustig gehen".
Die Frage, wo sie denn geblieben wäre, wenn sie denn schwinden würde, ist also nicht sinnvoll, Energie kann in verschiedene Formen umgewandelt werden, wo aber ist die "Energieform", in die sich das Licht gewandelt haben sollte?
Licht verliert keine Energie, wenn es sich durch den Raum bewegt, das ist ein gesichertes Faktum, es sei denn, es tritt in Wechselwirkung mit Materie (Gas, Staub) oder es wird durch Gravitationspotentiale gelenkt, beides lässt sich aber aus der beobachteten Rotverschiebung herausrechnen.
Was bleibt, ist die Rotverschiebung an sich, und die ist auf die Expansion des Raumes zurückzuführen, was heißt, die größeren Wellenlängen sind genau darauf zurück zu führen, die Energie ist auf ein größeres Volumen verteilt und nicht "verschwunden". Als Beispiel denke man z. B. an die kosmische Hintergrundstrahlung : Die Energie der gesamten kosmischen Hintergrundstrahlung war etwa vierhunderttausend Jahre nach dem großen Knall (oder dem wie auch immer gearteten Anfang) auf ein Volumen mit dem Radius von eben vierhunderttausend Lichtjahren verteilt, heute entspricht das Volumen einem Radius von 13,7 Milliarden Lichtjahren, das genau und sonst nichts ist der Grund, warum die kosmische Hintergrundstrahlung heute eine Temperatur von rund 2,7 Grad Kelvin hat mit der entsprechenden Wellenlänge im Mikrowellenbereich.
Weiter ist die Bewegung der Galaxien aufgrund der Expansion des Raumes keine Relativbewegung. Die Rotverschiebung ist von jedem Punkt des Kosmos dieselbe, es handelt sich nicht um eine Bewegung innerhalb der Raumzeit, sondern um eine Bewegung der Raumzeit selbst, und diese Bewegung wäre allenfalls von "außen" betrachtet eine Relativbewegung, für Objekte innerhalb des Kosmos ist sie absolut.
Was ist mit der Rotverschiebung der Galaxien aufgrund ihrer Eigenbewegung? Diese Bewegungen sind natürliche relativ, also nur in Bezug zueinander zu bestimmen. Was heißt das für die Rotverschiebung?
Auch für dieses Licht gilt der Satz der Energieerhaltung.
Licht, das von einem Stern zu uns kommt, ist je nachdem, ob der Stern sich uns nähert oder sich von uns entfernt, blau- oder rotverschoben. Was bedeutet das für die Energie des Lichtes, das uns erreicht? Wenn wir außer Acht lassen, dass das Licht z. B. das Gravitationsfeld des jeweiligen Sternes verlassen muss und aufgrund DESSEN eine Rotverschiebung erfährt, haben wir es auch hier nicht mit einem Energieverlust zu tun. An Doppelsternensystemen kann man nachweisen, dass auch das Licht des Begleiters leicht rot- oder blauverschoben ist, je nach dem, ob er sich in Bezug auf uns zu uns hin oder zu uns weg bewegt, während er sein Muttergestirn umkreist. Da nicht anzunehmen ist, dass sich die Energie des Lichtes ändert, je nachdem, wo sich der Begleiterstern auf seiner Bahn in Bezug auf uns befindet, ist es also auf die größer oder kleinere Entfernung zurück zu führen, mit welcher Wellenlänge das Licht uns erreicht, es kann nicht an einem "Energieverlust" liegen.
Das Beispiel mit der Lichtquelle (Laserkanone) hat einen entscheidenden Haken: Man kann Licht selbst nicht beobachten! Was heißt das? Wir müssen auch am Entstehungsort des Laserstrahles einen Detektor benutzen,um das Licht zu registrieren (das wir Laserlicht z. B. grün sehen, liegt an der Atmosphäre, im Vakuum sehen wir nichts!). Wenn wir also den Laserstrahl verfolgen wollen, müssen wir in bestimmten Entfernungen im Raum Detektoren installieren, sinnvoller Weise Spiegel, anhand des so reflektierten Strahles würden wir aber feststellen, das sich die Detektoren aufgrund unserer Eigenbewegung von uns entfernen, was eine Rotverschiebung des Strahles zur Folge hätte.
Wir sehen also das Licht, wenn wir es registrieren, auf jeden Fall rotverschoben, egal, ob wir es als ursprünglich von einem entfernten Objekt kommend messen, oder ob wir das Licht erst von einer "heimischen" Quelle aussenden.
Es liegt an der Bewegung, dass das Licht rot- oder blauverschoben wird, das ist richtig, aber es hat nichts mit einem Energieverlust zu tun, Energie ist – ich muss mich wiederholen – eine Erhaltungsgröße, wir müssen also erklären, warum es eine Rot- oder Blauverschiebung gibt, und es gibt keine andere Erklärung als die sich vergrößernde bzw. verkleinernde Wegstrecke, die das Licht aufgrund der Bewegung zurückleben muss; und das liegt an der Konstanz der Lichtgeschwindigkeit, deshalb die Verschiebung.�
Okotombrok in 2058-17:Hallo zusammen,
die Frage des Threads lautet: ist Energie relativ.
Meine Antwort: ja, die Energie die wir wahrnehmen ist abhängig vom Bezugssystem des Beobachters. Dafür habe ich Beispiele angeführt die bisher keiner widerlegen konnte. Ich könnte noch weitere Beispiele anführen, erspare mir das aber an dieser Stelle, da es hier scheinbar um etwas anderes geht.
Nur so viel – die Vorstellung, Licht könnte gedehnt oder gestaucht werden, oder sich auf eine größere Entfernung verteilen, halte ich für eine falsche Vorstellung.
Beispiel:
Eine Rakete A sendet ein blaues Lichtsignal aus. Ein in der Nähe befindliches zur ersten RaketeA fortbewegende Rakete B empfängt dieses Signal rotverschoben, also mit weniger Energie. Eine weiter entfernte Rakete C, die zur ersten Rakete A ruht, empfängt das Lichtsignal als Blau, also mit höherer Energie wie Rakete B, obwohl das Licht über eine "längere Strecke", wie du es Henry ausdrückst, verteilt ist.
Mit Energieverlust hat das nichts zu tun und habe ich auch nie behauptet.
mfg okotombrok
So, da bin ich wieder!
Ich fange noch mal an. Gebhard stellte die Frage, ob die kosmische Rotverschiebung mit einem Energieverlust einhergeht, ob dieser Schwund gequantelt ist.
Mein Antwort darauf: Energie ist immer gequantelt ist (siehe Planck und Einstein), es gibt aber keinen Energieverlust, sondern allenfalls Umwandlung von Energie von einer in eine andere Form.
Energie ist eine Erhaltungsgröße und kann nicht "schwinden".
Die kosmische Rotverschiebung ist nicht mit einem Energieschwund verbunden. Energie ist – wie gesagt - eine Erhaltungsgröße, kann also per se nicht "verlustig gehen".
Die Frage, wo sie denn geblieben wäre, wenn sie denn schwinden würde, ist also nicht sinnvoll, Energie kann in verschiedene Formen umgewandelt werden, wo aber ist die "Energieform", in die sich das Licht gewandelt haben sollte?
Licht verliert keine Energie, wenn es sich durch den Raum bewegt, das ist ein gesichertes Faktum, es sei denn, es tritt in Wechselwirkung mit Materie (Gas, Staub) oder es wird durch Gravitationspotentiale gelenkt, beides lässt sich aber aus der beobachteten Rotverschiebung herausrechnen.
Was bleibt, ist die Rotverschiebung an sich, und die ist auf die Expansion des Raumes zurückzuführen, was heißt, die größeren Wellenlängen sind genau darauf zurück zu führen, die Energie ist auf ein größeres Volumen verteilt und nicht "verschwunden". Als Beispiel denke man z. B. an die kosmische Hintergrundstrahlung : Die Energie der gesamten kosmischen Hintergrundstrahlung war etwa vierhunderttausend Jahre nach dem großen Knall (oder dem wie auch immer gearteten Anfang) auf ein Volumen mit dem Radius von eben vierhunderttausend Lichtjahren verteilt, heute entspricht das Volumen einem Radius von 13,7 Milliarden Lichtjahren, das genau und sonst nichts ist der Grund, warum die kosmische Hintergrundstrahlung heute eine Temperatur von rund 2,7 Grad Kelvin hat mit der entsprechenden Wellenlänge im Mikrowellenbereich.
Weiter ist die Bewegung der Galaxien aufgrund der Expansion des Raumes keine Relativbewegung. Die Rotverschiebung ist von jedem Punkt des Kosmos dieselbe, es handelt sich nicht um eine Bewegung innerhalb der Raumzeit, sondern um eine Bewegung der Raumzeit selbst, und diese Bewegung wäre allenfalls von "außen" betrachtet eine Relativbewegung, für Objekte innerhalb des Kosmos ist sie absolut.
Was ist mit der Rotverschiebung der Galaxien aufgrund ihrer Eigenbewegung? Diese Bewegungen sind natürliche relativ, also nur in Bezug zueinander zu bestimmen. Was heißt das für die Rotverschiebung?
Auch für dieses Licht gilt der Satz der Energieerhaltung.
Licht, das von einem Stern zu uns kommt, ist je nachdem, ob der Stern sich uns nähert oder sich von uns entfernt, blau- oder rotverschoben. Was bedeutet das für die Energie des Lichtes, das uns erreicht? Wenn wir außer Acht lassen, dass das Licht z. B. das Gravitationsfeld des jeweiligen Sternes verlassen muss und aufgrund DESSEN eine Rotverschiebung erfährt, haben wir es auch hier nicht mit einem Energieverlust zu tun. An Doppelsternensystemen kann man nachweisen, dass auch das Licht des Begleiters leicht rot- oder blauverschoben ist, je nach dem, ob er sich in Bezug auf uns zu uns hin oder zu uns weg bewegt, während er sein Muttergestirn umkreist. Da nicht anzunehmen ist, dass sich die Energie des Lichtes ändert, je nachdem, wo sich der Begleiterstern auf seiner Bahn in Bezug auf uns befindet, ist es also auf die größer oder kleinere Entfernung zurück zu führen, mit welcher Wellenlänge das Licht uns erreicht, es kann nicht an einem "Energieverlust" liegen.
Das Beispiel mit der Lichtquelle (Laserkanone) hat einen entscheidenden Haken: Man kann Licht selbst nicht beobachten! Was heißt das? Wir müssen auch am Entstehungsort des Laserstrahles einen Detektor benutzen,um das Licht zu registrieren (das wir Laserlicht z. B. grün sehen, liegt an der Atmosphäre, im Vakuum sehen wir nichts!). Wenn wir also den Laserstrahl verfolgen wollen, müssen wir in bestimmten Entfernungen im Raum Detektoren installieren, sinnvoller Weise Spiegel, anhand des so reflektierten Strahles würden wir aber feststellen, das sich die Detektoren aufgrund unserer Eigenbewegung von uns entfernen, was eine Rotverschiebung des Strahles zur Folge hätte.
Wir sehen also das Licht, wenn wir es registrieren, auf jeden Fall rotverschoben, egal, ob wir es als ursprünglich von einem entfernten Objekt kommend messen, oder ob wir das Licht erst von einer "heimischen" Quelle aussenden.
Es liegt an der Bewegung, dass das Licht rot- oder blauverschoben wird, das ist richtig, aber es hat nichts mit einem Energieverlust zu tun, Energie ist – ich muss mich wiederholen – eine Erhaltungsgröße, wir müssen also erklären, warum es eine Rot- oder Blauverschiebung gibt, und es gibt keine andere Erklärung als die sich vergrößernde bzw. verkleinernde Wegstrecke, die das Licht aufgrund der Bewegung zurückleben muss; und das liegt an der Konstanz der Lichtgeschwindigkeit, deshalb die Verschiebung.�
Beitrag 2058-23
-
Die Energieerhaltung bei der Rotverschiebung, auch die durch die Expansion des Universums verursachte, erklärt sich letztendlich dadurch, dass
Energie eine relative Größe ist. Und darum geht es im Titel des Threads: Ist Energie ebenso relativ wie Zeit und Raum?
Da meine bisherigen Erläuterungen wohl nicht verstanden wurden, hier folgendes Zitat aus
Wissenschaft Online (Autor ist der Astrophysiker Andreas Müller):
mfg okotombrok
Da meine bisherigen Erläuterungen wohl nicht verstanden wurden, hier folgendes Zitat aus
Wissenschaft Online (Autor ist der Astrophysiker Andreas Müller):
Zitat:Rot- und Blauverschiebungen bergen ein weiteres Verständnisproblem: Wo bleibt die Strahlungsenergie, wenn z.B. das stark rotverschobene Photon einer entfernten Galaxie auf der Erde ankommt?
Keine Sorge, der Energieerhaltungssatz wird nicht verletzt. Man darf eben nur die Energie im Bezugssystem Galaxie mit derjenigen im Bezugssystem Erde vergleichen, wenn man auch berücksichtigt, dass das Universum zum Zeitpunkt der Emission des Photons in der Galaxie ein anderes Universum war, als zum Zeitpunkt der Ankunft des Photons auf der Erde! Präzise gesagt unterscheiden sich beide Bezugssysteme im Skalenfaktor R(t), auch Weltradius genannt. 'Rotverschobene, kosmologische Photonen' sind ähnlich zu den 'gravitationsrotverschobenen Photonen' in einem Schwerefeld zu sehen. Denn die Strahlungsenergie geht in beiden Fällen an die (dynamische bzw. gekrümmte) Raumzeit verloren. Kosmologische Rotverschiebung und Gravitationsrotverschiebung sind rein geometrische Effekte.
Es spiegelt sich jedoch auch die Relativität des Beobachters darin wider, denn es spielt eine Rolle, in welchem Bezugssystem er sitzt.
mfg okotombrok
Beitrag 2058-24
Die 3 Varianten der Rotverschiebung wirklich genau erklärt
Danke, Okotombrok,
der Artikel in wissenschaft online ist wirklich hilfreich. Ich sehe die Sache jetzt also so:
Wo Rotverschiebung auftritt, ist sie Summe von insgesamt 3 Ursachen:
Im ersten Fall ist entsprechender Energieverlust der Photonen Umwandlung eines Teiles ihrer Energie in Druck, der die Raumzeit zunehmend "aufgeblasen" hält.
Im letzten Fall ist entsprechender Energieverlust einzig und allein auf die relative Sicht des Beobachters zurückzuführen, der das Licht rotverschoben sieht.
Wo er das Licht blauverschoben sieht, ist entsprechender Energiegewinn ebenfalls einfach nur dieser relativierten Sicht geschuldet.
Vielen Dank,
grtgrt
Danke, Okotombrok,
der Artikel in wissenschaft online ist wirklich hilfreich. Ich sehe die Sache jetzt also so:
Wo Rotverschiebung auftritt, ist sie Summe von insgesamt 3 Ursachen:
- kosmologischer Rotverschiebung,
- gravitativer Rotverschiebung (meist zu vernachlässigen) und
- lokaler Rotverschiebung aufgrund eines Dopplereffekts.
Im ersten Fall ist entsprechender Energieverlust der Photonen Umwandlung eines Teiles ihrer Energie in Druck, der die Raumzeit zunehmend "aufgeblasen" hält.
Im letzten Fall ist entsprechender Energieverlust einzig und allein auf die relative Sicht des Beobachters zurückzuführen, der das Licht rotverschoben sieht.
Wo er das Licht blauverschoben sieht, ist entsprechender Energiegewinn ebenfalls einfach nur dieser relativierten Sicht geschuldet.
Vielen Dank,
grtgrt
Beitrag 0-156
Genaueres zu den 3 Varianten der Rotverschiebung
Rotverschiebung kann 3 Ursachen haben
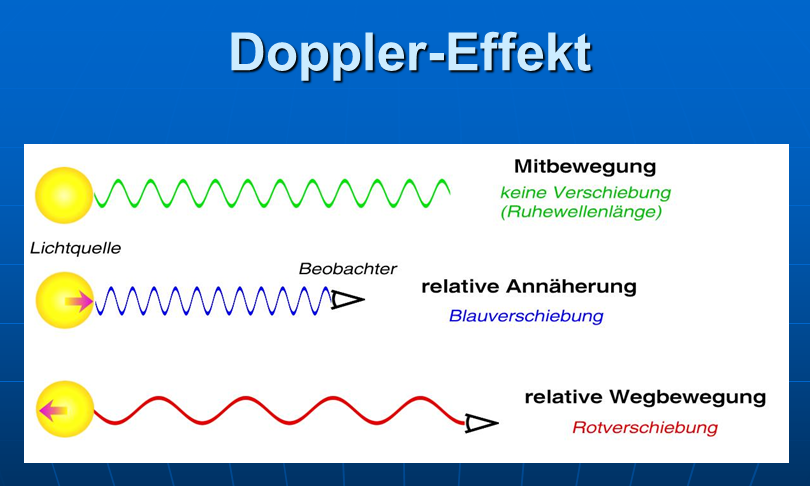
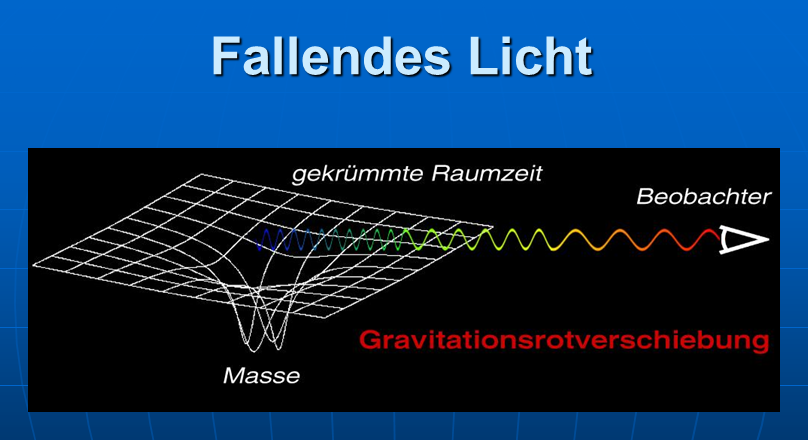
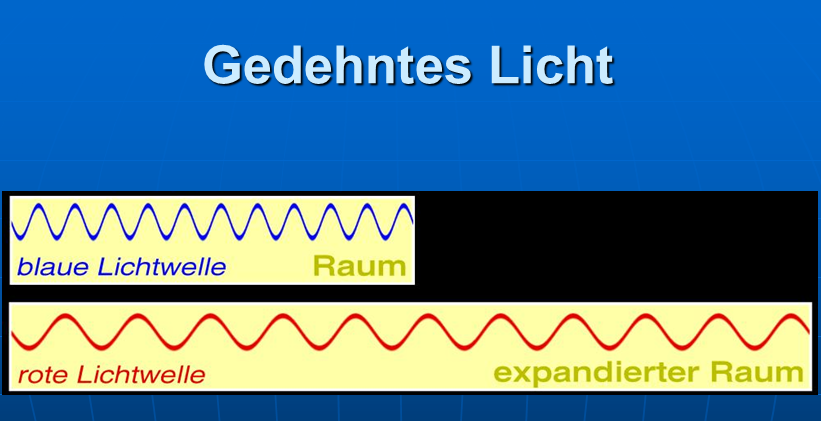
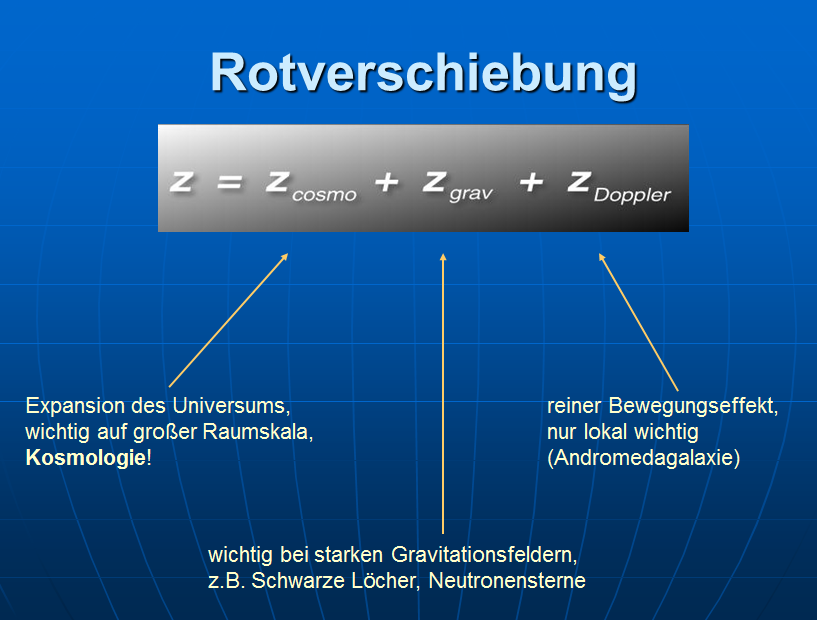
Quelle: Andreas Müller, Max-Planck-Institut für extraterrestrische Physik, Garching
Warum auf eine Gravitationsquelle zukommendes Licht blauverschoben, von ihr ausgesandtes aber rotverschoben ist, erklärt sehr schön Helmut Hetznecker auf den Seiten 82-84 seines Buches Kosmologische Strukturbildung, Spektrum-Verlag 2009:
Wie Einsteins Spezielle Relativitätstheorie zeigt, sind Masse und Energie äquivalent. Selbst Photonen haben demnach in einem Schwerefeld Gewicht.
Verlässt nun also ein Strahlungsquant den Potentialtopf einer Gravitationsquelle, so verliert es Energie — ganz so wie ein Ball, den man senkrecht nach oben wirft. Nun ist die Energie jeden Photons aber proportional zu seiner Frequenz. Sie also wird geringer (= rotverschoben), wenn das Photon sich von der Gravitationsquelle entfernt.




Quelle: Andreas Müller, Max-Planck-Institut für extraterrestrische Physik, Garching
Warum auf eine Gravitationsquelle zukommendes Licht blauverschoben, von ihr ausgesandtes aber rotverschoben ist, erklärt sehr schön Helmut Hetznecker auf den Seiten 82-84 seines Buches Kosmologische Strukturbildung, Spektrum-Verlag 2009:
Wie Einsteins Spezielle Relativitätstheorie zeigt, sind Masse und Energie äquivalent. Selbst Photonen haben demnach in einem Schwerefeld Gewicht.
Verlässt nun also ein Strahlungsquant den Potentialtopf einer Gravitationsquelle, so verliert es Energie — ganz so wie ein Ball, den man senkrecht nach oben wirft. Nun ist die Energie jeden Photons aber proportional zu seiner Frequenz. Sie also wird geringer (= rotverschoben), wenn das Photon sich von der Gravitationsquelle entfernt.
Beitrag 2113-1
Nachweis einer Klarstellung zur SRT
In Wikipedia wird völlig richtig erklärt:
Bewegte Uhren scheinen langsamer zu gehen:
Jeder Beobachter, relativ zu dem die Uhr sich bewegt, hat diesen Eindruck.
Das Ausmaß allerdings, in dem unterschiedliche Beobachter eine bewegte Uhr langsamer gehen sehen, kann von Beobachter zu Beobachter verschieden groß sein. Kurz:
Wie schnell ein Beobachter eine Uhr gehen sieht,
hängt davon ab, wie schnell er sich ihr gegenüber bewegt.
Man kann das einsehen wie folgt:
Kleine Übungsaufgabe:
Nun, Okotombrok,
so richtig verstanden hast Du die SRT wohl nicht, denn auch Physiker betonen, dass die SRT nur von beobachterspezifischen S i c h t e n spricht, aber keineswegs von Raumstruktur:
Quelle: Seite 212 des Buches Gottes unsichtbare Würfel von Helmut Satz (Verlag C.H. Beck 2013)
Der Autor — Helmut Satz — war von 1971 bis 2001 Professor für Theoretische Physik an der Universität Bielefeld.
Fast noch deutlicher wird Grtgrt bestätigt durch Bojowald:
Quelle: Seite 24 des Buches Zurück vor den Urknall von Martin Bojowald (Fischer Taschenbuchverlag, 3. Auflage 2012)
Martin Bojowald lehrt Theoretische Physik an der Penn State University, USA.
Völlig richtig wird der wahre Sachverhalt auch beschrieben durch Carrier. Seine Formulierung enthält auch eine Begründung:
Insbesondere sagt Carrier (nach Erklärung eines scheinbaren Paradoxons):
Quelle: Seite 33-39 des Buches Raum-Zeit von Martin Carrier (de Gruyter 2009)
Carrier ist Professor für Philosophie an der Universität Bielefeld mit Schwerpunkt Wissenschaftsphilosophie
Er begann seine Ausbildung mit einem Studium der Physik.
Man lese auch
Bewegte Uhren scheinen langsamer zu gehen:
Das Ausmaß allerdings, in dem unterschiedliche Beobachter eine bewegte Uhr langsamer gehen sehen, kann von Beobachter zu Beobachter verschieden groß sein. Kurz:
hängt davon ab, wie schnell er sich ihr gegenüber bewegt.
Man kann das einsehen wie folgt:
-
Hat man zwei Objekte, die sich mit konstanter Geschwindigkeit von einander weg bewegen, so wird jedes von beiden den Eindruck haben, die Zeit beim jeweils anderen vergehe langsamer.
Da sich diese beiden Beobachtungen aber widersprechen, steht fest, dass es sich hierbei um einen nur beobachtungstechnisch bedingten Effekt handelt: um ein Scheinergebnis,
welches sich der Realität des Beobachters zuordnet, aber nicht Wirklichkeit sein muss.
Und tatsächlich gilt ja im Rahmen von Einsteins Theorie immer:
Jede Beobachtung ist ihrem Ergebnis nach abhängig vom Bezugssystem, aus dem heraus der Beobachter argumentiert.
Anders gesagt: Wir sprechen stets nur über beobachterspezifische Realität
Kleine Übungsaufgabe:
-
Nimm an, wir hätten einen Schienenweg, der einen Kreis darstellt. Irgendwo auf dieser eingleisigen, kreisförmigen Strecke stehen zwei baugleiche Lokomotiven,
deren Rückseiten sich berühren und die zum selben Zeitpunkt
in entgegengesetzte Richtung abfahren, stets identisch beschleunigt werden, aber anhalten in dem Moment, in dem sie sich wieder berühren (sie kommen ja nicht an einander vorbei).
Beide, so nehmen wir an, transportieren baugleiche Uhren, die beim Start der Lokomotiven 12:00 zeigten.
- die jeweils andere langsamer ging, solange der Abstand zwischen ihnen sich vergrößert hat
- bzw. schneller ging, sobald der Abstand zwischen ihnen sich wieder verkleinerte.
FRAGE: Werden die beiden Uhren unterschiedliche Zeit anzeigen, wenn die beiden Lokomotiven wieder aufeinander treffen? (Sie werden dann jeweils genau gleich weit gefahren sein.) Wie verträgt sich deine Antwort mit der Tatsache, dass während der Fahrt aus Sicht jeder der beiden Uhren
Okotombrok in 1997-99:
Grtgrt in 1997-94:
Das Szenario symmetrisch zu machen erlaubt uns zu erkennen, dass — in der SRT —
die beobachtete Zeitdilation nur in den S i c h t e n der beiden Beobachter auftritt, aber eben n i c h t in der Raumzeit selbst.
Dummes Zeug,
das einzige, was dein Szenario erkennen lässt ist, dass unter gleichen Bedingungen Bedingungen herrschen, die zu gleichen Bedingungen führen.
Nun, Okotombrok,
so richtig verstanden hast Du die SRT wohl nicht, denn auch Physiker betonen, dass die SRT nur von beobachterspezifischen S i c h t e n spricht, aber keineswegs von Raumstruktur:
Zitat von Helmut Satz (2013):
Wenn in einem Raumschiff, das sich mit einer hohen konstanten Geschwindigkeit v relativ zur Erde bewegt, die Lichtgeschwindigkeit c die gleiche ist, wie in einem irdischen Labor, dann muss aus unserer Sicht das Längenmaß des Raumschiffes kürzer sein als unseres oder deren Uhr muss langsamer sein als unsere oder beides.
In der Tat tritt beides auf. Ein festes Maß d0. ein Standardmeter, hat den gleichen Wert für uns hier wie für die Passagiere des Raumschiffs.
Aber von uns aus gemessen erscheint deren Standardmeter d0 auf eine Länge d geschrumpft
d = d0 • ( 1 – (v/c)2 )1/2
Und ein festes Zeitintervall t0 erscheint, von der Erde ais gesehen, länger geworden zu sein, den Wert
t = t0 • ( 1 – (v/c)2 )–1/2
zu haben.
Der Autor — Helmut Satz — war von 1971 bis 2001 Professor für Theoretische Physik an der Universität Bielefeld.
Fast noch deutlicher wird Grtgrt bestätigt durch Bojowald:
Zitat von Martin Bojowald (2008):
Wenn wir uns beim Betrachten einer Situation schneller bewegen als ein zweiter Beobachter, so erscheinen uns räumliche und zeitliche Abstände in den beobachteten Ereignissen anders als diesem.
Wie ein Wechsel des Sichtwinkels die räumlichen Ausdehnungen ineinander überführt, so wandelt ein Ändern der Geschwindigkeit beim Beobachten räumliche in zeitliche Abstände um und umgekehrt.
Aus diesem Grunde ist die Unterscheidung zwischen räumlicher und zeitlicher Ausdehnung vom Standpunkt (oder genauer von der "Standbahn", wenn wir uns wirklich bewegen) abhängig und hat keine physikalische Basis unabhängig von Beobachtern. Anstatt Raum und Zeit zu trennen, gibt es nur ein einziges gemeinsames Objekt: die Raumzeit.
Martin Bojowald lehrt Theoretische Physik an der Penn State University, USA.
Völlig richtig wird der wahre Sachverhalt auch beschrieben durch Carrier. Seine Formulierung enthält auch eine Begründung:
Zitat von Martin Carrier (2009):
Kennzeichnend für die SRT ist der Vorrang raumzeitlicher Größen vor ihren räumlichen und zeitlichen Bestandteilen. Dieser Primat der 4-dimensionalen Größen wurde zuerst 1908 von Minkowski hervorgehoben: Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.
Minkowski erkannte, dass sich die SRT als eine spezifische, neuartige Geometrie darstellen lässt, in der die raumzeitlichen Abstände eine zentrale Stellung insofern einnehmen, als sie die o b j e k t i v e n Beziehungen zwischen Ereignissen wiedergeben, während deren räumliche und zeitliche Bestimmungsstücke vom Bewegungszustand des Beobachters abhängen und in diesem Sinne s u b j e k t i v sind.
Genauer: Der [mit Hilfe der Minkowski-Metrik errechnete] Viererabstand ist die zentrale Größe der Raumzeit der SRT. Im Unterschied zur Raum-Zeit der klassischen Physik bleibt allein diese Größe bei einem Wechsel des Inertialsystems erhalten — nicht aber der 3-dimensionale räumliche Abstand oder der 1-dimensionale zeitliche.
Wegen dieser Invarianz ist der Viererabstand fundamentaler [ der Wirklichkeit näher ] als die vom Bezugssystem abhängigen räumlichen und zeitlichen Größen.
Dennoch ist es nicht die 4-Dimensionalität als solche, die die Relativitätstheorie auszeichnet: Auch Ereignisse in der Newtonschen Raum-Zeit werden ja erst durch 3 Ortskoordinaten und eine Zeitkoordinate vollständig lokalisiert. Kennzeichnend für die SRT ist vielmehr der Vorrang raumzeitlicher Größen vor ihren räumlichen und zeitlichen Bestandteilen. ...
Insofern beinhaltet der Übergang von der Newtonschen zur Einsteinschen Raumzeit die Ersetzung 3-dimensionaler bzw. 1-dimensionaler absoluter Größen durch jeweils nur e i n e 4-dimensionale absolute Größe.
Insbesondere sagt Carrier (nach Erklärung eines scheinbaren Paradoxons):
Zitat von Martin Carrier (2009):
Deutlich wird, dass die relativistische Längenkontraktion eine Folge des Verfahrens der Längenmessung ist.
Carrier ist Professor für Philosophie an der Universität Bielefeld mit Schwerpunkt Wissenschaftsphilosophie
Er begann seine Ausbildung mit einem Studium der Physik.
Man lese auch
- G. Greiter: Relativitätstheorie beschreibt beobachterspezifische Realität
- G. Greiter: Zeitdilatation im Sinne der Theorien Einsteins
Beitrag 1997-134
Wo selbst Physikern die Grenzen der SRT nicht so ganz klar zu sein scheinen
Hallo Eugen,
erst mal vielen Dank für Deine Mühe. Ich weiß sie sehr zu schätzen!
Nun aber lass mich dazu Stellung beziehen (Ausgangspunkt können heute nur die Zitate selbst sein, denn keines jener Bücher habe ich zu Hause):
Zunächst mal ist festzustellen, dass wir beide hier etwas sehr Interessantes entdeckt haben:
Die unterschiedliche Überzeugung, die hier im Forum die beiden Gruppen an Physik interessierter Laien
{ Bauhof, Stueps, Henry, Okotombrok } vs { Grtgrt, Harti }
auseinander dividiert, besteht offenbar auch zwischen den beiden folgenden Gruppen von Physik-Professoren:
{ D.Giulini & T.Filk + C.Kiefer + E.Rebhan } vs { W.Greiner & J.Rafelski }.
Um zu sehen, wer recht hat, müssen wir jetzt also tatsächlich die Argumentation aller viel genauer als bisher betrachten, um zu sehen, wo die eine oder andere lückenhaft oder nicht nachvollziehbar ist. Tun wir das:
Allen — den Professoren ebenso wie uns hier im Forum — ist gemeinsam, dass wir wissen: Wo die Situation, die zum sog. Zwillingsparadoxon führt (kurz: SZw), in der Wirklichkeit nachgestellt wird, werden die beiden Zwillinge mindestens zeitweise unterschiedlichen Beschleunigungskräften ausgesetzt sein. Schon allein deswegen wird jeder Logiker uns sagen: Da die SRT Situationen, in denen es zu beschleunigter Bewegung kommt, gar nicht vorgibt, noch behandeln zu können, kann sie auf Situation SZw auch gar nicht anwendbar sein.
Nun könnte man aber argumentieren, dass die SRT, wenn man genauer hinsieht, vielleicht auch beschleunigte Situationen noch behandeln könnte (dass also Einstein und Minkowski, die Einschränkung, nur gleichförmige Bewegung zuzulassen, vielleicht gar nicht hätten machen müssen).
Jeder, der behauptet, auch die SRT würde beweisen, dass die Zwillinge, wenn sie sich wieder treffen, unterschiedlich alt sind, geht — implizit oder explizit — von dieser Annahme aus — hat dann aber auch die Pflicht, sie zu beweisen.
Die Zitate [1] und [2] skizzieren den Ansatz solcher Beweisversuche, sind aber nicht detailliert genug, mir zu zeigen, ob jene "Beweise" auch wirklich schlüssig sind.
Im Zitat [3] wird durch Rebhan explizit versucht, die SRT so zu erweitern, dass sie auch noch auf beschleunigte Bewegung anwendbar ist. Dies, so wird behauptet, gelänge über Anwendung eines mathematischen Grenzprozesses. Zwei Aussagen aus diesem Beweisversuch aber finde ich nicht wirklich nachvollziebar. Es sind die jetzt im Zitat rot hervorgehobenen Teile:
Zitat [4] schließlich begündet die Meinung der Autoren nur in Form einer (als "offensichtlich wahr" hingestellten) V e r m u t u n g (und ist deswegen nicht ernst zu nehmen. Die Autoren scheinen Gymnasiallehrer zu sein, Personen also, die wohl auch nicht kompetenter sind als an Relativitätstheorie ernsthaft interessierte Laien.
Dem Zitat aus [5] schließlich kann ich gar nicht entnehmen, dass der Autor — Ulrich Schröder — es für zweifelsfrei erwiesen hält, dass die SRT auf die Situation beschleunigter Bewegung in irgendeiner sinnvollen Verallgemeinerung ihrer selbst (der SRT) anwendbar wird. Er weist lediglich mit Bestimmheit darauf hin, dass in der realen Wirklichkeit unser Welt (wie Hafele & Keating zeigen konnten) es tatsächlich zu unterschiedlich schneller Alterung zweier Objekte kommen kann.
[1] Giulini, Domenico und Filk, Thomas: Am Anfang war die Ewigkeit. Auf der Suche nach dem Ursprung der Zeit.
München 2004
ISBN=3-406-52187-8
[2] Kiefer, C...: Der Quantenkosmos.
Frankfurt am Main 2008
ISBN=978-3-10-039506-1
[3] Rebhan, Eckhard: Theoretische Physik. Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999
ISBN=3-8274-0246-8
[4] Beyvers, Gottfried und Kusch, Elvira: Kleines 1 x 1 der Relativitätstheorie. Einsteins Physik mit Mathematik der Mittelstufe.
Berlin 2009
ISBN=978-3-540-85202-5
[5] Schröder, Ulrich E.: Spezielle Relativitätstheorie (Vierte Auflage)
Frankfurt am Main 2005
ISBN=3-8171-1724-8
Wenn wir uns jetzt im Gegenzug auch mein Argument aus Beitrag 1997-114 nochmals vornehmen, so wird klar:
Meine Argumentation benötigt, um gültig zu sein, nur eine einzige Voraussetzung:
Die Konstanz und Endlichkeit der Lichtgeschwindigkeit.
Sie ist deswegen sogar noch auf beschleunigte Bewegungen anwendbar und zwar ganz unabhängig davon, ob beide Zwillinge oder nur einer beschleunigt wird.
So lange mir also in eben dieser Argumentation niemand einen Fehler aufzeigen kann, sehe ich sie als wunderbar einfache Bestätigung der Meinung von W.Greiner und J.Rafelski.
Auch wenn man nachsieht, wie renommiert die einzelnen Professoren sind, stehen da W.Greiner & J.Rafelski mit Sicherheit an der Spitze.
Damit, Eugen, bleibt mir vernünftiger Weise gar nichts anderes übrig, als zunächst mal zu glauben, dass diese beiden — und damit auch ich — recht haben.
Mit besten Grüßen,
Gebhard (grtgrt)
Hallo Harti,
auch nachdem Okotombrok das Thema 1997 für jede weitere Äußerung gesperrt hat, bin ich der Frage, ob das Zwillingsparadoxon per SRT lösbar ist, weiter nachgegangen und weiß nun, dass Du und ich — aber dennoch auch die anderen — recht hatten.
Es gilt nämlich:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch zutreffende Aussagen darüber machen kann, wie Beschleunigung sich auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche auf dem Hintergrund der Raumzeit der SRT errechneten Ergebnisse tatsächlich (grob wenigstens) mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrunde liegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt zudem sehr klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
ausschließlich auf jene Phasen der Reise zurückführt, in denen die beiden Zwillinge unterschiedlich beschleunigt waren.
Damit steht fest:
Hierbei allerdings muss berücksichtigt werden:
Diesen wesentlichen Unterschied nicht zu übersehen, macht es schon Sinn, über beschleunigte Bewegungen tatsächlich nur mit Hilfe der ART nachzudenken. Siehe dazu auch Bemerkungen auf gutefrage.net.
Man sieht hier sehr schön, dass unterschiedlich genaue physikalische Modelle — SRT und ART — eben auch unterschiedlich genaue Aussagen machen.
Beste Grüße,
grtgrt
Bauhof in 1997-122:
Grtgrt in 1997-121:Hi Eugen,
wenn du mir Links auf jene Stellen geben kannst — oder sie in Büchern zu finden sind, auf die ich Zugriff habe — werde ich sie mir ganz bestimmt ansehen.
Hallo Grtgrt,
gut, ich mache mir mal die Mühe und gebe dir die entsprechenden Hinweise als Zitate aus meinen Büchern. Keiner der aufgeführten Autoren gibt einen Hinweis darauf, dass das Zwillingsparadoxon nur mit Hilfe der ART gelöst werden könnte. Sie argumentieren alle mit Hilfe der SRT.
Hallo Eugen,
erst mal vielen Dank für Deine Mühe. Ich weiß sie sehr zu schätzen!
Nun aber lass mich dazu Stellung beziehen (Ausgangspunkt können heute nur die Zitate selbst sein, denn keines jener Bücher habe ich zu Hause):
Zunächst mal ist festzustellen, dass wir beide hier etwas sehr Interessantes entdeckt haben:
Um zu sehen, wer recht hat, müssen wir jetzt also tatsächlich die Argumentation aller viel genauer als bisher betrachten, um zu sehen, wo die eine oder andere lückenhaft oder nicht nachvollziehbar ist. Tun wir das:
Allen — den Professoren ebenso wie uns hier im Forum — ist gemeinsam, dass wir wissen: Wo die Situation, die zum sog. Zwillingsparadoxon führt (kurz: SZw), in der Wirklichkeit nachgestellt wird, werden die beiden Zwillinge mindestens zeitweise unterschiedlichen Beschleunigungskräften ausgesetzt sein. Schon allein deswegen wird jeder Logiker uns sagen: Da die SRT Situationen, in denen es zu beschleunigter Bewegung kommt, gar nicht vorgibt, noch behandeln zu können, kann sie auf Situation SZw auch gar nicht anwendbar sein.
Nun könnte man aber argumentieren, dass die SRT, wenn man genauer hinsieht, vielleicht auch beschleunigte Situationen noch behandeln könnte (dass also Einstein und Minkowski, die Einschränkung, nur gleichförmige Bewegung zuzulassen, vielleicht gar nicht hätten machen müssen).
Jeder, der behauptet, auch die SRT würde beweisen, dass die Zwillinge, wenn sie sich wieder treffen, unterschiedlich alt sind, geht — implizit oder explizit — von dieser Annahme aus — hat dann aber auch die Pflicht, sie zu beweisen.
Die Zitate [1] und [2] skizzieren den Ansatz solcher Beweisversuche, sind aber nicht detailliert genug, mir zu zeigen, ob jene "Beweise" auch wirklich schlüssig sind.
Im Zitat [3] wird durch Rebhan explizit versucht, die SRT so zu erweitern, dass sie auch noch auf beschleunigte Bewegung anwendbar ist. Dies, so wird behauptet, gelänge über Anwendung eines mathematischen Grenzprozesses. Zwei Aussagen aus diesem Beweisversuch aber finde ich nicht wirklich nachvollziebar. Es sind die jetzt im Zitat rot hervorgehobenen Teile:
Zitat:
Wir betrachten noch die kurzen Beschleunigungsphasen der Rakete im Inertialsystem der Erde. Diese können wir stückweise aus Teilen zusammensetzen, während deren die Geschwindigkeit annähernd konstant ist. Da diese jeweils kleiner als die Fluggeschwindigkeit v ist, ergibt sich für die Dauer einer ganzen Beschleunigungsphase im Mittel eine kleinere Zeitdilatation als für eine gleich lange Flugphase mit der konstanten Reisegeschwindigkeit. Lassen wir jetzt die Beschleunigung gegen unendlich und die Beschleunigungsdauer gegen null gehen, so geht auch die diktierte Beschleunigungsdauer gegen null.
Man könnte vermuten, dass dem Effekt der SRT auch noch Effekte der ART überlagert sind. Wir werden später allerdings sehen, dass das nur der Fall ist, wenn Schwerefelder involviert sind, ansonsten bleibt die oben angestellte Überlegung richtig. Man kann sich aber auch schon, ohne Genaueres über ART-Effekt zu wissen, darüber klar werden, dass diese bei einer langen Raumfahrt keine Rolle spielen. Um das einzusehen, nehmen wir an, für den Zwilling auf der Erde sei die Dauer einer Beschleunigungsphase dt, für den im Raumschiff unter Einbezug von ART-Effekten dt'. Aus der Homogenität der Zeit folgt, dass der Quotient dt'/dt nur von der Art des Beschleunigungsprozesses abhängt, nicht aber von dem Zeitpunkt, zu dem er durchgeführt wird. Die Raumfahrt enthält vier gleichartige Beschleunigungsprozesse, die Geschwindigkeit des Raumschiffes geht von
0 → vmax → 0 → vmax → 0
Damit ergibt sich als Altersunterschied der Zwillinge
D = ( T – T' ) + 4( dt – dt' )
Der Anteil ( T – T' ) wächst mit der Dauer der Raumfahrt, während der Anteil 4( dt – dt' ) konstant ist. Er kann durch ein Differenzexperiment zum Verschwinden gebracht werden; in einem Einzelexperiment wird er vernachlässigbar, wenn die Raumfahrt hinreichend lange dauert. Für unsere weiteren Überlegungen machen wir die letzte Annahme.
Zitat [4] schließlich begündet die Meinung der Autoren nur in Form einer (als "offensichtlich wahr" hingestellten) V e r m u t u n g (und ist deswegen nicht ernst zu nehmen. Die Autoren scheinen Gymnasiallehrer zu sein, Personen also, die wohl auch nicht kompetenter sind als an Relativitätstheorie ernsthaft interessierte Laien.
Dem Zitat aus [5] schließlich kann ich gar nicht entnehmen, dass der Autor — Ulrich Schröder — es für zweifelsfrei erwiesen hält, dass die SRT auf die Situation beschleunigter Bewegung in irgendeiner sinnvollen Verallgemeinerung ihrer selbst (der SRT) anwendbar wird. Er weist lediglich mit Bestimmheit darauf hin, dass in der realen Wirklichkeit unser Welt (wie Hafele & Keating zeigen konnten) es tatsächlich zu unterschiedlich schneller Alterung zweier Objekte kommen kann.
[1] Giulini, Domenico und Filk, Thomas: Am Anfang war die Ewigkeit. Auf der Suche nach dem Ursprung der Zeit.
München 2004
ISBN=3-406-52187-8
[2] Kiefer, C...: Der Quantenkosmos.
Frankfurt am Main 2008
ISBN=978-3-10-039506-1
[3] Rebhan, Eckhard: Theoretische Physik. Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999
ISBN=3-8274-0246-8
[4] Beyvers, Gottfried und Kusch, Elvira: Kleines 1 x 1 der Relativitätstheorie. Einsteins Physik mit Mathematik der Mittelstufe.
Berlin 2009
ISBN=978-3-540-85202-5
[5] Schröder, Ulrich E.: Spezielle Relativitätstheorie (Vierte Auflage)
Frankfurt am Main 2005
ISBN=3-8171-1724-8
Wenn wir uns jetzt im Gegenzug auch mein Argument aus Beitrag 1997-114 nochmals vornehmen, so wird klar:
Die Konstanz und Endlichkeit der Lichtgeschwindigkeit.
Sie ist deswegen sogar noch auf beschleunigte Bewegungen anwendbar und zwar ganz unabhängig davon, ob beide Zwillinge oder nur einer beschleunigt wird.
So lange mir also in eben dieser Argumentation niemand einen Fehler aufzeigen kann, sehe ich sie als wunderbar einfache Bestätigung der Meinung von W.Greiner und J.Rafelski.
Auch wenn man nachsieht, wie renommiert die einzelnen Professoren sind, stehen da W.Greiner & J.Rafelski mit Sicherheit an der Spitze.
Damit, Eugen, bleibt mir vernünftiger Weise gar nichts anderes übrig, als zunächst mal zu glauben, dass diese beiden — und damit auch ich — recht haben.
Mit besten Grüßen,
Gebhard (grtgrt)
Harti in Beitrag Nr. 1197-119:
Hallo Grtgrt,
lass Dich durch das Etikett "Einstein-Widerleger" nicht ins Boxhorn jagen. Selbstverständlich kann man das Zwillingsparadoxon nur mit Hilfe der ART lösen.
Hallo Harti,
auch nachdem Okotombrok das Thema 1997 für jede weitere Äußerung gesperrt hat, bin ich der Frage, ob das Zwillingsparadoxon per SRT lösbar ist, weiter nachgegangen und weiß nun, dass Du und ich — aber dennoch auch die anderen — recht hatten.
Es gilt nämlich:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch zutreffende Aussagen darüber machen kann, wie Beschleunigung sich auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche auf dem Hintergrund der Raumzeit der SRT errechneten Ergebnisse tatsächlich (grob wenigstens) mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrunde liegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt zudem sehr klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
Damit steht fest:
- Wer von der SRT (in Einsteins Fassung) ausgeht, geht von einer Theorie aus, die zu beschleunigten Bewegungen nichts aussagen will und demnach auf die Situation des Zwillingsparadoxon gar nicht anwendbar ist.
- Seit etwa 2000 aber geht man nicht mehr davon aus, dass die SRT — wenn man versucht, sie auch auf beschleunigte Bewegung anzuwenden — falsche Aussagen macht. Soweit man nämlich Beispiele in SRT u n d ART durchgerechnet hat, kam man zum gleichen Ergebnis (was aber nicht heißt, dass wirklich alles, was die ART sagt, auch mit Mitteln der SRT nachrechenbar wäre).
- Es kommt hier wohl die Tatsache zum Tragen, dass in jeder hinreichend kleinen Umgebung eines nicht singulären Punktes P der Raumzeit der ART die SRT sehr gute Approximation der ART ist.
Hierbei allerdings muss berücksichtigt werden:
-
Wer im Rahmen der SRT auch beschleunigte Bewegungen betrachtet, sieht die Beschleunigung einfach nur als erste Ableitung der Geschwindigkeit nach der Zeit —
er sieht sie dann also noch nicht — wie die ART es tut — auch als physikalisches Phänomen äquivalent zu einer Krümmung der Raumzeit.
Diesen wesentlichen Unterschied nicht zu übersehen, macht es schon Sinn, über beschleunigte Bewegungen tatsächlich nur mit Hilfe der ART nachzudenken. Siehe dazu auch Bemerkungen auf gutefrage.net.
Man sieht hier sehr schön, dass unterschiedlich genaue physikalische Modelle — SRT und ART — eben auch unterschiedlich genaue Aussagen machen.
Beste Grüße,
grtgrt
Beitrag 0-144
Die zentralen Aussagen von Einsteins Relativitätstheorie
Spezielle Relativitätstheorie sagt:
Unabhängig vom Zustand eines Beobachters wird das Licht sich relativ zu ihm mit stets gleicher Geschwindigkeit bewegen. Daraus folgt:
Sind A und B zwei relativ zueinander bewegte identisch gebaute Objekte, die jeweils identisch gebaute Uhren enthalten, so werden — nur aus Sicht von B —
Diese Unterschiede sind nur beobachtungstechnisch begründete Unterschiede, die zustande kommen, weil die Lichtgeschwindigkeit endlich ist.
Dies nämlich bewirkt, dass fern vom Beobachter eintretende Ereignisse ihm erst als etwas später eingetreten erscheinen und dieser Zeitverzug umso größer sein wird, je weiter entfernt vom Beobachter das Ereignis stattfindet.
Und natürlich gilt, dass umgekehrt aus Sicht von A
Mehr dazu findet sich erklärt auf Seite » Relativitätstheorie beschreibt beobachterspezifische Realität «.
Konsequenz aus all dem:
Jede Quantifizierung von Zeit oder Masse (= Objektenergie) ist relativ,
d.h. abhängig davon, wie sich das beobachtete Objekt relativ zum Beobachter bewegt.
Beweis: Die Objektenergie ergibt sich als Summe der Bewegungsenergie des Objekts (die relativ ist, da alle Geschwindigkeit relativ ist) und der Ruheenergie des Objekts (welche seine Ruhemasse multipliziert mit dem Quadrat der Lichtgeschwindigkeit ist).
Wichtiger Hinweis:
In » The Concept of Mass in the Einstein Year « liest man (zu Beginn von Kapitel 5 auf Seite 16):
Lies mehr dazu auf Seite » Relativistische Dynamik «
Unabhängig vom Zustand eines Beobachters wird das Licht sich relativ zu ihm mit stets gleicher Geschwindigkeit bewegen. Daraus folgt:
Sind A und B zwei relativ zueinander bewegte identisch gebaute Objekte, die jeweils identisch gebaute Uhren enthalten, so werden — nur aus Sicht von B —
- die Uhr von A langsamer gehen als die Uhr von B,
- alle Abstände auf A in Bewegungsrichtung verkürzt sein
- und A — wieder nur aus Sicht von B — mehr Masse haben als B.
Diese Unterschiede sind nur beobachtungstechnisch begründete Unterschiede, die zustande kommen, weil die Lichtgeschwindigkeit endlich ist.
Dies nämlich bewirkt, dass fern vom Beobachter eintretende Ereignisse ihm erst als etwas später eingetreten erscheinen und dieser Zeitverzug umso größer sein wird, je weiter entfernt vom Beobachter das Ereignis stattfindet.
Und natürlich gilt, dass umgekehrt aus Sicht von A
- die Uhr von B langsamer geht als die von A,
- alle Abstände auf B in Bewegungsrichtung verkürzt sind
- und B mehr Masse hat als A.
Mehr dazu findet sich erklärt auf Seite » Relativitätstheorie beschreibt beobachterspezifische Realität «.
Konsequenz aus all dem:
Jede Quantifizierung von Zeit oder Masse (= Objektenergie) ist relativ,
d.h. abhängig davon, wie sich das beobachtete Objekt relativ zum Beobachter bewegt.
Beweis: Die Objektenergie ergibt sich als Summe der Bewegungsenergie des Objekts (die relativ ist, da alle Geschwindigkeit relativ ist) und der Ruheenergie des Objekts (welche seine Ruhemasse multipliziert mit dem Quadrat der Lichtgeschwindigkeit ist).
Wichtiger Hinweis:
-
Wer von » Masse « spricht, kann damit entweder die relativistische (reale) Masse eines Objekts meinen (wie wir hier) oder seine Ruhemasse.
Nur letztere ist aus Sicht aller Beobachter — d.h. bezogen auf jedes Bezugssystem — gleich.
Einstein hat dafür plädiert, nur die Ruhemasse als Masse zu bezeichnen (siehe Wechsel im Wortgebrauch).
Wer sicher sein möchte, immer richtig verstanden zu werden, der sollte den Begriff » Masse « gar nicht mehr gebrauchen, sondern einfach nur noch die Begriffe Energie und Ruhemasse.
In » The Concept of Mass in the Einstein Year « liest man (zu Beginn von Kapitel 5 auf Seite 16):
L.B. Okun (2006, 2008):
The relation discovered by Einstein is not E = mc2 , but E0 = mc2 , where E0 is the energy of a free body at rest introduced by Einstein in 1905.
Beitrag 0-433
Der Zeitpunkt, zu dem — aus Sicht von Einsteins Relativitätstheorie — ein Ereignis eintritt
Der Zeitpunkt, zu dem ein Ereignis eintritt
Der Zeitpunkt, zu dem ein Ereignis E durch einen Beobachter B beobachtet wird — in dem Sinne, dass ihn Licht oder eine Gravitationswelle erreicht, das bzw. die durch E abgestrahlt wurde — ist der Zeitpunkt, zu dem sich E frühest möglich dem B bekannt gemacht haben kann.
Wer weiß, wie lange diese Nachricht unterwegs war — d.h., wer weiß, wie weit Ort(B) von Ort(E) in räumlicher Hinsicht entfernt ist — wird wissen, wann E eintrat.
Kein Signal kann sich schneller ausbreiten als Licht im Vakuum.
Der Endlichkeit der Lichtgeschwindigkeit wegen hat das folgende Konsequenzen:
Die Zeit eines Objektes X, welches sich von einen Beobachter B weg bewegt, wird — aus Sicht von B — langsamer vergehen als seine eigene Zeit.
Die Zeit eines Objektes X, welches sich auf einen Beobachter B zu bewegt, wird — aus Sicht von B — schneller vergehen als seine eigene Zeit.
Mit » aus Sicht von B « ist hier die rein nur beobachtungstechnische Sicht gemeint.
Nebenbei noch:
Der Zeitpunkt, zu dem ein Ereignis E durch einen Beobachter B beobachtet wird — in dem Sinne, dass ihn Licht oder eine Gravitationswelle erreicht, das bzw. die durch E abgestrahlt wurde — ist der Zeitpunkt, zu dem sich E frühest möglich dem B bekannt gemacht haben kann.
Wer weiß, wie lange diese Nachricht unterwegs war — d.h., wer weiß, wie weit Ort(B) von Ort(E) in räumlicher Hinsicht entfernt ist — wird wissen, wann E eintrat.
Kein Signal kann sich schneller ausbreiten als Licht im Vakuum.
Die Zeit eines Objektes X, welches sich von einen Beobachter B weg bewegt, wird — aus Sicht von B — langsamer vergehen als seine eigene Zeit.
Die Zeit eines Objektes X, welches sich auf einen Beobachter B zu bewegt, wird — aus Sicht von B — schneller vergehen als seine eigene Zeit.
Mit » aus Sicht von B « ist hier die rein nur beobachtungstechnische Sicht gemeint.
Nebenbei noch:
-
Was nach Einstein unter
» Gleichzeitigkeit «
verstanden werden sollte, beschrieb er
schon 1905 in §1 seiner Schrift
Zur Elektrodynamik bewegter Körper.
Beitrag 0-178
Die Natur kennt keine Zeit — sie kennt nur objektspezifische Eigenzeit (= Alter)
Wirklich ist nur Alter — aber nicht die Zeit
Immer noch kann die Theoretische Physik nicht beantworten, was denn nun eigentlich das wahre Wesen der Zeit ist. Der gegenwärtige Stand der Diskussion findet sich — gezielt vollständig und sehr genau — aufgeschrieben in den Büchern
Meiner Ansicht nach aber haben Einstein und die Quantenphysik das Rätsel um die Zeit längst gelöst, denn:
Die Natur kennt keine Zeit — sie kennt nur Alter
im Sinne von » Eigenzeit «
Beweis hierfür ist folgende Argumentation:
Einstein und Bohr haben uns gelehrt, dass es zwischen Wirklichkeit und Realität einen ganz gravierenden Unterschied gibt:
Nun weiß man aber:
Nebenbei: Auf die Frage, » Was ist Zeit? « soll Einstein einmal geantwortet haben » Zeit ist, was man von der Uhr abliest «. Wie meine Argumentation oben zeigt, wissen wir jetzt, dass Einstein damit recht hatte — und das wirklich im buchstäblichen Sinne. Was er sagte, war ganz offenbar mehr als nur eine flapsige Bemerkung (wie klar auch immer ihm selbst das gewesen sein mag). Sein Gefühl dafür, was physikalisch richtig sein mag, war einzigartig.
Da wir jetzt also wissen, dass Zeit stets nur das subjektiv gefärbte Ergebnis einer Beobachtung von Eigenzeit ist, stellt sich die Frage, warum wir sie in unserem Alltagsleben dennoch dermaßen erfolgreich nutzen. Das aber liegt daran,
Nebenbei noch: Was für das Paar Zeit und Eigenzeit richtig ist, gilt natürlich auch für das Paar Länge und Abstand: Länge ist das beobachterspezifisch subjektiv gefärbte Ergebnis einer Beobachtung von Abstand.
Mit der hier angesprochenen beobachterspezifischen Subjektivität ist natürlich stets das vom Beobachter gewählte Bezugssystem gemeint.
Natürlich lässt sich der eben beschriebene Sachverhalt aber auch über die Physik hinaus noch als richtig erkennen: Je spannender die Tätigkeit ist, die ein Mensch gerade ausübt, desto schneller wird ihm — seinem Gefühl nach — die Zeit vergehen. Ursache so entstandener Subjektivität ist dann (z.B.), wie oft jene Person sich gedrängt fühlt, auf eine Uhr zu sehen.
Nebenbei noch: Wie wir jetzt wissen, muss Einsteins Ausspruch
Zeit ist, was man von der Uhr abliest.
verstanden werden als
Zeit ist stets nur, was man von der eigenen Uhr abliest.
Letztlich ist jedes Objekt seine eigene Uhr.
Und tatsächlich schrieb Einstein (1905 in seinem Aufsatz Zur Elektrodynamik bewegter Körper): "Es könnte scheinen, dass alle die Definition der Zeit betreffenden Schwierigkeiten dadurch überwunden werden können, dass ich an Stelle der Zeit die Stellung des kleinen Zeigers meiner Uhr setze."
Da beschleunigte Objekte im Vergleich zu nicht beschleunigten aus der Sicht Dritter weniger schnell altern, sind die Entfernungen, die ein Mensch während seines Lebens im Prinzip überwinden kann, nur deswegen begrenzt, weil sein Organismus nur begrenzt hohe Beschleunigung auszuhalten im Stande ist.
Für Objekte, die sich mit Lichtgeschwindigkeit bewegen, gibt es keine Zeit.
Immer noch kann die Theoretische Physik nicht beantworten, was denn nun eigentlich das wahre Wesen der Zeit ist. Der gegenwärtige Stand der Diskussion findet sich — gezielt vollständig und sehr genau — aufgeschrieben in den Büchern
- Lee Smolin: Time Reborn: From the Crisis in Physics to the Future of the Universe (2013) und
- Roberto Mangabeira Unger & Lee Smolin: The Singular Universe and the Reality of Time: A Proposal in Natural Philosophy (2014)
Meiner Ansicht nach aber haben Einstein und die Quantenphysik das Rätsel um die Zeit längst gelöst, denn:
im Sinne von » Eigenzeit «
Beweis hierfür ist folgende Argumentation:
Einstein und Bohr haben uns gelehrt, dass es zwischen Wirklichkeit und Realität einen ganz gravierenden Unterschied gibt:
- Wirklichkeit ist das objektiv Vorhandene (dessen Funktionsweise wir aber nicht kennen),
- Realität aber ist der Menschen subjektive Sicht auf die Wirklichkeit (es kann dies die Sicht eines Individums oder auch die Sicht einer ganzen Gruppe
von Individuen, beispielsweise einer ganzen Gesellschaft sein, oder gar sämtlicher Menschen überhaupt).
Anders ausgedrückt: Realität ist stets etwas nur durch unseren Verstand Konstruiertes — etwas nicht Wirkliches (siehe Wie real ist die Welt um uns herum?).
Nun weiß man aber:
- Einsteins Spezielle Relativitätstheorie zeigt: Jede Quantifizierung von Zeit ist subjektiv (genauer: abhängig vom gewählten Bezugssystem).
- Seine Allgemeine Relativitätstheorie aber — und insbesondere das sog.
Zwillingsparadoxon sowie seine den Physikern ja bekannte Lösung — zeigen:
Da sich das Alter eines Objekts aufgrund seiner Eigenzeit ergibt, ist Alter etwas Objektives, d.h. etwas, das man als wirklich (statt als nur real) anzusehen hat. Experimente im Labor mit schnell im Kreis bewegten, und damit beschleunigten Myonen bestätigen das:
In ihrem Experiment verglichen die Wissenschaftler zehntausend ruhende Teilchen im Labor mit zehntausend schnell bewegten Teilchen im Speicherring.
Die Messung zeigte, dass nach zwanzig Mikrosekunden kein einziges ruhendes Myon mehr vorhanden war, aber doch noch 8600 bewegte Myonen. Das Zwillingsparadoxon ist hier in spektakulärer Weise realisiert: Die meisten im Kreis bewegten Myonen existieren noch, wenn fast alle ruhenden schon zerfallen sind.
Quelle: http://www.weltderphysik.de/gebiete/theorie/albert-einstein-und-die-relativitaetstheorie/spezielle-relativitaetstheorie/
Siehe auch: Myonen und Spezielle Relativitätstheorie.
Auch die zentralen Ergebnisse der beiden Relativitätstheorien sollte man sich nochmals vor Augen geführt haben.
Nebenbei: Auf die Frage, » Was ist Zeit? « soll Einstein einmal geantwortet haben » Zeit ist, was man von der Uhr abliest «. Wie meine Argumentation oben zeigt, wissen wir jetzt, dass Einstein damit recht hatte — und das wirklich im buchstäblichen Sinne. Was er sagte, war ganz offenbar mehr als nur eine flapsige Bemerkung (wie klar auch immer ihm selbst das gewesen sein mag). Sein Gefühl dafür, was physikalisch richtig sein mag, war einzigartig.
Da wir jetzt also wissen, dass Zeit stets nur das subjektiv gefärbte Ergebnis einer Beobachtung von Eigenzeit ist, stellt sich die Frage, warum wir sie in unserem Alltagsleben dennoch dermaßen erfolgreich nutzen. Das aber liegt daran,
- dass in unserem Alltagsleben die Unterschiede zwischen Zeit und objektspezifischer Eigenzeit gering genug sind, dass man sie vernachlässigen kann
- bzw. dass wir gelernt haben, sie zu berücksichtigen in jedem Kontext, in dem sie nicht mehr ignoriert werden dürfen (beim GPS-System etwa).
Nebenbei noch: Was für das Paar Zeit und Eigenzeit richtig ist, gilt natürlich auch für das Paar Länge und Abstand: Länge ist das beobachterspezifisch subjektiv gefärbte Ergebnis einer Beobachtung von Abstand.
Mit der hier angesprochenen beobachterspezifischen Subjektivität ist natürlich stets das vom Beobachter gewählte Bezugssystem gemeint.
Natürlich lässt sich der eben beschriebene Sachverhalt aber auch über die Physik hinaus noch als richtig erkennen: Je spannender die Tätigkeit ist, die ein Mensch gerade ausübt, desto schneller wird ihm — seinem Gefühl nach — die Zeit vergehen. Ursache so entstandener Subjektivität ist dann (z.B.), wie oft jene Person sich gedrängt fühlt, auf eine Uhr zu sehen.
Nebenbei noch: Wie wir jetzt wissen, muss Einsteins Ausspruch
verstanden werden als
Letztlich ist jedes Objekt seine eigene Uhr.
Und tatsächlich schrieb Einstein (1905 in seinem Aufsatz Zur Elektrodynamik bewegter Körper): "Es könnte scheinen, dass alle die Definition der Zeit betreffenden Schwierigkeiten dadurch überwunden werden können, dass ich an Stelle der Zeit die Stellung des kleinen Zeigers meiner Uhr setze."
Da beschleunigte Objekte im Vergleich zu nicht beschleunigten aus der Sicht Dritter weniger schnell altern, sind die Entfernungen, die ein Mensch während seines Lebens im Prinzip überwinden kann, nur deswegen begrenzt, weil sein Organismus nur begrenzt hohe Beschleunigung auszuhalten im Stande ist.
Für Objekte, die sich mit Lichtgeschwindigkeit bewegen, gibt es keine Zeit.
Beitrag 2053-61
Kann man die SRT zu einer VSRT verallgemeinern?
Na ja, Eugen,
warum soll man ein Auseinanderdriften zweier Objekte nicht auch als r e l a t i v e Bewegung dieser Objekte zueinander sehen können?
Fakt ist doch:
Die ständige Änderung des Abstandes zweier Galaxien geht auf zwei Bewegungskomponenten zurück, die einfach nur unterschiedliche Ursache haben.
Einsteins SRT ist eine Theorie, die sich auf den Spezialfall v2 = 0 beschränkt.
Warum aber sollte sie nicht verallgemeinert werden können zu einer Theorie VSRT, die im Spezialfall v2 = 0 zu SRT wird?
Wahrscheinlich muss man dazu einfach nur in allen Formeln der SRT die Größe c (an der einen oder anderen Stelle, nicht an allen) durch c+v2 ersetzen.
Verifiziert habe ich das noch nicht — aber wir könnten es ja mal versuchen.
PS: Sollte es so eine Verallgemeinerung VSRT der SRT wirklich geben, kann sie nur anwendbar sein auf Situationen, in denen auch v2 < c ist (andernfalls nämlich würde von einer Galaxie G1 in Richtung der anderen ausgesandte Information jene ja niemals erreichen). Andererseits erfüllt der Fall v2 < c ja selbst schon alle Voraussetzungen der SRT — dann jedenfalls, wenn man die Expansionsgeschwindigkeit des Alls als unbeschleunigt annimmt (was über Zeiträume von weniger als 1 Mrd. Jahren ja eine ganz brauchbare Annäherung der Wirklichkeit darstellt).
Wenn wir jetzt annehmen, wir hätten Galaxien G1, G2, G3, derart, dass sich G2 genau in der Mitte zwischen G1 und G3 befindet, so ist die Geschwindigkeit v, mit der sich G1 und G3 auseinanderbewegen genau doppelt so groß wie die Geschwindigkeit, mit der G1 und G2 bzw. G2 und G3 sich voneinander entfernen.
Was würde das im Fall v/2 < c < v bedeuten?
Gruß,
grtgrt
Bauhof in 2053-52:
Das Größerwerden der Abstände zwischen den Galaxien ist weder eine relative Bewegung noch eine absolute Bewegung. Sie ist überhaupt keine Bewegung.
Es ist nur ein Auseinanderdriften aufgrund der Raumdehnung infolge der Universum-Expansion.
Na ja, Eugen,
warum soll man ein Auseinanderdriften zweier Objekte nicht auch als r e l a t i v e Bewegung dieser Objekte zueinander sehen können?
Fakt ist doch:
Die ständige Änderung des Abstandes zweier Galaxien geht auf zwei Bewegungskomponenten zurück, die einfach nur unterschiedliche Ursache haben.
- Bewegungskomponente B1 wird durch Gravitationspotential verursacht und führt zu einer Geschwindigkeitskomponente v1, die stets kleiner als c ist.
- Bewegungskomponente B2 wird durch Raumexpansion verursacht und führt zu einer Geschwindigkeitskomponente v2, die auch größer als c sein kann.
Einsteins SRT ist eine Theorie, die sich auf den Spezialfall v2 = 0 beschränkt.
Warum aber sollte sie nicht verallgemeinert werden können zu einer Theorie VSRT, die im Spezialfall v2 = 0 zu SRT wird?
Wahrscheinlich muss man dazu einfach nur in allen Formeln der SRT die Größe c (an der einen oder anderen Stelle, nicht an allen) durch c+v2 ersetzen.
Verifiziert habe ich das noch nicht — aber wir könnten es ja mal versuchen.
PS: Sollte es so eine Verallgemeinerung VSRT der SRT wirklich geben, kann sie nur anwendbar sein auf Situationen, in denen auch v2 < c ist (andernfalls nämlich würde von einer Galaxie G1 in Richtung der anderen ausgesandte Information jene ja niemals erreichen). Andererseits erfüllt der Fall v2 < c ja selbst schon alle Voraussetzungen der SRT — dann jedenfalls, wenn man die Expansionsgeschwindigkeit des Alls als unbeschleunigt annimmt (was über Zeiträume von weniger als 1 Mrd. Jahren ja eine ganz brauchbare Annäherung der Wirklichkeit darstellt).
Wenn wir jetzt annehmen, wir hätten Galaxien G1, G2, G3, derart, dass sich G2 genau in der Mitte zwischen G1 und G3 befindet, so ist die Geschwindigkeit v, mit der sich G1 und G3 auseinanderbewegen genau doppelt so groß wie die Geschwindigkeit, mit der G1 und G2 bzw. G2 und G3 sich voneinander entfernen.
Was würde das im Fall v/2 < c < v bedeuten?
Gruß,
grtgrt
Beitrag 2053-71
-
Könnte es bedeuten, dass der Begriff » Zeit aus unserer Sicht « überhaupt nur wohldefiniert sein kann in dem durch uns beobachtbaren Teil unseres Universums?
Grtgrt in 2053-61:
Sollte es so eine Verallgemeinerung VSRT der SRT wirklich geben, kann sie nur anwendbar sein auf Situationen, in denen auch v2 < c ist (andernfalls nämlich
würde von einer Galaxie G1 in Richtung der anderen ausgesandte Information jene ja niemals erreichen). Andererseits erfüllt der Fall v2 < c ja selbst schon alle Voraussetzungen der SRT — dann jedenfalls, wenn man die Expansionsgeschwindigkeit des Alls als unbeschleunigt annimmt (was über Zeiträume von weniger als 1 Mrd. Jahren ja eine ganz brauchbare Annäherung der Wirklichkeit darstellt).
Wenn wir jetzt annehmen, wir hätten Galaxien G1, G2, G3, derart, dass sich G2 genau in der Mitte zwischen G1 und G3 befindet, so ist die Geschwindigkeit v, mit
der sich G1 und G3 auseinanderbewegen genau doppelt so groß wie die Geschwindigkeit, mit der G1 und G2 bzw. G2 und G3 sich voneinander entfernen.
Was würde das im Fall v/2 < c < v bedeuten?
Beitrag 2053-103
Die einzigen Voraussetzungen der SRT
Hallo Eugen,
nimmt bitte mal an, wir hätten ein Gummiband, in das wir zwei Knoten gemacht haben.
Wenn ich jetzt das Gummiband an beiden Enden nehme und in die Länge ziehe, wird jeder sagen: "Die beiden Knoten b e w e g e n sich auseinander".
Du scheinst einen anderen Bewegungsbegriff zu haben (denn meinen Knoten geschieht ja nichts anderes als deinen Schnecken).
Mit anderen Worten: Du knüpfst den Begriff "sich bewegen" an eine bestimmte Ursache der Bewegung — andere Ursachen, so sagst Du, seien nicht erlaubt.
Die die SRT darstellenden Argumente sind aber doch gar nicht davon abhängig, welche U r s a c h e betrachtete Bewegungen haben. Kern der SRT ist doch einfach nur das Axiom, dass Information sich niemals schneller oder langsamer als mit Lichtgeschwindigkeit ausbreitet (und nichts sonst sich so schnell fortbewegt). Nur in Situationen, in denen die Information über eintretende Ereignisse zu unterschiedlichen Beobachtern hin unterschiedlich lange unterwegs ist, werden jene Beobachter unterschiedlichen Eindruck davon haben, wie lang eine Strecke oder ein Zeitabschnitt ist.
Sich beim Betrachten von Bewegungen auf ein bestimmtes Koordinatensystem zu beziehen, dient lediglich dem Zweck, Bewegung als solche feststellen zu können.
Mit anderen Worten: Die Welt und ihre Qualität ändern sich nicht in Abhängigkeit davon, ob wir sie gedanklich in ein bestimmtes Koordinatensystem einordnen — dem Koordinatensystem wird niemals mehr als nur gedankliche Existenz zukommen.
Wo die Geschwindigkeit v, mit der zwei Galaxien aufgrund der Expansion des Raumes auseinander driften, konstant und kleiner als c ist, wird die SRT ganz sicher auch für diese Art von Bewegung richtige Aussagen liefern.
Gruß, grtgrt
Bauhof in 2053-102:
Schnecke A verkündet nun:
"Keine hat sich bewegt, also kann nur eine höhere Macht die Entfernungen zwischen den Schnecken im Zeitraum (t’ – t) vergrößert haben!"
Schnecke C erwidert:
"Ich sehe es zwar, aber ich glaube es nicht! Wir haben uns trotzdem irgendwie bewegt!"
Hallo Eugen,
nimmt bitte mal an, wir hätten ein Gummiband, in das wir zwei Knoten gemacht haben.
Wenn ich jetzt das Gummiband an beiden Enden nehme und in die Länge ziehe, wird jeder sagen: "Die beiden Knoten b e w e g e n sich auseinander".
Du scheinst einen anderen Bewegungsbegriff zu haben (denn meinen Knoten geschieht ja nichts anderes als deinen Schnecken).
Mit anderen Worten: Du knüpfst den Begriff "sich bewegen" an eine bestimmte Ursache der Bewegung — andere Ursachen, so sagst Du, seien nicht erlaubt.
Die die SRT darstellenden Argumente sind aber doch gar nicht davon abhängig, welche U r s a c h e betrachtete Bewegungen haben. Kern der SRT ist doch einfach nur das Axiom, dass Information sich niemals schneller oder langsamer als mit Lichtgeschwindigkeit ausbreitet (und nichts sonst sich so schnell fortbewegt). Nur in Situationen, in denen die Information über eintretende Ereignisse zu unterschiedlichen Beobachtern hin unterschiedlich lange unterwegs ist, werden jene Beobachter unterschiedlichen Eindruck davon haben, wie lang eine Strecke oder ein Zeitabschnitt ist.
Sich beim Betrachten von Bewegungen auf ein bestimmtes Koordinatensystem zu beziehen, dient lediglich dem Zweck, Bewegung als solche feststellen zu können.
Mit anderen Worten: Die Welt und ihre Qualität ändern sich nicht in Abhängigkeit davon, ob wir sie gedanklich in ein bestimmtes Koordinatensystem einordnen — dem Koordinatensystem wird niemals mehr als nur gedankliche Existenz zukommen.
Wo die Geschwindigkeit v, mit der zwei Galaxien aufgrund der Expansion des Raumes auseinander driften, konstant und kleiner als c ist, wird die SRT ganz sicher auch für diese Art von Bewegung richtige Aussagen liefern.
Gruß, grtgrt
Beitrag 2053-105
-
Unter der Annahme, dass die Geschwindigkeit v, mit der zwei Galaxien sich aufgrund von was auch immer voneinander entfernen, konstant und kleiner als c ist, sind sämtliche Voraussetzungen der SRT erfüllt — genau deswegen werden in diesem Fall dann auch all ihre Schlußfolgerungen zutreffend sein.
Bauhof in 2053-104:
Denke erst mal darüber nach, bevor du immer so schnell antwortest.
Unter der Annahme, dass die Geschwindigkeit v, mit der zwei Galaxien sich aufgrund von was auch immer voneinander entfernen, konstant und kleiner als c ist, sind sämtliche Voraussetzungen der SRT erfüllt — genau deswegen werden in diesem Fall dann auch all ihre Schlußfolgerungen zutreffend sein.
Beitrag 2051-6
-
Es wird gesagt, die SRT gelte dort näherungsweise, wo die Gravitation vernachlässigbar sei – im intergalaktischen Raum fernab von Galaxien oder lokal begrenzt.
Ich wage zu behaupten, sie gilt dort exakt, wo keine Gravitationspotentialdifferenzen durchschritten werden.
Also entlang der Erdoberfläche, aber nicht senkrecht zu ihr.
mfg okotombrok�
Ich wage zu behaupten, sie gilt dort exakt, wo keine Gravitationspotentialdifferenzen durchschritten werden.
Also entlang der Erdoberfläche, aber nicht senkrecht zu ihr.
mfg okotombrok�
Beitrag 2016-34
Minkowskis Integration der Konzepte Zeit und Raum erhält ihr unterschiedliches Wesen
Sie sind doch voneinander getrennt, denn:
Da sich selbst nach Minkowskis Theorie Zeit nicht in Raum (und Raum auch nicht in Zeit) verwandeln kann, sind auch in seiner Theorie beide Konzepte ganz klar auseinandergehalten. Er selbst präzisiert das, indem er sagt (FOCUS Online, der Artikel, auf den auch Du dich beziehst):
So — und NUR so — ist seine Aussage "Die Tendenz ist eine radikale. Von Stund’ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken, und nur noch eine Art Union der beiden soll Selbstständigkeit bewahren." zu verstehen. Gemeint war also nur: Wir haben jetzt e i n Modell, in das Raum u n d Zeit sich gleichermaßen gut einfügen.
Ich bleibe also dabei:
Die Relativitätstheorie — Einstein und Minkowski — formalisieren die enge Beziehung zwischen Zeit und Raum,
können aber dennoch nicht wegdiskutieren, dass beide unterschiedliches Wesen haben.
Henry aus 2016-33:Grtgrt aus 2016-32:
Hi Henry,
sehr viele Leute, so auch Du, sagen, die Raumzeit würde den Raum von der Zeit nicht trennen.
Das hat mir nie so richtig eingeleuchtet, denn auch dort ist ja der Raum 3-dimensional, die Zeit aber 1-dimensional.
Warum also wagst du zu behaupten, sie seien in der ART — als zwei unterschiedliche Konzepte — nicht klar voneinander getrennt?
Gruß, grtgrt
Die Raumzeit ist vierdimensional. Ich "wage" überhaupt nicht zu behaupten.
Sie s i n d in der ART nicht als zwei unterschiedliche Konzepte klar voneinander getrennt.
Sie sind doch voneinander getrennt, denn:
Da sich selbst nach Minkowskis Theorie Zeit nicht in Raum (und Raum auch nicht in Zeit) verwandeln kann, sind auch in seiner Theorie beide Konzepte ganz klar auseinandergehalten. Er selbst präzisiert das, indem er sagt (FOCUS Online, der Artikel, auf den auch Du dich beziehst):
Zitat:
Mit Minkowskis Worten: "Die dreidimensionale Geometrie wird zu einem Kapitel in der vierdimensionalen Physik." Diese Minkowski-Raumzeit lässt sich entweder als ein vierdimensionaler mathematischer Raum interpretieren, der die Zeitentwicklung der dreidimensionalen Welt repräsentiert, oder als mathematisches Modell einer vierdimensionalen Welt, in der die Zeit die vierte Dimension ist....
So — und NUR so — ist seine Aussage "Die Tendenz ist eine radikale. Von Stund’ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken, und nur noch eine Art Union der beiden soll Selbstständigkeit bewahren." zu verstehen. Gemeint war also nur: Wir haben jetzt e i n Modell, in das Raum u n d Zeit sich gleichermaßen gut einfügen.
Ich bleibe also dabei:
können aber dennoch nicht wegdiskutieren, dass beide unterschiedliches Wesen haben.
Beitrag 2016-35
-
Interessant ist auch:
Die beiden Hauptvertreter der Theorie der Schleifen-Quantengravitation — Lee Smolin und Carlo Rovelli — sind sich nicht einig, welcher Natur die Zeit denn nun eigentlich ist:
Interessant ist auch:
Die beiden Hauptvertreter der Theorie der Schleifen-Quantengravitation — Lee Smolin und Carlo Rovelli — sind sich nicht einig, welcher Natur die Zeit denn nun eigentlich ist:
- Smolin denkt, sie sei wesentlich und müsse Teil der Theorie sein,
- Rovelli aber tendiert dazu, sie für eine nur gedanklich existierende Hilfskonstruktion zu halten (und will sie deswegen nicht als Teil der Theorie sehen).
Beitrag 2016-37
-
Wer nicht weiß, was "unteilbar" in diesem Sinne bedeutet, weiß dann also gar nichts.
Ich ziehe es vor, zu klären, was "unteilbar" in diesem Sinne heißt, und komme so zum Schluß, dass auch Physiker darunter nicht mehr verstehen, als dass die Zeit eine der Dimensionen der Raumzeit ist (im mathematischen Sinne des Begriffs der "Dimension"), was weder mehr noch weniger bedeutet, als dass man ein und denselben Ort zu verschiedener Zeit betrachten kann.
Henry aus 2016-36:Ich halte mich an die Übereinkunft der Physikerzunft, die die Raumzeit für unteilbar nimmt (wenn sie sich auf die Relativitätstheorie bezieht).
Wer nicht weiß, was "unteilbar" in diesem Sinne bedeutet, weiß dann also gar nichts.
Ich ziehe es vor, zu klären, was "unteilbar" in diesem Sinne heißt, und komme so zum Schluß, dass auch Physiker darunter nicht mehr verstehen, als dass die Zeit eine der Dimensionen der Raumzeit ist (im mathematischen Sinne des Begriffs der "Dimension"), was weder mehr noch weniger bedeutet, als dass man ein und denselben Ort zu verschiedener Zeit betrachten kann.
Beitrag 1991-1
Kernaussagen der Speziellen Relativitätstheorie
Hallo zusammen,
bitte hier keine Beiträge einstellen!
Warum? Es soll nur der erste Beitrag hier verbleiben, den ich immer auf den neuesten Stand nach Absprache mit Zara.t. bringe. Er soll eine Wissensplattform zur SRT für alle werden, damit jeder darauf zurückgreifen kann, wenn Fragen entstehen. Hier eingehende Beiträge werden weder von mir noch von Zara.t. beantwortet.
Wenn ihr darüber diskutieren möchtet, dann bitte im Thread Basics spezielle Relativitätstheorie! Vielen Dank im Voraus.
M.f.G. Eugen Bauhof
Forenteilnehmer, deren Beiträge bis jetzt hier eingebracht wurden (in alphabetischer Reihenfolge):
Bauhof, Grtgrt, Henry, Okotombrok, Zara.t.
Themen, die demnächst in den SRT-Basics diskutiert werden sollen:
(A) Begriff des Beobachtens.
(B) Maxwellsche Gleichungen.
(C) E = mc2.
(D) Die Lorentz-Transformationen, hergeleitet allein aus dem Relativitätsprinzip.
(E) Transformationen, die das Linienelement ds2 = (c dt)2 - dx2 - dy2 - dz2 invariant lassen.
Arbeitsplattform SRT
Inertialsysteme
1. Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig. Alle Inertialsysteme bewegen sich relativ zueinander mit einer Geschwindigkeit v<c.
2. Sich drehende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme.
3. Auch gleichförmig beschleunigte Systeme sind keine Inertialsysteme. Eine gleichförmige Beschleunigung ist keine gleichförmige Bewegung und somit nicht der Ruhe äquivalent.
4. Ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, hat keine Ruhemasse. Deshalb gibt es kein Inertialsystem, in dem Photonen in Ruhe wären.
5. Ein System, in dem sich jeder kräftefreie Körper gleichförmig geradlinig bewegt, wird als Inertialsystem bezeichnet.
6. Das Zusammentreffen von Kräftefreiheit und gleichförmiger Geradlinigkeit sämtlicher Bewegungen gibt es nur in Inertialsystemen.
7. Es kann kein Inertialsystem geben, das sich relativ zu einem zweiten Inertialsystem mit c bewegt. Grund: alle lichtartigen Weltlinien haben die Länge Null.
8. Wenn ein Lichtstrahl im Koordinatenursprung O(0,0,0) startet. dann gilt:
S2 = (ct)2 - x2 - y2 - z2 ; für Licht gilt: x2 + y2 + z2 = (ct)2 ==> S2 = (ct)2 - (ct)2 = 0; S = 0
Wichtig: S ist für alle (also auch für die nicht lichtartigen) Weltlinien invariant unter Lorentztransformationen. Das heißt: die Eigenzeit eines Systems ist eine absolute Größe, sie ist die Zeit, die eine mit diesem System fest verbundene Borduhr anzeigt.
Relativitätsprinzip
1. Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen werden.
2. Alle Inertialsysteme sind gleichberechtigt, wenn es gilt Naturgesetze zu formulieren. Naturgesetze müssen kovariant formuliert werden können.
3. Alle Beobachter, die sich mit gleichförmiger Geschwindigkeit relativ zueinander bewegen, sind gleichermaßen zu der Behauptung berechtigt, sie befinden sich in Ruhe.
Absolute Ruhe
Die Physik kennt keine absolute Ruhe. Die Gesetze der Physik lauten in allen Inertialsystemen gleich und zeichnen keines aus (Relativitätsprinzip). Es gibt nur relative Ruhe, Ruhe in bezug auf ein spezielles Inertialsystem, das momentane Ruhsystem.
Absolutgeschwindigkeit
Mit keinem Experiment kann eine Absolutgeschwindigkeit eines Inertialsystems bestimmt werden; kein Experiment lässt die Unterscheidung von Ruhe und gleichförmiger Bewegung zu. Damit war auch das vor Einstein der als absolut ruhendes Lichtwellen-Trägermedium angesehene "Lichtäther" gegenstandslos, den "Lichtäther" gibt es nicht.
Beobachten
Unter Beobachten versteht man die Feststellung der Koordinaten von Ereignissen in einem Inertialsystem. Wenn man das wirkliche Beobachten meint, muss man die endliche Laufzeit des Lichtsignals vom Gegenstand zum Betrachter berücksichtigen.
Den Begriff des Beobachtens möchte Zara.t. noch diskutieren. Er ist von zentraler Wichtigkeit um das Denken und die Arbeitsweise Einsteins zu verstehen.
Lichtgeschwindigkeit
1. Die Lichtgeschwindigkeit ist eine physikalische Naturkonstante und hat einen exakt definierten Wert.
2. Man kann c=1 setzen. Um hier im Forum Missverständnisse zu vermeiden, wird folgendes vereinbart:
Lichtgeschwindigkeit im Vakuum (im SI-System): c = 299 792 458 m/s
3. Die Existenz einer invarianten Grenzgeschwindigkeit folgt aus dem Relativitätsprinzip. Der Wert dieser Grenzgeschwindigkeit wird von den Maxwellschen Gleichungen festgelegt und durch alle Messungen bisher bestätigt.
4. Aus den Maxwellschen Gleichungen ergibt sich die Ausbreitungsgeschwindigkeit c elektromagnetischer Wellen aus zwei experimentell herausgefundenen Konstanten:
c = 1/sqrt(ε0 • ε0)
ε0 = magnetische Feldkonstante.
ε0 = elektrische Feldkonstante.
Eigenzeit einer Uhr
Die Eigenzeit einer Uhr entspricht immer der Länge ihrer Weltlinie.
Länge der Weltlinie eines bewegten Objekts
Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit... Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Maxwellsche Gleichungen
Die Maxwellschen Gleichungen sagen in einfachen Worten: Die Änderung eines elektrischen Feldes induziert ein magnetisches Feld, die Änderung des magnetischen Feldes induziert ein elektrisches Feld, das sich ändernde elektische Feld induziert ein Magnetfeld, usw....dieser ständige Wechsel breitet sich wellenförmig mit c (im Vakuum) aus. Die Maxwellschen Gleichungen sind früher als die SRT unabhängig von der SRT entstanden. An ihrem Beispiel könnten wir zeigen, was eine kovariante Formulierung ist. So wie Maxwell seine Gleichungen formulierte, waren sie nämlich noch nicht kovariant. Man kann ihnen aber eine kovariante Form verpassen.
Energie-Impuls-Beziehung
Die Energie-Impuls-Beziehung ist eine invariante Größe:
E2 – (pc)2 = (mc2)2 || = constant
E..................Gesamtenergie, sie ist bezugssystemabhängig.
p...................Impuls, er ist bezugssystemabhängig.
mc2:=E0.......Ruheenergie sie ist bezugssystemunabhängig.
Nachdem die Ruheenergie bezugssystemunabhängig ist, ist auch die Masse m invariant.
SRT-Glossar
Äther
Ein Medium, in dem sich Licht und andere elektromagnetische Wellen fortpflanzen sollten. Diese Vorstellung wurde, vor allem nach der Entdeckung der Speziellen Relativitätstheorie, durch eine Feldbeschreibung ersetzt, nach der sich elektromagnetische Wellen auch ohne jedes Medium im leeren Raum fortpflanzen können. Die Vorstellung vom Äther wurde durch die Relativitätstheorie widerlegt.
Beobachter
Idealisierte Person oder Apparatur, oft hypothetischer Natur, die relevante Eigenschaften eines physikalischen Systems misst. Jeder Beobachter, der sich inertial bewegt, darf annehmen, dass er selbst in Ruhe sei. Er beobachtet lediglich, dass alle anderen Beobachter sich relativ zu ihm bewegen oder in Ruhe sind. Mehr kann er nicht beobachten, insbesondere kann er keine Eigenbewegung aus den Bewegungen anderer ableiten. Für ihn sieht es so aus, als würde er ruhen und alle anderen Beobachter bewegen sich.
Beschleuniger
Ein Instrument, das die Geschwindigkeit, und damit die Energie, geladener Teilchen erhöht. Beschleunigt werden können stabile Teilchen wie Elektron, Proton und Ionen.
Beschleunigung
Eine Veränderung der Geschwindigkeit, das heißt des Geschwindigkeitsbetrags und/oder der Bewegungsrichtung eines Objekts.
Bezugssystem
Die räumliche Beschreibung von Vorgängen braucht ein Bezugssystem (Koordinatensystem, Koordinaten) In einem Bezugssystem kann man die Bewegung eines Körpers beschreiben, ebenso aber auch die Bewegung eines anderen Bezugsystems, z. B. eine gradlinig gleichförmige Bewegung eines Bezugssystems in einem anderen, oder auch eine Drehung, eine krummlinige Bewegung oder eine beliebige Beschleunigung. Die Spezielle Relativitätstheorie diskutiert die Frage, wie sich zwei Beschreibungen desselben Vorgangs zueinander verhalten, die zu Bezugssystemen gehören die gegeneinander gleichförmig bewegt sind. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme.
Dilatation
Das Auseinanderziehen, die Verlängerung. Hier gebraucht im Zusammenhang mit Zeitdilatation, d.h. die Verlängerung der Zeiten in einem bewegten System gemäß der Speziellen Relativitätstheorie.
Doppler-Effekt-Verschiebung
Verschiebung der Spektrallinien einer Strahlung durch die Bewegung ihrer Quelle relativ zur Sichtlinie. Annäherung verursacht Blauverschiebung, Entfernung Rotverschiebung.
Eigenzeit
Eigenzeit ist die Zeit, gemessen von einer Uhr, welche die Bewegung eines Beobachters mitmacht. Uhren in relativer Bewegung zu einem Beobachter messen, dass seine und die Eigenzeit verschieden schnell vergehen. Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit. Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Elektrodynamik
Theorie der elektrischen und magnetischen Erscheinungen, zusammengefasst in der einheitlichen Elektrodynamik am Ende des 19. Jahrhunderts durch Maxwell. Dazu gehört vor allem die Theorie der elektromagnetischen Wellen, wie z. b. Radiowellen, Licht oder Gammastrahlen.
Elektromagnetische Welle
Eine wellenartige Störung in einem elektromagnetischen Feld. Alle diese Wellen breiten sich mit Lichtgeschwindigkeit aus. Sichtbares Licht, Röntgenstrahlen, Mikrowellen und Infrarotstrahlung sind Beispiele dafür.
Energie
Physikalische Grundgroße, für die ein strenger Erhaltungssatz gilt. Sie kann verschiedene Formen annehmen, z. B. die potentielle Energie eines im Schwerefeld hochgehobenen Gewichts, die kinetische Energie eines bewegten Körpers, die Wärmeenergie, in die schließlich jede Energie anderer Formen übergeht, oder die als Masse vorhandene Energie gemäß der Speziellen Relativitätstheorie. ("Trägheit der Energie")
Ereignis
Ein Weltpunkt in der Raumzeit. Beschrieben durch vier Koordinaten: {x, y, z. t}.
Frequenz
Die Zahl vollständiger Wellenzyklen, die eine Welle pro Zeiteinheit durchläuft.
Grobes Missverständnis der SRT.
Etliche Kritiker der SRT in den letzten 100 Jahren glaubten, die relativistische Zeitdilatation sei ein rein "perspektivischer" Beobachtungs-Effekt und allein durch die Lichtlaufzeiten zum Beobachter zu erklären. Ein ganz grobes Missverständnis der SRT.
Geschwindigkeit
Der Geschwindigkeitsbetrag und die Bewegungsrichtung eines Objekts, zu einer Größe zusammengefasst. Die Geschwindigkeit ist differentiell definiert als Ortsänderung pro Zeiteinheit.: v = dx/dt. Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle, deren Radius sich mit 299 752 458 m/sec vergrößert. Ihr Durchmesser aber vergrößert sich doppelt so schnell. Das ist kein Widerspruch zur SRT, da die Rate, mit der sich ein Abstand vergrößert, nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann. Diese Vergrößerung des Durchmessers kann nicht mit der Einsteinschen Geschwindigkeitsadditions-Formel berechnet werden, weil es sich bei der Verdoppelung des Durchmessers nicht um eine Geschwindigkeit im Sinne der SRT handelt.
Gleichzeitigkeit
In der klassischen Mechanik ist die Gleichzeitigkeit von Ereignissen unabhängig von jedem Bewegungszustand und von der Entfernung definiert. In der speziellen Relativitätstheorie hängt die Definition der Gleichzeitigkeit von der Relativ-Geschwindigkeit und von der Entfernung ab (Einsteins Relativität der Gleichzeitigkeit).
Gleichzeitigkeits-Definition von Einstein
"Die für A und B gemeinsame Zeit kann so definiert werden, indem man durch Definition festsetzt, dass die Zeit, welche das Licht braucht, um von A nach B zu gelangen, gleich ist der Zeit, welche es braucht, um von B nach A zu gelangen."
Für entfernte Punkte kann man zu einer Gleichzeitigkeits-Definition also überhaupt nur gelangen auf dem Wege eines konstruktiven Postulats, in dem gefordert wird, dass die Ausbreitung des Lichtes, gemessen in der noch zu definierenden gemeinsamen Zeit, ein Vorgang mit konstanter Geschwindigkeit ist. Dieses Postulat ist entscheidend an der Konstruktion des Begriffs der gemeinsamen Zeit beteiligt.
Ideale Uhren.
Zur Herleitung der Theorien (der SRT und der ART) legt man sogenannte "ideale" Uhren zugrunde. So eine ideale Uhr wird realisiert durch Atomuhren. Reale Experimente, welche die SRT belegen, werden mit den Taktraten von Atomuhren durchgeführt
Inertialsystem.
Ein Inertialsystem ist ein Bezugssystem, in dem sich kräftefreie Körper geradlinig gleichförmig bewegen. Das bedeutet, dass es sich bei einem Inertialsystem um ein nicht rotierendes und nicht beschleunigtes Bezugssystem handelt. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme. Somit bewegen sich Körper, auf die keine Kräfte wirken, in allen Inertialsystemen auf Geraden. Eine gleichförmige Rotationsbewegung wäre demzufolge nichtinertial. Jeder nichtrotierende Beobachter, der sich gleichförmig und unbeschleunigt bewegt, befindet sich in einem Inertialsystem. Auf ihn wirken keine Kräfte.
Es gibt kein ausgezeichnetes Inertialsystem, von dem man behaupten könnte, es sei absolut ruhend. Es gibt keinen Punkt im Universum, von dem man sagen könnte, das sei allein der "absolut ruhende Pol", auf dem man jede andere Bewegung beziehen könnte. Insbesondere gibt es auch keinen "absoluten Raum", auf dem man alle Bewegungen beziehen könnte. Sowohl in der klassischen Mechanik wie in der Speziellen Relativitätstheorie sind alle Inertialsysteme für die Beschreibung gleichberechtigt.
Isotropie
Unabhängigkeit von Richtung oder Winkel. In einem isotropen Universum sind sämtliche messbaren Größen in allen Richtungen gleich.
Invarianz
Die Unveränderlichkeit bestimmter Größen oder Beziehungen, auch wenn andere Charakteristika transformiert werden. Invarianz-Überlegungen der Physik beziehen sich gewöhnlich auf die Invarianz von Größen gegenüber Transformationsgruppen.
Invarianz der Lichtgeschwindigkeit.
Unter der Invarianz der der Lichtgeschwindigkeit versteht man z.B. folgendes: Für das Licht wird immer die gleiche Geschwindigkeit gemessen, unabhägig davon, ob sich die Lichtquelle auf uns zu- oder von uns fortbewegt. Das sehen alle Beobachter so, gleichgültig, ob sie auf der Lichtquelle sitzen oder ob sie sich außerhalb befinden und die Lichtquelle als bewegt wahrnehmen. Daraus folgt: Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich groß.
Kinematik der Relativitätstheorie
Die Grundlagen der Relativitätstheorie können durch geometrische Intuition erschlossen werden. Die Kinematik der Relativitätstheorie kann daher als die Geometrie der Raumzeit-Union angesehen werden.
Kinetische Energie
ist die mit der Bewegung verknüpfte Energie; sie ist gleich der Arbeit, die geleistet werden muss, um einen Körper der Masse m aus dem Ruhezustand in einen Bewegungszustand mit der Geschwindigkeit v zu bringen. Sie beträgt in der klassischen Mechanik 1/2•m•v2.
Konstanz der Lichtgeschwindigkeit
Darunter versteht man die Unabhängigkeit von der Ausbreitungsrichtung und die Unveränderlichkeit ihrer Größe bei Zusammensetzung.
Unabhängigkeit von der Ausbreitungsrichtung heißt zum Beispiel: Wenn ein Lichtstrahl senkrecht auf eine Spiegelfläche mit der Geschwindigkeit v=c trifft, dann hat auch der reflektierte Strahl die Geschwindigkeit v=c. Strahlen, die nicht senkrecht auftreffen, werden ebenfalls mit der Geschwindigkeit v=c reflektiert.
Kovariant
Die Beschreibung eines physikalischen Systems ist kovariant, wenn bei einer Transformation des Systems die transformierte Beschreibung des transformierten Systems dieselben Ergebnisse liefert wie die ursprüngliche Beschreibung des ursprünglichen Systems.
Lichtlaufzeiten.
Mit den Lichtlaufzeiten zum Beobachter sind die relativistischen Effekte nicht erklärbar. Das schließt nicht aus, dass man zum besseren Verstehen Gedankenexperimente macht, in denen die Lichtlaufzeiten mit einbezogen werden.
Lichtuhr
Eine hypothetische Uhr, welche die verstrichene Zeit misst, indem sie zählt, wie viele vollständige Rundreisen ein einzelnes Photon zwischen zwei Spiegeln zurücklegt.
Lorentz-Kontraktion
Besonderheit, die sich aus der speziellen Relativitätstheorie ergibt. Ein bewegtes Objekt erscheint einem ruhenden Beobachter, der dessen Länge misst, in Richtung der Bewegung verkürzt.
Minkowski-Raumzeit
Minkowski erkannte, dass die Kinematik der SRT graphisch darstellbar wird, wenn man neben den altbekannten kartesischen Koordinatenachsen x, y, z noch die vierte Achse ict einführt und sich bei der Veranschaulichung relativistischer Raum-Zeit-Verhältnisse auf jeweils zwei Achsen, typischerweise die Achsen x und ict, beschränkt. Für die Abstände zwischen Weltpunkten, die jetzt Raum- und Zeitkoordinaten hatten, galt die alte euklidische Regel quadrierter Koordinaten-Differenzen, allerdings mit einem durch i2 = –1 veränderten Vorzeichen des zeitlichen Anteils:
ds2 = dx2 + dy2 + dz2 + d(ict)2
Die Lorentztransformationen konnten dann als Drehung in dieser vierdimensionalen Raumzeit verstanden werden, bei der diese Größe ds2 invariant blieb ebenso wie bei Drehung im dreidimensionalen Raum der dreidimensionale Abstand zweier Körper unverändert bleibt. Effekte wie die Lorentzkontraktion und die Zeitdilatation konnten nun als durch Projektion von Längen- und Zeitanteil von eigentlich längen- und zeitbehafteten Größen auf zueinander um den Winkel ß = arctan(v/c) gedrehte Koordinatenachsen anschaulich interpretiert werden.
Mittelpunkt im Universum.
Im Universum ist kein Ort feststellbar, der als Mittelpunkt im Universum bezeichnet werden könnte.
Newtonsche Bewegungsgesetze
Gesetze, welche die Bewegung von Körpern unter Kräfteeinfluss beschreiben, wobei sie voraussetzen, dass Raum und Zeit absolut und unwandelbar sind. Diese Gesetze galten unverändert, bis Einstein die spezielle Relativitätstheorie entdeckt hatte, die zeigt, dass die Newtonsche Theorie nur eine Näherung für den Grenzfall kleinerer Geschwindigkeiten ist.
Photon
Kleinstes Paket des elektromagnetischen Felds. Botenteilchen der elektromagnetischen Kraft. Kleinstes Lichtpaket.
Pseudoeuklidische Geometrie
Während in einem euklidischen Raum das Quadrat des Abstandes zweier verschiedener Punkte P1 und P2 stets größer als Null ist, kann es in der Minkowski-Welt auch kleiner oder gleich Null sein. Die Raumzeit-Union der Relativitätstheorie besitzt also keine euklidische Maßbestimmung. Vielmehr ist die Maßbestimmung die vierdimensionale Verallgemeinerung der pseudo-euklidischen Geometrie. Dies ist der mathematische Ausdruck dafür, dass die Zeitkoordinate eine andere Qualität als die 3 Raumkoordinaten besitzt.
Raum und Zeit als untrennbare Einheit.
Man kann die SRT nicht auf der Grundlage der klassischen Betrachtung mit Trennung von Raum und Zeit verstehen. Man kann die SRT erst dann verstehen, wenn man Raum und Zeit als untrennbare Einheit ansieht.
Raumzeit
Die drei physikalischen Dimensionen des Raums werden mit der Zeit, die als vierte Dimension aufgefasst wird, verknüpft und ergeben so das Raum-Zeit-Kontinuum, das den grundlegenden Rahmen in der Relativitätstheorie darstellt.
Relativgeschwindigkeit.
Jede Geschwindigkeit (eines Körpers oder eines Inertialsystems) ist immer nur eine Relativgeschwindigkeit.
Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in Bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
Relativität der Gleichzeitigkeit.
Das ist die erste Konsequenz der Konstanz der Lichtgeschwindigkeit. Einstein argumentierte etwa wie folgt: Auch die Zeit ist relativ. Es gibt keine absolute Zeit, die für alle Inertialsysteme gültig ist. In jedem Inertialsystem läuft die Zeit anders ab, abhängig davon, wie schnell sich die Inertialsysteme relativ zueinander bewegen. Und das ist ein totaler Umsturz unseres Weltbildes, weil seit Newton die Zeit "überall gleich verfließt". Und genau das tut sie nicht.
Was für einen Beobachter gleichzeitig ist, ist für einen anderen bewegten Beobachter nicht gleichzeitig. Ob zwei räumlich getrennt liegende Ereignisse gleichzeitig sind oder nicht, kann nicht dadurch entschieden werden, dass man mit Hilfe einer Messung die Gleichzeitigkeit zweier Ereignisse feststellen könnte. Der Gleichzeitigkeits-Begriff getrennt liegender Ereignisse erlangt erst durch eine Definition seine Bestimmtheit. Gleichzeitigkeit ist objektiv unbestimmt.
Relativitätsprinzip
Zentraler Begriff der Relativitätstheorie, nach der die physikalischen Gesetze für alle Beobachter, die mit konstanter Geschwindigkeit relativ zueinander bewegt sind, die gleiche Form haben; daher ist jeder dieser Beobachter gleichermaßen zu der Behauptung berechtigt, er befinde sich in Ruhe. Dieses Prinzip wird in der allgemeinen Relativitätstheorie zum Äquivalenzprinzip erweitert. Bereits in der Newtonschen Mechanik waren alle Inertialsysteme gleichberechtigt. Die Newtonschen Axiome der Mechanik zeichnen kein Inertialsystem gegenüber dem anderen aus. Der Übergang von einem Inertialsystem in ein anderes Inertialsystem wird in der Newtonschen Mechanik durch eine Galilei-Transformation vollzogen.
Relativistischer Dopplereffekt
Der relativistische Dopplereffekt hängt nur von der Relativgeschwindigkeit von Sender und Empfänger ab.
Ruheenergie
ist die aus der Beziehung E0 = mc2 berechnete Energie , wobei m die Masse des Teilchens und c die Lichtgeschwindigkeit ist. Die Ruhenergie wird nur dann vollständig freigesetzt, wenn ein Teilchen mit seinem Antiteilchen zerstrahlt.
Ruhesystem.
Man kann sich als Beobachter in jedes beliebige Inertialsystem gedanklich hineinsetzen kann, um dieses Inertialsystem dann zum Ruhesystem zu erklären.
Spezielle Relativitätstheorie
Einsteins Gesetze von Raum und Zeit in Abwesenheit von Gravitation.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
Teilchenbeschleuniger
Anlage, die Teilchen fast auf Lichtgeschwindigkeit beschleunigt und sie dann mit anderen Teilchen zusammenstoßen lässt, um ihren materiellen Aufbau zu ermitteln.
Vektorraum
In der Mathematik eine Gesamtheit von Vektoren, d.h. Objekten, die sich addieren und mit Zahlen multiplizieren lassen. Vektorräume unterscheiden sich nach der Art dieser Zahlen (z. b. reelle oder komplexe Zahlen) und nach ihrer Dimensionszahl. Zum Beispiel bilden die möglichen Geschwindigkeiten im Raum einen dreidimensionalen reellen Vektorraum.
Vierdimensionaler Abstand zwischen zwei Ereignissen.
Für alle inertialen Beobachter ist der vierdimensionale Abstand zwischen zwei Ereignissen in der Raumzeit verbindlich. Alle messen den gleichen Wert. Man sagt, dieser Abstand ist das "Raumzeit-Intervall" und dieses ist invariant für alle Beobachter. Wenn man die zwei Raumdimensionen y und z weglässt und nur eine Raumdimension x und die Zeitdimension t betrachtet, dann ergibt sich das Raumzeit-Intervall s2 zwischen zwei Ereignissen für zwei verschiedene Systeme wie folgt:
s2 = (ct')2 - (x')2 = (ct)2 - (x)2.
Wellenlänge
Elektromagnetische Strahlung wird durch ihre Wellenlänge oder ihre Frequenz charakterisiert, deren Produkt gleich der Lichtgeschwindigkeit ist. Die Wellenlänge ist die Entfernung zwischen aufeinanderfolgenden Wellenfronten, und die Frequenz ist die Zahl der Wellenfronten, die an einen gegebenen Punkt in einer Sekunde vorbeilaufen. Im sichtbaren Bereich hat das Licht eine Wellenlänge von 400 bis 700 Nanometer und eine Frequenz von 7 x 1014 bis 4 X 1014 Hertz.
Weltlinie
Eine Abfolge von Weltpunkten.
Weltpunkt
Ein Ort in der Raumzeit. Er ist bestimmt durch vier Koordinaten: {x, y, z, t}
Zwillingsparadoxon.
Gegen Einsteins Zwillingsexperiment wird meist mit der Symmetrie der Zeitdilatation argumentiert:
Wenn Zwilling B einerseits die Uhr von Zwilling A langsamer gehen sieht, dann muss umgekehrt doch Zwilling A auch die Uhr von B langsamer gehen sehen. Das ist zwar richtig, gilt aber nur, solange sich Zwilling A und B jeweils in einem Inertialsystem bewegen. Doch Zwilling B muss umkehren, um zu A zurückkehren zu können, d. h., er beschleunigt und befindet sich daher nicht in einem Inertialsystem, im Gegensatz zu B.
Diese Antwort wiederum hat dazu geführt, dass oftmals die Beschleunigungsphasen von B für die Verjüngung verantwortlich gemacht werden. Aber auch das ist nicht richtig, wie sich leicht zeigen lässt, indem man aus dem Zwillingsparadoxon ein Drillingsparadoxon macht. In der nachstehenden Skizze sind die Weltlinien der Drillinge A, B und C dargestellt, wobei C identische Beschleunigungsphasen (gekrümmte Kurvenstücke, durchgezogen gezeichnet) durchläuft, allerdings ist seine Reise kürzer.
Nach Zusammenkunft aller drei ist A älter als C und C älter als B. Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden. Es ist die physikalische Geometrie der relativistischen Raumzeit: Der Weg von B ist kürzer als der von C, und dieser wiederum ist kürzer als der Weg von A.
Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
1. Die Symmetrie der Zeitdilatation wird gebrochen, sobald der reisende Zwilling umkehrt.
2. Die Umkehr ist gleichbedeutend mit einem Inertialsystemwechsel.
3. Der Inertialsystemwechsel bei der Umkehr lässt die auf seiner Reise erarbeitete Zeitdilatation des reisenden Zwillings manifest werden.
4. Die verflossene Eigenzeit, die der jeweilige Zwilling auf seiner Uhr abliest, entspricht der jeweiligen Länge der Weltlinie im Minkowski-Raum.
5. Die Beschleunigungsphasen des reisenden Zwillings sind nicht die Ursache der Zeitdilatation. Man kann die Beschleunigungsphasen durch ein Differenzexperiment zum Verschwinden bringen. Die Zeitdilatation tritt dann trotzdem auf. Die Zeitdilatation ist im wesentlichen abhängig von der Reisedauer und der Reisegeschwindigkeit des reisenden Zwillings.
6. Manche meinen, dass nur die ART das scheinbare Paradoxon auflösen könnte, weil Beschleunigungen im Spiel sind. Mal ganz abgesehen davon, dass man mit der SRT auch Beschleunigungen beschreiben kann, ist die ART zu Auflösung des Zwillingsparadoxons nicht notwendig. Es kann allein mit Mitteln der SRT gelöst werden. Die ART wird nur dann benötigt, wenn die Gravitation ins Spiel kommt.
Herleitung der Lorentz-Transformationen mit Hilfe einer Koordinatensystemdrehung im Minkowski-Raum.
Zunächst wird die gewöhnliche Koordinatentransformation im euklidischen Raum in Skizze 1 dargestellt, so wie sie in jeder Formelsammlung zu finden ist:
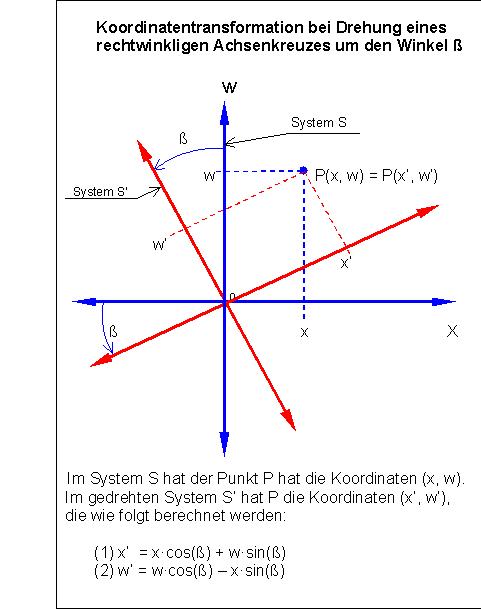
Skizze 1
Der Mathematiker Hermann Minkowski Minkowski ging von der Invarianz des Linienelementes aus und suchte allgemeine Transformationsgleichungen, die dies gewährleisten. Er hat dabei herausgefunden, dass allgemein jede Transformation zwischen relativ zueinander bewegten Inertialsystemen durch eine Koordinatensystemdrehung um einen imaginären Winkel in einem vierdimensionalen Raum darstellbar ist.
Gegeben sind zwei Inertialsysteme S und S', die sich relativ zueinander mit der Geschwindigkeit v bewegen. Ersetzt man w durch ict und ß durch den imaginären Winkel (iß), dann wird aus der reellen Drehung im euklidischen Raum eine imaginäre Drehung im Minkowski-Raum (x, w=ict). Die imaginäre Einheit in w=ict gewährleistet die pseudoeuklidische Metrik der Minkowski-Raumzeit.
Das ist vorläufig eine willkürliche mathematische Festsetzung ohne physikalische Begründung. Durch diese Festsetzung wird auch der Drehwinkel imaginär. Einstein stand ursprünglich den mathematischen Ideen Minkowskis zur SRT reserviert gegenüber: Er sagte: "Das bringt doch physikalisch nichts Neues!" Später erwies sich Minkowskis imaginärer Ansatz als sehr hilfreich zur späteren mathematischen Herleitung der ART-Gleichungen. Einsteins ursprüngliche Herleitung der ART-Gleichungen war nämlich sehr kompliziert und für einen mathematischen Laien nicht nachvollziehbar. Siehe Skizze 2:
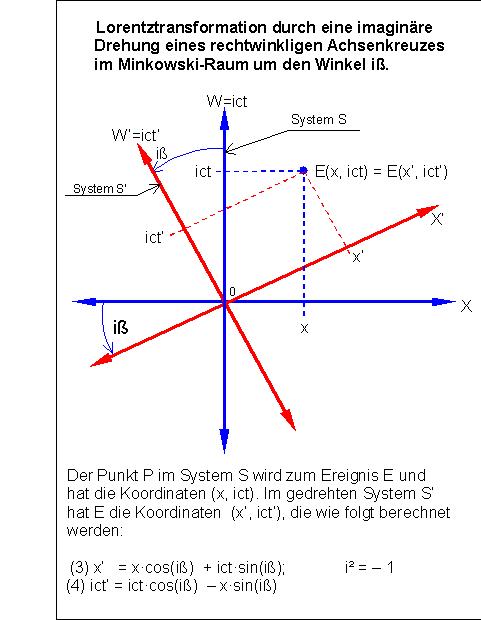
Skizze 2
Der Raumzeit-Abstand O-E bleibt durch die Drehung invariant. Das Ereignis E, das im System S durch den Weltpunkt E(x, ict) dargestellt wird, ist im System S’ der Weltpunkt E(x’, ict’). Bei dem Weltpunkt E handelt sich im System S und im System S’ um das gleiche Ereignis, nur die Koordinaten dieses Ereignisses haben im System S andere Werte als im System S’.
Die Transformationsgleichungen nehmen deshalb folgende Gestalt an:
(3) x' = x•cos(iß) + ict•sin(iß); i2 = – 1
(4) ict' = ict•cos(iß) – x•sin(iß)
Zu jedem Zeitpunkt bewegt sich S' mit der Geschwindigkeit v = x/t in Richtung der positiven x-Achse; daraus folgt:
(5) x = v•t
Betrachtet man im 2. Quadranten des Systems S einen beliebigen Punkt (– x, ict), der auf der auf der Ordinate w=ict' liegt, dann lässt sich für den Winkel (iß) der Tangens bestimmen:
(6) tan(iß) = – x/ict; mit x=v•t ergibt sich:
(7) tan(iß) = – v•t/ict
Für alle t ungleich Null ergibt sich:
(8) tan(iß) = – v/(ic); quadriert ergibt:
(9) tan2(iß) = – v2/c2
Der imaginäre Drehwinkel (iß) repräsentiert somit – über den Tangens dieses Winkels – die Relativgeschwindigkeit zwischen den beiden Inertialsystemen S und S' als Bruchteil der Lichtgeschwindigkeit. Aus einer Formelsammlung entnehme ich die Umformungen (10) und (11):
(10) sin(iß) = tan(iß)/sqrt[1 + tan2(iß)�
(11) cos(iß) = 1/sqrt[1 + tan2(iß)�
Mit der Kurzschreibweise G = 1/sqrt[1 + tan2(iß)� ergibt sich:
(12) sin(iß) = G•tan(iß)
(13) cos(iß) = G; (12) und (13) in (3) eingesetzt ergibt:
(14) x' = x•G + ict•G•tan(iß); mit tan(iß) = – v/(ic) ergibt sich:
(15) x' = x•G + ict•G•[– v/(ic)�
(16) x' = x•G – t•G•v
(17) x' = G(x – v•t); aus (4) und (12) und (13) ergibt sich:
(18) ict' = ict•G – x•G•tan(iß); mit tan(iß) = – v/(ic) ergibt sich:
(19) ict' = ict•G – x•G•[ – v/(ic)�
(20) ict' = G[ ict – x•[ – v/(ic)� ]
(21) ict' = G[ict + x·v/(ic)�; dividiert durch (ic) ergibt:
(22) t' = G(t – x•v/c2)
Wenn man die Beziehung (9) in die Kurzschreibweise
G = 1/sqrt[1 + tan2(iß)� einsetzt, dann ergibt sich:
(23) G = 1/sqrt(1 – v2/c2)
Diese Gleichung in (17) und (22) eingesetzt ergeben die speziellen Lorentz-Transformationen:
x' = (x – v•t) / sqrt(1 – v2/c2)
t' = (t – v•x/c2) / sqrt(1 – v2/c2)
Neue Ergänzungen
13.03.2013, 19:99 Die Lorentz-Transformationen, hergeleitet aus der Drehung eines Koordinatensystems in der Minkowski-Raumzeit {x, y, z, w=ict}.
06.04.2013, 11:34 Relativistische Masse gelöscht.
06.04.2013, 11:34 Energie-Impuls-Beziehung neu eingebracht.
16.04.2013, 14:25 Lichtgeschwindigkeits-Defintion.
21.04.2013, 17:45 Relativität der Bewegung + SRT als Sonderfall der ART.
02.05.2013, 16:40 Begriff der Geschwindigkeit ergänzt.
05.10.2013, 11:34 Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
bitte hier keine Beiträge einstellen!
Warum? Es soll nur der erste Beitrag hier verbleiben, den ich immer auf den neuesten Stand nach Absprache mit Zara.t. bringe. Er soll eine Wissensplattform zur SRT für alle werden, damit jeder darauf zurückgreifen kann, wenn Fragen entstehen. Hier eingehende Beiträge werden weder von mir noch von Zara.t. beantwortet.
Wenn ihr darüber diskutieren möchtet, dann bitte im Thread Basics spezielle Relativitätstheorie! Vielen Dank im Voraus.
M.f.G. Eugen Bauhof
Forenteilnehmer, deren Beiträge bis jetzt hier eingebracht wurden (in alphabetischer Reihenfolge):
Bauhof, Grtgrt, Henry, Okotombrok, Zara.t.
Themen, die demnächst in den SRT-Basics diskutiert werden sollen:
(A) Begriff des Beobachtens.
(B) Maxwellsche Gleichungen.
(C) E = mc2.
(D) Die Lorentz-Transformationen, hergeleitet allein aus dem Relativitätsprinzip.
(E) Transformationen, die das Linienelement ds2 = (c dt)2 - dx2 - dy2 - dz2 invariant lassen.
Inertialsysteme
1. Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig. Alle Inertialsysteme bewegen sich relativ zueinander mit einer Geschwindigkeit v<c.
2. Sich drehende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme.
3. Auch gleichförmig beschleunigte Systeme sind keine Inertialsysteme. Eine gleichförmige Beschleunigung ist keine gleichförmige Bewegung und somit nicht der Ruhe äquivalent.
4. Ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, hat keine Ruhemasse. Deshalb gibt es kein Inertialsystem, in dem Photonen in Ruhe wären.
5. Ein System, in dem sich jeder kräftefreie Körper gleichförmig geradlinig bewegt, wird als Inertialsystem bezeichnet.
6. Das Zusammentreffen von Kräftefreiheit und gleichförmiger Geradlinigkeit sämtlicher Bewegungen gibt es nur in Inertialsystemen.
7. Es kann kein Inertialsystem geben, das sich relativ zu einem zweiten Inertialsystem mit c bewegt. Grund: alle lichtartigen Weltlinien haben die Länge Null.
8. Wenn ein Lichtstrahl im Koordinatenursprung O(0,0,0) startet. dann gilt:
S2 = (ct)2 - x2 - y2 - z2 ; für Licht gilt: x2 + y2 + z2 = (ct)2 ==> S2 = (ct)2 - (ct)2 = 0; S = 0
Wichtig: S ist für alle (also auch für die nicht lichtartigen) Weltlinien invariant unter Lorentztransformationen. Das heißt: die Eigenzeit eines Systems ist eine absolute Größe, sie ist die Zeit, die eine mit diesem System fest verbundene Borduhr anzeigt.
Relativitätsprinzip
1. Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen werden.
2. Alle Inertialsysteme sind gleichberechtigt, wenn es gilt Naturgesetze zu formulieren. Naturgesetze müssen kovariant formuliert werden können.
3. Alle Beobachter, die sich mit gleichförmiger Geschwindigkeit relativ zueinander bewegen, sind gleichermaßen zu der Behauptung berechtigt, sie befinden sich in Ruhe.
Absolute Ruhe
Die Physik kennt keine absolute Ruhe. Die Gesetze der Physik lauten in allen Inertialsystemen gleich und zeichnen keines aus (Relativitätsprinzip). Es gibt nur relative Ruhe, Ruhe in bezug auf ein spezielles Inertialsystem, das momentane Ruhsystem.
Absolutgeschwindigkeit
Mit keinem Experiment kann eine Absolutgeschwindigkeit eines Inertialsystems bestimmt werden; kein Experiment lässt die Unterscheidung von Ruhe und gleichförmiger Bewegung zu. Damit war auch das vor Einstein der als absolut ruhendes Lichtwellen-Trägermedium angesehene "Lichtäther" gegenstandslos, den "Lichtäther" gibt es nicht.
Beobachten
Unter Beobachten versteht man die Feststellung der Koordinaten von Ereignissen in einem Inertialsystem. Wenn man das wirkliche Beobachten meint, muss man die endliche Laufzeit des Lichtsignals vom Gegenstand zum Betrachter berücksichtigen.
Den Begriff des Beobachtens möchte Zara.t. noch diskutieren. Er ist von zentraler Wichtigkeit um das Denken und die Arbeitsweise Einsteins zu verstehen.
Lichtgeschwindigkeit
1. Die Lichtgeschwindigkeit ist eine physikalische Naturkonstante und hat einen exakt definierten Wert.
2. Man kann c=1 setzen. Um hier im Forum Missverständnisse zu vermeiden, wird folgendes vereinbart:
3. Die Existenz einer invarianten Grenzgeschwindigkeit folgt aus dem Relativitätsprinzip. Der Wert dieser Grenzgeschwindigkeit wird von den Maxwellschen Gleichungen festgelegt und durch alle Messungen bisher bestätigt.
4. Aus den Maxwellschen Gleichungen ergibt sich die Ausbreitungsgeschwindigkeit c elektromagnetischer Wellen aus zwei experimentell herausgefundenen Konstanten:
c = 1/sqrt(ε0 • ε0)
ε0 = magnetische Feldkonstante.
ε0 = elektrische Feldkonstante.
Eigenzeit einer Uhr
Die Eigenzeit einer Uhr entspricht immer der Länge ihrer Weltlinie.
Länge der Weltlinie eines bewegten Objekts
Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit... Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Maxwellsche Gleichungen
Die Maxwellschen Gleichungen sagen in einfachen Worten: Die Änderung eines elektrischen Feldes induziert ein magnetisches Feld, die Änderung des magnetischen Feldes induziert ein elektrisches Feld, das sich ändernde elektische Feld induziert ein Magnetfeld, usw....dieser ständige Wechsel breitet sich wellenförmig mit c (im Vakuum) aus. Die Maxwellschen Gleichungen sind früher als die SRT unabhängig von der SRT entstanden. An ihrem Beispiel könnten wir zeigen, was eine kovariante Formulierung ist. So wie Maxwell seine Gleichungen formulierte, waren sie nämlich noch nicht kovariant. Man kann ihnen aber eine kovariante Form verpassen.
Energie-Impuls-Beziehung
Die Energie-Impuls-Beziehung ist eine invariante Größe:
E2 – (pc)2 = (mc2)2 || = constant
E..................Gesamtenergie, sie ist bezugssystemabhängig.
p...................Impuls, er ist bezugssystemabhängig.
mc2:=E0.......Ruheenergie sie ist bezugssystemunabhängig.
Nachdem die Ruheenergie bezugssystemunabhängig ist, ist auch die Masse m invariant.
SRT-Glossar
Äther
Ein Medium, in dem sich Licht und andere elektromagnetische Wellen fortpflanzen sollten. Diese Vorstellung wurde, vor allem nach der Entdeckung der Speziellen Relativitätstheorie, durch eine Feldbeschreibung ersetzt, nach der sich elektromagnetische Wellen auch ohne jedes Medium im leeren Raum fortpflanzen können. Die Vorstellung vom Äther wurde durch die Relativitätstheorie widerlegt.
Beobachter
Idealisierte Person oder Apparatur, oft hypothetischer Natur, die relevante Eigenschaften eines physikalischen Systems misst. Jeder Beobachter, der sich inertial bewegt, darf annehmen, dass er selbst in Ruhe sei. Er beobachtet lediglich, dass alle anderen Beobachter sich relativ zu ihm bewegen oder in Ruhe sind. Mehr kann er nicht beobachten, insbesondere kann er keine Eigenbewegung aus den Bewegungen anderer ableiten. Für ihn sieht es so aus, als würde er ruhen und alle anderen Beobachter bewegen sich.
Beschleuniger
Ein Instrument, das die Geschwindigkeit, und damit die Energie, geladener Teilchen erhöht. Beschleunigt werden können stabile Teilchen wie Elektron, Proton und Ionen.
Beschleunigung
Eine Veränderung der Geschwindigkeit, das heißt des Geschwindigkeitsbetrags und/oder der Bewegungsrichtung eines Objekts.
Bezugssystem
Die räumliche Beschreibung von Vorgängen braucht ein Bezugssystem (Koordinatensystem, Koordinaten) In einem Bezugssystem kann man die Bewegung eines Körpers beschreiben, ebenso aber auch die Bewegung eines anderen Bezugsystems, z. B. eine gradlinig gleichförmige Bewegung eines Bezugssystems in einem anderen, oder auch eine Drehung, eine krummlinige Bewegung oder eine beliebige Beschleunigung. Die Spezielle Relativitätstheorie diskutiert die Frage, wie sich zwei Beschreibungen desselben Vorgangs zueinander verhalten, die zu Bezugssystemen gehören die gegeneinander gleichförmig bewegt sind. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme.
Dilatation
Das Auseinanderziehen, die Verlängerung. Hier gebraucht im Zusammenhang mit Zeitdilatation, d.h. die Verlängerung der Zeiten in einem bewegten System gemäß der Speziellen Relativitätstheorie.
Doppler-Effekt-Verschiebung
Verschiebung der Spektrallinien einer Strahlung durch die Bewegung ihrer Quelle relativ zur Sichtlinie. Annäherung verursacht Blauverschiebung, Entfernung Rotverschiebung.
Eigenzeit
Eigenzeit ist die Zeit, gemessen von einer Uhr, welche die Bewegung eines Beobachters mitmacht. Uhren in relativer Bewegung zu einem Beobachter messen, dass seine und die Eigenzeit verschieden schnell vergehen. Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit. Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Elektrodynamik
Theorie der elektrischen und magnetischen Erscheinungen, zusammengefasst in der einheitlichen Elektrodynamik am Ende des 19. Jahrhunderts durch Maxwell. Dazu gehört vor allem die Theorie der elektromagnetischen Wellen, wie z. b. Radiowellen, Licht oder Gammastrahlen.
Elektromagnetische Welle
Eine wellenartige Störung in einem elektromagnetischen Feld. Alle diese Wellen breiten sich mit Lichtgeschwindigkeit aus. Sichtbares Licht, Röntgenstrahlen, Mikrowellen und Infrarotstrahlung sind Beispiele dafür.
Energie
Physikalische Grundgroße, für die ein strenger Erhaltungssatz gilt. Sie kann verschiedene Formen annehmen, z. B. die potentielle Energie eines im Schwerefeld hochgehobenen Gewichts, die kinetische Energie eines bewegten Körpers, die Wärmeenergie, in die schließlich jede Energie anderer Formen übergeht, oder die als Masse vorhandene Energie gemäß der Speziellen Relativitätstheorie. ("Trägheit der Energie")
Ereignis
Ein Weltpunkt in der Raumzeit. Beschrieben durch vier Koordinaten: {x, y, z. t}.
Frequenz
Die Zahl vollständiger Wellenzyklen, die eine Welle pro Zeiteinheit durchläuft.
Grobes Missverständnis der SRT.
Etliche Kritiker der SRT in den letzten 100 Jahren glaubten, die relativistische Zeitdilatation sei ein rein "perspektivischer" Beobachtungs-Effekt und allein durch die Lichtlaufzeiten zum Beobachter zu erklären. Ein ganz grobes Missverständnis der SRT.
Geschwindigkeit
Der Geschwindigkeitsbetrag und die Bewegungsrichtung eines Objekts, zu einer Größe zusammengefasst. Die Geschwindigkeit ist differentiell definiert als Ortsänderung pro Zeiteinheit.: v = dx/dt. Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle, deren Radius sich mit 299 752 458 m/sec vergrößert. Ihr Durchmesser aber vergrößert sich doppelt so schnell. Das ist kein Widerspruch zur SRT, da die Rate, mit der sich ein Abstand vergrößert, nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann. Diese Vergrößerung des Durchmessers kann nicht mit der Einsteinschen Geschwindigkeitsadditions-Formel berechnet werden, weil es sich bei der Verdoppelung des Durchmessers nicht um eine Geschwindigkeit im Sinne der SRT handelt.
Gleichzeitigkeit
In der klassischen Mechanik ist die Gleichzeitigkeit von Ereignissen unabhängig von jedem Bewegungszustand und von der Entfernung definiert. In der speziellen Relativitätstheorie hängt die Definition der Gleichzeitigkeit von der Relativ-Geschwindigkeit und von der Entfernung ab (Einsteins Relativität der Gleichzeitigkeit).
Gleichzeitigkeits-Definition von Einstein
"Die für A und B gemeinsame Zeit kann so definiert werden, indem man durch Definition festsetzt, dass die Zeit, welche das Licht braucht, um von A nach B zu gelangen, gleich ist der Zeit, welche es braucht, um von B nach A zu gelangen."
Für entfernte Punkte kann man zu einer Gleichzeitigkeits-Definition also überhaupt nur gelangen auf dem Wege eines konstruktiven Postulats, in dem gefordert wird, dass die Ausbreitung des Lichtes, gemessen in der noch zu definierenden gemeinsamen Zeit, ein Vorgang mit konstanter Geschwindigkeit ist. Dieses Postulat ist entscheidend an der Konstruktion des Begriffs der gemeinsamen Zeit beteiligt.
Ideale Uhren.
Zur Herleitung der Theorien (der SRT und der ART) legt man sogenannte "ideale" Uhren zugrunde. So eine ideale Uhr wird realisiert durch Atomuhren. Reale Experimente, welche die SRT belegen, werden mit den Taktraten von Atomuhren durchgeführt
Inertialsystem.
Ein Inertialsystem ist ein Bezugssystem, in dem sich kräftefreie Körper geradlinig gleichförmig bewegen. Das bedeutet, dass es sich bei einem Inertialsystem um ein nicht rotierendes und nicht beschleunigtes Bezugssystem handelt. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme. Somit bewegen sich Körper, auf die keine Kräfte wirken, in allen Inertialsystemen auf Geraden. Eine gleichförmige Rotationsbewegung wäre demzufolge nichtinertial. Jeder nichtrotierende Beobachter, der sich gleichförmig und unbeschleunigt bewegt, befindet sich in einem Inertialsystem. Auf ihn wirken keine Kräfte.
Es gibt kein ausgezeichnetes Inertialsystem, von dem man behaupten könnte, es sei absolut ruhend. Es gibt keinen Punkt im Universum, von dem man sagen könnte, das sei allein der "absolut ruhende Pol", auf dem man jede andere Bewegung beziehen könnte. Insbesondere gibt es auch keinen "absoluten Raum", auf dem man alle Bewegungen beziehen könnte. Sowohl in der klassischen Mechanik wie in der Speziellen Relativitätstheorie sind alle Inertialsysteme für die Beschreibung gleichberechtigt.
Isotropie
Unabhängigkeit von Richtung oder Winkel. In einem isotropen Universum sind sämtliche messbaren Größen in allen Richtungen gleich.
Invarianz
Die Unveränderlichkeit bestimmter Größen oder Beziehungen, auch wenn andere Charakteristika transformiert werden. Invarianz-Überlegungen der Physik beziehen sich gewöhnlich auf die Invarianz von Größen gegenüber Transformationsgruppen.
Invarianz der Lichtgeschwindigkeit.
Unter der Invarianz der der Lichtgeschwindigkeit versteht man z.B. folgendes: Für das Licht wird immer die gleiche Geschwindigkeit gemessen, unabhägig davon, ob sich die Lichtquelle auf uns zu- oder von uns fortbewegt. Das sehen alle Beobachter so, gleichgültig, ob sie auf der Lichtquelle sitzen oder ob sie sich außerhalb befinden und die Lichtquelle als bewegt wahrnehmen. Daraus folgt: Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich groß.
Kinematik der Relativitätstheorie
Die Grundlagen der Relativitätstheorie können durch geometrische Intuition erschlossen werden. Die Kinematik der Relativitätstheorie kann daher als die Geometrie der Raumzeit-Union angesehen werden.
Kinetische Energie
ist die mit der Bewegung verknüpfte Energie; sie ist gleich der Arbeit, die geleistet werden muss, um einen Körper der Masse m aus dem Ruhezustand in einen Bewegungszustand mit der Geschwindigkeit v zu bringen. Sie beträgt in der klassischen Mechanik 1/2•m•v2.
Konstanz der Lichtgeschwindigkeit
Darunter versteht man die Unabhängigkeit von der Ausbreitungsrichtung und die Unveränderlichkeit ihrer Größe bei Zusammensetzung.
Unabhängigkeit von der Ausbreitungsrichtung heißt zum Beispiel: Wenn ein Lichtstrahl senkrecht auf eine Spiegelfläche mit der Geschwindigkeit v=c trifft, dann hat auch der reflektierte Strahl die Geschwindigkeit v=c. Strahlen, die nicht senkrecht auftreffen, werden ebenfalls mit der Geschwindigkeit v=c reflektiert.
Kovariant
Die Beschreibung eines physikalischen Systems ist kovariant, wenn bei einer Transformation des Systems die transformierte Beschreibung des transformierten Systems dieselben Ergebnisse liefert wie die ursprüngliche Beschreibung des ursprünglichen Systems.
Lichtlaufzeiten.
Mit den Lichtlaufzeiten zum Beobachter sind die relativistischen Effekte nicht erklärbar. Das schließt nicht aus, dass man zum besseren Verstehen Gedankenexperimente macht, in denen die Lichtlaufzeiten mit einbezogen werden.
Lichtuhr
Eine hypothetische Uhr, welche die verstrichene Zeit misst, indem sie zählt, wie viele vollständige Rundreisen ein einzelnes Photon zwischen zwei Spiegeln zurücklegt.
Lorentz-Kontraktion
Besonderheit, die sich aus der speziellen Relativitätstheorie ergibt. Ein bewegtes Objekt erscheint einem ruhenden Beobachter, der dessen Länge misst, in Richtung der Bewegung verkürzt.
Minkowski-Raumzeit
Minkowski erkannte, dass die Kinematik der SRT graphisch darstellbar wird, wenn man neben den altbekannten kartesischen Koordinatenachsen x, y, z noch die vierte Achse ict einführt und sich bei der Veranschaulichung relativistischer Raum-Zeit-Verhältnisse auf jeweils zwei Achsen, typischerweise die Achsen x und ict, beschränkt. Für die Abstände zwischen Weltpunkten, die jetzt Raum- und Zeitkoordinaten hatten, galt die alte euklidische Regel quadrierter Koordinaten-Differenzen, allerdings mit einem durch i2 = –1 veränderten Vorzeichen des zeitlichen Anteils:
ds2 = dx2 + dy2 + dz2 + d(ict)2
Die Lorentztransformationen konnten dann als Drehung in dieser vierdimensionalen Raumzeit verstanden werden, bei der diese Größe ds2 invariant blieb ebenso wie bei Drehung im dreidimensionalen Raum der dreidimensionale Abstand zweier Körper unverändert bleibt. Effekte wie die Lorentzkontraktion und die Zeitdilatation konnten nun als durch Projektion von Längen- und Zeitanteil von eigentlich längen- und zeitbehafteten Größen auf zueinander um den Winkel ß = arctan(v/c) gedrehte Koordinatenachsen anschaulich interpretiert werden.
Mittelpunkt im Universum.
Im Universum ist kein Ort feststellbar, der als Mittelpunkt im Universum bezeichnet werden könnte.
Newtonsche Bewegungsgesetze
Gesetze, welche die Bewegung von Körpern unter Kräfteeinfluss beschreiben, wobei sie voraussetzen, dass Raum und Zeit absolut und unwandelbar sind. Diese Gesetze galten unverändert, bis Einstein die spezielle Relativitätstheorie entdeckt hatte, die zeigt, dass die Newtonsche Theorie nur eine Näherung für den Grenzfall kleinerer Geschwindigkeiten ist.
Photon
Kleinstes Paket des elektromagnetischen Felds. Botenteilchen der elektromagnetischen Kraft. Kleinstes Lichtpaket.
Pseudoeuklidische Geometrie
Während in einem euklidischen Raum das Quadrat des Abstandes zweier verschiedener Punkte P1 und P2 stets größer als Null ist, kann es in der Minkowski-Welt auch kleiner oder gleich Null sein. Die Raumzeit-Union der Relativitätstheorie besitzt also keine euklidische Maßbestimmung. Vielmehr ist die Maßbestimmung die vierdimensionale Verallgemeinerung der pseudo-euklidischen Geometrie. Dies ist der mathematische Ausdruck dafür, dass die Zeitkoordinate eine andere Qualität als die 3 Raumkoordinaten besitzt.
Raum und Zeit als untrennbare Einheit.
Man kann die SRT nicht auf der Grundlage der klassischen Betrachtung mit Trennung von Raum und Zeit verstehen. Man kann die SRT erst dann verstehen, wenn man Raum und Zeit als untrennbare Einheit ansieht.
Raumzeit
Die drei physikalischen Dimensionen des Raums werden mit der Zeit, die als vierte Dimension aufgefasst wird, verknüpft und ergeben so das Raum-Zeit-Kontinuum, das den grundlegenden Rahmen in der Relativitätstheorie darstellt.
Relativgeschwindigkeit.
Jede Geschwindigkeit (eines Körpers oder eines Inertialsystems) ist immer nur eine Relativgeschwindigkeit.
Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in Bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
Relativität der Gleichzeitigkeit.
Das ist die erste Konsequenz der Konstanz der Lichtgeschwindigkeit. Einstein argumentierte etwa wie folgt: Auch die Zeit ist relativ. Es gibt keine absolute Zeit, die für alle Inertialsysteme gültig ist. In jedem Inertialsystem läuft die Zeit anders ab, abhängig davon, wie schnell sich die Inertialsysteme relativ zueinander bewegen. Und das ist ein totaler Umsturz unseres Weltbildes, weil seit Newton die Zeit "überall gleich verfließt". Und genau das tut sie nicht.
Was für einen Beobachter gleichzeitig ist, ist für einen anderen bewegten Beobachter nicht gleichzeitig. Ob zwei räumlich getrennt liegende Ereignisse gleichzeitig sind oder nicht, kann nicht dadurch entschieden werden, dass man mit Hilfe einer Messung die Gleichzeitigkeit zweier Ereignisse feststellen könnte. Der Gleichzeitigkeits-Begriff getrennt liegender Ereignisse erlangt erst durch eine Definition seine Bestimmtheit. Gleichzeitigkeit ist objektiv unbestimmt.
Relativitätsprinzip
Zentraler Begriff der Relativitätstheorie, nach der die physikalischen Gesetze für alle Beobachter, die mit konstanter Geschwindigkeit relativ zueinander bewegt sind, die gleiche Form haben; daher ist jeder dieser Beobachter gleichermaßen zu der Behauptung berechtigt, er befinde sich in Ruhe. Dieses Prinzip wird in der allgemeinen Relativitätstheorie zum Äquivalenzprinzip erweitert. Bereits in der Newtonschen Mechanik waren alle Inertialsysteme gleichberechtigt. Die Newtonschen Axiome der Mechanik zeichnen kein Inertialsystem gegenüber dem anderen aus. Der Übergang von einem Inertialsystem in ein anderes Inertialsystem wird in der Newtonschen Mechanik durch eine Galilei-Transformation vollzogen.
Relativistischer Dopplereffekt
Der relativistische Dopplereffekt hängt nur von der Relativgeschwindigkeit von Sender und Empfänger ab.
Ruheenergie
ist die aus der Beziehung E0 = mc2 berechnete Energie , wobei m die Masse des Teilchens und c die Lichtgeschwindigkeit ist. Die Ruhenergie wird nur dann vollständig freigesetzt, wenn ein Teilchen mit seinem Antiteilchen zerstrahlt.
Ruhesystem.
Man kann sich als Beobachter in jedes beliebige Inertialsystem gedanklich hineinsetzen kann, um dieses Inertialsystem dann zum Ruhesystem zu erklären.
Spezielle Relativitätstheorie
Einsteins Gesetze von Raum und Zeit in Abwesenheit von Gravitation.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
Teilchenbeschleuniger
Anlage, die Teilchen fast auf Lichtgeschwindigkeit beschleunigt und sie dann mit anderen Teilchen zusammenstoßen lässt, um ihren materiellen Aufbau zu ermitteln.
Vektorraum
In der Mathematik eine Gesamtheit von Vektoren, d.h. Objekten, die sich addieren und mit Zahlen multiplizieren lassen. Vektorräume unterscheiden sich nach der Art dieser Zahlen (z. b. reelle oder komplexe Zahlen) und nach ihrer Dimensionszahl. Zum Beispiel bilden die möglichen Geschwindigkeiten im Raum einen dreidimensionalen reellen Vektorraum.
Vierdimensionaler Abstand zwischen zwei Ereignissen.
Für alle inertialen Beobachter ist der vierdimensionale Abstand zwischen zwei Ereignissen in der Raumzeit verbindlich. Alle messen den gleichen Wert. Man sagt, dieser Abstand ist das "Raumzeit-Intervall" und dieses ist invariant für alle Beobachter. Wenn man die zwei Raumdimensionen y und z weglässt und nur eine Raumdimension x und die Zeitdimension t betrachtet, dann ergibt sich das Raumzeit-Intervall s2 zwischen zwei Ereignissen für zwei verschiedene Systeme wie folgt:
Wellenlänge
Elektromagnetische Strahlung wird durch ihre Wellenlänge oder ihre Frequenz charakterisiert, deren Produkt gleich der Lichtgeschwindigkeit ist. Die Wellenlänge ist die Entfernung zwischen aufeinanderfolgenden Wellenfronten, und die Frequenz ist die Zahl der Wellenfronten, die an einen gegebenen Punkt in einer Sekunde vorbeilaufen. Im sichtbaren Bereich hat das Licht eine Wellenlänge von 400 bis 700 Nanometer und eine Frequenz von 7 x 1014 bis 4 X 1014 Hertz.
Weltlinie
Eine Abfolge von Weltpunkten.
Weltpunkt
Ein Ort in der Raumzeit. Er ist bestimmt durch vier Koordinaten: {x, y, z, t}
Zwillingsparadoxon.
Gegen Einsteins Zwillingsexperiment wird meist mit der Symmetrie der Zeitdilatation argumentiert:
Wenn Zwilling B einerseits die Uhr von Zwilling A langsamer gehen sieht, dann muss umgekehrt doch Zwilling A auch die Uhr von B langsamer gehen sehen. Das ist zwar richtig, gilt aber nur, solange sich Zwilling A und B jeweils in einem Inertialsystem bewegen. Doch Zwilling B muss umkehren, um zu A zurückkehren zu können, d. h., er beschleunigt und befindet sich daher nicht in einem Inertialsystem, im Gegensatz zu B.
Diese Antwort wiederum hat dazu geführt, dass oftmals die Beschleunigungsphasen von B für die Verjüngung verantwortlich gemacht werden. Aber auch das ist nicht richtig, wie sich leicht zeigen lässt, indem man aus dem Zwillingsparadoxon ein Drillingsparadoxon macht. In der nachstehenden Skizze sind die Weltlinien der Drillinge A, B und C dargestellt, wobei C identische Beschleunigungsphasen (gekrümmte Kurvenstücke, durchgezogen gezeichnet) durchläuft, allerdings ist seine Reise kürzer.

Nach Zusammenkunft aller drei ist A älter als C und C älter als B. Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden. Es ist die physikalische Geometrie der relativistischen Raumzeit: Der Weg von B ist kürzer als der von C, und dieser wiederum ist kürzer als der Weg von A.
Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
1. Die Symmetrie der Zeitdilatation wird gebrochen, sobald der reisende Zwilling umkehrt.
2. Die Umkehr ist gleichbedeutend mit einem Inertialsystemwechsel.
3. Der Inertialsystemwechsel bei der Umkehr lässt die auf seiner Reise erarbeitete Zeitdilatation des reisenden Zwillings manifest werden.
4. Die verflossene Eigenzeit, die der jeweilige Zwilling auf seiner Uhr abliest, entspricht der jeweiligen Länge der Weltlinie im Minkowski-Raum.
5. Die Beschleunigungsphasen des reisenden Zwillings sind nicht die Ursache der Zeitdilatation. Man kann die Beschleunigungsphasen durch ein Differenzexperiment zum Verschwinden bringen. Die Zeitdilatation tritt dann trotzdem auf. Die Zeitdilatation ist im wesentlichen abhängig von der Reisedauer und der Reisegeschwindigkeit des reisenden Zwillings.
6. Manche meinen, dass nur die ART das scheinbare Paradoxon auflösen könnte, weil Beschleunigungen im Spiel sind. Mal ganz abgesehen davon, dass man mit der SRT auch Beschleunigungen beschreiben kann, ist die ART zu Auflösung des Zwillingsparadoxons nicht notwendig. Es kann allein mit Mitteln der SRT gelöst werden. Die ART wird nur dann benötigt, wenn die Gravitation ins Spiel kommt.
Herleitung der Lorentz-Transformationen mit Hilfe einer Koordinatensystemdrehung im Minkowski-Raum.
Zunächst wird die gewöhnliche Koordinatentransformation im euklidischen Raum in Skizze 1 dargestellt, so wie sie in jeder Formelsammlung zu finden ist:

Der Mathematiker Hermann Minkowski Minkowski ging von der Invarianz des Linienelementes aus und suchte allgemeine Transformationsgleichungen, die dies gewährleisten. Er hat dabei herausgefunden, dass allgemein jede Transformation zwischen relativ zueinander bewegten Inertialsystemen durch eine Koordinatensystemdrehung um einen imaginären Winkel in einem vierdimensionalen Raum darstellbar ist.
Gegeben sind zwei Inertialsysteme S und S', die sich relativ zueinander mit der Geschwindigkeit v bewegen. Ersetzt man w durch ict und ß durch den imaginären Winkel (iß), dann wird aus der reellen Drehung im euklidischen Raum eine imaginäre Drehung im Minkowski-Raum (x, w=ict). Die imaginäre Einheit in w=ict gewährleistet die pseudoeuklidische Metrik der Minkowski-Raumzeit.
Das ist vorläufig eine willkürliche mathematische Festsetzung ohne physikalische Begründung. Durch diese Festsetzung wird auch der Drehwinkel imaginär. Einstein stand ursprünglich den mathematischen Ideen Minkowskis zur SRT reserviert gegenüber: Er sagte: "Das bringt doch physikalisch nichts Neues!" Später erwies sich Minkowskis imaginärer Ansatz als sehr hilfreich zur späteren mathematischen Herleitung der ART-Gleichungen. Einsteins ursprüngliche Herleitung der ART-Gleichungen war nämlich sehr kompliziert und für einen mathematischen Laien nicht nachvollziehbar. Siehe Skizze 2:

Der Raumzeit-Abstand O-E bleibt durch die Drehung invariant. Das Ereignis E, das im System S durch den Weltpunkt E(x, ict) dargestellt wird, ist im System S’ der Weltpunkt E(x’, ict’). Bei dem Weltpunkt E handelt sich im System S und im System S’ um das gleiche Ereignis, nur die Koordinaten dieses Ereignisses haben im System S andere Werte als im System S’.
Die Transformationsgleichungen nehmen deshalb folgende Gestalt an:
(3) x' = x•cos(iß) + ict•sin(iß); i2 = – 1
(4) ict' = ict•cos(iß) – x•sin(iß)
Zu jedem Zeitpunkt bewegt sich S' mit der Geschwindigkeit v = x/t in Richtung der positiven x-Achse; daraus folgt:
(5) x = v•t
Betrachtet man im 2. Quadranten des Systems S einen beliebigen Punkt (– x, ict), der auf der auf der Ordinate w=ict' liegt, dann lässt sich für den Winkel (iß) der Tangens bestimmen:
(6) tan(iß) = – x/ict; mit x=v•t ergibt sich:
(7) tan(iß) = – v•t/ict
Für alle t ungleich Null ergibt sich:
(8) tan(iß) = – v/(ic); quadriert ergibt:
(9) tan2(iß) = – v2/c2
Der imaginäre Drehwinkel (iß) repräsentiert somit – über den Tangens dieses Winkels – die Relativgeschwindigkeit zwischen den beiden Inertialsystemen S und S' als Bruchteil der Lichtgeschwindigkeit. Aus einer Formelsammlung entnehme ich die Umformungen (10) und (11):
(10) sin(iß) = tan(iß)/sqrt[1 + tan2(iß)�
(11) cos(iß) = 1/sqrt[1 + tan2(iß)�
Mit der Kurzschreibweise G = 1/sqrt[1 + tan2(iß)� ergibt sich:
(12) sin(iß) = G•tan(iß)
(13) cos(iß) = G; (12) und (13) in (3) eingesetzt ergibt:
(14) x' = x•G + ict•G•tan(iß); mit tan(iß) = – v/(ic) ergibt sich:
(15) x' = x•G + ict•G•[– v/(ic)�
(16) x' = x•G – t•G•v
(17) x' = G(x – v•t); aus (4) und (12) und (13) ergibt sich:
(18) ict' = ict•G – x•G•tan(iß); mit tan(iß) = – v/(ic) ergibt sich:
(19) ict' = ict•G – x•G•[ – v/(ic)�
(20) ict' = G[ ict – x•[ – v/(ic)� ]
(21) ict' = G[ict + x·v/(ic)�; dividiert durch (ic) ergibt:
(22) t' = G(t – x•v/c2)
Wenn man die Beziehung (9) in die Kurzschreibweise
G = 1/sqrt[1 + tan2(iß)� einsetzt, dann ergibt sich:
(23) G = 1/sqrt(1 – v2/c2)
Diese Gleichung in (17) und (22) eingesetzt ergeben die speziellen Lorentz-Transformationen:
x' = (x – v•t) / sqrt(1 – v2/c2)
t' = (t – v•x/c2) / sqrt(1 – v2/c2)
13.03.2013, 19:99 Die Lorentz-Transformationen, hergeleitet aus der Drehung eines Koordinatensystems in der Minkowski-Raumzeit {x, y, z, w=ict}.
06.04.2013, 11:34 Relativistische Masse gelöscht.
06.04.2013, 11:34 Energie-Impuls-Beziehung neu eingebracht.
16.04.2013, 14:25 Lichtgeschwindigkeits-Defintion.
21.04.2013, 17:45 Relativität der Bewegung + SRT als Sonderfall der ART.
02.05.2013, 16:40 Begriff der Geschwindigkeit ergänzt.
05.10.2013, 11:34 Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
Beitrag zuletzt bearbeitet von Bauhof am 05.10.2013 um 11:35 Uhr.
Beitrag 1985-355
-
Hallo Eugen,
in Arbeitsplattform SRT schreibst du:
Diese Argumentation finde ich nicht schlüssig. Meiner Meinung nach sollte da stehen:
Gruß, grtgrt
Hallo Eugen,
in Arbeitsplattform SRT schreibst du:
Zitat von Bauhof:
4. Ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, hat keine Ruhemasse. Deshalb gibt es kein Inertialsystem, in dem Photonen in Ruhe wären.
Diese Argumentation finde ich nicht schlüssig. Meiner Meinung nach sollte da stehen:
Zitat von Grtgrt:
4. Für jedes Objekt X, welches sich in einem Inertialsystem gleichförmig mit einer Geschwindigkeit v < c bewegt, gibt es ein Inertialsystem, in dem X ruht.
Note: Da sich ein Photon aus Sicht anderer Objekte in j e d e m Bezugssystem mit Lichtgeschwindigkeit bewegt, gibt es kein Bezugssystem – und insbesondere kein Inertialsystem –, in dem ein Photon ruht.
Gruß, grtgrt
Beitrag 1985-229
Erste Frage
Frage an Dich, Eugen (bzw. an alle):
Ist die SRT auch noch anwendbar auf Bezugssysteme, die sich geradlinig und gleichförmig mit Lichtgeschwindigkeit zueinander bewegen?
Mir ist zwar klar, dass die Formeln der Lorentz-Transformation dann undefiniert werden. Aber könnte man sie nicht als Grenzwert v gegen c an der Stelle v = c dennoch irgendwie sinnvoll anwenden?
Gruß,
grtgrt
Siehe dazu auch die mögliche, in Beitrag 2035-1 skizzierte Anwendung.
Bauhof aus 1991-1:
Inertialsysteme
Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig.
Alle Inertialsysteme bewegen sich relativ zueinander mit einer Geschwindigkeit v<c.
Frage an Dich, Eugen (bzw. an alle):
Ist die SRT auch noch anwendbar auf Bezugssysteme, die sich geradlinig und gleichförmig mit Lichtgeschwindigkeit zueinander bewegen?
Mir ist zwar klar, dass die Formeln der Lorentz-Transformation dann undefiniert werden. Aber könnte man sie nicht als Grenzwert v gegen c an der Stelle v = c dennoch irgendwie sinnvoll anwenden?
Gruß,
grtgrt
Siehe dazu auch die mögliche, in Beitrag 2035-1 skizzierte Anwendung.
Beitrag 1985-230
-
Definitiv nein.
Es ist kein Inertialsystem denkbar, in dem das Licht ruht.
mfg okotombrok�
Grtgrt aus 1985-229:Ist die SRT auch noch anwendbar auf Bezugssysteme, die sich geradlinig und gleichförmig mit Lichtgeschwindigkeit zueinander bewegen?
Definitiv nein.
Es ist kein Inertialsystem denkbar, in dem das Licht ruht.
mfg okotombrok�
Beitrag 1985-15
Inertialsystem und das Relativitätsprinzip der SRT
Ich schlage vor, das so zu formulieren:
Gruß, grtgrt
Bauhof aus 1985-8:
Relativitätsprinzip
Die Unabhängigkeit der Erscheinungen vom Inertialsystem bezeichnet man als das Relativitätsprinzip.
Bessere Formulierng von Zara.t.:
Das Relativitätsprinzip sagt, dass alle Inertialsysteme gleichberechtigt sind, wenn es gilt Naturgesetze zu formulieren. Naturgesetze müssen kovariant formuliert werden können.
Ich schlage vor, das so zu formulieren:
- Relativitätsprinzip : Man versteht darunter die Tatsache, dass die Wahrnehmungen des Beobachters i.A. abhängig von seinem Bezugssystem sind.
- Inertialsystem : Ein Koordinatensystem, in dem sich jeder Körper, auf den keine Kraft wirkt, mit konstanter Geschwindigkeit geradlinig bewegt. Konsequenz daraus: Jedes Koordinatensystem, welches sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegt, ist ebenfalls ein Inertialsystem.
- Naturgesetz : Ein Sachverhalt, der sich dem Beobachter in jedem Inertialsystem gleich darstellt.
Gruß, grtgrt
Beitrag 1985-20
-
Hi Zara,
deine Formulierung sagt einerseits Richtiges, hat aber andererseits den Schönheitsfehler, einem Unkundigen rein gar nichts zu sagen (da sie auf Fachbegriffen aufsetzt, die sie selbst nicht definiert: "Inertialsystem" und "kovariant").
Einsteins eigene Formulierung scheint mir da viel hilfreicher zu sein. Er formulierte das Relativitätsprinzip der SRT so:
Mein Formulierungsvorschlag aus 1985-15 war zudem gedacht, eine missverständliche Formulierung zu beseitigen, die Eugen auch in seiner korrigierten Version von 1985-8 noch stehen hat. Er sagt dort
meint damit aber:
Die Unabhängigkeit der Formulierbarkeit von Naturgesetzen vom Inertialsystem bezeichnet man als das Relativitätsprinzip.
Denn dass die Erscheinungen eben NICHT vom Bezugssystem des Beobachters unabhängig sind (auch wenn es ein Inertialsystem ist), zeigt die Tatsache, dass nach der SRT zwei zueinander gleichförmig bewegte Beobachter die Uhr des jeweils anderen langsamer gehen sehen.
Gruß, grtgrt
Zara.t. aus 1985-19:Relativitätsprinzip: alle Inertialsysteme sind gleichberechtigt, wenn es gilt Naturgesetze zu formulieren.
woraus folgt: Naturgesetze müssen kovariant formuliert werden.
Das Relativitätsprinzip ist der Kern der SRT.
Hi Zara,
deine Formulierung sagt einerseits Richtiges, hat aber andererseits den Schönheitsfehler, einem Unkundigen rein gar nichts zu sagen (da sie auf Fachbegriffen aufsetzt, die sie selbst nicht definiert: "Inertialsystem" und "kovariant").
Einsteins eigene Formulierung scheint mir da viel hilfreicher zu sein. Er formulierte das Relativitätsprinzip der SRT so:
Zitat von Albert Einstein in: Annalen der Physik. 322 Nr 10, 1905, S. 891-921 :
Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon,
auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen werden.
Mein Formulierungsvorschlag aus 1985-15 war zudem gedacht, eine missverständliche Formulierung zu beseitigen, die Eugen auch in seiner korrigierten Version von 1985-8 noch stehen hat. Er sagt dort
Zitat von Bauhof:Die Unabhängigkeit der Erscheinungen vom Inertialsystem bezeichnet man als das Relativitätsprinzip.
meint damit aber:
Denn dass die Erscheinungen eben NICHT vom Bezugssystem des Beobachters unabhängig sind (auch wenn es ein Inertialsystem ist), zeigt die Tatsache, dass nach der SRT zwei zueinander gleichförmig bewegte Beobachter die Uhr des jeweils anderen langsamer gehen sehen.
Gruß, grtgrt
Beitrag 1985-214
-
Die erste kursiv gedruckte Aussage scheint auch mir sehr wichtig (da ich selbst lange Zeit nicht sicher war, ob andere das wirklich so sagen wollten).
Statt von "Invarianz der Lichtgeschwindigkeit" sollte man deutlicher von der "Nicht-Relativität der Lichtgeschwindigkeit" sprechen.
Okotombrok aus 1985-213:
Vielleicht kann man folgende Formulierung noch mit einbringen:
"Für das Licht wird immer die gleiche Geschwindigkeit gemessen, unabhägig davon, ob sich die Lichtquelle auf uns zu- oder von uns fortbewegt."
Vielleicht sollte man in diesem Zusammenhang besser von der "Invarianz der Lichtgeschwindigkeit" sprechen.
Die erste kursiv gedruckte Aussage scheint auch mir sehr wichtig (da ich selbst lange Zeit nicht sicher war, ob andere das wirklich so sagen wollten).
Statt von "Invarianz der Lichtgeschwindigkeit" sollte man deutlicher von der "Nicht-Relativität der Lichtgeschwindigkeit" sprechen.
Beitrag 2000-20
Gebhard Greiter's Deutung scheinbarer Überlichtgeschwindigkeit
Anzunehmen, dass im Quantentunnel die SRT versagt, ist NICHT notwendig
In Tunneling Confronts Special Relativity schreibt Günter Nimtz:
Was Nimtz da schreibt, ergab sich als seine Deutung der Ergebnisse von Experimenten, die er zusammen mit Alfons Stahlhofen durchgeführt hatte.
Die beiden Physiker betonen, dass die SRT nicht im Tunnel gilt, der einen "Raum ohne Zeit" darstelle. Denn die gemessene Tunnelzeit entsteht an der Barrierenfront, während in der Barriere, im "Tunnel" also, keine Zeit verloren geht – Raum ohne Zeit. Einer Vermutung von Richard Feynman folgend lasse der Tunneleffekt sich mit virtuellen Photonen erklären, die sich am Ende der Tunnelbarriere wieder in reelle Photonen zurückverwandeln.
Wie mir auffällt, ist diese Deutung aber nicht zwingend.
Die Ergebnisse der Experimente von Nimtz und Stahlhofen ebenso wie die noch genaueren einer anderen Forschergruppe können auch so gedeutet werden, dass die Wahrscheinlichkeit, das Quant im Tunnel — genauer noch: in der Barriere — anzutreffen Null ist (im Widerspruch zu dem, was die Wellenfunktion des Quants zu sagen scheint; sie genau zu errechnen — und auch noch in relativistischer Fassung — ist bisher wohl ohnehin noch niemand gelungen (!)).
Diese meine Deutung scheint mir der von Nimtz und Stahlhofen vorzuziehen, da sie die SRT unangetastet lässt.
Gebhard Greiter (grtgrt), siehe auch Blog
In Tunneling Confronts Special Relativity schreibt Günter Nimtz:
Zitat:
Experiments with evanescent modes and tunneling particles have shown that (i) their signal velocity may be faster than light, (ii) they are described by virtual particles, (iii) they are nonlocal and act at a distance, (iv) experimental tunneling data of phonons, photons, and electrons display a universal scattering time at the tunneling barrier front, and (v) the properties of evanescent, i.e. tunneling modes are not compatible with the special theory of relativity.
Was Nimtz da schreibt, ergab sich als seine Deutung der Ergebnisse von Experimenten, die er zusammen mit Alfons Stahlhofen durchgeführt hatte.
Die beiden Physiker betonen, dass die SRT nicht im Tunnel gilt, der einen "Raum ohne Zeit" darstelle. Denn die gemessene Tunnelzeit entsteht an der Barrierenfront, während in der Barriere, im "Tunnel" also, keine Zeit verloren geht – Raum ohne Zeit. Einer Vermutung von Richard Feynman folgend lasse der Tunneleffekt sich mit virtuellen Photonen erklären, die sich am Ende der Tunnelbarriere wieder in reelle Photonen zurückverwandeln.
Wie mir auffällt, ist diese Deutung aber nicht zwingend.
Die Ergebnisse der Experimente von Nimtz und Stahlhofen ebenso wie die noch genaueren einer anderen Forschergruppe können auch so gedeutet werden, dass die Wahrscheinlichkeit, das Quant im Tunnel — genauer noch: in der Barriere — anzutreffen Null ist (im Widerspruch zu dem, was die Wellenfunktion des Quants zu sagen scheint; sie genau zu errechnen — und auch noch in relativistischer Fassung — ist bisher wohl ohnehin noch niemand gelungen (!)).
Diese meine Deutung scheint mir der von Nimtz und Stahlhofen vorzuziehen, da sie die SRT unangetastet lässt.
Gebhard Greiter (grtgrt), siehe auch Blog
Beitrag 2005-16
Für Dinge, die sich mit Lichtgeschwindigkeit bewegen, steht die Zeit still
Das ist falsch, denn;
Natürlich zeigt diese Argumentation ganz allgemein:
Für Dinge, die sich mit Lichtgeschwindigkeit bewegen, steht die Zeit still.
Gruß, grtgrt
Gerhard245 aus 2005-14:
Wenn Du Lichtgeschwindigkeit erreichen würdest, würde die Zeit lediglich am langsamsten vergehen, aber sie vergeht. Der Zug und Du, ihr würdet beide bei Lichtgeschwindigkeit älter werden, wenn auch viel langsamer.
Das ist falsch, denn;
- Gemäß SRT wird der Abstand s zweier Objekte nach Raum und Zeit gemessen über die sog. Minkowski-Metrik, die den üblichen Abstandsbegriff im 3-dimensionalen euklidischen Raum in die Zeitdimension hinein verallgemeinert:
- ds2 = c2dt2 – ( dx2 + dy2 + dz2 )
- Hier steht c für die im 3-dimensionalen Raum beobachtete Lichtgeschwindigkeit.
- Ignoriert man in 4-dimensionalen Vektoren die Zeitkomponente, so reduziert das unser Raum-Zeit-Gefüge auf einen 3-dimensionalen Raum. Insbesondere wird hierdurch jede Geschwindigkeit durch den 4-dimensionalen Raum auf den durch uns beobachtbaren Geschwindigkeitsanteil durch den 3-dimensionalen Raum projeziert.
- Wendet man obige Formal für ds2 auf Photonen an (aufs Licht also), so zeigt sie, dass
- Licht sich niemals durch die Zeit bewegt und
- jeder sich nur durch die Zeit bewegende Körper dort Lichtgeschwindigkeit hat.
Natürlich zeigt diese Argumentation ganz allgemein:
Gruß, grtgrt
Beitrag 2035-7
Wann ist ein Bezugssystem ein sog. Inertialsystem
Nun, Okotombrok, es geht doch:
wie Henry ganz richtig bemerkt, kann es Sterne geben (und gibt sie wohl auch), die sich — der Expansion des Universums wegen — mit einer Geschwindigkeit auseinander bewegen, die größer als die Lichtgeschwindigkeit ist.
Nun kann man ja ganz sicher jeden dieser beiden Sterne als Ursprung eines Bezugssystems sehen. Da der Begriff "Inertialsystem" offenbar ein SRT-spezifischer ist, wird man diese beiden Systeme nicht Inertialsysteme nennen können. Das aber zeigt ja nur, dass eine allgemeinere Theorie her muss.
FRAGE also: Gibt es eine Theorie, die selbst im Beispiel dieser zwei Sterne noch Aussagen machen kann?
Nebenbei: Auf Einstein online wird definiert:
Nach dieser Definition müssten selbst meine zwei Sterne im Beispiel oben noch ein Inertialsystem begründen. Dass die SRT auf sie nicht anwendbar ist, liegt wohl einfach daran, dass die davon ausgeht, dass sich kein Körper relativ zu einem anderem mit einer Geschwindigkeit höher als c bewegen kann.
Nun: Auch die ART geht davon aus. Warum aber sagen ihre Gleichungen uns dann, dass der Raum sich sehr wohl mit höherer Geschwindigkeit ausdehnen kann?
Bin sehr gespannt auf Deine Antworten,
Gruß, grtgrt
Okotombrok aus 2035-2:Hallo Grtgrt,
der Ursprung eines Inertialsystems muss an irgendetwas "festgemacht" werden, von dem aus beobachtet werden kann.
Zwei Inertialsysteme, die sich mit LG voneinander entfernen, würde bedeuten, zwei Beobachter entfernen sich mit LG voneinander.
Das macht keinen Sinn weil geht nicht.
mfg okotombrok
Nun, Okotombrok, es geht doch:
wie Henry ganz richtig bemerkt, kann es Sterne geben (und gibt sie wohl auch), die sich — der Expansion des Universums wegen — mit einer Geschwindigkeit auseinander bewegen, die größer als die Lichtgeschwindigkeit ist.
Nun kann man ja ganz sicher jeden dieser beiden Sterne als Ursprung eines Bezugssystems sehen. Da der Begriff "Inertialsystem" offenbar ein SRT-spezifischer ist, wird man diese beiden Systeme nicht Inertialsysteme nennen können. Das aber zeigt ja nur, dass eine allgemeinere Theorie her muss.
FRAGE also: Gibt es eine Theorie, die selbst im Beispiel dieser zwei Sterne noch Aussagen machen kann?
Nebenbei: Auf Einstein online wird definiert:
Zitat:Ein Inertialsystem ist ein Bezugssystem, in dem das Trägheitsgesetz der Mechanik gilt:
Körper, auf die keine Kräfte wirken, befinden sich in Ruhe oder laufen mit konstanter Geschwindigkeit auf geraden Bahnen.
Nach dieser Definition müssten selbst meine zwei Sterne im Beispiel oben noch ein Inertialsystem begründen. Dass die SRT auf sie nicht anwendbar ist, liegt wohl einfach daran, dass die davon ausgeht, dass sich kein Körper relativ zu einem anderem mit einer Geschwindigkeit höher als c bewegen kann.
Nun: Auch die ART geht davon aus. Warum aber sagen ihre Gleichungen uns dann, dass der Raum sich sehr wohl mit höherer Geschwindigkeit ausdehnen kann?
Bin sehr gespannt auf Deine Antworten,
Gruß, grtgrt
Beitrag 2032-54
-
Hallo Hans-m,
das ist ganz richtig: Inertialsysteme existieren nur in der Theorie.
Genauer: Die SRT ist nur auf Inertialsysteme anwendbar, die aber existieren real nur annähernd (und so werden die Aussagen der SRT auf real Existierendes angewandt eben auch nur annähernd das beschreiben, was wirklich passiert).
Gruß, grtgrt
Hans-m aus 2032-51:
Jedes Objekt, dass sich irgend wo im Universum befindet, unterliegt der Gravitation, mal mehr, mal weniger, je nachdem wie viel Masse sich in der Umgebung befindet. Nach [dieser� Definition gäbe es überhaupt keine Inertialsysteme.
Hallo Hans-m,
das ist ganz richtig: Inertialsysteme existieren nur in der Theorie.
Genauer: Die SRT ist nur auf Inertialsysteme anwendbar, die aber existieren real nur annähernd (und so werden die Aussagen der SRT auf real Existierendes angewandt eben auch nur annähernd das beschreiben, was wirklich passiert).
Gruß, grtgrt
Beitrag 2035-29
Zwei Klarstellungen
Hallo Henry,
ich habe mir erlaubt, zwei deiner Feststellungen in das Glossar der Arbeitsplattform SRT in der nachstehenden Form einzubringen:
M.f.G. Eugen Bauhof
Wichtig zu wissen ist auch:
Die Aussage "Wenn wir laufen, während ein anderer Mensch still steht, dann vergeht auch für uns die Zeit langsamer, aber halt extrem wenig" ist falsch.
Henry aus 2035-27:Einige Grundlagen sollten mal wieder ins Gedächtnis gerufen werden!
Hallo Henry,
ich habe mir erlaubt, zwei deiner Feststellungen in das Glossar der Arbeitsplattform SRT in der nachstehenden Form einzubringen:
Zitat:Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
M.f.G. Eugen Bauhof
Wichtig zu wissen ist auch:
Die Aussage "Wenn wir laufen, während ein anderer Mensch still steht, dann vergeht auch für uns die Zeit langsamer, aber halt extrem wenig" ist falsch.
-
Es ist lediglich so, dass es der Laufende den Eindruck hat, die Uhr einer stehenden Person würde langsamer gehen als seine eigene (wenn er von ihr weg läuft).
Umgekehrt hat die stehende Person den Eindruck, die Uhr eines Läufers würde langsamer gehen als die eigene, solange er sich entfernt (bzw. schneller gehen, wenn der Laufende näher kommt).
In Wirklichkeit aber altern beide gleich schnell (solange sie nicht unterschiedlich stark beschleunigt sind).
Beitrag 2035-59
-
Frage an dich, Okotombrok:
Da die Geschwindigkeiten v1 und v2 in der Formel deines Beitrags 2035-25 nur Zahlen zu sein scheinen (statt 3-dim Vektoren), stellt sich mir die Frage:
Wie addiert die SRT Geschwindigkeiten, die — ihrer Richtung nach —
Anders gefragt: Wie lautet die Formel der SRT, mit der man Geschwindigkeiten beliebiger Richtung (Geschwindigkeitsvektoren) addiert?
Gruß,
grtgrt
Frage an dich, Okotombrok:
Da die Geschwindigkeiten v1 und v2 in der Formel deines Beitrags 2035-25 nur Zahlen zu sein scheinen (statt 3-dim Vektoren), stellt sich mir die Frage:
Wie addiert die SRT Geschwindigkeiten, die — ihrer Richtung nach —
- senkrecht aufeinander stehen
- oder deren Richtung einen spitzen oder stumpfen Winkel zwischen sich hat?
Anders gefragt: Wie lautet die Formel der SRT, mit der man Geschwindigkeiten beliebiger Richtung (Geschwindigkeitsvektoren) addiert?
Gruß,
grtgrt
Beitrag 2035-70
Lese Eckhard Rebhans Buch zur SRT
Hallo Grtgrt,
das habe ich bisher nur in einem einzigen Buch gesehen (bei Eckhard Rebhan). Da muss man die Lorentz-Transformationen vektoriell herleiten. Das ist (auch für mich) sehr kompliziert. Das sollten wir lieber lassen. Oder benötigst du es unbedingt? Für was?
M.f.G. Eugen Bauhof�
Grtgrt aus 2035-59:Wie addiert die SRT Geschwindigkeiten, die — ihrer Richtung nach senkrecht aufeinander stehen oder deren Richtung einen spitzen oder stumpfen Winkel zwischen sich hat? Anders gefragt: Wie lautet die Formel der SRT, mit der man Geschwindigkeiten beliebiger Richtung (Geschwindigkeitsvektoren) addiert?
Hallo Grtgrt,
das habe ich bisher nur in einem einzigen Buch gesehen (bei Eckhard Rebhan). Da muss man die Lorentz-Transformationen vektoriell herleiten. Das ist (auch für mich) sehr kompliziert. Das sollten wir lieber lassen. Oder benötigst du es unbedingt? Für was?
M.f.G. Eugen Bauhof�
Beitrag 2035-73
-
Hallo Gebhard,
hier ist das Buch:
Rebhan, Eckhard
Theoretische Physik.
Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999. ISBN=3-8274-0246-8
M.f.G. Eugen Bauhof�
Grtgrt aus 2035-72:...werde mal versuchen, das Buch zu finden. Meine Frage ist zunächst reine Neugier.
Hallo Gebhard,
hier ist das Buch:
Rebhan, Eckhard
Theoretische Physik.
Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999. ISBN=3-8274-0246-8
M.f.G. Eugen Bauhof�
Beitrag 2035-113
-
Nachdem v = c Grenzfall von v < c ist ( und die Formel für alle v < c gilt ), gilt sie mit Sicherheit auch für v = c .
Bauhof aus 2035-104:
Die Formel aus Beitrag 2035-25 für die Geschwindigkeitsaddition ist korrekt, aber ich bezweifle, dass sie auch für v=c aussagekräftig ist. Warum? Weil die Geschwindigkeitsadditions-Formel aus der Lorentz-Transformation hergeleitet wurde und diese gilt nur für Relativgeschwindigkeiten v<c.
Beitrag 2035-62
Geschwindigkeit ist Ortsveränderung — nicht Vergrößerung von Abstand !!!
Hallo Stueps,
bis vor kurzem verstand ich unter "Geschwindigkeit" u.A. auch das "Ausmaß, in dem sich Abstand pro Zeiteinheit verändert".
Das aber scheint falsch zu sein. Man muss darunter "Ortsveränderung pro Zeiteinheit" verstehen. Die Lichtgeschwindigkeit ist dann nichts anders als
die maximale Geschwindigkeit, mit der sich eine Wellenfront ausbreiten kann.
Beispiel: Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle,
Mit besten Grüßen,
grtgrt
Stueps aus 2035-57:
Auf die Möglichkeit des Informationsaustausches kommt es also vielleicht nicht unbedingt an.
Ich ahne, dass sich dieser Gedankengang noch ausbauen lässt, ich hoffe, mir fällt dazu noch etwas ein.
Was meint ihr dazu?
Hallo Stueps,
bis vor kurzem verstand ich unter "Geschwindigkeit" u.A. auch das "Ausmaß, in dem sich Abstand pro Zeiteinheit verändert".
Das aber scheint falsch zu sein. Man muss darunter "Ortsveränderung pro Zeiteinheit" verstehen. Die Lichtgeschwindigkeit ist dann nichts anders als
Beispiel: Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle,
- deren Radius sich mit 299 752 458 m/sec vergrößert.
- Ihr Durchmesser aber vergrößert sich d o p p e l t so schnell (und das ist kein Widerspruch zur SRT, da die Rate, mit der sich ein A b s t a n d vergrößert, nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann).
Mit besten Grüßen,
grtgrt
Beitrag 2035-71
-
Hallo zusammen,
ein weiteres Beispiel dafür, dass die Rate, mit der sich ein Abstand vergrößert nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann, ist die Universum-Expansion.
Wenn die Expansionsrate so groß ist, dass von einer Galaxie A zur Galaxie B kein Lichtstrahl mehr gelangen kann, dann liest man oft, A und B fliehen voneinander mit Überlichtgeschwindigkeit.
Die Wahrheit ist, dass die Galaxien stillstehen und nur der Raum dazwischen dehnt sich aus, was dann eine Abstandsvergrößerung zur Folge hat. Ein Lichtstrahl von A nach B "verhungert", weil die Abstandsvergrößerung schneller erfolgt, als das Licht folgen kann.
M.f.G. Eugen Bauhof�
ein weiteres Beispiel dafür, dass die Rate, mit der sich ein Abstand vergrößert nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann, ist die Universum-Expansion.
Wenn die Expansionsrate so groß ist, dass von einer Galaxie A zur Galaxie B kein Lichtstrahl mehr gelangen kann, dann liest man oft, A und B fliehen voneinander mit Überlichtgeschwindigkeit.
Die Wahrheit ist, dass die Galaxien stillstehen und nur der Raum dazwischen dehnt sich aus, was dann eine Abstandsvergrößerung zur Folge hat. Ein Lichtstrahl von A nach B "verhungert", weil die Abstandsvergrößerung schneller erfolgt, als das Licht folgen kann.
M.f.G. Eugen Bauhof�
Beitrag 2035-84
Bezugssysteme, die sich mit Lichtgeschwindigkeit zueinander bewegen
Hallo Hans,
dass die Geschwindigkeit genau c ist, kann nicht die Ursache sein, denn:
Da c die Lichtgeschwindigkeit im Vakuum ist, nehme ich an, dass das Licht sich durch Glas etwa mit etwas geringerer Geschwindigkeit v bewegt. Wenigstens dann also müssten die Formeln der SRT doch anwendbar sein.
Das aber bedeutet, dass sie auch im Grenzfall v gegen c anwendbar sind, w e n n der Limes rein mathematisch existiert.
Der wirkliche Grund, warum die Formeln auf unser Beispiel nicht anwendbar sind, muss demnach ein anderer sein:
Würden wir unter den — als Teilchen so natürlich gar nicht existierenden — Objekten Beobachter verstehen, die von der Lichtwelle vor sich her geschoben würden, müsste aus deren Sicht (nach meiner eben vorgebrachten Argumentation) ihre Relativgeschwindigkeit wirklich c — und nicht 2c — sein.
Dass dem nicht so ist, erkläre ich mir das so:
Die SRT beschreibt, mit welcher Geschwindigkeit sich die B e o b a c h t e r gegeneinander bewegt sehen.
In dem Fall aber sehen die beiden Beobachter einander gar nicht ( und so ist hier die SRT eben nicht anwendbar ).
Gruß, grtgrt
Hans-m aus 2035-82:Zurück zu Bauhofs Beispiel:
Der neutrale Beobachter "sieht" dass beide Lichtteilchen nach 1 Sekunde 2 Lichtsekunden voneinander entfernt sind, und somit eine Geschwindigkeitsdifferenz von 2 C zwischen beiden besteht.
Da aber Licht selbst nicht als Bezugsystem definiert werden darf (so zumindest wurde es hier mehrfach gepostet) kann ich nicht behaupten, dass aus Sicht von Lichtteilchen 1 das Lichtteilchen 2 eine Geschwindigkeit von 2 C hat.
Oder liege ich hier falsch?
Hallo Hans,
dass die Geschwindigkeit genau c ist, kann nicht die Ursache sein, denn:
Da c die Lichtgeschwindigkeit im Vakuum ist, nehme ich an, dass das Licht sich durch Glas etwa mit etwas geringerer Geschwindigkeit v bewegt. Wenigstens dann also müssten die Formeln der SRT doch anwendbar sein.
Das aber bedeutet, dass sie auch im Grenzfall v gegen c anwendbar sind, w e n n der Limes rein mathematisch existiert.
Der wirkliche Grund, warum die Formeln auf unser Beispiel nicht anwendbar sind, muss demnach ein anderer sein:
Würden wir unter den — als Teilchen so natürlich gar nicht existierenden — Objekten Beobachter verstehen, die von der Lichtwelle vor sich her geschoben würden, müsste aus deren Sicht (nach meiner eben vorgebrachten Argumentation) ihre Relativgeschwindigkeit wirklich c — und nicht 2c — sein.
Dass dem nicht so ist, erkläre ich mir das so:
In dem Fall aber sehen die beiden Beobachter einander gar nicht ( und so ist hier die SRT eben nicht anwendbar ).
Gruß, grtgrt
Beitrag 2035-87
-
Hallo Stueps,
Photonen sind keine Teilchen, die durch den Raum sausen. Es sind Wellen, die sich ausbreiten, und die sich nur dort, wo sie mit einer Messvorrichtung oder einem anderem Wellenpaket interagieren, als Teilchen "verkleidet" zeigen.
Was Du mit deinen "Photonen" also wirklich meinst, sind Beobachter, die sich immer genau dort befinden, wo die Wellenfront sich befindet (Beobachter, die — wie ich in Beitrag 2035-84 sage — von der Welle "vor ihr hergeschoben" werden).
Kurz: Beitrag 2035-84 beantwortet deine Frage insofern, als er dir sagen soll:
Gruß, grtgrt
Stueps aus 2035-77:
Wenn Photonen physikalische Objekte im Sinne der SRT sind, dann müsste für sie das Gleiche gelten, wie für zwei entsprechende Raumschiffe:
Diese fliegen von uns entgegengesetzt mit 0,9c los. Aus unserer Sicht sind sie dann nach einer Sekunde voneinander 1,8 Ls entfernt. Aus Sicht der jeweiligen Raumschiffbesatzung jedoch ist das andere Raumschiff nach einer Sekunde nur (ungefähr) 0,94 Ls entfernt.
Oder?
Hallo Stueps,
Photonen sind keine Teilchen, die durch den Raum sausen. Es sind Wellen, die sich ausbreiten, und die sich nur dort, wo sie mit einer Messvorrichtung oder einem anderem Wellenpaket interagieren, als Teilchen "verkleidet" zeigen.
Was Du mit deinen "Photonen" also wirklich meinst, sind Beobachter, die sich immer genau dort befinden, wo die Wellenfront sich befindet (Beobachter, die — wie ich in Beitrag 2035-84 sage — von der Welle "vor ihr hergeschoben" werden).
Kurz: Beitrag 2035-84 beantwortet deine Frage insofern, als er dir sagen soll:
- Ja, Du hast im Prinzip recht,
- aber wo Beobachter sich gegeneinander ebenso schnell bewegen wie das Licht (sei es im Vakuum oder im Glas), macht die SRT gar keine Aussage — sie ist nur anwendbar auf Initialsysteme, die sich relativ zueinander langsamer als das Licht bewegen (so dass Information über den einen den anderen erreichen kann).
Gruß, grtgrt
Beitrag 2035-92
-
Hallo Stueps,
für Photonen gilt nicht das gleiche wie für Raumschiffe. Ich kann da nur Grtgrt zustimmen, wenn er schreibt:
M.f.G. Eugen Bauhof�
Stueps aus 2035-77:Wenn Photonen physikalische Objekte im Sinne der SRT sind, dann müsste für sie das Gleiche gelten, wie für zwei entsprechende Raumschiffe...
Hallo Stueps,
für Photonen gilt nicht das gleiche wie für Raumschiffe. Ich kann da nur Grtgrt zustimmen, wenn er schreibt:
Zitat:...aber wo Beobachter sich gegeneinander ebenso schnell bewegen wie das Licht (sei es im Vakuum oder im Glas), macht die SRT gar keine Aussage — sie ist nur anwendbar auf Initialsysteme, die sich relativ zueinander langsamer als das Licht bewegen (so dass Information über den einen den anderen erreichen kann).
M.f.G. Eugen Bauhof�
Beitrag 2035-96
-
Völlig richtig — das sehe ich auch so.
Henry aus 2035-89:Systeme, die sich mit Lichtgeschwindigkeit zueinander bewegen, können keine Information austauschen.
Es ist außerdem völlig sinnlos, nach einer Längenkontraktion oder Zeitdilatation in solchen Systemen zu fragen.
Völlig richtig — das sehe ich auch so.
Beitrag 1985-288
-
Hallo Henry,
wie ich in Beitrag 2035-113 und Beitrag 2035-84 schon sagte, bin auch ich der Meinung, dass die Formel sich auch noch auf den Fall v1 = v2 = c anwenden lässt — aber eben NUR aus der Sicht der beiden "Photonen".
Aus Sicht der punktförmigen Lichtquelle kann man v1 und v2 so aber NICHT addieren.
Die SRT beschäftigt sich halt stets nur mit 2 (statt 3) gegeneinander bewegter Beobachter.
Gruß, grtgrt
Henry aus 1985-287:
Die Geschwindigkeiten v von Photonen, die sich entgegengesetzt voneinander entfernen, lassen mit der Formel aus obigem Theorem addieren. Ihre Geschwindigkeiten betragen – genau, wie gefordert – für jedes Photon aus der jeder Sicht c. Photonen SIND physikalische Objekte, und wenn sie sich voneinander entfernen, lassen sich ihre Geschwindigkeiten wie beschrieben addieren.
Hallo Henry,
wie ich in Beitrag 2035-113 und Beitrag 2035-84 schon sagte, bin auch ich der Meinung, dass die Formel sich auch noch auf den Fall v1 = v2 = c anwenden lässt — aber eben NUR aus der Sicht der beiden "Photonen".
Aus Sicht der punktförmigen Lichtquelle kann man v1 und v2 so aber NICHT addieren.
Die SRT beschäftigt sich halt stets nur mit 2 (statt 3) gegeneinander bewegter Beobachter.
Gruß, grtgrt
Beitrag 1985-290
-
Doch, Henry, das ist richtig, denn
Gruß, grtgrt
PS: Was all das damit zu tun haben soll, dass Elektronen eines Atoms von einem Energieniveau in ein anderes springen können (ein Übergang, der keine Zeit kostet), verstehe ich nicht.
Henry aus 1985-289:
Das ist nicht richtig!
Doch, Henry, das ist richtig, denn
- die Aussage, dass der Radius einer elektromagnetischen Kugelwelle sich mit Lichtgeschwindigkeit vergrößert ist äquivalent zur Aussage, dass ihr Durchmesser sich mit der doppelten Rate vergrößert.
- Das aber bedeutet NICHT, dass sich da irgendetwas schneller als das Licht bewegt.
Gruß, grtgrt
PS: Was all das damit zu tun haben soll, dass Elektronen eines Atoms von einem Energieniveau in ein anderes springen können (ein Übergang, der keine Zeit kostet), verstehe ich nicht.
Beitrag 1985-296
-
Da bin ich völlig anderer Ansicht:
Wo immer eine Welle entsteht, ist sie Kugelwelle bis hin zu dem Punkt, an dem sie mit einer anderen zusammenstößt (die beiden verschmelzen und teilen sich neu auf in mehrere Wellen, deren Lebenszyklus ebenso verläuft). Mit anderen Worten: Sie verschmelzen zu einem Wellenpaket.
Die Tatsache, dass — mindestens der Quantenfluktuation wegen — ständig neue Wellen entstehen, hat zur Folge, dass es entsprechend oft Zusammenstöße von Wellen gibt. Wo immer ein solcher Zusammenstoß passiert, denken wir, ein Teilchen zu sehen (z.B. ein Photon). Was wir da sehen, ist aber nur Strahlung, die als Ergebnis des Zusammenstoßes entsteht. Allgemeiner:
Was wir wahrnehmen, ist F o l g e so eines Zusammenstoßes (z.B. die Reaktion unseres Gehirns auf den Zusammenstoß einer Lichtwelle mit unserem Auge).
Solche Folge ist W i r k u n g , und da Wirkung gequantelt ist, denken wir, ein "Teilchen" registriert zu haben.
Zudem sollte man sich klar machen, dass das, was wir sehen bzw. was unsere Messgeräte registrieren i.A. ganze Wellenpakete sind.
Eine stehende Welle etwa kann als Überlagerung zweier gegenläufig fortschreitender Wellen gleicher Frequenz und gleicher Amplitude aufgefasst werden.
Während jede Welle Sinusform hat, kann ein Wellenpaket praktisch jeden Funktionsgraphen darstellen (z.B. einen recht schmalen Peak, der steht oder sich gleichförmig, mit beliebig kleiner Geschwindigkeit, maximal aber mit Lichtgeschwindigkeit, voranbewegt).
Mathematisch gesehen ist jedes Wellenpaket Linearkombination von Produkten aus Funktionen, deren jede eine Welle darstellt.
Jede Welle beschreibt gleichförmige Potentialschwankung eines Feldes.
Jedes Wellenpaket ist Überlagerung von Wellen in diesem Sinne.
Wo Wellenpakete umkonfiguriert werden, glauben wir Teilchen (oder Zerfallsprodukte davon) zu sehen,
obgleich wir in Wirklichkeit nur Stellen verfolgen, an denen — als Abfallprodukt — elektromagnetische Strahlung entsteht.
Was die Quantenphysik entdeckt hat, war u.A. auch die Tatsache, dass, wo die Frequenz einer Welle sich ändert, das nicht stetig geschieht, sondern nur in einem gewissen Raster. Die Stringtheorie interpretiert das so, dass der "String", der da schwingt, gewisse Länge hat. Da sie stets nur ganzzahliges Vielfaches der Wellenlänge sein kann, ist es nicht möglich, dass der String in jeder beliebigen Frequenz schwingt. Die Frequenz, in der er schwingt, kann sich aber spontan ändern (es ist ihm keineswegs nur eine Frequenz möglich).
Henry aus 1985-295:
... die Kugelwelle, die du ansprichst, ein ganz spezieller und idealisierter Sonderfall ist und mit dem, was gewöhnlich physikalisch geschieht, nichts zu tun hat.
Photonen, die im normalen, physikalischen Leben erzeugt werden, bewegen sich nicht wie eine Kugelwelle, um es deutlicher zu sagen.
Da bin ich völlig anderer Ansicht:
Wo immer eine Welle entsteht, ist sie Kugelwelle bis hin zu dem Punkt, an dem sie mit einer anderen zusammenstößt (die beiden verschmelzen und teilen sich neu auf in mehrere Wellen, deren Lebenszyklus ebenso verläuft). Mit anderen Worten: Sie verschmelzen zu einem Wellenpaket.
Die Tatsache, dass — mindestens der Quantenfluktuation wegen — ständig neue Wellen entstehen, hat zur Folge, dass es entsprechend oft Zusammenstöße von Wellen gibt. Wo immer ein solcher Zusammenstoß passiert, denken wir, ein Teilchen zu sehen (z.B. ein Photon). Was wir da sehen, ist aber nur Strahlung, die als Ergebnis des Zusammenstoßes entsteht. Allgemeiner:
Solche Folge ist W i r k u n g , und da Wirkung gequantelt ist, denken wir, ein "Teilchen" registriert zu haben.
Zudem sollte man sich klar machen, dass das, was wir sehen bzw. was unsere Messgeräte registrieren i.A. ganze Wellenpakete sind.
Eine stehende Welle etwa kann als Überlagerung zweier gegenläufig fortschreitender Wellen gleicher Frequenz und gleicher Amplitude aufgefasst werden.
Während jede Welle Sinusform hat, kann ein Wellenpaket praktisch jeden Funktionsgraphen darstellen (z.B. einen recht schmalen Peak, der steht oder sich gleichförmig, mit beliebig kleiner Geschwindigkeit, maximal aber mit Lichtgeschwindigkeit, voranbewegt).
Jede Welle beschreibt gleichförmige Potentialschwankung eines Feldes.
Jedes Wellenpaket ist Überlagerung von Wellen in diesem Sinne.
Wo Wellenpakete umkonfiguriert werden, glauben wir Teilchen (oder Zerfallsprodukte davon) zu sehen,
obgleich wir in Wirklichkeit nur Stellen verfolgen, an denen — als Abfallprodukt — elektromagnetische Strahlung entsteht.
Was die Quantenphysik entdeckt hat, war u.A. auch die Tatsache, dass, wo die Frequenz einer Welle sich ändert, das nicht stetig geschieht, sondern nur in einem gewissen Raster. Die Stringtheorie interpretiert das so, dass der "String", der da schwingt, gewisse Länge hat. Da sie stets nur ganzzahliges Vielfaches der Wellenlänge sein kann, ist es nicht möglich, dass der String in jeder beliebigen Frequenz schwingt. Die Frequenz, in der er schwingt, kann sich aber spontan ändern (es ist ihm keineswegs nur eine Frequenz möglich).
Beitrag 2089-21
-
Nein, auch nicht ein ganz klein bisschen, denn:
Die Raumzeit der SRT ist ein 4-dimensionaler Vektorraum, Abstände darin sind über die Minkoski-Metrik definiert, und in deren Definition gehen Begriffe wie Beobachter und Inertialsystem ja gar nicht ein.
Richtig aber ist deine Aussage, dass in der SRT jeder Beobachter einen eigenen Maßstab hat, und diese Maßstäbe eben nicht übereinstimmen, da — der Endlichkeit der Lichtgeschwindigkeit wegen — kein Ereignis von zwei zueinander bewegten Beobachtern zum selben Zeitpunkt (im Sinne des 4-dimensionalen Raumes und seiner Metrik) wahrgenommen wird.
Die Unterschiede in den beobachterspezifischen S i c h t e n (die Unterschiede der Maßstäbe also) kommen dadurch zustande, dass jeder Beobachter davon ausgeht, das Ereignis trete ein, wenn e r es eintreten sieht. In Wirklichkeit ist es aber schon vorher eingetreten, da die Signalgeschwindigkeit endlich ist.
Die Zeitdifferenz, um die es hier geht, ist proportional zum Abstand der sich beobachtenden Objekte. Sie wächst, wenn der Abstand sich vergrößert, und sie schrumpft, wenn er sich verkleinert.
Gruß, grtgrt
Nein, auch nicht ein ganz klein bisschen, denn:
Die Raumzeit der SRT ist ein 4-dimensionaler Vektorraum, Abstände darin sind über die Minkoski-Metrik definiert, und in deren Definition gehen Begriffe wie Beobachter und Inertialsystem ja gar nicht ein.
Richtig aber ist deine Aussage, dass in der SRT jeder Beobachter einen eigenen Maßstab hat, und diese Maßstäbe eben nicht übereinstimmen, da — der Endlichkeit der Lichtgeschwindigkeit wegen — kein Ereignis von zwei zueinander bewegten Beobachtern zum selben Zeitpunkt (im Sinne des 4-dimensionalen Raumes und seiner Metrik) wahrgenommen wird.
Die Unterschiede in den beobachterspezifischen S i c h t e n (die Unterschiede der Maßstäbe also) kommen dadurch zustande, dass jeder Beobachter davon ausgeht, das Ereignis trete ein, wenn e r es eintreten sieht. In Wirklichkeit ist es aber schon vorher eingetreten, da die Signalgeschwindigkeit endlich ist.
Die Zeitdifferenz, um die es hier geht, ist proportional zum Abstand der sich beobachtenden Objekte. Sie wächst, wenn der Abstand sich vergrößert, und sie schrumpft, wenn er sich verkleinert.
Gruß, grtgrt
Beitrag 2089-29
-
Hallo H...,
interessant ist, dass es im Raum (der SRT) global einheitliche Zeit gibt.
So erinnert uns etwa Josef Honerkamp auf Seite 224-225 seines Buches Die Entdeckung des Unvorstellbaren (Spektrum Verlag, 2009) daran, dass noch Einstein selbst einen Algorithmus angegeben hat, die Uhren sämtlicher Orte im Raum zu synchronisieren:
Gruß, grtgrt
Hallo H...,
interessant ist, dass es im Raum (der SRT) global einheitliche Zeit gibt.
So erinnert uns etwa Josef Honerkamp auf Seite 224-225 seines Buches Die Entdeckung des Unvorstellbaren (Spektrum Verlag, 2009) daran, dass noch Einstein selbst einen Algorithmus angegeben hat, die Uhren sämtlicher Orte im Raum zu synchronisieren:
Zitat von Honerkamp:
Die Bewegung eines Bezugssystems relativ zum anderen verursacht ... unterschiedliche Auffassung von Gleichzeitigkeit. Bleibt man in einem einzigen Bezugssystem, so kann man schon den Begriff der Gleichzeitigkeit einen Sinn geben; man könnte überall Uhren aufhängen und diese synchronisieren. Einstein hat eine einfache Vorschrift für die Synchonisation zweier Uhren angegeben:
Man schicke, wenn die Uhr A die Zeit t1 anzeigt, einen Lichstrahl von ihr nach Uhr B, dieser werde reflektiert und komme zur Zeit t2 zur Uhr A zurück.
Unterstellt man, dass die Laufzeit dt des Lichtes von A nach B die gleiche ist wie die von B nach A, so ist dt = ( t2 – t1 )/2 , und muss man die Uhr B nur so einstellen, dass die Zeit t1 + dt = ( t1 + t2 )/2 anzeigt, wenn der Lichtstrahl bei ihr ankommt.
Gruß, grtgrt
Beitrag 2089-31
-
Hallo Henry,
es wird ja auch nicht behauptet, dass es für a l l e Beobachter einen einheitlichen Zeitbegriff gäbe. Er existiert aber durchaus, wenn man nur ein einziges Bezugssystem betrachtet. (Zur Erinnerung: Der zweite Satz Honerkamps beginnt mit einer wichtigen Voraussetzung. Er lautet nämlich: "Bleibt man in einem einzigen Bezugssystem, so kann man schon dem Begriff der Gleichzeitigkeit einen Sinn geben ...").
Und das obgleich dem nicht so ist über mehrere Bezugssysteme hinweg, was Honerkamp ja auch feststellt:
In diesem Unterschied kommt halt wieder sehr schön zum Ausdruck, dass Gegenstand der SRT eben nicht die S t r u k t u r der Raumzeit ist, sondern nur, wie sich die
S i c h t e n unterschiedlicher Beobachter unterscheiden, w e n n jene Beobachter relativ zueinander (gleichförmig) bewegt sind.
Bitte auch beachten: Während die ART kein einziges Bezugssystem kennt, welches den gesamten Raum zum Gegenstand hat, ist in der SRT j e d e s Bezugssystem eines für den gesamten Raum.
Gruß, grtgrt
Henry in 2089-30:
Gebhard, wenn es eine einheitliche Zeit gäbe, müsste man die Uhren nicht synchronisieren.
Hallo Henry,
es wird ja auch nicht behauptet, dass es für a l l e Beobachter einen einheitlichen Zeitbegriff gäbe. Er existiert aber durchaus, wenn man nur ein einziges Bezugssystem betrachtet. (Zur Erinnerung: Der zweite Satz Honerkamps beginnt mit einer wichtigen Voraussetzung. Er lautet nämlich: "Bleibt man in einem einzigen Bezugssystem, so kann man schon dem Begriff der Gleichzeitigkeit einen Sinn geben ...").
Und das obgleich dem nicht so ist über mehrere Bezugssysteme hinweg, was Honerkamp ja auch feststellt:
Zitat von Honerkamp, S. 224:
Im Rahmen der Speziellen Relativitätstheorie gibt es kein universelles Jetzt, keine Weltuhr, die im gesamten Universum die Zeit angibt und damit keine Einigung über Gleichzeitigkeit von räumlich getrennten Ereignissen für alle Beobachter, wie immer sie sich auch bewegen.
In diesem Unterschied kommt halt wieder sehr schön zum Ausdruck, dass Gegenstand der SRT eben nicht die S t r u k t u r der Raumzeit ist, sondern nur, wie sich die
S i c h t e n unterschiedlicher Beobachter unterscheiden, w e n n jene Beobachter relativ zueinander (gleichförmig) bewegt sind.
Bitte auch beachten: Während die ART kein einziges Bezugssystem kennt, welches den gesamten Raum zum Gegenstand hat, ist in der SRT j e d e s Bezugssystem eines für den gesamten Raum.
Gruß, grtgrt
Beitrag 2089-34
Einsteins Uhrensynchronisation — und eine Frage dazu
Hallo Henry,
vielleicht reden wir ja nur aneinander vorbei. Ich sehe es wie folgt:
Nach Einsteins Definition (1905) wird zum Zeitpunkt t1 ein Lichtsignal von Uhr 1 zur Uhr X gesandt, die dann sofort — beispielsweise durch einen Spiegel — ein Lichtsignal zurücksendet; dieses erreiche Uhr 1 zum Zeitpunkt tX .
Die Einstein-Synchronisation besteht nun darin, Uhr X so zu stellen, dass der Zeitpunkt der Reflexion ( t1 + tX )/2 ist.
Wenn wir uns jetzt vorstellen. dass die Quelle des von Uhr 1 ausgehenden Lichtsignals eine punktförmige Lichtquelle ist, breitet sich das Signal als kugelförmige elektromagnetische Welle aus, erreicht also a l l e Uhren X im gesamten 3-dimensionalen Raum. Eingestellt nach Einsteins Regel, sind dann also a l l e Uhren im Raum zu Uhr 1 synchron.
Warum bitte soll man das dann nicht als einen global einheitlichen Zeitbegriff sehen können
( nutzbar durch alle, die dasselbe Bezugssystem wie Uhr 1 nutzen )?
Gruß, grtgrt
Henry in 2089-32:
Ich darf dich zitieren: "interessant ist, dass es im Raum (der SRT) global einheitliche Zeit gibt." Du redest also nicht von einem einheitlichen Zeitbegriff, sondern von einheitlicher Zeit. ... Du argumentierst vollkommen inkonsequent und unlogisch. Es gibt immer nur zwei Beobachter, die sich miteinander auf Gleichzeitigkeit einigen können, für alle anderen Beobachter ist das jeweils aufs Neue zu bestimmen. Hat sich was mit einer globalen Zeit.
Hallo Henry,
vielleicht reden wir ja nur aneinander vorbei. Ich sehe es wie folgt:
Nach Einsteins Definition (1905) wird zum Zeitpunkt t1 ein Lichtsignal von Uhr 1 zur Uhr X gesandt, die dann sofort — beispielsweise durch einen Spiegel — ein Lichtsignal zurücksendet; dieses erreiche Uhr 1 zum Zeitpunkt tX .
Die Einstein-Synchronisation besteht nun darin, Uhr X so zu stellen, dass der Zeitpunkt der Reflexion ( t1 + tX )/2 ist.
Wenn wir uns jetzt vorstellen. dass die Quelle des von Uhr 1 ausgehenden Lichtsignals eine punktförmige Lichtquelle ist, breitet sich das Signal als kugelförmige elektromagnetische Welle aus, erreicht also a l l e Uhren X im gesamten 3-dimensionalen Raum. Eingestellt nach Einsteins Regel, sind dann also a l l e Uhren im Raum zu Uhr 1 synchron.
( nutzbar durch alle, die dasselbe Bezugssystem wie Uhr 1 nutzen )?
Gruß, grtgrt
Beitrag 2089-35
-
Hallo Grtgrt,
Einsteins Uhrensynchronisation hat überhaupt nichts mit einem "global einheitlichen Zeitbegriff" zu tun.
Alle Uhren im gesamten 3-dimensionalen Raum können zwar erreicht werden, aber nicht alle zur gleichen Zeit, denn das Signal braucht verschiedene Zeiten, bis es alle Uhren erreicht hat. Es sei denn, dass sich alle übrigen Uhren genau auf einer Oberfläche einer 3-D-Kugel befinden. Und im Mittelpunkt der Kugel befände sich Uhr 1.
M.f.G. Eugen Bauhof�
Grtgrt in 2089-34:Wenn wir uns jetzt vorstellen. dass die Quelle des von Uhr 1 ausgehenden Lichtsignals eine punktförmige Lichtquelle ist, breitet sich das Signal als kugelförmige elektromagnetische Welle aus, erreicht also a l l e Uhren X im gesamten 3-dimensionalen Raum. Eingestellt nach Einsteins Regel, sind dann also a l l e Uhren im Raum zu Uhr 1 synchron.
Warum bitte soll man das dann nicht als einen global einheitlichen Zeitbegriff sehen können
( nutzbar durch alle, die dasselbe Bezugssystem wie Uhr 1 nutzen )?
Hallo Grtgrt,
Einsteins Uhrensynchronisation hat überhaupt nichts mit einem "global einheitlichen Zeitbegriff" zu tun.
Alle Uhren im gesamten 3-dimensionalen Raum können zwar erreicht werden, aber nicht alle zur gleichen Zeit, denn das Signal braucht verschiedene Zeiten, bis es alle Uhren erreicht hat. Es sei denn, dass sich alle übrigen Uhren genau auf einer Oberfläche einer 3-D-Kugel befinden. Und im Mittelpunkt der Kugel befände sich Uhr 1.
M.f.G. Eugen Bauhof�
Beitrag 2089-42
Gleichzeitigkeit
Ja, Henry, da kann ich Eugen Bauhof nur aus ganzem Herzen zustimmen.
Bauhof in 2089-40:Hallo Henry,
es ist sinnlos, von der Gleichzeitigkeit von zwei Ereignissen zu sprechen, solange man keine Gleichzeitigkeits-Definition besitzt.
Denn die Gleichzeitigkeit von zwei Ereignissen kann nicht gemessen, sondern nur definiert werden. Dies ist eine Erkenntnis von Einstein. Die Einsteinsche Uhrensynchronisation ist ein Beispiel für eine Definition der Gleichzeitigkeit.
Diese ist aber nicht zwingend, es sind auch andere Definitionen der Gleichzeitigkeit möglich.
Ja, Henry, da kann ich Eugen Bauhof nur aus ganzem Herzen zustimmen.
Beitrag 2089-45
Gleichzeitigkeit aus Sicht einer bestimmten Uhr
Das wiederum sehe ich völlig anders, denn:
Gegeben ein Bezugssystem, in dem sich eine ausgezeichnete Uhr 1 befindet, lässt sich gemäß Einsteins Uhrensynchronisation für jede Stelle X im 3-dimensionalen Raum
d e f i n i e r e n :
Uhrzeit(X) = Uhrzeit(1) – c • A(1,X)
wo c die Lichtgeschwindigkeit bezeichnet, A(1,X) den euklischen Abstand der Stelle X von Uhr 1, und Uhrzeit(1) die von Uhr 1 angezeigte Uhrzeit.
Damit ist — solange man nur dieses eine Bezugssystem nutzt — ganz offensichtlich über die Uhr 1 ein für den gesamten Raum wohdefinierter Zeitbegriff gegeben.
Dieser Zeitbegriff ist übrigens genau der, den wir alle zugrundelegen, wenn wir sagen: Unser Blick auf einen beliebig weit entfernten Himmelskörper zeigt uns diesen Himmelskörper, wie er war, als das Licht, das wir von ihm empfangen, seine Reise von dort hin zu uns angetreten hat: Uhrzeit(X) ist der Zeitpunkt, der aus unserer Sicht (genauer: aus Sicht der Uhr 1) das Ende der Vergangenheit von Stelle X bezeichnet und gleichzeitig den Beginn ihrer noch unbekannten Zukunft.
Einmal mehr wird hier klar, dass sich alle Überlegungen Einsteins, die sich der SRT zuordnen, nur auf beobachterspezifische S i c h t e n beziehen (niemals aber auf Raumstruktur).
Bauhof in 2089-35:Hallo Grtgrt,
Einsteins Uhrensynchronisation hat überhaupt nichts mit einem "global einheitlichen Zeitbegriff" zu tun.
Das wiederum sehe ich völlig anders, denn:
Gegeben ein Bezugssystem, in dem sich eine ausgezeichnete Uhr 1 befindet, lässt sich gemäß Einsteins Uhrensynchronisation für jede Stelle X im 3-dimensionalen Raum
d e f i n i e r e n :
wo c die Lichtgeschwindigkeit bezeichnet, A(1,X) den euklischen Abstand der Stelle X von Uhr 1, und Uhrzeit(1) die von Uhr 1 angezeigte Uhrzeit.
Damit ist — solange man nur dieses eine Bezugssystem nutzt — ganz offensichtlich über die Uhr 1 ein für den gesamten Raum wohdefinierter Zeitbegriff gegeben.
Dieser Zeitbegriff ist übrigens genau der, den wir alle zugrundelegen, wenn wir sagen: Unser Blick auf einen beliebig weit entfernten Himmelskörper zeigt uns diesen Himmelskörper, wie er war, als das Licht, das wir von ihm empfangen, seine Reise von dort hin zu uns angetreten hat: Uhrzeit(X) ist der Zeitpunkt, der aus unserer Sicht (genauer: aus Sicht der Uhr 1) das Ende der Vergangenheit von Stelle X bezeichnet und gleichzeitig den Beginn ihrer noch unbekannten Zukunft.
Einmal mehr wird hier klar, dass sich alle Überlegungen Einsteins, die sich der SRT zuordnen, nur auf beobachterspezifische S i c h t e n beziehen (niemals aber auf Raumstruktur).
Beitrag 2089-47
Selbst Einstein macht gelegentlich eine absolut inhaltsleere Aussage
Hallo Eugen,
wie ich annehme, wolltest Du wohl sagen:
Einsteins Uhrensynchronisation hat überhaupt nichts mit einem global e i n d e u t i g e n (konkurrenzlosen) Zeitbegriff zu tun.
Damit nämlich hättest Du auch nach meinem Verständnis recht.
Gruß, grtgrt
Nebenbei: Wie in Beitrag 2089-45 dargelegt, definiert jeder Ort im Raum einen eigenen, durchaus sinnvollen (Uhr-)Zeitbegriff — aber keine zwei dieser Zeitbegriffe sind identisch. Damit wird sehr schön klar, wie inhaltsleer Einsteins Aussage » Zeit ist, was man von der Uhr abliest « doch eigentlich ist.
Bauhof in 2089-35:Hallo Grtgrt,
Einsteins Uhrensynchronisation hat überhaupt nichts mit einem "global einheitlichen Zeitbegriff" zu tun.
Hallo Eugen,
wie ich annehme, wolltest Du wohl sagen:
Damit nämlich hättest Du auch nach meinem Verständnis recht.
Gruß, grtgrt
Nebenbei: Wie in Beitrag 2089-45 dargelegt, definiert jeder Ort im Raum einen eigenen, durchaus sinnvollen (Uhr-)Zeitbegriff — aber keine zwei dieser Zeitbegriffe sind identisch. Damit wird sehr schön klar, wie inhaltsleer Einsteins Aussage » Zeit ist, was man von der Uhr abliest « doch eigentlich ist.
Beitrag 2068-50
Wie der Beobachter den Zeigerstand einer relativ zu ihm bewegten Uhr errechnet
Du scheinst mir ausweichen zu wollen, Henry, denn:
Mit besten Grüßen,
grtgrt
Henry in 2068-49:
Dein Zitat: » Die beobachterspezifische Sicht ist — per definitionem — stets die, die der Beobachter von seiner eigenen Uhr abliest.
Und das muss auch so sein, da sie sonst ja gar nicht eindeutig wäre (sie würde abhängig vom Objekt, auf dessen Uhr er blickt). «
Lassen wir das Extrem des Photons selbst mal beiseite, es geht hier auch gar nicht in erster Linie um das Photon, sondern darum, dass es bzgl. der Zeitdilatation immer um die Sicht der Uhr aus einem System heraus in ein anderes geht, DAS stellt der jeweilige Beobachter fest und es geht NICHT um die eigene Uhr des jeweiligen Beobachters, sondern darum, welche Zeit er auf der Uhr des jeweils anderen System abliest.
Das war der Grund, warum ich den Link eingestellt habe.
Du scheinst mir ausweichen zu wollen, Henry, denn:
- Es ging durchaus um das Extrem des Photons.
- Dennoch gebe ich Dir recht: Es geht auch darum, wie denn nun genau die Wahrnehmungen von Beobachter (einerseits) und beobachtetem Objekt (andererseits) sich unterscheiden.
- Hierzu aber gilt:
- Der Beobachter kann die Uhr des beobachteten Objekt gar nicht einsehen.
- Die SRT allerdings sagt ihm, wie er deren Zeigerstand herrechnen kann aus dem Zeigerstand seiner eigenen Uhr und der durch ihn beobachteten Geschwindigkeit des Objekts.
- Die entsprechende Regel lautet:
- Eine aus Sicht des Beobachters mit Geschwindigkeit v bewegte Uhr geht – aus seiner Sicht – um den Faktor (1 – v2/c2)–1/2 langsamer als seine eigene.
Mit besten Grüßen,
grtgrt
Beitrag 1997-111
Wer Spezielle Relativitätstheorie (SRT) verstehen will, muss sich klar gemacht haben ...
Wer die SRT verstehen will, sollte wissen:
An Okotombrok, Eugen, Henry, Horst und Stueps:
Euch scheint nicht bewusst zu sein, dass die SRT — anders als die ART —
Und speziell für Horst, sei gesagt, dass das Wort "sehen" hier nicht allzu wörtlich verstanden werden darf:
Es steht für "sehen könnten unter der Voraussetzung, dass jedes Objekt die Fähigkeit hat, beliebig weit absolut genau zu sehen".
In moderner Terminologie kann man das Szenario, in dem die SRT argumentiert, ohne Beschränkung der Allgemeinheit beschreiben wie folgt:
KONSEQUENZ all dessen ist ( jeder überlege sich das auch selbst ):
Erst wer das verstanden hat, hat die SRT w i r k l i c h verstanden.
Beste Grüße,
grtgrt
An Okotombrok, Eugen, Henry, Horst und Stueps:
Euch scheint nicht bewusst zu sein, dass die SRT — anders als die ART —
- gar nicht darüber spricht, wie schnell ein Objekt a l t e r t ,
- sondern n u r darüber, wie schnell andere, zu ihm gleichförmig bewegte Objekte es altern s e h e n.
Und speziell für Horst, sei gesagt, dass das Wort "sehen" hier nicht allzu wörtlich verstanden werden darf:
Es steht für "sehen könnten unter der Voraussetzung, dass jedes Objekt die Fähigkeit hat, beliebig weit absolut genau zu sehen".
In moderner Terminologie kann man das Szenario, in dem die SRT argumentiert, ohne Beschränkung der Allgemeinheit beschreiben wie folgt:
- Betrachtet wird ein 3-dimensionaler Raum, in dem sich Personen (sog. Beobachter) befinden.
- Jeder Beobachter trägt eine Uhr mit sich, und all diese Uhren sind von absolut gleicher Bauart.
- Jeder Beobachter X hat einen PC, dessen Bildschirm stets zwei Uhren zeigt: Die eigene und die eines anderen Beobachters Y.
- Jede Uhr sendet bei jedem ihrer Ticks ein Signal aus, welches all diese Computer empfangen und so die auf ihren Bildschirmen gezeigten Uhrenbilder aktualisieren.
- Der Zeitbegriff eines Beobachters X ist stets der, den das Bild seiner e i g e n e n Uhr ihm erzeugt.
- Zeit (in diesem Sinne) sieht X als eine vierte Dimension des Raumes, in dem er und alle anderen existieren.
- Wo zwei Beobachter sich relativ zueinander bewegen, geschieht dies mit konstanter Geschwindigkeit v < c.
KONSEQUENZ all dessen ist ( jeder überlege sich das auch selbst ):
- Genau dann, wenn zwei Beobachter sich voneinander entfernen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen l a n g s a m e r gehen als seine eigene (der Endlichkeit der Signalgeschwindigkeit wegen).
- Genau dann, wenn zwei Beobachter sich auf einander zu bewegen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen s c h n e l l e r gehen als seine eigene (wieder der Endlichkeit der Signalgeschwindigkeit wegen).
Beste Grüße,
grtgrt
Beitrag 1997-140
Die Geometrie der Raumzeit der SRT ist nicht euklidisch (!)
Was ich noch nicht wusste ...
Da in der Definition der Minkowski-Metrik ein Minus-Zeichen auftritt, ist die Raumzeit – auch die ungekrümmte der SRT – nicht euklidisch (!).
Quelle: Wikipedia
Was ich noch nicht wusste ...
Da in der Definition der Minkowski-Metrik ein Minus-Zeichen auftritt, ist die Raumzeit – auch die ungekrümmte der SRT – nicht euklidisch (!).
Quelle: Wikipedia
Beitrag 786-88
Interessantes zu Gravitationswellen
Interessantes zu Gravitationswellen
Hulse und Taylor erhielten für diese ihre Entdeckung 1993 den Nobelpreis.
Zitat von Maalampi, S 144:
Findet in einer Entfernung von 10.000 Lichtjahren eine Supernova-Explosion statt, so führt die dadurch erzeugte Gravitationswelle dazu, dass die Körpergröße der Menschen für einen Moment um ungefähr den hundertsten Teil eines Atomkerns größer oder kleiner wird.
Der Raum ist voller kleiner Gravitationsschwingungen, ganz so wie er heute voller Radiowellen, Handywellen und anderer Formen elektromagnetischer Strahlung ist.
Zitat von Maalampi, S 147:
Für die [ von der ART vorausgesagte] Existenz von Gravitationswellen gibt es bislang nur eine — indirekte — Bestätigung:
Im Jahr 1974 entdeckten Russell Hulse und Joseph Taylor mit einem Radioteleskop den Doppelpulsar PSR1913 + 16, ein System zweier schnell rotierender Neutronensterne. Sie umkreisen einander mit hoher Geschwindigkeit (alle 8 Std ein Mal). Man stellte fest, dass die Umlaufzeit langsam aber sicher kürzer wird, was zeigt, dass jene Neutronensterne einander in immer kleinerem Abstand umkreisen.
Die ART sagt genau das vorher: Das System verliert ständig Energie, indem es Gravitationswellen in den Raum abstrahlt, weswegen sich die Sterne annähern.
Hulse und Taylor erhielten für diese ihre Entdeckung 1993 den Nobelpreis.
Beitrag 786-80
Zur Geschichte unseres Universums
Hi Real,
auch mich beschäftigt diese Frage, und wenn man VSL-Theorien mal ignoriert (also annimmt, dass die Lichtgeschwindigkeit sich seit dem Urknall nie geändert hat und tatsächlich im gesamten Universum dieselbe ist), so könnte sich der grüne Teil deiner Frage beantworten wie folgt:
Man glaubt heute, dass das Universum sich aufbläht wie ein Hefeteig, in dem sich "Rosinen" finden: Raum-Regionen mit großer Materiedichte, deren Volumen sich NICHT ebenso aufbläht, da hier die Gravitationskraft dem Druck, der überall sonst die Aufblähung des Raumes zur Folge hat, allzu stark entgegenwirkt. Jene Aufblähung hat heute z.B. zur Folge, dass der Abstand zwischen den Rosinen pro Megaparsec (etwa 3.24 Mio. Lichtjahre) jede Sekunde um etwa 74 km wächst.
Die älteste Galaxie, die Astronomen bisher entdeckt zu haben glauben, ist mehr als 13 Mrd. Jahre alt und lebt in einer Rosine G, die deswegen heute von Ort unserer Milchstraße, den ich jetzt mal die Rosine M nenne, gut 45 Mrd. Lichtjahre entfernt ist. Dass das mehr als nur 13 sind, liegt daran, dass der Abstand zwischen G und M ja auch während der Zeit, die das Licht zu uns unterwegs war, ständig größer wurde.
Auf die Zahl 40 kommt man, da man zu wissen glaubt, wie sich die Aufblähgeschwindigkeit entwickelt hat, nachdem das Universum etwa 400 Mio. Jahre alt war.
Wie sie vorher war, kann man wohl gar nicht wissen, da die kosmische Hintergrundstrahlung das älteste Licht ist, welches uns ein klares Bild zeichnen kann. Noch älteres, bei uns ankommendes Licht ist stark gestreut, kann uns also nur Bilder von damals Existierendem zeichnen, die aussehen als hätte man es durch eine Milchglasscheibe photographiert. Das liegt daran, dass sich Materie damals noch nicht zu Atomen gruppiert hatte: Jene sind elektrisch neutral und streuen das Licht deswegen nicht, sich vorher unabhängig voneinander bewegende Materieteilchen aber — Protonen, Elektronen, und was sonst noch — tragen Ladung und haben das Licht deswegen ständig in jede nur denkbare Richtung abgelenkt.
Dass der Urknall — wie man erst kürzlich neu nachgerechnet hat — vor etwa 13.81 Mrd. Jahren stattfand, bedeutet nichts anderes, als dass der Abstand zwischen G und M damals auch nicht größer als nur eine Plancklänge war (bitte beachte: Was ich G und M nenne, sind Raumregionen. Zu sich nicht mehr weiter aufblähenden Rosinen wurden jene Regionen erst später, als sich dort ganz massiv Materie zu verklumpen begann und so jene Galaxie und unsere Milchstraße entstanden).
Dies mal als korrekt angenommen und zudem berücksichtigt, dass die Aufblähgeschwindigkeit des Raumes, wie man weiß, NICHT durch die Lichtgeschwindigkeit begrenzt ist, also unmittelbar nach dem Urknall so gut wie jede Größe gehabt haben kann, ergibt sich:
Gruß, grtgrt
Real in 786-6:Die Frage war kosmologisch gemeint und lautete:
Wie kann man über die Entfernung bzw. das Alter einer Lichtquelle Rückschlüsse auf einen Urknall und dessen Raumverhalten machen?
Mir leuchtet dabei nicht ein, wie etwas schon vor 14 Mrd. Jahren Licht aus einer entsprechenden Entfernung aussenden konnte, wo es doch gerade erst in sich entstand und relativ klein war.
Ich zweifle damit die einfache Logik der Urknall-Theorie an oder wo liegt mein Gedankenfehler?
Wäre nett, wenn mir jemand diese Logik begreiflich machen könnte.... Real
Hi Real,
auch mich beschäftigt diese Frage, und wenn man VSL-Theorien mal ignoriert (also annimmt, dass die Lichtgeschwindigkeit sich seit dem Urknall nie geändert hat und tatsächlich im gesamten Universum dieselbe ist), so könnte sich der grüne Teil deiner Frage beantworten wie folgt:
Man glaubt heute, dass das Universum sich aufbläht wie ein Hefeteig, in dem sich "Rosinen" finden: Raum-Regionen mit großer Materiedichte, deren Volumen sich NICHT ebenso aufbläht, da hier die Gravitationskraft dem Druck, der überall sonst die Aufblähung des Raumes zur Folge hat, allzu stark entgegenwirkt. Jene Aufblähung hat heute z.B. zur Folge, dass der Abstand zwischen den Rosinen pro Megaparsec (etwa 3.24 Mio. Lichtjahre) jede Sekunde um etwa 74 km wächst.
Die älteste Galaxie, die Astronomen bisher entdeckt zu haben glauben, ist mehr als 13 Mrd. Jahre alt und lebt in einer Rosine G, die deswegen heute von Ort unserer Milchstraße, den ich jetzt mal die Rosine M nenne, gut 45 Mrd. Lichtjahre entfernt ist. Dass das mehr als nur 13 sind, liegt daran, dass der Abstand zwischen G und M ja auch während der Zeit, die das Licht zu uns unterwegs war, ständig größer wurde.
Auf die Zahl 40 kommt man, da man zu wissen glaubt, wie sich die Aufblähgeschwindigkeit entwickelt hat, nachdem das Universum etwa 400 Mio. Jahre alt war.
Wie sie vorher war, kann man wohl gar nicht wissen, da die kosmische Hintergrundstrahlung das älteste Licht ist, welches uns ein klares Bild zeichnen kann. Noch älteres, bei uns ankommendes Licht ist stark gestreut, kann uns also nur Bilder von damals Existierendem zeichnen, die aussehen als hätte man es durch eine Milchglasscheibe photographiert. Das liegt daran, dass sich Materie damals noch nicht zu Atomen gruppiert hatte: Jene sind elektrisch neutral und streuen das Licht deswegen nicht, sich vorher unabhängig voneinander bewegende Materieteilchen aber — Protonen, Elektronen, und was sonst noch — tragen Ladung und haben das Licht deswegen ständig in jede nur denkbare Richtung abgelenkt.
Dass der Urknall — wie man erst kürzlich neu nachgerechnet hat — vor etwa 13.81 Mrd. Jahren stattfand, bedeutet nichts anderes, als dass der Abstand zwischen G und M damals auch nicht größer als nur eine Plancklänge war (bitte beachte: Was ich G und M nenne, sind Raumregionen. Zu sich nicht mehr weiter aufblähenden Rosinen wurden jene Regionen erst später, als sich dort ganz massiv Materie zu verklumpen begann und so jene Galaxie und unsere Milchstraße entstanden).
Dies mal als korrekt angenommen und zudem berücksichtigt, dass die Aufblähgeschwindigkeit des Raumes, wie man weiß, NICHT durch die Lichtgeschwindigkeit begrenzt ist, also unmittelbar nach dem Urknall so gut wie jede Größe gehabt haben kann, ergibt sich:
- Deine Annahme "wo es [= jene Galaxie] doch gerade erst in sich entstand und relativ klein war" muss als falsch bezeichnet werden
- und über das gesamte Geschehen während der Kindheit unseres Universums (sprich: als es noch keine 400 Mio Jahre alt war) können selbst Physiker und Kosmologen bislang nur spekulieren.
Gruß, grtgrt
Beitrag 786-82
Wie relativ ist das Alter unseres Universums?
Ja Harti, das ist wohl so.
BEGRÜNDUNG: Da es keinen absoluten (sprich: ortsunabhängigen) Zeitbegriff gibt, können wir nur darüber sprechen, wie alt das Universum aus unserer Sicht heraus sein kann.
Meines Wissens nach aber hat bisher aber auch niemand behauptet, dass das Alter des Universums aus Sicht sämtlicher Beobachter gleich sei.
Andererseits aber müsste genau das Folge des kosmologischen Prinzips sein (welches ja postuliert, dass das Universum homogen und isoptrop ist, sich aus Sich aller Beobachter also qualitativ gleich darstellt).
Gruß, grtgrt
PS: Es scheint mir richtig, zu sagen: Ja, grundsätzlich ist all unsere Wahrnehmung relativ (sprich: abhängig von dem Ort im Universum, an dem wir uns befinden). Über all diese Orte hinweg muss sich aber — des kosmologischen Prinzips wegen — immer dieselbe Sicht auf Entstehung und die Qualität der Entwicklung des Universums seit dem Urknall ergeben.
Wahrscheinlich liegt das daran, dass der Urknall ja nicht an e i n e m Ort stattfand, sondern dass
wirklich j e d e r Ort im Universum Teil des Ortes ist, an dem der Urknall stattfand und immer noch stattfindet.
Harti in 786-81:Hallo Grtgrt,
über den Umstand, dass das Universum keinen vom Beobachter unabhängigen Mittelpunkt hat und in der Folge auch kein Rand bestimmt werden kann, ist man sich wissenschaftlich überwiegend einig, oder ? Das bedeutet, Absolutheitsvorstellungen räumlicher Art sind wissenschaftlich obsolet.
Muss man dann nicht auch annehmen, dass Überlegungen zu einem zeitlichen Anfang und Ende des Universums in einem absoluten Sinn nicht wissenschaftlich sind?
Ja Harti, das ist wohl so.
BEGRÜNDUNG: Da es keinen absoluten (sprich: ortsunabhängigen) Zeitbegriff gibt, können wir nur darüber sprechen, wie alt das Universum aus unserer Sicht heraus sein kann.
Meines Wissens nach aber hat bisher aber auch niemand behauptet, dass das Alter des Universums aus Sicht sämtlicher Beobachter gleich sei.
Andererseits aber müsste genau das Folge des kosmologischen Prinzips sein (welches ja postuliert, dass das Universum homogen und isoptrop ist, sich aus Sich aller Beobachter also qualitativ gleich darstellt).
Gruß, grtgrt
PS: Es scheint mir richtig, zu sagen: Ja, grundsätzlich ist all unsere Wahrnehmung relativ (sprich: abhängig von dem Ort im Universum, an dem wir uns befinden). Über all diese Orte hinweg muss sich aber — des kosmologischen Prinzips wegen — immer dieselbe Sicht auf Entstehung und die Qualität der Entwicklung des Universums seit dem Urknall ergeben.
Wahrscheinlich liegt das daran, dass der Urknall ja nicht an e i n e m Ort stattfand, sondern dass
Beitrag 786-87
Gravitationswellen aus dem eben geborenen Universum
Eine Möglichkeit, die Geburt des Universums doch noch zu beobachten
Durch Beobachtung Wissen darüber zu sammeln, was in unserem Universum vor sich ging noch b e v o r es etwa 400 Mio Jahre alt war, scheint möglich über die Beobachtung von Gravitationswellen (die registrierbar zu machen nun in greifbare Nähe rückt):
Der Herausforderung, eine Gravitationsantenne zu bauen, die hinreichend sensibel sein wird, solche Wellen noch zu entdecken, stellt sich ein durch NASA und ESA gemeinsam verantwortetes Projekt LISA (Laser Interferometer Space Antenna), welches ab 2020 Messungen von ganz unglaublicher Genauigkeit ermöglichen wird:
Solche Präzision ist schier unglaublich, wenn man berücksichtigt, wie weit die Satelliten voneinander entfernt sind. Ein Critical Design Review in 2010 aber scheint bestätigt zu haben, dass diese Genauigkeit tatsächlich erreichbar sein wird.
Nebenbei: LISA reagiert empfindlich auf langsame Schwingungen (auf solche, bei denen die Dauer einer Schwingung zwischen 10 und 10.000 sec liegt). Solche Raumwellen werden durch die Bewegung großer Himmelskörper erzeugt, z.B. durch superschwere Schwarze Löcher.
Mir persönlich stellt sich die Frage, wie solche Gravitationswellen schon im ganz jungen Universum entstanden sein können: Energie hatte sich zu jener Zeit ja noch nicht mal zu Atomen verklumpt (!).
PS: Wie ich eben lese, sah sich die NASA schon 2011 gezwungen, einer Budgetkürzung wegen aus dem Projekt LISA auszusteigen. Es wird nun durch die ESA alleine fortgeführt unter dem Namen eLISA. Der ursprüngliche Terminplan ist so natürlich nicht mehr zu halten ... Wurde es im Mai 2012 ganz aufgegeben?
Durch Beobachtung Wissen darüber zu sammeln, was in unserem Universum vor sich ging noch b e v o r es etwa 400 Mio Jahre alt war, scheint möglich über die Beobachtung von Gravitationswellen (die registrierbar zu machen nun in greifbare Nähe rückt):
Zitat von Maalampi, S 147 (2006):
Einige Urknallmodelle sagen messbare Gravitationswellen voraus, die unmittelbar nach dem Ende der sog. Planckzeit entstanden sind, also 10-45 sec nach dem Beginn des Urknalls.
Der Herausforderung, eine Gravitationsantenne zu bauen, die hinreichend sensibel sein wird, solche Wellen noch zu entdecken, stellt sich ein durch NASA und ESA gemeinsam verantwortetes Projekt LISA (Laser Interferometer Space Antenna), welches ab 2020 Messungen von ganz unglaublicher Genauigkeit ermöglichen wird:
Zitat von Maalampi, S 144 (2006):
Die Messung erfolgt im Weltall durch 3 Satelliten, die in der Formation eines gleichseitigen Dreiecks fliegen und jeweils 5 Mio Kilometer voneinander entfernt sind.
Mit Hilfe von Laserstrahlen werden in diesen Satelliten die Abstände zwischen den Testkörpern gemessen.
Bewegen sich die Satelliten in der Größenordnung von nur einer Haaresbreite — tatsächlich reicht auch der millionste Teil einer Haaresbreite — näher aufeinander zu, so entdeckt das Interferometer diese Bewegung.
Solche Präzision ist schier unglaublich, wenn man berücksichtigt, wie weit die Satelliten voneinander entfernt sind. Ein Critical Design Review in 2010 aber scheint bestätigt zu haben, dass diese Genauigkeit tatsächlich erreichbar sein wird.
Nebenbei: LISA reagiert empfindlich auf langsame Schwingungen (auf solche, bei denen die Dauer einer Schwingung zwischen 10 und 10.000 sec liegt). Solche Raumwellen werden durch die Bewegung großer Himmelskörper erzeugt, z.B. durch superschwere Schwarze Löcher.
Mir persönlich stellt sich die Frage, wie solche Gravitationswellen schon im ganz jungen Universum entstanden sein können: Energie hatte sich zu jener Zeit ja noch nicht mal zu Atomen verklumpt (!).
PS: Wie ich eben lese, sah sich die NASA schon 2011 gezwungen, einer Budgetkürzung wegen aus dem Projekt LISA auszusteigen. Es wird nun durch die ESA alleine fortgeführt unter dem Namen eLISA. Der ursprüngliche Terminplan ist so natürlich nicht mehr zu halten ... Wurde es im Mai 2012 ganz aufgegeben?
Beitrag 2065-1
Zur Relativität kosmischer Abstände (in zeitlicher und örtlicher Hinsicht)
Warum Alter und Größe kosmischer Objekte beobachterabhängig sein müssen
In Jukka Maalampi: Die Weltlinie – Einstein und die moderne Physik findet sich in Abschnitt 5.6 ein interessanter Vergleich:
Das Beispiel finde ich interessant, denn wenn wir davon ausgehen, dass unser Universum unendlich groß, homogen und isotrop sowie in ständiger Ausdehnung begriffen ist, muss es darin Materie geben, die sich von uns mit jeder nur denkbaren Geschwindigkeit entfernt, insbesondere mit fast Lichtgeschwindigkeit.
Würde das dann aber nicht bedeuten, dass es z.B. Materie gibt, aus deren Sicht der Durchmesser unserer Milchstraße kleiner als 1 Meter und ihr Alter weit größer als 20 Mrd. Jahre ist?
Schlimmer noch: Wie können wir bei solch unvermeidbarer Relativität denn überhaupt noch davon sprechen, dass unser Universum ein bestimmtes Alter habe? Müsste dann nicht vielmehr das durch uns beobachtbare Alter durch uns beobachtbarer Galaxien umso größer sein, je weiter sie von uns entfernt sind (bzw. je schneller sie sich relativ zu uns bewegen)?
Anders gefragt:
Ist – so gesehen – der Begriff » Alter des Universums « denn überhaupt wohldefinierbar?
In Jukka Maalampi: Die Weltlinie – Einstein und die moderne Physik findet sich in Abschnitt 5.6 ein interessanter Vergleich:
Zitat von Maalampi (nicht wörtlich):
Einsteins Annahme, dass die Lichtgeschwindigkeit konstant ist, mag unschuldig aussehen, hat aber dramatische Folgen:
Wenn ich mich z.B. dadurch beschreibe, dass ich 182 cm groß und 57 Jahre alt bin, hat diese Beschreibung keine absolute Bedeutung, denn:
- Aliens, deren Raumschiff unser Sonnensystem mit 80% Lichtgeschwindigkeit durchquert, würden sehen, dass ich nur etwa 100 cm groß und 83 Jahre alt bin.
- Würden sie gar mit Lichtgeschwindigkeit reisen, sähen sie mich als unendlich klein und unendlich alt.
Das Beispiel finde ich interessant, denn wenn wir davon ausgehen, dass unser Universum unendlich groß, homogen und isotrop sowie in ständiger Ausdehnung begriffen ist, muss es darin Materie geben, die sich von uns mit jeder nur denkbaren Geschwindigkeit entfernt, insbesondere mit fast Lichtgeschwindigkeit.
Würde das dann aber nicht bedeuten, dass es z.B. Materie gibt, aus deren Sicht der Durchmesser unserer Milchstraße kleiner als 1 Meter und ihr Alter weit größer als 20 Mrd. Jahre ist?
Schlimmer noch: Wie können wir bei solch unvermeidbarer Relativität denn überhaupt noch davon sprechen, dass unser Universum ein bestimmtes Alter habe? Müsste dann nicht vielmehr das durch uns beobachtbare Alter durch uns beobachtbarer Galaxien umso größer sein, je weiter sie von uns entfernt sind (bzw. je schneller sie sich relativ zu uns bewegen)?
Anders gefragt:
Beitrag 2065-2
Lichthorizont und Zeithorizont
Lichthorizont und Zeithorizont
Mal angenommen, wir können unserem Universum tatsächlich ein wohldefiniertes Alter zuordnen (was dann derzeit bei 13.81 Mrd. Jahren sieht, was nach meiner Argumentation in 2065-1 aber vielleicht doch mit einem grundsätzlichen Fragezeichen versehen sein müsste).
Sollte unser Universum unendlich groß sein, gibt es dann zwei gedachte, unterschiedlich große Kugeloberflächen um uns herum, die äußerst interessant sind:
Ich würde mich freuen, wenn jemand versuchen wollte, in dieser Argumentation Fehler zu entdecken.
Sie setzt nur voraus, dass auf der Geodäte, die uns mit irgendeinem Ort im Universum verbindet — auf dem Weg also, den das Licht nimmt —, für zueinander gleichförmig bewegte Beobachter alle Voraussetzungen der SRT gegeben sind.
Gebhard Greiter (grtgrt)
Mal angenommen, wir können unserem Universum tatsächlich ein wohldefiniertes Alter zuordnen (was dann derzeit bei 13.81 Mrd. Jahren sieht, was nach meiner Argumentation in 2065-1 aber vielleicht doch mit einem grundsätzlichen Fragezeichen versehen sein müsste).
Sollte unser Universum unendlich groß sein, gibt es dann zwei gedachte, unterschiedlich große Kugeloberflächen um uns herum, die äußerst interessant sind:
- Die eine nenne ich unseren Lichthorizont — er grenzt den uns im Prinzip beobachtbaren Teil des Universums ab von dem, der uns nicht einsehbar sein kann in dem Sinne, das uns von dort kein Licht erreichen kann, da es, uns zu erreichen, länger unterwegs sein müsste als das Alter unseres Universums ihm gestattet.
- Die andere nenne ich unseren Zeithorizont — er grenzt den Teil unseres Universums, den wir zeitlich einordnen können (genauer: in dem unser Zeitbegriff überhaupt anwendbar ist) ab vom unendlich großen Rest des Universums. Die entsprechende Kugel hat endlichen, derzeit mit Lichtgeschwindigkeit wachsenden Durchmesser, und doch hat sie — in zeitlicher Hinsicht — unendlich großen Durchmesser (da alles, was kurz vor diesem Horizont liegt, aus unserer Sicht fast unendlich großes Alter hat).
- Würde unser Universum irgendwann mal statt zu expandieren schrumpfen, würde der Radius des Zeithorizontes mit Lichtgeschwindigkeit kleiner werden, jene Kugel in Sinne unserer Zeit aber dennoch weiter unendlich großen Durchmesser haben.
- Ein Schrumpfen ebenso wie ein Expandieren unserer Raumzeit modifiziert von uns wahrgenommene zeitliche Abstände: Sie schrumpfen bzw. wachsen im selben Umfang, in dem unser Universum schrumpft oder sich aufbläht.
Ich würde mich freuen, wenn jemand versuchen wollte, in dieser Argumentation Fehler zu entdecken.
Sie setzt nur voraus, dass auf der Geodäte, die uns mit irgendeinem Ort im Universum verbindet — auf dem Weg also, den das Licht nimmt —, für zueinander gleichförmig bewegte Beobachter alle Voraussetzungen der SRT gegeben sind.
Gebhard Greiter (grtgrt)
Beitrag 2065-4
-
Hallo Quante,
die meisten Nichtphysiker stellen sich das wohl genau so vor.
Physiker und Kosmologen aber sind inzwischen wirklich überzeugt davon — und verfügen über zahlreiche Hinweise darauf —, dass der Raum n i c h t unabhängig von seinem Inhalt entstand, sondern dass er stattdessen ein Aspekt eben dieses Inhaltes ist.
Raum existiert nur dort, wo auch Energie ist (und sei es nur sog. Vakuumenergie).
Der allgegenwärtigen Quantenfluktuation wegen müssen wir ihn als etwas Lebendiges begreifen.
Mathematiker — und deswegen auch Physiker und Kosmologen — können sich sehr wohl einen Raum vorstellen, der keine Grenzen hat, aber doch nur von endlichem Durchmesser ist (in dem Sinne, dass Wege durch den Raum — genauer: Geodäten im Sinne der ART etwa — nicht beliebig lang sein können ohne am selben Punkt mehrfach vobeizukommen).
Tatsache ist:
Nach aktueller Lehrmeinung ist der Raum grenzenlos. Ob er endliche Ausdehnung hat, ist eine noch offene Frage.
Er bläht sich derzeit auf wie ein Hefeteig, was aber nicht bedeuten muss, dass er endlich ist.
Hätten der Raum und seine Dimensionen schon vor dem Inhalt des Universums bestanden (d.h. schon bevor es irgend etwas, Energie etwa, darin gab), könnte der Ur-
knall wirklich nur wie eine — von einer ganz bestimmten Stelle ausgehende — Explosion gewirkt haben. Diese Stelle müsste dann in einer bestimmten Richtung von uns angesiedelt sein. Was Astronomen aber wirklich beobachten, spricht dafür, dass wir uns dann an genau dieser Stelle — im Zentrum jener Explosion — befinden müssten. Wie sonst könnten sich dann nämlich alle fernen Galaxien radial von uns und gleichzeitig vom Explosionszentrum weg bewegen?
Kurz: All unsere Beobachtungen deuten auf überall im Großen gleichmäßige Aufblähung des Raumes hin. Damit ist der gesamte Raum identisch mit dem Punkt, der den Urknall hervorgebracht hat, und jener Urknall kann erst dann als beendet gelten, wenn das Universum aufgehört hat, sich weiter zu vergrößern und zu gestalten.
Gruß, grtgrt
Quante in 2065-3:
Das unsrige Universum, so wie wir es gegenwärtig in seinen Grenzen grade noch so erkennen können, mag ein Alter von ungefähr 14-15 Mrd. Jahre haben, denn in seiner räumlichen Ausdehnung nimmt es ein Volumen ein, für die das Licht 14 Mrd. Jahre benötigte um es zu "durchlaufen", zurückzulegen.
Der Raum, da gegen (bewußt nicht "dagegen" geschrieben), hat für mich eine Ausdehnung die ins absolut Unendliche geht. Der Raum kann und sollte daher selbst keine Begrenzung für sich aufweisen.
Das bedeutet unser Universum kann in etwa ein Alter von 14-15 Mrd Jahre haben, der Raum da gegen, ist alterslos, alterungslos, es hat ihn immer gegeben und wird es immer geben, eine Altersangabe macht keinen Sinn, da er in seiner Ausdehnung unendlich.
Hallo Quante,
die meisten Nichtphysiker stellen sich das wohl genau so vor.
Physiker und Kosmologen aber sind inzwischen wirklich überzeugt davon — und verfügen über zahlreiche Hinweise darauf —, dass der Raum n i c h t unabhängig von seinem Inhalt entstand, sondern dass er stattdessen ein Aspekt eben dieses Inhaltes ist.
Raum existiert nur dort, wo auch Energie ist (und sei es nur sog. Vakuumenergie).
Der allgegenwärtigen Quantenfluktuation wegen müssen wir ihn als etwas Lebendiges begreifen.
Mathematiker — und deswegen auch Physiker und Kosmologen — können sich sehr wohl einen Raum vorstellen, der keine Grenzen hat, aber doch nur von endlichem Durchmesser ist (in dem Sinne, dass Wege durch den Raum — genauer: Geodäten im Sinne der ART etwa — nicht beliebig lang sein können ohne am selben Punkt mehrfach vobeizukommen).
Tatsache ist:
Nach aktueller Lehrmeinung ist der Raum grenzenlos. Ob er endliche Ausdehnung hat, ist eine noch offene Frage.
Er bläht sich derzeit auf wie ein Hefeteig, was aber nicht bedeuten muss, dass er endlich ist.
Hätten der Raum und seine Dimensionen schon vor dem Inhalt des Universums bestanden (d.h. schon bevor es irgend etwas, Energie etwa, darin gab), könnte der Ur-
knall wirklich nur wie eine — von einer ganz bestimmten Stelle ausgehende — Explosion gewirkt haben. Diese Stelle müsste dann in einer bestimmten Richtung von uns angesiedelt sein. Was Astronomen aber wirklich beobachten, spricht dafür, dass wir uns dann an genau dieser Stelle — im Zentrum jener Explosion — befinden müssten. Wie sonst könnten sich dann nämlich alle fernen Galaxien radial von uns und gleichzeitig vom Explosionszentrum weg bewegen?
Kurz: All unsere Beobachtungen deuten auf überall im Großen gleichmäßige Aufblähung des Raumes hin. Damit ist der gesamte Raum identisch mit dem Punkt, der den Urknall hervorgebracht hat, und jener Urknall kann erst dann als beendet gelten, wenn das Universum aufgehört hat, sich weiter zu vergrößern und zu gestalten.
Gruß, grtgrt
Beitrag 2065-6
-
Ja, Quante, Du hast recht,
und deswegen halte ich b e i d e Aussagen für richtig (meine grüne und deine rote).
Es sind zwei Sichten auf etwas (unsere Welt), in dem sich Raum und Inhalt des Raumes einfach nicht voneinander trennen lassen.
Lassen wir das Multiversum mal außen vor (es ist ja bislang nur Spekulation, und selbst wenn es mehrere Universen geben sollte, bedeutet das noch lange nicht, dass sie in etwas eingebettet sein müssen, was die Bezeichnung "Raum" rechtfertigen würde).
Was ich den Lichthorizont nenne, ist eine (beobachterspezifisch definierte, nur gedanklich existierende) Kugeloberfläche,
Der gesamte Raum wird komplett abgedeckt durch eine Vereinigung solcher Kugeln, denn einen Beobachter kann man sich ja überall positioniert vorstellen.
Sterne und Galaxien finden sich also innerhalb u n d außerhalb so eines Lichthorizontes — wobei das Licht der sich außerhalb befindenden den Beobachter aber nicht erreichen kann, so dass er jene Himmelskörper niemals zu Gesicht bekommt.
Deine Annahme also, ich hätte direkt oder indirekt behauptet, der Raum sei ausgedehnter als das Universum, ist nur ein Missverständnis deinerseits (und würde ja auch dem allseits anerkannten kosmologischen Prinzip widersprechen).
Was nun den Raum als "Aspekt" betrifft, erinnere ich an Brian Greenes Aussage auf Seite 485 seines Buches The Fabric of the Cosmos :
Diese seine Aussage bedeutet:
Was wir als "Raum" — ohne seinen Inhalt — sehen, ist vor allem eine mathematische Hilfskonstruktion, die uns erlaubt, unser M o d e l l der Raumzeit verständlich zu formulieren. Da nun aber jedes Modell nur bestimmte Aspekte des zu modellierenden Gegenstandes mehr oder weniger gut durch Analogien beschreibt, ist kein Modell konkurrenzlos oder allzu wörtlich zu nehmen. Sogar was die Zahl der Dimensionen unser Welt betrifft, sind sie sich keineswegs immer einig und können dennoch sehr gute Modelle sein (!).
Treffendes Beispiel hierfür sind die ART und die Quantentheorie: Beide sind gut erprobt und extrem nützlich, machen aber doch auch Aussagen, die — wenn man eine bestimmte Größenskala zugrundelegt — von entsprechenden Aussagen der jeweils anderen deutlich abweichen.
Kein Wunder: Denn jede der beiden entstand ausgehend von Beobachtungen, die sich wirklich deutlich machen nur für besonders große bzw. besonders kleine Objekte. Somit war fast zu erwarten, dass jedes der beiden Modelle irgendwo hinkt.
Quante in 2065-5:
Von daher läßt sich deine Behauptung: » Raum existiert nur dort, wo auch Energie ist (und sei es nur sog. Vakuumenergie) « ganz einfach ins gegenteilige Postulat umkehren: » Energie existiert nur dort, wo auch Raum ist «. Denn die Existenz von Energie ohne jeglichen sie umgebenden Raum erscheint mir zumindest hinterfragungswürdig.
Ja, Quante, Du hast recht,
und deswegen halte ich b e i d e Aussagen für richtig (meine grüne und deine rote).
Es sind zwei Sichten auf etwas (unsere Welt), in dem sich Raum und Inhalt des Raumes einfach nicht voneinander trennen lassen.
Quante in 2065-5:
Du schreibst: "Physiker und Kosmologen ... sind ... überzeugt, dass der Raum...ein Aspekt eben dieses Inhaltes ist."
Wie kann etwas (der Raum), der in seiner Ausdehnung wesentlich größer und umfangreicher ist (sein soll), Aspekt eines kleinerem, dem Universum, sein?
... für mich ist das Universum lediglich eher noch ein "Aspekt" des Raumes. Wobei ich mich mit der Sichtweise anfreunden kann, daß es sehr, sehr viele verschiedene Universen geben kann.
Lassen wir das Multiversum mal außen vor (es ist ja bislang nur Spekulation, und selbst wenn es mehrere Universen geben sollte, bedeutet das noch lange nicht, dass sie in etwas eingebettet sein müssen, was die Bezeichnung "Raum" rechtfertigen würde).
Was ich den Lichthorizont nenne, ist eine (beobachterspezifisch definierte, nur gedanklich existierende) Kugeloberfläche,
- deren Radius sich aus dem Alter des Universums und seiner bisherigen Expansionsrate ergibt
- und deren Mittelpunkt der Ort ist, an dem sich der Beobachter befindet.
Der gesamte Raum wird komplett abgedeckt durch eine Vereinigung solcher Kugeln, denn einen Beobachter kann man sich ja überall positioniert vorstellen.
Sterne und Galaxien finden sich also innerhalb u n d außerhalb so eines Lichthorizontes — wobei das Licht der sich außerhalb befindenden den Beobachter aber nicht erreichen kann, so dass er jene Himmelskörper niemals zu Gesicht bekommt.
Deine Annahme also, ich hätte direkt oder indirekt behauptet, der Raum sei ausgedehnter als das Universum, ist nur ein Missverständnis deinerseits (und würde ja auch dem allseits anerkannten kosmologischen Prinzip widersprechen).
Was nun den Raum als "Aspekt" betrifft, erinnere ich an Brian Greenes Aussage auf Seite 485 seines Buches The Fabric of the Cosmos :
Zitat von Greene:
More and more, these clues point toward the conclusion that the form of spacetime is an adorning detail that varies from one formulation of a physical theory to the next, rather than being a fundamental element of reality. Much as the number of letters, syllables, and vowels in the word cat differ from those in gato, its Spanish translation, the form of spacetime — its shape, its size, and even the number of its dimensions — also changes in translation.
Diese seine Aussage bedeutet:
Was wir als "Raum" — ohne seinen Inhalt — sehen, ist vor allem eine mathematische Hilfskonstruktion, die uns erlaubt, unser M o d e l l der Raumzeit verständlich zu formulieren. Da nun aber jedes Modell nur bestimmte Aspekte des zu modellierenden Gegenstandes mehr oder weniger gut durch Analogien beschreibt, ist kein Modell konkurrenzlos oder allzu wörtlich zu nehmen. Sogar was die Zahl der Dimensionen unser Welt betrifft, sind sie sich keineswegs immer einig und können dennoch sehr gute Modelle sein (!).
Treffendes Beispiel hierfür sind die ART und die Quantentheorie: Beide sind gut erprobt und extrem nützlich, machen aber doch auch Aussagen, die — wenn man eine bestimmte Größenskala zugrundelegt — von entsprechenden Aussagen der jeweils anderen deutlich abweichen.
Kein Wunder: Denn jede der beiden entstand ausgehend von Beobachtungen, die sich wirklich deutlich machen nur für besonders große bzw. besonders kleine Objekte. Somit war fast zu erwarten, dass jedes der beiden Modelle irgendwo hinkt.
Beitrag 2102-30
Lichthorizont und Ereignishorizont (= Zeithorizont)
Einige Bemerkungen zum "kosmischen Ereignishorizont", denn die Sache liegt nicht ganz so einfach. Man muss genau auseinander halten, WELCHEN Horizont man meint, nämlich den "Beobachtungshorizont" oder den "Ereignishorizont" (ich muss zugeben, dass ich daran auch nicht immer denke, weil ich mich zu selten damit beschäftige).
Der Beobachtungshorizont begrenzt die Sicht eines Beobachters in die Ferne des Alls insofern, als er die Grenze für den Bereich darstellt, über den wir BIS ZU EINEM BESTIMMTEN ZEITPUNKT noch keine Informationen erhalten haben. Dieser Horizont - diese Grenze - erweitert sich mit LG, wird also ständig größer. Wir erhalten ständig mehr Informationen aus Bereichen des Kosmos, die so Schritt für Schritt zugänglich werden. Ist das irgendwie ein Widerspruch zu Expansion des Kosmos selbst? Nein, denn was wir sehen, IST NICHT DIE GESAMTE AUSDEHNUNG DES KOSMOS. Er Beobachtungshorizont dehnt sich in einen BEREITS VORHANDENEN RAUM hinein aus. Der Bereich, den wir auf diese Weise für uns werden in Zukunft erschließen können (rein theoretisch, versteht sich), beträgt etwa achtundvierzig Milliarden Lichtjahre.
Der Ereignishorizont begrenzt den Bereich, hinter den wir niemals werden blicken können, er wird definiert als die Grenze, hinter der sich der Raum mit größer c ausdehnt. DIESER Raumbereich wird nach Schätzungen als zwischen dreißig und einhundert Größenordnungen größer vermutet, als die erwähnten achtundvierzig Milliarden Lichtjahre (wenn eine angenommenen Inflationsphase des Kosmos in den ersten Momenten korrekt ist).
Der Beobachtungshorizont bestimmt die Grenze, innerhalb derer es für Ereignisse kausale Zusammenhänge geben kann, der Ereignishorizont die Grenze, hinter der die Ereignisse keinen kausalen Zusammenhang haben können, weil nichts die Grenze der Lichtgeschwindigkeit ÜBERSCHREITEN kann, was nicht ausschließt, dass es JENSEITS dieser Geschwindigkeit ein "Irgendwas" gibt. Ein irgendwas, wohlgemerkt, das NICHT mit dem sich mit Überlichtgeschwindigkeit ausdehnenden Raum identisch ist, sondern sich auf die Möglichkeit von Bewegung INNERHALB des Raumes bezieht.
Für die Expansion des Raumes - oder besser der Raumzeit - spricht man übrigens nicht von "Geschwindigkeit", sondern von "Expansionsrate", es ist keine Bewegung innerhalb des Raumes, und so gesehen nicht eigentlich eine Geschwindigkeit, womit es auch zu keinen Widersprüchen zur Behauptung kommt, der Raum könne sich mit "Überlichtgeschwindigkeit" ausdehnen. Es macht auch wenig Sinn, von einer Bewegung des Raumes zu sprechen, denn diese "Bewegung" ist NICHT von einem Beobachter abhängig -oder anders - jeder Beobachter beobachtet das Selbe, was ja im Widerspruch zur "Relativität" der Bewegung steht.
Kein allzu leichtes Thema, verbessert mich, wo nötig!�
Der Beobachtungshorizont begrenzt die Sicht eines Beobachters in die Ferne des Alls insofern, als er die Grenze für den Bereich darstellt, über den wir BIS ZU EINEM BESTIMMTEN ZEITPUNKT noch keine Informationen erhalten haben. Dieser Horizont - diese Grenze - erweitert sich mit LG, wird also ständig größer. Wir erhalten ständig mehr Informationen aus Bereichen des Kosmos, die so Schritt für Schritt zugänglich werden. Ist das irgendwie ein Widerspruch zu Expansion des Kosmos selbst? Nein, denn was wir sehen, IST NICHT DIE GESAMTE AUSDEHNUNG DES KOSMOS. Er Beobachtungshorizont dehnt sich in einen BEREITS VORHANDENEN RAUM hinein aus. Der Bereich, den wir auf diese Weise für uns werden in Zukunft erschließen können (rein theoretisch, versteht sich), beträgt etwa achtundvierzig Milliarden Lichtjahre.
Der Ereignishorizont begrenzt den Bereich, hinter den wir niemals werden blicken können, er wird definiert als die Grenze, hinter der sich der Raum mit größer c ausdehnt. DIESER Raumbereich wird nach Schätzungen als zwischen dreißig und einhundert Größenordnungen größer vermutet, als die erwähnten achtundvierzig Milliarden Lichtjahre (wenn eine angenommenen Inflationsphase des Kosmos in den ersten Momenten korrekt ist).
Der Beobachtungshorizont bestimmt die Grenze, innerhalb derer es für Ereignisse kausale Zusammenhänge geben kann, der Ereignishorizont die Grenze, hinter der die Ereignisse keinen kausalen Zusammenhang haben können, weil nichts die Grenze der Lichtgeschwindigkeit ÜBERSCHREITEN kann, was nicht ausschließt, dass es JENSEITS dieser Geschwindigkeit ein "Irgendwas" gibt. Ein irgendwas, wohlgemerkt, das NICHT mit dem sich mit Überlichtgeschwindigkeit ausdehnenden Raum identisch ist, sondern sich auf die Möglichkeit von Bewegung INNERHALB des Raumes bezieht.
Für die Expansion des Raumes - oder besser der Raumzeit - spricht man übrigens nicht von "Geschwindigkeit", sondern von "Expansionsrate", es ist keine Bewegung innerhalb des Raumes, und so gesehen nicht eigentlich eine Geschwindigkeit, womit es auch zu keinen Widersprüchen zur Behauptung kommt, der Raum könne sich mit "Überlichtgeschwindigkeit" ausdehnen. Es macht auch wenig Sinn, von einer Bewegung des Raumes zu sprechen, denn diese "Bewegung" ist NICHT von einem Beobachter abhängig -oder anders - jeder Beobachter beobachtet das Selbe, was ja im Widerspruch zur "Relativität" der Bewegung steht.
Kein allzu leichtes Thema, verbessert mich, wo nötig!�
Beitrag 2102-31
-
Dabei darf man nicht vergessen, daß dieses ankommende Licht abgeschickt wurde, als das Universum noch dichter zusammengezogen war. Wir sehen also sozusagen ein Abbild einer kleinen Briefmarke von Anno dazumal auf einer großen 3D-"Kinoleinwand" von heute.Henry in 2102-30:Der Bereich, den wir auf diese Weise für uns werden in Zukunft erschließen können (rein theoretisch, versteht sich), beträgt etwa achtundvierzig Milliarden Lichtjahre.
Beitrag 2068-7
Unser Zeitbegriff e n d e t am Zeithorizont
Hallo Harti,
was Du da sagst (oder glaubst) ist mit Sicherheit falsch, denn außerhalb unseres Zeithorizonts (der dort liegt, wo Objekte, die Ruhemasse haben, sich aus unserer Sicht nicht mehr langsamer als das Licht bewegen) gibt es den Begriff » Zeit aus unserer Sicht « gar nicht mehr: siehe Beitrag 2065-2.
Insbesondere lassen sich dort die Argumente von SRT und ART n i c h t mehr anwenden.
Gruß, grtgrt
Harti in 2068-6:Hallo C...,
ich habe ja schon mal für die SRT die Ansicht vertreten, ein Überschreiten der Lichtgeschwindigkeit bedeute, dass die Raum- und Zeitkoordinate ihre Bedeutung ändern.
Dies hat zur Folge, dass ein Objekt nach Überschreiten der Lichtgeschwindigkeit sich wieder in Richtung Zeitachse bewegt und damit langsamer wird.
Kann man sich im Rahmen der ART vorstellen, dass am Ereignishorizont Entsprechendes passiert ?
Hallo Harti,
was Du da sagst (oder glaubst) ist mit Sicherheit falsch, denn außerhalb unseres Zeithorizonts (der dort liegt, wo Objekte, die Ruhemasse haben, sich aus unserer Sicht nicht mehr langsamer als das Licht bewegen) gibt es den Begriff » Zeit aus unserer Sicht « gar nicht mehr: siehe Beitrag 2065-2.
Insbesondere lassen sich dort die Argumente von SRT und ART n i c h t mehr anwenden.
Gruß, grtgrt
Beitrag 786-96
Durchmesser des uns heute sichtbaren Universums
Na ja, qualitativ gesehen argumentieren wir ja beide gleich, und zudem ist die Rechnung komplizierter, als Du sie hier skizzierst, denn:
Die von mir genannte Zahl ( 46 Mrd. Lichtjahre = Durchmesser des uns heute sichtbaren Universums ) wurde natürlich nicht von mir errechnet, sondern von MartinB oder von Leuten, denen er in seiner Rolle als Hochschullehrer für Physik traut (siehe auch die letzten Zeilen seines Artikels, wo sich eben diese Zahl findet).
Seine Zahlen werden bestätigt auf Wikipedias Seite The Observable Universe.
Bernhard Kletzenbauer in 786-92:
Doch wie dem auch sei, durch das Summieren der Einzelgeschwindigkeiten erreicht man bei einer Entfernung von ungefähr 14 Mrd. Lichtjahren eine Expansionsgeschwindigkeit von 300000 km/s und mehr. Das bedeutet, daß Erde und Lichtquelle sich schneller als das Licht voneinander entfernen. Aus 40 Mrd. Lj. Entfernung kann noch kein Licht bei uns angekommen sein.
Es ist vielmehr so, daß das Licht der weitest entfernten Galaxie und der Hintergrundstrahlung losgeschickt wurde, als das Universum viel dichter zusammengepresst war (nicht zu einem Punkt!). Nehmen wir mal an, daß der Abstand zum Beispiel damals 1 Megaparsec war. Dann ist das Licht fast 14 Milliarden Jahre gegen die kosmische Expansion angerannt, und erst jetzt bei uns angekommen.
Also, Startentfernung 3 260 000 Lichtjahre, Entfernung bei Ankunft fast 14 000 000 000 Lichtjahre.
Na ja, qualitativ gesehen argumentieren wir ja beide gleich, und zudem ist die Rechnung komplizierter, als Du sie hier skizzierst, denn:
- Die Expansionsgeschwindigkeit hat sich im Laufe der Zeit ja durchaus geändert (und dürfte ganz am Anfang deutlich größer als heute gewesen sein).
- Und die Geschwindigkeit, mit der sich Galaxien von uns entfernen, wird mit zunehmender Entfernung immer größer.
- Damit scheint es mir schon möglich, dass die Quelle des Lichtes, das heute bei uns ankommt, derzeit von uns deutlich weiter entfernt ist als nur 14 Mrd. Lichtjahre: Sie war damals noch innerhalb, ist aber heute weit außerhalb unseres Lichthorizonts.
Die von mir genannte Zahl ( 46 Mrd. Lichtjahre = Durchmesser des uns heute sichtbaren Universums ) wurde natürlich nicht von mir errechnet, sondern von MartinB oder von Leuten, denen er in seiner Rolle als Hochschullehrer für Physik traut (siehe auch die letzten Zeilen seines Artikels, wo sich eben diese Zahl findet).
Seine Zahlen werden bestätigt auf Wikipedias Seite The Observable Universe.
Beitrag 786-105
-
Die 46 Mrd. Lichtjahre sind ganz klar mitbewegte Entfernung.
Es gab da wohl auch unter Fachleuten einige Verwirrung. Daher wohl die Klarstellung im Papier Superluminal Recession Velocities (2001).
Siehe auch Wikipedias Seite The Observable Universe.
Bernhard Kletzenbauer in 786-100:Grtgrt in 786-96:
Die von mir genannte Zahl ( 46 Mrd. Lichtjahre = Durchmesser des uns heute sichtbaren Universums ) wurde natürlich nicht von mir errechnet, sondern von MartinB oder von Leuten, denen er in seiner Rolle als Hochschullehrer für Physik traut (siehe auch die letzten Zeilen seines Artikels, wo sich eben diese Zahl findet).
Ich habe einen Artikel gelesen, in dem von verschiedenen Universum-Horizonten die Rede ist (Leuchtkraftentfernung, mitbewegte Entfernung, Winkeldurchmesserentfernung,...) Es kommt immer darauf an, von welcher Seite man es sieht.
http://scienceblogs.de/astrodicticum-simplex/2012/0...
Die 46 Mrd. Lichtjahre sind ganz klar mitbewegte Entfernung.
Es gab da wohl auch unter Fachleuten einige Verwirrung. Daher wohl die Klarstellung im Papier Superluminal Recession Velocities (2001).
Siehe auch Wikipedias Seite The Observable Universe.
Beitrag 2065-8
Kein Wesen hat unendlich weiten Lebensraum
In Beitrag 2065-7 wurde festgestellt, dass Objekte, deren Zeithorizont zueinander disjunkt ist, sich weder zeitlich noch räumlich in Beziehung zueinander setzen lassen.
Andererseits ist die Raumregion im Inneren des Zeithorizonts immer nur endlich groß — auch dann, wenn das Universum flach und unendlich groß sein sollte.
Beide Tatsachen zusammengenommen zeigen uns:
Selbst wenn unser Universum unendlich groß sein sollte, wohnen wir de facto doch in einem nur endlich großen Universum.
Unser Zeithorizont ist seine äußerste Grenze.
Obgleich sie nur gedanklich existiert und für je zwei Personen an leicht unterschiedlicher Stelle liegt,
wirkt sie wie eine real existierende Barriere, über die wir nicht hinwegkommen.
In letzter Konsequenz bedeutet das, dass jedes im All lebende Wesen sein ganz persönliches, eigenes Universum hat. Je weiter solche Wesen räumlich voneinander getrennt residieren, desto weniger überlappen sich ihre Universen (= maximal großen Lebensräume).
Obgleich diese virtuellen "Universen" sich oft stark überlappen, beginnen sie doch recht schnell, sich auseinander zu entwickeln:
In Beitrag 2065-7 wurde festgestellt, dass Objekte, deren Zeithorizont zueinander disjunkt ist, sich weder zeitlich noch räumlich in Beziehung zueinander setzen lassen.
Andererseits ist die Raumregion im Inneren des Zeithorizonts immer nur endlich groß — auch dann, wenn das Universum flach und unendlich groß sein sollte.
Beide Tatsachen zusammengenommen zeigen uns:
Unser Zeithorizont ist seine äußerste Grenze.
Obgleich sie nur gedanklich existiert und für je zwei Personen an leicht unterschiedlicher Stelle liegt,
wirkt sie wie eine real existierende Barriere, über die wir nicht hinwegkommen.
In letzter Konsequenz bedeutet das, dass jedes im All lebende Wesen sein ganz persönliches, eigenes Universum hat. Je weiter solche Wesen räumlich voneinander getrennt residieren, desto weniger überlappen sich ihre Universen (= maximal großen Lebensräume).
Obgleich diese virtuellen "Universen" sich oft stark überlappen, beginnen sie doch recht schnell, sich auseinander zu entwickeln:
Zitat von Maalampi, S. 84:
Zum Beispiel unterscheiden sich die Entfernungen zwischen Merkur und Sonne — in Abhängigkeit davon, ob die Messungen von der Oberfläche des Merkur oder von der Sonnenoberfläche aus durchgeführt werden — um etwa 100 Kilometer.
Zitat von Maalampi, S. 93:
Und: Auf der Oberfläche der Sonne geht die Zeit im Vergleich zur Erdzeit 64 sec pro Jahr nach, in der Mitte der Sonne sind es ungefär 5 Min. Somit hat sich der Zeitunterschied in der 5 Mrd. Jahre währenden Lebenszeit unseres Sonnensystems auf schon Tausende von Jahren akkumuliert.
Beitrag 2068-22
-
Harti hat recht, denn die Physiker sagen:
Aus Sicht jeden Beobachters, für den Zeit vergeht, legt Licht in jeder Sekunde 299 792 458 m zurück.
Da man die Länge einer Sekunde über den Taktgeber einer geeigneten Atomuhr definiert, ist diese Aussage zudem noch Definition der Längeneinheit Meter (= m).
Horst in 2068-17:Harti im Beitrag 2068-15
Zitat:Während sich das Licht im Raum 300000 km bewegt, bewegt es sich in der Zeit 1 sec.
Hallo Harti
Ich bin der Ansicht, das Licht bewegt sich nicht "in der Zeit", sondern nur im Raum.
Es dauert 1 sec bis es im Raum die Strecke von 300000 km zurückgelegt hat.
Harti hat recht, denn die Physiker sagen:
Beitrag 2068-24
-
Hallo Harti,
die Frage ist, aus Sicht welchen Beobachters sich Licht durch die Zeit bewegt.
Dass Licht sich durch die Zeit bewege, kann nur jemand sagen, dem klar ist, dass das Bild der Lichtquelle, welches jenes Licht uns zeigt, ein Bild aus der Vergangenheit der Lichtquelle ist. Das Licht, die Lichtquelle, und wir haben aber jeder einen anderen Zeitbegriff (!).
Wenn man sagt, etwas bewege sich durch die Zeit, dann meint man den Zeitbegriff, den jenes Etwas hat. Wenn jenes Etwas aber das Licht ist, lässt sich nur feststellen:
Die Projektion seines Geschwindigkeitsvektors auf die Zeit ist Null. Es kennt keine Zeit.
Wenn dein Diagramm auch Geschwindigkeiten größer als c kennt, finde ich daran nichts Besonderes, denn es gibt sie ja: Aufgrund der Expansion des Alls gibt es Galaxien, die sich von uns mit beliebig großer Geschwindigkeit entfernen (jedenfalls dann, wenn das All wirklich homogen, isotrop und unendlich groß sein sollte).
Da alle Argumentation der SRT davon ausgeht, dass nur das Licht es Objekten ermöglicht, einander Information zukommen zu lassen, kann die Welt jedes solchen Objekts nur aus Dingen bestehen, die sich relativ zu ihm mit einer Geschwindigkeit kleiner c bewegen. In jener Welt also ist c die Höchstgeschwindigkeit (da alles, was sich schneller bewegt, dort einfach nicht wahrnehmbar ist).
Gruß, grtgrt
Harti in 2068-15:Während sich das Licht im Raum 300000 km bewegt, bewegt es sich in der Zeit 1 sec.
Es ist auf der Grundlage dieses Diagramms nicht erklärbar, warum die Bewegung eines Objekts mit z.B. 400000 km/sec nicht möglich ist. Die Lichtgeschwindigkeit wird deshalb auf der Grundlage der SRT als Höchstgeschwindigkeit postuliert.
Hallo Harti,
die Frage ist, aus Sicht welchen Beobachters sich Licht durch die Zeit bewegt.
Dass Licht sich durch die Zeit bewege, kann nur jemand sagen, dem klar ist, dass das Bild der Lichtquelle, welches jenes Licht uns zeigt, ein Bild aus der Vergangenheit der Lichtquelle ist. Das Licht, die Lichtquelle, und wir haben aber jeder einen anderen Zeitbegriff (!).
Wenn man sagt, etwas bewege sich durch die Zeit, dann meint man den Zeitbegriff, den jenes Etwas hat. Wenn jenes Etwas aber das Licht ist, lässt sich nur feststellen:
Die Projektion seines Geschwindigkeitsvektors auf die Zeit ist Null. Es kennt keine Zeit.
Wenn dein Diagramm auch Geschwindigkeiten größer als c kennt, finde ich daran nichts Besonderes, denn es gibt sie ja: Aufgrund der Expansion des Alls gibt es Galaxien, die sich von uns mit beliebig großer Geschwindigkeit entfernen (jedenfalls dann, wenn das All wirklich homogen, isotrop und unendlich groß sein sollte).
Da alle Argumentation der SRT davon ausgeht, dass nur das Licht es Objekten ermöglicht, einander Information zukommen zu lassen, kann die Welt jedes solchen Objekts nur aus Dingen bestehen, die sich relativ zu ihm mit einer Geschwindigkeit kleiner c bewegen. In jener Welt also ist c die Höchstgeschwindigkeit (da alles, was sich schneller bewegt, dort einfach nicht wahrnehmbar ist).
Gruß, grtgrt
Beitrag 2068-36
Das Multiversum, in dem wir zu Hause sind (bzw: Raumzeit in dreierlei Bedeutung)
Hallo E...,
man sollte sich darüber klar sein, dass, wer von der Raumzeit spricht, von 3 ganz verschiedenen Dingen sprechen kann. Dies sind
Keine zwei Exemplare vom Typ (3) sind identisch.
Sie sind vergleichbar mit der Sicht eines Menschen, der sich in einem Segelboot weit draußen auf dem Meer herumtreibt in einer Gegend, wo — fern am Horizont — gerade noch einige Inseln zu sehen sind. Der Erdkrümmung wegen wird er i.A. nicht alle sehen, und wenn er sich ihnen nähert, wird die Zahl derer, die er zu sehen bekommt, immer größer. Kurz: Die ihm sichtbare Welt wird anders aussehen je nachdem, an welchem Ort er sich gerade befindet.
Dennoch ist unbestritten: Diese Sichten sind nicht disjunkt zueinander. Sie sind wie Karten, deren Inhalt sich überlappt aber doch nicht identisch ist.
Wenn ich also von mehreren Exemplaren der "Raumzeit" spreche, meine ich damit ortsabhängige Sichten (3) auf unser Universum modelliert über je ein Exemplar (1).
Jede ist zwangsläufig begrenzt durch den Zeithorizont eines Beobachters, der sich am jeweils betrachteten Ort befindet — ist also ein kugelförmiges, begrenztes Universum.
Die Vereinigung aller Universen in diesem Sinne nenne ich das Multiversum, in dem wir zu Hause sind.
Es ist Vereinigung sich überlappender oder nicht überlappender kugelförmiger Teil-Universen, die — wenn beobachterspezifisch definiert — sich zudem noch ständig gegeneinander verschieben, wenn jene Beobachter sich gegeneinander bewegen.
Wir, als ein solcher Beobachter, bewegen uns wenigstens durch die Zeit, und deswegen modifiziert sich unser Universum ständig (und nicht nur deswegen, weil der Raum expandiert).
Gruß, grtgrt
E... in 2068-33:Grtgrt in 2068-31:
... Die Vermischung passiert nicht im Konstrukt "Raumzeit", sondern erst beim Übergang in ein anderes Exemplar davon.
Guten Morgen Grtgrt.
Wieviel Exemplare "Raumzeit" bist Du denn bereit zu bieten, in diesem, unseren Universum?
Mit einem kann ich Dir dienen, aber wo willst Du eine weitere "Raumzeit" herholen in die "übergegangen" werden kann?
Mit gespannten Grüßen.
E....
Hallo E...,
man sollte sich darüber klar sein, dass, wer von der Raumzeit spricht, von 3 ganz verschiedenen Dingen sprechen kann. Dies sind
- (1) die Raumzeit als mathematisches Modell dessen, was wir unser Universum nennen,
- (2) die Raumzeit als das, was unser Universum tatsächlich ist, und
- (3) der jeweils beobachterspezifischen Sicht auf dieses Universum modelliert durch ein Exemplar von Typ (1).
Keine zwei Exemplare vom Typ (3) sind identisch.
Sie sind vergleichbar mit der Sicht eines Menschen, der sich in einem Segelboot weit draußen auf dem Meer herumtreibt in einer Gegend, wo — fern am Horizont — gerade noch einige Inseln zu sehen sind. Der Erdkrümmung wegen wird er i.A. nicht alle sehen, und wenn er sich ihnen nähert, wird die Zahl derer, die er zu sehen bekommt, immer größer. Kurz: Die ihm sichtbare Welt wird anders aussehen je nachdem, an welchem Ort er sich gerade befindet.
Dennoch ist unbestritten: Diese Sichten sind nicht disjunkt zueinander. Sie sind wie Karten, deren Inhalt sich überlappt aber doch nicht identisch ist.
Wenn ich also von mehreren Exemplaren der "Raumzeit" spreche, meine ich damit ortsabhängige Sichten (3) auf unser Universum modelliert über je ein Exemplar (1).
Jede ist zwangsläufig begrenzt durch den Zeithorizont eines Beobachters, der sich am jeweils betrachteten Ort befindet — ist also ein kugelförmiges, begrenztes Universum.
Die Vereinigung aller Universen in diesem Sinne nenne ich das Multiversum, in dem wir zu Hause sind.
Es ist Vereinigung sich überlappender oder nicht überlappender kugelförmiger Teil-Universen, die — wenn beobachterspezifisch definiert — sich zudem noch ständig gegeneinander verschieben, wenn jene Beobachter sich gegeneinander bewegen.
Wir, als ein solcher Beobachter, bewegen uns wenigstens durch die Zeit, und deswegen modifiziert sich unser Universum ständig (und nicht nur deswegen, weil der Raum expandiert).
Gruß, grtgrt
Beitrag 2068-38
-
Hallo Horst,
so sehe ich das im Prinzip auch.
Man muss allerdings berücksichtigen, dass wir dieses gedachte "Bezugssystem" (Koordinatensystem) in der Realität mit einem realen Bezugssystem verbinden müssen. Dies liegt daran, dass wir Bewegung als Gegensatz zu Ruhe auffassen, d.h. Bewegung und Ruhe trennen.
In den Beispielen von Einstein spielt der Bahndamm die Rolle des realen Bezugssystems; dieser Bahndamm (plus Beobachter) wird im vorgestellten Koordinatensystem ruhend vorgestellt.
In den unseren Überlegungen fehlt es häufig an der nötigen Klarheit bezhüglich dieses realen Bezugssystems.
Bei der Angabe, eine Rakete fliegt mit 1000 km/h, bleibt unklar, ob sie diese Geschwindigkeit im Verhältnis zu mir als Beobachter hat, im Verhältnis zur Erde, im Verhältnis zum Sonnensystem oder im Verhältnis zum Universum in seiner Gesamtheit. Ich gehe davon aus, dass ich, Erde Sonnensystem und das gesamte Universum in diesem Beispiel unausgesprochen als ruhendes Bezugssystem aufgefasst werden mit dem das vorgestellte Koordinatensystem verbunden ist.
Für eine vierdimensionale (raumzeitliche) Betrachtung brauchen wir ein solches reales Bezugssystem nicht. Man kann deshalb das Gedankenkonstrukt "Raumzeit" mit dem Universum in seiner Gesamtheit gleichsetzen. Das ist wohl auch der Grund weshalb es nicht schadet, der Raumzeit Realität zuzusprechen.
MfG
Harti
Grtgrt in 2068-27:Letztlich sind Raum und Zeit im Sinne dieses Modells nichts anderes als ein Bezugssystem, in das man sich Ereignisse relativ zueinander eingeordnet denkt.;
so sehe ich das im Prinzip auch.
Man muss allerdings berücksichtigen, dass wir dieses gedachte "Bezugssystem" (Koordinatensystem) in der Realität mit einem realen Bezugssystem verbinden müssen. Dies liegt daran, dass wir Bewegung als Gegensatz zu Ruhe auffassen, d.h. Bewegung und Ruhe trennen.
In den Beispielen von Einstein spielt der Bahndamm die Rolle des realen Bezugssystems; dieser Bahndamm (plus Beobachter) wird im vorgestellten Koordinatensystem ruhend vorgestellt.
In den unseren Überlegungen fehlt es häufig an der nötigen Klarheit bezhüglich dieses realen Bezugssystems.
Bei der Angabe, eine Rakete fliegt mit 1000 km/h, bleibt unklar, ob sie diese Geschwindigkeit im Verhältnis zu mir als Beobachter hat, im Verhältnis zur Erde, im Verhältnis zum Sonnensystem oder im Verhältnis zum Universum in seiner Gesamtheit. Ich gehe davon aus, dass ich, Erde Sonnensystem und das gesamte Universum in diesem Beispiel unausgesprochen als ruhendes Bezugssystem aufgefasst werden mit dem das vorgestellte Koordinatensystem verbunden ist.
Für eine vierdimensionale (raumzeitliche) Betrachtung brauchen wir ein solches reales Bezugssystem nicht. Man kann deshalb das Gedankenkonstrukt "Raumzeit" mit dem Universum in seiner Gesamtheit gleichsetzen. Das ist wohl auch der Grund weshalb es nicht schadet, der Raumzeit Realität zuzusprechen.
MfG
Harti
Beitrag 2068-43
-
Wer sich ein bestimmtes Inertialsystem S als Bezugssystem wählt, wird S relativ zu sich selbst natürlich stets ruhen sehen.
S als Bezugssystem zu wählen, soll ja gerade bewirken, dass man es als ruhendes System a u f f a s s e n kann.
Bauhof in 2068-41:
Harti in 2068-38:
Ich gehe davon aus, dass ich, Erde Sonnensystem und das gesamte Universum in diesem Beispiel unausgesprochen als ruhendes Bezugssystem aufgefasst werden mit dem das vorgestellte Koordinatensystem verbunden ist.
Im gesamten Universum gibt es kein ruhendes Bezugssystem, weder ausgesprochen noch unausgesprochen. Es gibt in der SRT nur Inertialsysteme, die sich relativ zueinander bewegen oder relativ zueinander in Ruhe sind.
M.f.G. Eugen Bauhof
Wer sich ein bestimmtes Inertialsystem S als Bezugssystem wählt, wird S relativ zu sich selbst natürlich stets ruhen sehen.
S als Bezugssystem zu wählen, soll ja gerade bewirken, dass man es als ruhendes System a u f f a s s e n kann.
Beitrag 2066-1
Warum Information sich niemals schneller als das Licht ausbreiten kann
Hin und wieder frage ich mich, warum man so sicher ist,
dass Information sich niemals schneller als das Licht ausbreiten kann.
In Jukka Maalampi: Die Weltlinie – Einstein und die moderne Physik findet sich in Abschnitt 6.2 die Begründung dafür:
dass Information sich niemals schneller als das Licht ausbreiten kann.
Zitat von Maalampi (gekürzt, nicht wörtlich):
Die Relativitätstheorie in Kombination mit der vernünftig erscheinenden Zusatzvoraussetzung, dass Informationsübertragung sämtliche Kausalitätsbeziehungen erhalten wird, führt zur Erkenntnis, dass Information sich niemals schneller als das Licht ausbreiten kann.
Wenn zwei Ereignisse an verschiedenen Orten stattfinden und keinerlei kausalen Zusammenhang aufweisen, hängt ihre zeitliche Reihenfolge von der Relativgeschwindigkeit des Beobachters in Bezug auf das betreffende Ereignispaar ab. Die chronologische Reihenfolge, von Ereignissen, die unabhängig voneinander an verschiedenen Orten stattfinden, ist relativ.
Die Erhaltung der Ursache-Folge-Beziehung gilt in der Reletivitätstheorie aber nur unter der Voraussetzung, dass sich ein Effekt mit höchstens Lichtgeschwindigkeit auf Folgen davon überträgt. Ginge es nämlich schneller, dann könnte sich aus der Sicht einiger Beobachter die Folge vor der Ursache ereignen.
Beitrag 2068-1
Fragen zur Relativität Schwarzer Löcher
In Jukka Maalampis Buch » Die Weltlinie – Einstein und die moderne Physik (2008) « liest man:
Da frägt man sich nun unwillkürlich, wie sich denn dort Längen und Horizont (des Schwarzen Loches) relativieren:
FRAGEN also:
Wenn wir uns einen Beobachter vorstellen, der direkt vor dem Ereignishorizont eines Schwarzen Loches sitzt,
Schon auf dem Horizont jedenfalls steht die Zeit offenbar still, denn:
In Jukka Maalampis Buch » Die Weltlinie – Einstein und die moderne Physik (2008) « liest man:
Zitat von Maalampi (S. 128):
Ein Schwarzes Loch ist ein extremes Beispiel für die von der Relativitätstheorie vorhergesagte Gravitations-Rotverschiebung: Je näher sich das in Bewegung setzende Licht am Ereignishorizont befindet, desto größer wird seine Wellenlänge. Die Wellenlänge des vom Horizont ausgehenden Lichtes dehnt sich ins Unendliche aus. So etwas ist gar keine Welle mehr, und auch die Energie geht gegen Null, so dass dort Strahlung aufhört Strahlung zu sein.
Da frägt man sich nun unwillkürlich, wie sich denn dort Längen und Horizont (des Schwarzen Loches) relativieren:
FRAGEN also:
Wenn wir uns einen Beobachter vorstellen, der direkt vor dem Ereignishorizont eines Schwarzen Loches sitzt,
- wie groß ist seiner Wahrnehmung nach der Radius des Schwarzen Loches bzw. sein Horizont?
- Ist es richtig, dass aus Sicht eines sich dem Horizont näherenden Beobachters beide gegen Null gehen?
- Und was genau sieht die ART als singulär (nur den Mittelpunkt des Schwarzen Lochs oder tatsächlich die gesamte Region im Inneren seines Horizonts)?
Schon auf dem Horizont jedenfalls steht die Zeit offenbar still, denn:
Zitat von Maalampi (S. 129, gekürzt, nicht wörtlich):
Wenn jemand frägt, wie man die Zeit anhalten — bzw. aus Sicht anderer ewig jung bleiben — könne, gibt es mindestens eine Antwort: Man begebe sich an den Horizont eines Schwarzen Loches. Wenn für jemand in unmittelbaren Nähe eines solchen Horizonts Wochen, Tage, oder gar nur Stunden vergehen, entspricht das auf der Erde Jahrtausenden.
Beitrag 0-212
Bewegung ist nur teilweise relativ
Unterschiedlich relative Bewegungen
Rüdiger Vaas (in seinem Buch Jenseits von Einsteins Universum, 2016, S. 192 u. 209):
Im Gegensatz zu Einsteins Ausgangspunkt und langjähriger festen Überzeugung erwiesen sich gleichförmige und beschleunigte Bewegung n i c h t als gleichermaßen relativ:
- Mit welcher Geschwindigkeit — sich zwei Körper bewegen (und ob sie sich überhaupt bewegen), lässt sich immer nur im Hinblick auf ein bestimmtes, aber beliebiges Bezugssystem sagen.
- Nur ob und wie stark eine Objekt aber beschleunigt ist, steht fest unabhängig von jeder solchen Perspektive.
Das bedeutet (z.B.): Gäbe es nur ein Raumschiff im ansonsten leeren Weltraum,
- so könnten seine Bewohner nicht sagen, wohin und wie schnell sie sich bewegen und ob überhaupt.
- Beschleunigen sie aber, so macht sich das ihnen bemerkbar durch dann auftretende Trägheitskräfte — sie sind n i c h t relativ.
Beitrag 0-511
Wie sich relative von absoluter Zeitdilatation unterscheidét
Absolute und relative Zeitdilatation
Quelle: Siegfried Petry: Spezielle Relativitätstheorie (einschließlich aller Rechnung dazu)
Siegfried Petry:
Bei den relativistischen Effekten der Zeitdilatation (Zeitverzögerung) muss strikt zwischen der absoluten und der relativen Zeitdilatation unterschieden werden.
- Die absolute Zeitdilatation — sie ist die Ursache des so genannten Zwillingsparadoxons — besteht darin, dass bei der Beschleunigung eines Bezugssystems der Gang der darin befindlichen Uhren und allgemein die Geschwindigkeit aller Abläufe verzögert werden.
Sie wurde experimentell bestätigt, indem man eine Atomuhr in einem schnellen Flugzeug auf eine Reise um die Erde schickte (Hafele-Keating-Experiment). Nach der Rückkehr ging die Uhr wieder genau so schnell wie die Vergleichsuhr am Boden, war jedoch retardiert, das heißt, ihre Anzeige war zurückgeblieben:
Die im Flugzeug transportierte Uhr — und mit ihr die Besatzung des Flugzeugs — war weniger gealtert als alles auf dem Boden zurückgebliebene.
- Die relative Zeitdilatation dagegen besteht darin, dass für die Beobachter in zwei relativ zu einander bewegten Bezugssystemen die Uhren im jeweils anderen Bezugssystem anders zu gehen scheinen als seine eigene.
Genauer: Den Dopplereffekt herausgerechnet scheint jedem Beobachter jede relativ zu ihm bewegte Uhr umso langsamer zu gehen, je schneller sie sich relativ zu ihm bewegt.
Beitrag 0-6
Beobachtete Geschwindigkeiten kleiner c (im Sinne der SRT) sind niemals wirkliche Geschwindigkeit
Beobachtete Geschwindigkeiten sind stets nur Scheingeschwindigkeit
Mit vB( X ) bezeichnen wir die Geschwindigkeit, mit der sich ein Objekt X relativ zu einem Beobachter B bewegt.
Mindestens im Rahmen Spezieller Relativitätstheorie ist dann stets
vB( X ) = vX( B )
Sind nun aber B1 und B2 relativ zueinander bewegte Beobachter ein und desselben Objektes X, so haben vB1( X ) und vB2( X ) meist unterschiedlich hohen Wert.
Aus dieser Tatsache folgt ganz klar, dass
beides stets nur S c h e i n g e s c h w i n d i g k e i t e n sind.
Weil das so ist, kann vB( X ) in Ausnahmefällen auch größer als c sein ( Beispiele dafür diskutiert der Physiker Domenico Guilini ).
Mit vB( X ) bezeichnen wir die Geschwindigkeit, mit der sich ein Objekt X relativ zu einem Beobachter B bewegt.
Mindestens im Rahmen Spezieller Relativitätstheorie ist dann stets
Sind nun aber B1 und B2 relativ zueinander bewegte Beobachter ein und desselben Objektes X, so haben vB1( X ) und vB2( X ) meist unterschiedlich hohen Wert.
Aus dieser Tatsache folgt ganz klar, dass
Weil das so ist, kann vB( X ) in Ausnahmefällen auch größer als c sein ( Beispiele dafür diskutiert der Physiker Domenico Guilini ).
Beitrag 2103-3
Beispiel einer Pseudobewegung (einer nur v i r t u e l l e n Bewegung)
Hallo Harti,
dieses Beispiel ist interessant, da es zeigt, dass nicht alles, was wir als Geschwindigkeit bezeichnen, denn auch wirklich Geschwindigkeit ist.
Es ist ja nicht so, dass sich auf dem Kreis um die Lichtquelle, auf der der Beobachter sitzt, irgend etwas bewegen würde. Was sich in den Punkten dieser Kreislinie in schneller Folge ändert, ist lediglich ihr Zustand "beleuchtet" bzw. "nicht beleuchtet" — ein Zustand also.
Ein noch interessanterer Aspekt deines Beispiels ist, dass — falls der Beobachter weiß, wie weit die Lichtquelle von ihm entfernt ist — das schnelle Wandern der Schattengrenze auf der Kreislinie Information trägt: Die Information nämlich, wie schnell sich die Lichtquelle um ihre eigene Achse dreht. Der Weg aber, auf dem diese Information ihn erreicht, ist KEIN Teil der Kreislinie, sondern Teil der Geodäte, auf der Lichtquelle und Beobachter sich befinden. Nach meiner Definition aus Beitrag 2103-1 ist die sich ständig umdefinierende Grenze zwischen Licht und Schatten also KEIN Signal — und so darf es auch nicht erstaunen, dass sie mit unbegrenzt hoher Geschwindigkeit die Kreislinie entlang wandern kann.
Wer die Kreislinie ebenso wie die Geodäte mit Straßen vergleicht, über die Fahrzeuge kommen um die Kreuzung "Beobachter" zu überqueren, wird feststellen, dass sich ständig irgendein Fahrzeug auf der Kreuzung befindet, aber doch nur eine einzige dieser zwei Straßen befahren ist: die Geodäte. Nichts bewegt sich auf der anderen Straße (obgleich all deren Punklte wieder solch stark frequentierte Kreuzungen sind).
Damit ist bewiesen: Die Grenze zwischen Licht und Schatten, die sich auf der Kreislinie zu bewegen scheint, ist kein physisches Objekt, sondern nur ein rein virtuelles im Sinn der Definition aus Beitrag 2102-26:
Gruß, grtgrt
Harti in 2103-2:
Auch ich kann mir Überlichtgeschwindigkeiten vorstellen, der keine "echte" Bewegung zugrunde liegt.
Beispiel: Der Lichtkegel einer sich um die eigene Achse drehenden Lichtquelle erscheint auf einem hinreichend großen Radius als überlichtschnell bewegt.
Hallo Harti,
dieses Beispiel ist interessant, da es zeigt, dass nicht alles, was wir als Geschwindigkeit bezeichnen, denn auch wirklich Geschwindigkeit ist.
Es ist ja nicht so, dass sich auf dem Kreis um die Lichtquelle, auf der der Beobachter sitzt, irgend etwas bewegen würde. Was sich in den Punkten dieser Kreislinie in schneller Folge ändert, ist lediglich ihr Zustand "beleuchtet" bzw. "nicht beleuchtet" — ein Zustand also.
Ein noch interessanterer Aspekt deines Beispiels ist, dass — falls der Beobachter weiß, wie weit die Lichtquelle von ihm entfernt ist — das schnelle Wandern der Schattengrenze auf der Kreislinie Information trägt: Die Information nämlich, wie schnell sich die Lichtquelle um ihre eigene Achse dreht. Der Weg aber, auf dem diese Information ihn erreicht, ist KEIN Teil der Kreislinie, sondern Teil der Geodäte, auf der Lichtquelle und Beobachter sich befinden. Nach meiner Definition aus Beitrag 2103-1 ist die sich ständig umdefinierende Grenze zwischen Licht und Schatten also KEIN Signal — und so darf es auch nicht erstaunen, dass sie mit unbegrenzt hoher Geschwindigkeit die Kreislinie entlang wandern kann.
Wer die Kreislinie ebenso wie die Geodäte mit Straßen vergleicht, über die Fahrzeuge kommen um die Kreuzung "Beobachter" zu überqueren, wird feststellen, dass sich ständig irgendein Fahrzeug auf der Kreuzung befindet, aber doch nur eine einzige dieser zwei Straßen befahren ist: die Geodäte. Nichts bewegt sich auf der anderen Straße (obgleich all deren Punklte wieder solch stark frequentierte Kreuzungen sind).
Damit ist bewiesen: Die Grenze zwischen Licht und Schatten, die sich auf der Kreislinie zu bewegen scheint, ist kein physisches Objekt, sondern nur ein rein virtuelles im Sinn der Definition aus Beitrag 2102-26:
Zitat:
Virtualität ist die Eigenschaft einer Sache, nicht in der Form zu existieren, in der sie zu existieren scheint, aber in ihrem Wesen oder ihrer Wirkung einer in dieser Form existierenden Sache zu gleichen. Das Wort führt über den französischen Begriff virtuel (fähig zu wirken, möglich).
Virtualität spezifiziert also eine gedachte oder über ihre Eigenschaften konkretisierte Entität, die zwar nicht physisch, aber doch in ihrer Funktionalität oder Wirkung vorhanden ist.
Somit ist "virtuell" nicht das Gegenteil von "real" – obwohl es fälschlicherweise oft so verwendet wird – sondern von "physisch".
Gruß, grtgrt
Beitrag 2103-4
Zwei weitere Beispiele für Überlichtgeschwindigkeit
Nun noch zwei Beispiele für
Überlichtgeschwindigkeit ,
bei denen — mir wenigstens — nicht mehr wirklich klar ist, ob man es mit realer oder nur virtueller Bewegung zu tun hat:
Quelle: Domenico Giolini: Spezielle Relativitätstheorie, 2004, Seite 109-111
bei denen — mir wenigstens — nicht mehr wirklich klar ist, ob man es mit realer oder nur virtueller Bewegung zu tun hat:
Zitat von Giolini (nicht ganz wörtlich):
Wenn man versucht, den Begriff der Geschwindigkeit auch einer Welle zuzuordnen, so gibt es dazu mehrere Möglichkeiten:
Mathematisch wird eine Welle beschrieben als Überlagerung unendlich ausgedehnter rein harmonischer Wollen von jeweils fester Frequenz und Wellenlänge. Die Phasen dieser Partialwellen breiten sich jeweils mit der sog. » Phasengeschwindigkeit « aus. Sie beträgt c/n, wo n der Brechungsindex des Mediums ist, in dem die Ausbreitung stattfindet.
Nun hängt n aber i.A. von der Frequenz der Partialwelle ab, so dass folglich die Partialwellen auch unterschiedliche Phasengeschwindigkeit haben können.
Dieses Phänomen bezeichnet man als Dispersion. Genauer: Man spricht von normaler/anormaler Dispersion, wenn n mit der Frequenz steigt/fällt (die Phasengeschwindigkeit also fällt/steigt).
Mit den Phasen einer harmonischen, unendlich weit ausgedehnten Welle kann man aber keine Signale übertragen, also darf auch die Phasengeschwindigkeit größer als c werden, was in Frequenzbereichen, in denen anormale Dispersion vorliegt, oft passiert, da dort n < 1 werden kann.
Aus harmonischen Partialwellen kann man durch Überlagerung lokalisierte Modulation oder Wellengruppen bilden, deren Schwerpunkte sich mit der sog.
» Gruppengeschwindigkeit « ausbreiten. Sie kann in nur eingeschränktem Maße zur Signalübermittlung verwendet werden, denn:Die Dispersion führt u.U. zum Zerfließen solcher Wellenpakete, so dass Signalübermittling nur so lange funktionieren kann, wie das Zerfließen nicht zu sofortiger Zerstörung der das Signal darstellenden Wellengruppe führt. Genauer:
Der mathematische Ausdruck für die Gruppengeschwindigkeit existiert zwar, doch kommt ihm in Regionen eines zu schnellen Zerfließens physikalisch nicht mehr die Bedeutung einer Signalübermittlung zu. Er kann dort größer als c werden, so dass Messungen von Gruppengeschwindigkeiten oberhalb der Lichtgeschwindigkeit immer wieder zur physikalisch nicht korrekten Behauptung führen, es seien Signale — ja sogar ganze Mozart-Symphonien — mit Überlichtgeschwindigkeit übertragen worden (siehe etwa [ G. Nimtz: ein Tunneleffekt? ]).
Uneingeschränkt zur Signalübertragung geeignet ist jeder Einschaltvorgang. Er breitet sich mit der sog. » Frontgeschwindigkeit « aus. Das ist die Geschwindigkeit, mit der sich der Wellenkopf bewegt, jene Stelle also, an der die Welle von einer schon einige Zeit andauernden Nullamplitude zu einer von Null verschiedenen Amplitude abhebt. Man denke etwa an das Morsen, wo Strich und Punkt mehr oder weniger lange Signale sind, die durch Pausen absoluter Ruhe getrennt sind.
Es gibt dann noch die » Energiegeschwindigkeit «, mit der sich Energie in einer Welle ausbreiten kann. Sie muss mit keiner der oben genannten Geschwindigkeiten übereinstimmen und kann niemals größer als c sein.
FAZIT:
- Phasen- und Gruppengeschwindigkeiten größer c widersprechen der SRT nicht.
- Anders liegt die Sache bei Signal- und Energiegeschwindigkeiten: Sie würden, wenn sie größer als c sein könnten, die SRT in ernsthafte Schwierigkeiten bringen.
Quelle: Domenico Giolini: Spezielle Relativitätstheorie, 2004, Seite 109-111
Beitrag 2103-1
Überlichtgeschwindigkeit — eine Klarstellung und 2 Beispiele
Überlichtgeschwindigkeit – es gibt sie auch in SRT und ART
Ein weit verbreiteter Irrtum besteht darin, zu glauben, dass es keine Geschwindigkeiten höher als die des Lichts gibt.
Tatsächlich gibt es beliebig hohe Geschwindigkeiten auch im Rahmen der beiden Relativitätstheorien. Beide — die SRT und auch die ART — beweisen lediglich, dass kein Signal sich schneller als das Licht bewegen kann.
Signal in diesem Sinne ist alles,
das sich auf der Geodäte der Raumzeit bewegt, die den Beobachter mit dem beobachteten Objekt verbindet
( in der SRT also auf einer Geraden, die durch den Beobachter führt ).
Eine gut verständliche Begründung — und auch zwei Beispiele — finden sich auf den Seiten 106 bis 111 des Buches Spezielle Relativitätstheorie des Physikers Domenico Giulini (erschienen 2004 im Fischer Taschenbuch Verlag):
Hier nun die beiden Beispiele für tatsächlich b e o b a c h t b a r e Überlichtgeschwindigkeit, die Giulini im Detail diskutiert:
Vorsicht aber: B e o b a c h t e t e Geschwindigkeiten sind Scheingeschwindigkeiten, die für zueinander bewegte Beobchter u n t e r s c h i e d l i c h hohen Wert haben (als mit Sicherheit keine reale Geschwindigkeit darstellen).
Beispiel 1 (nachgerechnet auf Basis der SRT):
Beispiel 2 (auf Basis ART, da durch astronomische Beobachtung entdeckt):
PS 1: Diese Beispiele zeigen einmal mehr, dass — worauf ich hier im Forum schon mehrmals zu sprechen kam — durch Beobachter gemessene Geschwindigkeiten stets nur S i c h t auf eine Signalgeschwindigkeit sein können (niemals aber wirklich reale Geschwindigkeiten sind). Mit anderen Worten:
Es gilt zu unterscheiden zwischen
Erst wer das verstanden hat, kann verstanden haben, wie die SRT denn nun wirklich argumentiert und was ihre Aussagen tatsächlich bedeuten.
PS 2: Man sollte sich zudem klar machen, dass die Raumzeit — ausgestattet mit der Minkowski-Metrik — nur eine einzige r e a l e Geschwindigkeit kennt: die des Lichts.
Denn alles, was man sonst noch so an Geschwindigkeiten kennt, sind einfach nur beobachter-spezifische S i c h t e n , die sich ergeben
Ein weit verbreiteter Irrtum besteht darin, zu glauben, dass es keine Geschwindigkeiten höher als die des Lichts gibt.
Tatsächlich gibt es beliebig hohe Geschwindigkeiten auch im Rahmen der beiden Relativitätstheorien. Beide — die SRT und auch die ART — beweisen lediglich, dass kein Signal sich schneller als das Licht bewegen kann.
das sich auf der Geodäte der Raumzeit bewegt, die den Beobachter mit dem beobachteten Objekt verbindet
( in der SRT also auf einer Geraden, die durch den Beobachter führt ).
Eine gut verständliche Begründung — und auch zwei Beispiele — finden sich auf den Seiten 106 bis 111 des Buches Spezielle Relativitätstheorie des Physikers Domenico Giulini (erschienen 2004 im Fischer Taschenbuch Verlag):
Zitat von Giulini:
Wird die Frage » Gibt es Überlichtgeschwindigkeiten? « in dieser Allgemeinheit gestellt, so muss sie mit einem klaren JA beantwortet werden:
Nur bestimmten Ausbreitungsphänomenen setzt die SRT den Wert c als Grenze. Dies betrifft ... allgemein alle Prozesse, die zumindest im Prinzip einer Signalübertragung dienen können, wobei man hier allerdings eine sorgfältige Definition von » Signal « anfügen müsste. Auf jeden Fall würde eine Signalausbreitung mit Überlichtgeschwindigkeit innerhalb der SRT zu Widersprüchen in Kausalitätsverhältnissen führen.
Hier nun die beiden Beispiele für tatsächlich b e o b a c h t b a r e Überlichtgeschwindigkeit, die Giulini im Detail diskutiert:
Vorsicht aber: B e o b a c h t e t e Geschwindigkeiten sind Scheingeschwindigkeiten, die für zueinander bewegte Beobchter u n t e r s c h i e d l i c h hohen Wert haben (als mit Sicherheit keine reale Geschwindigkeit darstellen).
Beispiel 1 (nachgerechnet auf Basis der SRT):
- Giulini betrachtet einen Beobachter B, der im Ursprung eines Inertialsystems sitzt und ein Objekt X beobachtet, das sich auf einer Geraden mit gleichförmiger Geschwindigkeit bewegt. Diese Gerade führe nicht durch den Beobachter, wohl aber durch einen Punkt P. Bezeichnet nun a den spitzen Winkel zwischen dieser Geraden und der Strecke von B nach P, so kommt Giulini über einige wenige Rechenschritte hin zur Aussage, dass für die durch B beobachtete Geschwindigkeit v(B) des Objekts X
- gilt, wenn man
- setzt und hierbei unter v die Geschwindigkeit versteht, mit der sich X als Signal seiner Bahn entlang durch den 3-dimensionalen Raum bewegt.
- Für ein festes Verhältnis v/c und variablen Winkel a erreicht die Funktion s(a,v) ihr Maximum bei cos(a) = v/c . Dort ist dann also
- was für v gegen c nach unendlich strebt, so dass also tatsächlich v(B) auch weit größer als c werden kann.
Beispiel 2 (auf Basis ART, da durch astronomische Beobachtung entdeckt):
Zitat von Giulini:Heute kennt man in der Astronomie zahlreiche Beispiel für diesen Effekt [ beobachteter Überlichtgeschwindigkeit ].
Ein besonders eindrucksvolles liefert die Galaxie M87, die sich in einer Entfernung von 60 Mio Lichtjahren von uns im Virgohaufen befindet. Aus ihrem Zentrum werden Gasströme entlang sog. Jets auf einer Länge von 5000 Lichtjahren ins All geschleudert, deren gemessene visuelle Geschwindigkeit v(B) die 6-fache Lichtgeschwindigkeit erreichen!.
Getrieben werden diese Jets wahrscheinlich durch ein im Zentrum der Galaxie vorhandenes supermassives Schwarzes Loch. Man schätzt die eigentliche Geschwindigkeit v der Gasströmung [ die also, die sie als Signal hat ] auf höchstens 98% der Lichtgeschwindigkeit.
PS 1: Diese Beispiele zeigen einmal mehr, dass — worauf ich hier im Forum schon mehrmals zu sprechen kam — durch Beobachter gemessene Geschwindigkeiten stets nur S i c h t auf eine Signalgeschwindigkeit sein können (niemals aber wirklich reale Geschwindigkeiten sind). Mit anderen Worten:
Es gilt zu unterscheiden zwischen
- scheinbarer ( d.h. beobachteter ) Geschwindigkeit einerseits und
- Signalgeschwindigkeit andererseits (nur sie kann niemals höher als Lichtgeschwindigkeit sein; ihre Richtung ist stets tangential zu einer Geodäte).
Erst wer das verstanden hat, kann verstanden haben, wie die SRT denn nun wirklich argumentiert und was ihre Aussagen tatsächlich bedeuten.
PS 2: Man sollte sich zudem klar machen, dass die Raumzeit — ausgestattet mit der Minkowski-Metrik — nur eine einzige r e a l e Geschwindigkeit kennt: die des Lichts.
Denn alles, was man sonst noch so an Geschwindigkeiten kennt, sind einfach nur beobachter-spezifische S i c h t e n , die sich ergeben
- entweder als Projektion von Signalgeschwindigkeit in der Raumzeit auf den 3-dimensionalen Raum
- und/oder als Schrumpfen oder Wachsen von Abständen (pro Zeiteinheit) zweier vom Beobachter ins Auge gefasster Objekte aus der spezifischen Perspektive des Beobachters und seiner Uhr heraus.
Beitrag 1981-1
Zweite Frage
Eine der wichtigsten Fragen, die uns Physiker noch NICHT beantworten können, ist die Frage nach der Natur der Zeit. Bisher weiß man nur:
Es gibt KEINEN universellen zeitlichen Abstandsbegriff (und auch keine aus Sicht aller Betrachter gegebene Gleichzeitigkeit zweier Ereignisse).
Wie aber steht es mit einem universellen räumlichen Abstandsbegriff?
Hat sich jemand diese Frage überhaupt schon mal gestellt?
Eine der wichtigsten Fragen, die uns Physiker noch NICHT beantworten können, ist die Frage nach der Natur der Zeit. Bisher weiß man nur:
Es gibt KEINEN universellen zeitlichen Abstandsbegriff (und auch keine aus Sicht aller Betrachter gegebene Gleichzeitigkeit zweier Ereignisse).
Wie aber steht es mit einem universellen räumlichen Abstandsbegriff?
Hat sich jemand diese Frage überhaupt schon mal gestellt?
Beitrag 1981-2
Die klassische Antwort
Hallo Grtgrt,
ich denke, es gibt ebenso keinen universellen Abstandsbegriff.
Ich verstehe die SRT so, dass sowohl gemessene Zeitintervalle wie auch gemessene Raumintervalle abhängig vom gewählten Inertialsystem sind.
Erst Raumzeitintervalle sind unabhängig vom Beobachter invariant. Ein Indiz dafür, dass das Universum erst verstanden werden kann, wenn man die Raumzeit als eine Einheit begreift.
Das zeigt doch schon die Lorentztransformation:
Entfernungen schrumpfen in Bewegungsrichtung im Verhältnis zum Beobachter, welcher zum Ziel der Bewegung ruht.
Ein Beobachter, welcher zu einem entfernten Planeten ruht, wird eine größere Entfernung ermitteln, als ein Beobachter, welcher sich auf den Planeten zubewegt.
mfg okotombrok�
Grtgrt aus 1981-1:Eine der wichtigsten Fragen, die uns Physiker noch NICHT beantworten können, ist die Frage nach der Natur der Zeit. Bisher weiß man nur:
Es gibt KEINEN universellen zeitlichen Abstandsbegriff (und auch keine aus Sicht aller Betrachter gegebene Gleichzeitigkeit zweier Ereignisse).
Wie aber steht es mit einem universellen räumlichen Abstandsbegriff?
ich denke, es gibt ebenso keinen universellen Abstandsbegriff.
Ich verstehe die SRT so, dass sowohl gemessene Zeitintervalle wie auch gemessene Raumintervalle abhängig vom gewählten Inertialsystem sind.
Erst Raumzeitintervalle sind unabhängig vom Beobachter invariant. Ein Indiz dafür, dass das Universum erst verstanden werden kann, wenn man die Raumzeit als eine Einheit begreift.
Das zeigt doch schon die Lorentztransformation:
Entfernungen schrumpfen in Bewegungsrichtung im Verhältnis zum Beobachter, welcher zum Ziel der Bewegung ruht.
Ein Beobachter, welcher zu einem entfernten Planeten ruht, wird eine größere Entfernung ermitteln, als ein Beobachter, welcher sich auf den Planeten zubewegt.
mfg okotombrok�
Beitrag 1981-4
Die vielleicht bessere (neue) Deutung
Hallo Okotombrok,
hallo Henry:
So wirklich gut erklärt ist die Situation hierdurch keineswegs. Man kann sich ja durchaus fragen:
Was genau wollen wir denn eigentlich unter der Entfernung des Beobachters vom Planeten verstehen, wenn der Beobachter auf den Planeten zurast?
Schließlich und endlich benötigt die Messung ja Zeit, und während dieser Zeit kommen Planet und Beobachter einander näher.
Als was also soll der Abstand der beiden dann definiert sein? Als der zu Beginn der Messung oder als der zu Ende der Messung? Oder als Durchschnitt davon?
Und können sich Beobachter und Planet denn überhaupt auf einen gemeinsamen Zeitpunkt "Beginn der Messung" verständigen, wo wir doch wissen, dass es einen wohldefinierten Begriff "gleichzeitig" nach der ART gar nicht geben kann?
Die Situation wird vielleicht klarer, wenn wir noch andere Beispiele betrachten:
Der Konstanz der Lichtgeschwindigkeit wegen wird diese Situation üblicherweise so gedeutet, dass man sagt, aus Sicht von A vergehe für B die Zeit langsamer als für A.
Stimmt das aber wirklich?
Muss man nicht genauer sein und sagen, dass A das Photon auf einem Weg von Q nach Q hat wandern sehen, der ganz andere Form und deswegen auch andere Länge hatte als der Weg, auf dem B es wandern sah.
Diese Interpretation ist sicher auch richtig, denn sie wird gestützt durch die Tatsache, dass die Länge beider Wege über dieselbe Metrik gemessen wurde (über die auf jedem reellen 3-dimensionalen Vektorraum gleich definierten euklidischen Metrik).
Wer das so sieht, wird nicht mehr sagen, dass die Zeit oder die Metrik des Raumes relativ sei. Man würde stattdessen anerkennen, dass der Weg, den das Photon nahm, aus Sicht von A ein anderer war als aus Sicht von B.
Diese Interpretation macht auch dann noch Sinn, wenn der Lastwagen sich mit zunehmender oder abnehmender Geschwindigkeit bewegt (beschleunigt also).
Sie macht auch Sinn, wo es statt um räumliche um zeitliche Abstände geht. Hier ein Beispiel dazu:
Man interpretiert das üblicherweise so, dass man sagt, für die bewegte Uhr sei die Zeit langsamer vergangen.
Und wieder kann man umgekehrt auch sagen: Beide Uhren gingen gleich schnell, haben aber unterschiedliche Wege durch die Zeit von E1 nach E2 gestoppt.
Diese Interpretation des Versuchsergebnisses entspricht den Tatsachen besser, denn der Weg durch die Raumzeit, den die eine Uhr ging, hat mehr durch die Zeit und weniger durch den Raum geführt als der Weg, den die andere Uhr nahm (jene, die im Flugzeug ganz anderen Beschleunigungen ausgesetzt war).
Fazit also:
Wo bei Messung von zeitlichen oder räumlichen Abständen unterschiedliche Beobachter zu widersprüchlichen Aussagen gelangen, sind solche Widersprüche nicht auf unterschiedliche Metrik zurückzuführen, sondern einfach nur darauf, dass jede der beiden Messungen einen anderen Weg zwischen den beiden betrachteten Punkten der Raumzeit zum Gegenstand hatte.
Und wirklich: In jedem Raum, der mehr als nur eine Dimension hat, gibt es zwischen je zwei Punkten diesen Raumes beliebig viele unterschiedlich lange Wege.
Dies nicht zu vergessen und sich Rechenschaft darüber zu geben, von welchem dieser Wege man im konkreten Fall spricht, kann nicht schaden.
Gruß, grtgrt
Okotombrok aus 1981-2:
Entfernungen schrumpfen in Bewegungsrichtung im Verhältnis zum Beobachter, welcher zum Ziel der Bewegung ruht.
Ein Beobachter, welcher zu einem entfernten Planeten ruht, wird eine größere Entfernung ermitteln, als ein Beobachter, welcher sich auf den Planeten zubewegt.
Hallo Okotombrok,
hallo Henry:
So wirklich gut erklärt ist die Situation hierdurch keineswegs. Man kann sich ja durchaus fragen:
Was genau wollen wir denn eigentlich unter der Entfernung des Beobachters vom Planeten verstehen, wenn der Beobachter auf den Planeten zurast?
Schließlich und endlich benötigt die Messung ja Zeit, und während dieser Zeit kommen Planet und Beobachter einander näher.
Als was also soll der Abstand der beiden dann definiert sein? Als der zu Beginn der Messung oder als der zu Ende der Messung? Oder als Durchschnitt davon?
Und können sich Beobachter und Planet denn überhaupt auf einen gemeinsamen Zeitpunkt "Beginn der Messung" verständigen, wo wir doch wissen, dass es einen wohldefinierten Begriff "gleichzeitig" nach der ART gar nicht geben kann?
Die Situation wird vielleicht klarer, wenn wir noch andere Beispiele betrachten:
- Sei dazu A eine Person, die an einer Straße sitzt, auf der ein Lastwagen fährt, auf dessen Ladefläche eine Person B sitzt, die eine Lichtuhr festhält. Diese Uhr bestehe aus einem 2 Meter hohen, senkrecht neben ihr auf einer Lichtquelle Q stehenden Glasstab, der ganz oben in einem Spiegel endet. Wenn Q ein Photon aussendet, wandert das durch den Stab nach oben, wird dort am Spiegel reflektiert, und kommt so zurück zur Lichtquelle. Aus Sicht von B hat dieses Lichtquant dann also zwei Mal ein und dasselbe Stück einer Geraden durchlaufen: einen geschlossenen Weg Q nach Q von insgesamt genau 4 Metern Länge.
- Relativ zu A aber hat Q sich bewegt, und deswegen hat das Photon aus Sicht von A einen etwas längeren Weg zurückgelegt: Er war nicht geschlossen, denn er war gegeben durch die beiden etwas über 2 Meter langen Seiten eines gleichschenkeligen Dreiecks, dessen Höhe 2 Meter betrug.
Der Konstanz der Lichtgeschwindigkeit wegen wird diese Situation üblicherweise so gedeutet, dass man sagt, aus Sicht von A vergehe für B die Zeit langsamer als für A.
Stimmt das aber wirklich?
Muss man nicht genauer sein und sagen, dass A das Photon auf einem Weg von Q nach Q hat wandern sehen, der ganz andere Form und deswegen auch andere Länge hatte als der Weg, auf dem B es wandern sah.
Diese Interpretation ist sicher auch richtig, denn sie wird gestützt durch die Tatsache, dass die Länge beider Wege über dieselbe Metrik gemessen wurde (über die auf jedem reellen 3-dimensionalen Vektorraum gleich definierten euklidischen Metrik).
Wer das so sieht, wird nicht mehr sagen, dass die Zeit oder die Metrik des Raumes relativ sei. Man würde stattdessen anerkennen, dass der Weg, den das Photon nahm, aus Sicht von A ein anderer war als aus Sicht von B.
Diese Interpretation macht auch dann noch Sinn, wenn der Lastwagen sich mit zunehmender oder abnehmender Geschwindigkeit bewegt (beschleunigt also).
Sie macht auch Sinn, wo es statt um räumliche um zeitliche Abstände geht. Hier ein Beispiel dazu:
- Wir nehmen zwei identisch gebaute Atomuhren, stellen sie nebeneinander und garantieren, dass beide gleichzeitig starten (Ereignis E1).
- Eine dieser Uhren lassen wir stehen, die andere fliegen wir mit einem schnellen Flugzeug einige Male um die Erde, um sie danach wieder an ihren alten Platz neben die erste zu stellen und dann beide gleichzeitig anzuhalten (Ereignis E2).
- Wie die ART uns lehrt — und wie mehrfache Durchführung dieses Experiments ja auch tatsächlich bewiesen hat — werden die Uhren dann NICHT mehr gleiche Aussage machen: Auf der um die Erde geflogenen wird weniger Zeit vergangen sein.
Man interpretiert das üblicherweise so, dass man sagt, für die bewegte Uhr sei die Zeit langsamer vergangen.
Und wieder kann man umgekehrt auch sagen: Beide Uhren gingen gleich schnell, haben aber unterschiedliche Wege durch die Zeit von E1 nach E2 gestoppt.
Diese Interpretation des Versuchsergebnisses entspricht den Tatsachen besser, denn der Weg durch die Raumzeit, den die eine Uhr ging, hat mehr durch die Zeit und weniger durch den Raum geführt als der Weg, den die andere Uhr nahm (jene, die im Flugzeug ganz anderen Beschleunigungen ausgesetzt war).
Fazit also:
Wo bei Messung von zeitlichen oder räumlichen Abständen unterschiedliche Beobachter zu widersprüchlichen Aussagen gelangen, sind solche Widersprüche nicht auf unterschiedliche Metrik zurückzuführen, sondern einfach nur darauf, dass jede der beiden Messungen einen anderen Weg zwischen den beiden betrachteten Punkten der Raumzeit zum Gegenstand hatte.
Und wirklich: In jedem Raum, der mehr als nur eine Dimension hat, gibt es zwischen je zwei Punkten diesen Raumes beliebig viele unterschiedlich lange Wege.
Dies nicht zu vergessen und sich Rechenschaft darüber zu geben, von welchem dieser Wege man im konkreten Fall spricht, kann nicht schaden.
Gruß, grtgrt
Beitrag 1981-20
-
Hi Okotombrok,
du verstehst mich hier wirklich falsch, denn ich will keineswegs irgend einen Teil der Relativitätstheorie in Frage stellen.
Mir fällt lediglich auf, dass die klassische Deutung dessen, was die SRT uns lehrt, nicht die einzig mögliche ist.
Genauer:
Was die SRT uns zeigt, ist eine gewisse Relativität (die Relativität von Raum und Zeit).
Mir aber fällt auf, dass man die daraus resultierenden Unterschiede in der Sicht gegeneinander bewegter Betrachter auch so deuten kann, dass
statt Raum und Zeit wirklich nur die Wege, an die man denkt, relativ sind.
Das erscheint mir deswegen spannend, da man auf diese Weise nicht mehr von Uhren sprechen muss, die verschieden schnell gehen obgleich sie doch absolut gleich gebaut sind. Man spricht stattdessen von unterschiedlich langen Wegen zwischen je zwei Ereignissen (von Wegen, die i.A. durch die Raumzeit führen, also nicht nur durch den Raum).
Dies führt zu einer nahtloseren Einbettung der SRT in die ART (auch wenn jene Wege in Abwesenheit von Beschleunigung – im Spezialfall der SRT also – tatsächlich nur durch den Raum führen).
Zudem gibt es unter dieser neuen Deutung keinerlei Grund mehr, die Zeit als verzweigungsfrei sehen zu müssen: Unter meiner Deutung der Relativität können Wege durch die Zeit sämtliche Eigenschaften haben, die auch Wege durch den Raum haben. Insbesondere können zwei Punkte der Raumzeit – zwei Ereignisse also – durch zeitlich unterschiedlich lange Wege verbunden sein. Wer den zeitlich kürzesten genommen hat, so sieht man dann sofort, wird am wenigsten gealtert sein. Alterung lässt sich dann, wie das ja auch ganz natürlich ist, interpretieren als ein Verbrauch von Resourcen, der bei gleichförmiger Bewegung proportional zur Länge des jeweils gewählten Weges ist, ansonsten aber zudem noch durch Kräfte mitbestimmt wird, die den Reisenden beschleunigen oder abbremsen.
Kurz: Ich schlage wirklich nur eine andere Deutung der durch Einstein aufgedeckten Relativität vor, aber keine andere Theorie. Sämtliche Formeln bleiben unverändert.
Relativ ist dann nur der Weg, der dem Betrachter am einfachsten erscheint,
aber nicht mehr der Raum, die Zeit, oder die zur Bestimmung seiner Länge verwendete Elle (= Metrik, Meter, Uhr).
Beste Grüße,
grtgrt
Okotombrok aus 1981-17:
Die Längenkontraktion wie auch die Zeitdilatation sind experimentell außerordentlich gut bestätigt und werden mit der SRT korrekt beschrieben. Ich verstehe nicht, wie du die Relativität räumlicher Abstände als in der Physik als ungeklärt betrachten kannst. Oder habe ich dich falsch verstanden?
Hi Okotombrok,
du verstehst mich hier wirklich falsch, denn ich will keineswegs irgend einen Teil der Relativitätstheorie in Frage stellen.
Genauer:
Was die SRT uns zeigt, ist eine gewisse Relativität (die Relativität von Raum und Zeit).
Mir aber fällt auf, dass man die daraus resultierenden Unterschiede in der Sicht gegeneinander bewegter Betrachter auch so deuten kann, dass
Das erscheint mir deswegen spannend, da man auf diese Weise nicht mehr von Uhren sprechen muss, die verschieden schnell gehen obgleich sie doch absolut gleich gebaut sind. Man spricht stattdessen von unterschiedlich langen Wegen zwischen je zwei Ereignissen (von Wegen, die i.A. durch die Raumzeit führen, also nicht nur durch den Raum).
Dies führt zu einer nahtloseren Einbettung der SRT in die ART (auch wenn jene Wege in Abwesenheit von Beschleunigung – im Spezialfall der SRT also – tatsächlich nur durch den Raum führen).
Zudem gibt es unter dieser neuen Deutung keinerlei Grund mehr, die Zeit als verzweigungsfrei sehen zu müssen: Unter meiner Deutung der Relativität können Wege durch die Zeit sämtliche Eigenschaften haben, die auch Wege durch den Raum haben. Insbesondere können zwei Punkte der Raumzeit – zwei Ereignisse also – durch zeitlich unterschiedlich lange Wege verbunden sein. Wer den zeitlich kürzesten genommen hat, so sieht man dann sofort, wird am wenigsten gealtert sein. Alterung lässt sich dann, wie das ja auch ganz natürlich ist, interpretieren als ein Verbrauch von Resourcen, der bei gleichförmiger Bewegung proportional zur Länge des jeweils gewählten Weges ist, ansonsten aber zudem noch durch Kräfte mitbestimmt wird, die den Reisenden beschleunigen oder abbremsen.
Kurz: Ich schlage wirklich nur eine andere Deutung der durch Einstein aufgedeckten Relativität vor, aber keine andere Theorie. Sämtliche Formeln bleiben unverändert.
aber nicht mehr der Raum, die Zeit, oder die zur Bestimmung seiner Länge verwendete Elle (= Metrik, Meter, Uhr).
Beste Grüße,
grtgrt
Beitrag 1981-24
-
Hi Eugen,
was du in den letzten 3 Zeilen dieses Zitats sagst, ist absolut richtig und GENAU das, was ich auch sage.
Nur deine erste Aussage (die in der Zeile davor) ist falsch, denn das Beispiel mit den Zwillingsbrüdern illustriert die ART ( NICHT aber die SRT !! ). Das liegt daran, dass der die Erde verlassende und dann zu ihr zurückkehrende Zwillingsbruder Beschleunigungskräften ausgesetzt ist.
Wenn du also argumentieren möchtest, dass meine Deutung von Relativität der SRT widerspricht, dann musst da zwei gleichförmig zueinander bewegte Personen betrachten. Tust du das aber, so sagt die SRT, dass aus Sicht JEDER der beiden, die Zeit beim jeweils anderen langsamer vergeht. ( Das scheint rein logisch ein Widerspruch zu sein, die Tatsache aber, dass der durch meine Deutung aufgelöst wird, zeigt recht deutlich ihren Wert. )
Beste Grüße,
grtgrt
Bauhof aus 1981-21:Hallo Grtgrt,
wenn du Einsteins SRT akzeptierst, dann musst du auch folgendes akzeptieren:
Die Uhren gehen nicht unterschiedlich schnell, sondern die Zeit selbst verläuft beim bewegten Zwillingsbruder anders ab als bei dem auf der Erde ruhendem Zwillingsbruder. Die Uhr des reisenden Zwillingsbruders hat den gleichen Gang wie die Uhr seines ruhenden Zwillingsbruders, sie zeigt die während seiner Reise verflossene Eigenzeit an.
Hi Eugen,
was du in den letzten 3 Zeilen dieses Zitats sagst, ist absolut richtig und GENAU das, was ich auch sage.
Nur deine erste Aussage (die in der Zeile davor) ist falsch, denn das Beispiel mit den Zwillingsbrüdern illustriert die ART ( NICHT aber die SRT !! ). Das liegt daran, dass der die Erde verlassende und dann zu ihr zurückkehrende Zwillingsbruder Beschleunigungskräften ausgesetzt ist.
Wenn du also argumentieren möchtest, dass meine Deutung von Relativität der SRT widerspricht, dann musst da zwei gleichförmig zueinander bewegte Personen betrachten. Tust du das aber, so sagt die SRT, dass aus Sicht JEDER der beiden, die Zeit beim jeweils anderen langsamer vergeht. ( Das scheint rein logisch ein Widerspruch zu sein, die Tatsache aber, dass der durch meine Deutung aufgelöst wird, zeigt recht deutlich ihren Wert. )
Beste Grüße,
grtgrt
Beitrag 1981-29
-
Hi E...:
Du hast recht: Es geht um die Eigenzeit (= die wegspezifische Zeit). Genau das sagt meine Deutung ja.
Wer einen Weg geht, der 33 cm höher liegt als ein anderer, uns dazu parallel erscheinender, ist einer geringeren Gravitationskraft ausgesetzt (geht also einen Weg anderer Charakteristik, der dann eben auch eine andere Eigenzeit hat).
Dass Wege, auf denen größere Beschleunigungskraft wirkt, kürzere Wege durch die Raumzeit darstellen, kann man sich sehr gut vorstellen: Geht die Stärke jener Kraft nämlich gegen Unendlich, so bedeutet das, dass jener Weg sich schließlich in immer engere Umgebung des Mittelpunktes eines Schwarzes Loches verschiebt — und damit ganz klar immer kürzer wird.
Beste Grüße,
grtgrt
E... aus 1981-22:
Da geht es um die Eigenzeit.
Damit Du aber etwas anschaulicher begutachten kannst, dass Deine "neue" Definition nicht tragfähig ist, schau mal hier nach...
http://www.faz.net/aktuell/wissen/physik-chemie/all...
Wenn ein Höhenunterschied von 33 cm im Schwerefeld unseres Planeten ausreicht, um unterschiedliche Eigenzeiten zu verursachen, kann Deine Definition nicht zutreffend sein.
Hi E...:
Du hast recht: Es geht um die Eigenzeit (= die wegspezifische Zeit). Genau das sagt meine Deutung ja.
Wer einen Weg geht, der 33 cm höher liegt als ein anderer, uns dazu parallel erscheinender, ist einer geringeren Gravitationskraft ausgesetzt (geht also einen Weg anderer Charakteristik, der dann eben auch eine andere Eigenzeit hat).
Dass Wege, auf denen größere Beschleunigungskraft wirkt, kürzere Wege durch die Raumzeit darstellen, kann man sich sehr gut vorstellen: Geht die Stärke jener Kraft nämlich gegen Unendlich, so bedeutet das, dass jener Weg sich schließlich in immer engere Umgebung des Mittelpunktes eines Schwarzes Loches verschiebt — und damit ganz klar immer kürzer wird.
Beste Grüße,
grtgrt
Beitrag 1981-39
Beschleunigungskräfte — und nur sie — machen Uhren langsamer
Tatsachen sind:
Beschleunigungskräfte (und nur sie) machen Uhren langsamer.
Zueinander gleichförmig bewegte Uhren haben lediglich den Eindruck, die jeweils andere würde langsamer gehen:
Tatsächlich aber gehen sie synchron.
Tatsachen sind:
Tatsächlich aber gehen sie synchron.
Beitrag 1981-55
Was ist Gravitation?
Hi Eugen,
ich bin fest davon überzeugt, dass meine Behauptung richtig ist, mehr noch: dass Gravitation und Beschleunigung ein und dasselbe sind.
Beschleunigungskräfte kennen wir als
Je größer die Summe dieser Kräfte ist, desto langsamer vergeht die Zeit,
und umgekehrt: Dehnung der Zeit erzeugt Gravitation.
Wie Gravitation (Beschleunigungskräfte also) die Raumzeit krümmen, versucht man meist über das sog. Gummituchmodell zu illustrieren.
Es macht deswegen Sinn zu sagen:
Gravitation = das Feld aller Energie-Impuls-Tensoren (in unserem Universum)
grtgrt
bezugnehmend auf Joachim Schulz und dessen Artikel » Gravitation - Was krümmt den Raum? «
Bauhof aus 1981-47:
dass Beschleunigungskräfte (und nur sie) Uhren langsamer machen, schrieb nicht Henry, sondern Grtgrt.
Ungeachtet dessen ist die Behauptung falsch.
Hi Eugen,
ich bin fest davon überzeugt, dass meine Behauptung richtig ist, mehr noch: dass Gravitation und Beschleunigung ein und dasselbe sind.
Beschleunigungskräfte kennen wir als
- die G r a v i t a t i o n s k r a f t (sie erzeugt Beschleunigung)
- die T r ä g h e i t s k r a f t (sie entsteht als Folge von Beschleunigung)
- die F l i e h k r a f t (sie entsteht ebenfalls als Folge von Beschleunigung).
und umgekehrt: Dehnung der Zeit erzeugt Gravitation.
Zitat von Joachim Schulz:
Um zu verstehen, warum Dehnung der Zeit zu Gravitation führt, muss man von der Vorstellung von drei Raum- und einer Zeitdimensionen auf eine 4-dimensionale Vorstellung wechseln. In dieser Vorstellung bewegt sich alles durch die Zeit. Selbst ein ruhendes Objekt eilt im Sauseschritt durch die Dimension Zeit. Und diese Bewegung durch die gleichmäßig vergehende Zeit ist eine gerade Strecke. Versucht nun ein Objekt in der gekrümmten Zeit auf einer Geraden zu laufen, so wird daraus eine Kurve. Eine Kurve in der Raum-Zeit ist aber kein Ruhezustand mehr sondern eine beschleunigte Bewegung. So kommt die Beschleunigung eines Objektes in einer gekrümmten Raum-Zeit zustande. Und das nicht nur für schwere Objekte, sondern auch für Lichtwellen und alles, was sich durch Zeit und Raum bewegt.
Wie Gravitation (Beschleunigungskräfte also) die Raumzeit krümmen, versucht man meist über das sog. Gummituchmodell zu illustrieren.
Zitat von Joachim Schulz:
Das Gummituchmodell erklärt aber eines gar nicht: Warum krümmt sich der Raum eigentlich?
Ist es die Ruhemasse der Elementarteilchen, die sich in einem Objekt befinden? Das kann nicht sein, denn dann könnte Licht nicht an der Gravitation beteiligt sein. Die Elementarteilchen des Lichts, die Photonen, sind bekanntlich masselos, der Einfluss von Gravitation auf Licht lässt sich aber leicht nachweisen. Ist es also die Gesamtmasse inklusive Bewegungsenergie, die den Raum krümmt? Das würde der allgemeinen Relativitätstheorie, die unabhängig von Beobachtern formulierbar sein muss, nicht gerecht werden. Bewegungsenergie ist eine relative Größe.
Tatsächlich ist es eine etwas kompliziertere Größe, die den Raum krümmt: Der Energie-Impuls-Tensor.
Kennt man von einer Materieverteilung das Feld von Energie-Impuls-Tensoren, so weiß man alles über die Massen-, Energie-, Impuls- und Druckverteilung in dieser Masse.
Es macht deswegen Sinn zu sagen:
grtgrt
bezugnehmend auf Joachim Schulz und dessen Artikel » Gravitation - Was krümmt den Raum? «
Beitrag 1981-63
-
Das, Henry, glaube ich nicht,
denn ich verstehe Joachim Schulz dahingegehend, dass die Begriffe "Gravitation", "Gravitationskraft", "Beschleunigung", "Trägheitskraft", "Fliehkraft" einfach nur Namen für makroskopische Sichten auf riesige Mengen elementarer Energie-Impulse sind.
Was die Raumzeit krümmt, sind letztlich jene Energie-Impulse (und das ohne Rücksicht darauf, was sie verursacht hat).
Gruß, grtgrt
PS: Unter einem elementaren Energie-Impuls verstehe ich den Impuls eines Elementarteilchens.
Henry aus 1981-56:Zitat von grtgrt:
Du verwechselst Ursache und Wirkung, außerdem verwechselst du die mathematische Beschreibung mit der Realität.
Das, Henry, glaube ich nicht,
denn ich verstehe Joachim Schulz dahingegehend, dass die Begriffe "Gravitation", "Gravitationskraft", "Beschleunigung", "Trägheitskraft", "Fliehkraft" einfach nur Namen für makroskopische Sichten auf riesige Mengen elementarer Energie-Impulse sind.
Was die Raumzeit krümmt, sind letztlich jene Energie-Impulse (und das ohne Rücksicht darauf, was sie verursacht hat).
Gruß, grtgrt
PS: Unter einem elementaren Energie-Impuls verstehe ich den Impuls eines Elementarteilchens.
Beitrag 1981-68
-
Die Krümmung der Raumzeit ist eine Funktion des Energie-Impuls-Tensors. Das ist etwas völlig anderes als der Impuls eines Elementarteilchen.
Auf diesem Niveau ist eine Diskussion sinnlos. Wir müssen an die Basics ran oder die Sache sein lassen.
Grüße
zara.t.�
Grtgrt aus 1981-63:Was die Raumzeit krümmt, sind letztlich jene Energie-Impulse (und das ohne Rücksicht darauf, was sie verursacht hat). Unter einem elementaren Energie-Impuls verstehe ich den Impuls eines Elementarteilchens.
Die Krümmung der Raumzeit ist eine Funktion des Energie-Impuls-Tensors. Das ist etwas völlig anderes als der Impuls eines Elementarteilchen.
Auf diesem Niveau ist eine Diskussion sinnlos. Wir müssen an die Basics ran oder die Sache sein lassen.
Grüße
zara.t.�
Beitrag 1981-9
Einsteins Definition von Gleichzeitigkeit
Hallo Grtgrt,
in der Relativitätstheorie gibt es einen wohldefinierten Begriff der Gleichzeitigkeit, nämlich die Einsteinsche Gleichzeitigkeitsdefinition.
Nach Albert Einstein kann man kann die Gleichzeitigkeit entfernter Ereignisse nicht erkennen, sondern nur definieren. Diese Definition ist willkürlich: man kann irgendeine Festsetzung darüber treffen, ohne dass ein Fehler entsteht.
Nach der Einsteinschen Gleichzeitigkeitsdefinition gelten zwei Ereignisse an verschiedenen Orten A und B als gleichzeitig, wenn ein auf dem Mittelpunkt M der Verbindungsgeraden platzierter Beobachter Lichtsignale von beiden Ereignissen gleichzeitig bei sich eintreffen sieht.
Dass das Licht zum Durchlaufen des Weges A -> M und zum Durchlaufen der Strecke B -> M dieselbe Zeit brauche, ist keine Voraussetzung oder Hypothese über die physikalische Natur des Lichtes, sondern eine Festsetzung, die man nach freiem Ermessen treffen kann, um zu einer Definition der Gleichzeitigkeit zu gelangen.
M.f.G. Eugen Bauhof�
Grtgrt aus 1981-4:Als was also soll der Abstand der beiden dann definiert sein? Als der zu Beginn der Messung oder als der zu Ende der Messung? Oder als Durchschnitt davon?
Und können sich Beobachter und Planet denn überhaupt auf einen gemeinsamen Zeitpunkt "Beginn der Messung" verständigen, wo wir doch wissen, dass es einen wohldefinierten Begriff "gleichzeitig" nach der ART gar nicht geben kann?
Hallo Grtgrt,
in der Relativitätstheorie gibt es einen wohldefinierten Begriff der Gleichzeitigkeit, nämlich die Einsteinsche Gleichzeitigkeitsdefinition.
Nach Albert Einstein kann man kann die Gleichzeitigkeit entfernter Ereignisse nicht erkennen, sondern nur definieren. Diese Definition ist willkürlich: man kann irgendeine Festsetzung darüber treffen, ohne dass ein Fehler entsteht.
Nach der Einsteinschen Gleichzeitigkeitsdefinition gelten zwei Ereignisse an verschiedenen Orten A und B als gleichzeitig, wenn ein auf dem Mittelpunkt M der Verbindungsgeraden platzierter Beobachter Lichtsignale von beiden Ereignissen gleichzeitig bei sich eintreffen sieht.
Dass das Licht zum Durchlaufen des Weges A -> M und zum Durchlaufen der Strecke B -> M dieselbe Zeit brauche, ist keine Voraussetzung oder Hypothese über die physikalische Natur des Lichtes, sondern eine Festsetzung, die man nach freiem Ermessen treffen kann, um zu einer Definition der Gleichzeitigkeit zu gelangen.
M.f.G. Eugen Bauhof�
Beitrag 1981-10
Warum Einsteins Definition wenig nützt
Hallo Eugen,
danke für den Hinweis. Und tatsächlich:
Auf den ersten Blick schien mir Einsteins Definition von Gleichzeitigkeit recht sinnvoll.
Bei genaueren Hinsehen aber erkenne ich sie als zu wenig nützlich. Das liegt daran, dass es im konkreten Fall ja gar nicht so einfach ist zu sehen, wo der Mittelpunkt zwischen zwei Orten A und B denn nun genau liegt.
Mit anderen Worten: Sich einfach eine A und B verbindende gerade Strecke vorzustellen, deren Mittelpunkt man als genau definiert sehen könnte, geht nicht.
Sinn machen kann Einsteins Definition also höchstens im Kontext der für viele Anwendungen zu ungenauen Speziellen Relativitätstheorie (oder wo A und B nicht besonders weit voneinander entfernt sind).
Gruß, grtgrt
Hallo Eugen,
danke für den Hinweis. Und tatsächlich:
Auf den ersten Blick schien mir Einsteins Definition von Gleichzeitigkeit recht sinnvoll.
Bei genaueren Hinsehen aber erkenne ich sie als zu wenig nützlich. Das liegt daran, dass es im konkreten Fall ja gar nicht so einfach ist zu sehen, wo der Mittelpunkt zwischen zwei Orten A und B denn nun genau liegt.
- Er ist nämlich selbst zeitabhängig (da A und B sich ja i.A. relativ zueinander bewegen),
- und selbst die A und B verbindende Geodäte der Raumzeit ist ständigem Wandel unterworfen (z.B. ganz gravierend dann, wenn ein großer Stern gerade im Begriff ist, irgendwo in ihrer Nähe vorbeizuziehen).
Mit anderen Worten: Sich einfach eine A und B verbindende gerade Strecke vorzustellen, deren Mittelpunkt man als genau definiert sehen könnte, geht nicht.
Sinn machen kann Einsteins Definition also höchstens im Kontext der für viele Anwendungen zu ungenauen Speziellen Relativitätstheorie (oder wo A und B nicht besonders weit voneinander entfernt sind).
Gruß, grtgrt
Beitrag 1981-16
Was nicht beobachtbar ist, existiert auch nicht (Bohrs Prinzip)
Hi Henry,
mir kommt es darauf an, hier bestätigt zu sehen, dass ich in der Sache einer Meinung mit Einstein zu sein scheine.
Gruß, grtgrt
Bauhof aus 1981-9:
Nach Albert Einstein kann man kann die Gleichzeitigkeit entfernter Ereignisse nicht erkennen, ...
Hi Henry,
mir kommt es darauf an, hier bestätigt zu sehen, dass ich in der Sache einer Meinung mit Einstein zu sein scheine.
Gruß, grtgrt
Beitrag 1981-81
Freier Fall im Sinne der Allgemeinen Relativitätstheorie
Hi Okotombrok,
im Prinzip bin ich da deiner Meinung. Und deswegen ist mir klar, dass hier ganz sicher keine Fliehkraft mehr wirkt.
Dass sich Erde und Satellit aber auch nicht mehr per Gravitationskraft anziehen sollten, finde ich schwer einzusehen. Frage also:
Muss so ein Satellit, wenn man will, dass er die gewünschte Umlaufbahn wirklich über Jahrtausende hinweg einhält, nicht doch hin und wieder ein klein wenig beschleunigt werden?
Gruß, grtgrt
Okotombrok aus 1981-78:
Der Satellit befindet sich nun im freien Fall um die Erdkugel herum.
Da braucht es keine Flieh- oder Gravitationskräfte, die daran zerren und auch die Insassen können nicht unterscheiden, ob sie im intergalaktischen Raum fernab jeglicher Massen schweben, sich in einem frei fallenden Fahrstuhl befinden oder vom Dach fallen.
Sie können es nicht weil es ununterscheidbar ist.
Es geht letztendlich um die Metrik der Raumzeit und nicht um Kräfte.
Hi Okotombrok,
im Prinzip bin ich da deiner Meinung. Und deswegen ist mir klar, dass hier ganz sicher keine Fliehkraft mehr wirkt.
Dass sich Erde und Satellit aber auch nicht mehr per Gravitationskraft anziehen sollten, finde ich schwer einzusehen. Frage also:
Muss so ein Satellit, wenn man will, dass er die gewünschte Umlaufbahn wirklich über Jahrtausende hinweg einhält, nicht doch hin und wieder ein klein wenig beschleunigt werden?
Gruß, grtgrt
Beitrag 1981-82
-
Guten Morgen,
wenn man die Bahnkurve als Resultierende aus Fliehkraft und Schwerkraft beschreibt, ist man in der Newtonschen Physik und nicht in der ART. In der ART ist es so wie zB Okotombrok es beschrieben hat. man darf die Theorien nicht durcheinanderwirbeln.
Ob ich die Zeit habe für die Basics weiß ich nicht. Eher nicht. Aber da gibt es doch im Netz schon sehr gut aufbereitetes Material. Auch Eugen Bauhof hat da schon Vorarbeit geleistet. Schaun mer mal. SRT dürfte auch noch einigermaßen machbar sein. ART geht hier im Forum nur ohne Mathematik. Die dazugehörige Differentialgeometrie ist zu anspruchsvoll.
Aber schaun mer mal. :-)
Melde mich demnächst ausführlicher zum Thema.
zara.t.�
wenn man die Bahnkurve als Resultierende aus Fliehkraft und Schwerkraft beschreibt, ist man in der Newtonschen Physik und nicht in der ART. In der ART ist es so wie zB Okotombrok es beschrieben hat. man darf die Theorien nicht durcheinanderwirbeln.
Ob ich die Zeit habe für die Basics weiß ich nicht. Eher nicht. Aber da gibt es doch im Netz schon sehr gut aufbereitetes Material. Auch Eugen Bauhof hat da schon Vorarbeit geleistet. Schaun mer mal. SRT dürfte auch noch einigermaßen machbar sein. ART geht hier im Forum nur ohne Mathematik. Die dazugehörige Differentialgeometrie ist zu anspruchsvoll.
Aber schaun mer mal. :-)
Melde mich demnächst ausführlicher zum Thema.
zara.t.�
Beitrag 1981-83
-
Hi Zara,
danke für deinen Hinweis — er zeigt mir, dass meine Frage an Okotombrok wirklich dumm war.
Denn dass die Geodäte, auf der der Satellit sich im freien Fall befindet, nicht durch die Erde führt, hatte ich ja schon aus der Tatsache folgern können, dass die Bahn der Planeten um die Sonne nicht ständig enger wird.
Nebenbei:
Ich wundere mich nun schon Jahrzehnte lang darüber, dass physikalische Zusammenhänge sich i.a.R. über sehr einfache mathematische Formeln beschreiben lassen.
Erst seitdem ich hier im Zeitforum mit euch diskutiere, fällt mir auf, wie gut verständlich komplizierte Physik auch über rein umgangssprachliche Mittel beschreibbar ist (natürlich nur qualitativ — aber immerhin so, dass man gut zu verstehen glaubt, wie denn da so alles zusammenhängt und zusammenwirkt).
Bin gespannt, ob sich auch Natur und Zweck des Energie-Impuls-Tensors rein qualitativ so gut beschreiben lassen.
Bis dann,
mit besten Grüßen,
grtgrt
Hi Zara,
danke für deinen Hinweis — er zeigt mir, dass meine Frage an Okotombrok wirklich dumm war.
Denn dass die Geodäte, auf der der Satellit sich im freien Fall befindet, nicht durch die Erde führt, hatte ich ja schon aus der Tatsache folgern können, dass die Bahn der Planeten um die Sonne nicht ständig enger wird.
Nebenbei:
Ich wundere mich nun schon Jahrzehnte lang darüber, dass physikalische Zusammenhänge sich i.a.R. über sehr einfache mathematische Formeln beschreiben lassen.
Erst seitdem ich hier im Zeitforum mit euch diskutiere, fällt mir auf, wie gut verständlich komplizierte Physik auch über rein umgangssprachliche Mittel beschreibbar ist (natürlich nur qualitativ — aber immerhin so, dass man gut zu verstehen glaubt, wie denn da so alles zusammenhängt und zusammenwirkt).
Bin gespannt, ob sich auch Natur und Zweck des Energie-Impuls-Tensors rein qualitativ so gut beschreiben lassen.
Bis dann,
mit besten Grüßen,
grtgrt
Beitrag 2058-16
Ursache der Relativität von Zeit und Raum
Wie kommst Du auf die Idee, dass räumliche und zeitliche Abstände in der ART nicht ebenso relativ sein sollen wie in der SRT?
Meiner Ansicht nach besteht der Unterschied beider Theorien in dieser Hinsicht nur darin, dass
Die Relativität von Zeit und Raum (d.h. die relative Wahrnehmung der Länge von örtlichen oder zeitlichen Abständen) geht einzig und alleine zurück auf die beiden Axiome:
Nicht mal die Konstanz der Lichtgeschwindigkeit ist für Relativität notwendig. Dass sie tatsächlich gegeben ist, vereinfacht die Rechnungen natürlich erheblich.
Gruß, grtgrt
Henry in 2058-13:
Und Raum und Zeit sind relativ? Es geht doch um die Raumzeit als Gesamtheit, und die ist nicht relativ.
Wie kommst Du auf die Idee, dass räumliche und zeitliche Abstände in der ART nicht ebenso relativ sein sollen wie in der SRT?
Meiner Ansicht nach besteht der Unterschied beider Theorien in dieser Hinsicht nur darin, dass
- unbeschleunigte Bewegung im Minkowski-Raum stets eine geradlinige Bewegung ist,
- wohingegen sie in der Raumzeit entlang einer (gekrümmten) Geodäte vor sich geht — und deswegen weit schwieriger zu beschreiben ist.
Die Relativität von Zeit und Raum (d.h. die relative Wahrnehmung der Länge von örtlichen oder zeitlichen Abständen) geht einzig und alleine zurück auf die beiden Axiome:
- Die Lichtgeschwindigkeit ist endlich und
- Information über eingetretene Ereignisse breitet sich grundsätzlich mit Lichtgeschwindigkeit aus.
Nicht mal die Konstanz der Lichtgeschwindigkeit ist für Relativität notwendig. Dass sie tatsächlich gegeben ist, vereinfacht die Rechnungen natürlich erheblich.
Gruß, grtgrt
Beitrag 1997-80
Erst unterschiedlich beschleunigt zu werden gibt Zwillingen unterschiedliches Alter (?)
Beschleunigung — und wirklich nur sie — dehnt Eigenzeit
Hallo Henry,
diese Aussage Müllers ist richtig — aber eben n u r wegen der Vergröberung, mit der sie formuliert ist. Diese Vergröberung (ein Ausblenden wirklich wichtiger Details) besteht darin, dass diese Formulierung den qualitativen Unterschied zwischen der Raumzeit einerseits und beobachterspezifischen S i c h t e n darauf andererseits völlig ignoriert.
Tatsache ist:
Eine Dilation der Zeit und zu ihr korrelierte Kontraktion von Längen gibt es NUR im Sinne der S i c h t e n ,
aber keineswegs im Sinne der Struktur der Raumzeit (der SRT) selbst.
Dass dem wirklich so ist, erkennt man sehr schön, wenn man sich zwei Personen X und Y vorstellt, die sich mit gleichförmiger Geschwindigkeit zuerst voneinander entfernen um dann, wenn jeder den jeweils anderen in einer Entfernung von genau 100 km vermutet, mit eben derselben Geschwindigkeit wieder aufeinander zuzufliegen.
Bitte beachte:
Wir sehen also: Das Zwillingsparadoxon gibt es n u r in der Raumzeit der ART, aber n i c h t in der Raumzeit der SRT.
In der SRT sind beobachtete Unterschiede wirklich n u r darauf zurückzuführen, dass Beobachter, die solche Unterschiede feststellen, aus unterschiedlichen Bezugssystemen heraus argumentieren.
In der ART dageben kommt unterschiedliches Altern der Zwillinge durchaus zustande, da hier auch die für beide Personen unterschiedlichen Beschleunigungen mit berücksichtigt werden: eine Art von Kraftwirkung also, die die SRT gar nicht erst zu betrachten versucht.
Gruß,
grtgrt
PS: Eine erweiterte, über Einstein hinausgehende Form der SRT löst das Zwillingsparadoxon dennoch. Genauer:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch Aussagen darüber machen kann, wie sich Beschleunigung auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche Ergebnisse tatsächlich mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrundeliegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
ausschließlich auf jene Phasen der Reise zurückführt, in denen die beiden Zwillinge unterschiedlich beschleunigt waren.
FAZIT also:
Henry in 1997-67:
Um nicht immer aus Wikipedia zu zitieren:
» Durch Einstein wurde unser Verständnis von Raum und Zeit radikal neu gestaltet: Phänomene wie Zeitdilatation und Lorentz-Kontraktion und die Verschmelzung von Raum und Zeit im Raum-Zeit-Kontinuum sind eine natürliche Konsequenz der Speziellen Relativitätstheorie. «
Ein Zitat aus http://www.wissenschaft-online.de/astrowissen/ von Dr. Andreas Müller.
Der Autor Dr. Andreas Müller ist Astrophysiker und wissenschaftlicher Koordinator im Exzellenzcluster "Origin and Structure of the Universe" der Technischen Universität München.
Hallo Henry,
diese Aussage Müllers ist richtig — aber eben n u r wegen der Vergröberung, mit der sie formuliert ist. Diese Vergröberung (ein Ausblenden wirklich wichtiger Details) besteht darin, dass diese Formulierung den qualitativen Unterschied zwischen der Raumzeit einerseits und beobachterspezifischen S i c h t e n darauf andererseits völlig ignoriert.
Tatsache ist:
aber keineswegs im Sinne der Struktur der Raumzeit (der SRT) selbst.
Dass dem wirklich so ist, erkennt man sehr schön, wenn man sich zwei Personen X und Y vorstellt, die sich mit gleichförmiger Geschwindigkeit zuerst voneinander entfernen um dann, wenn jeder den jeweils anderen in einer Entfernung von genau 100 km vermutet, mit eben derselben Geschwindigkeit wieder aufeinander zuzufliegen.
Bitte beachte:
- Dies ist ein absolut symmetrisches Szenario.
- Aus Sicht der einen Person geht die Uhr der jeweils anderen langsamer,
- und doch werden beide Uhren — wenn die beiden Personen sich wieder treffen — genau gleiche Zeit anzeigen (das folgt aus der Symmetrie des Szenarios und ist deswegen so, weil X und Y dann ja auch wieder dasselbe Bezugssystem haben).
Wir sehen also: Das Zwillingsparadoxon gibt es n u r in der Raumzeit der ART, aber n i c h t in der Raumzeit der SRT.
In der SRT sind beobachtete Unterschiede wirklich n u r darauf zurückzuführen, dass Beobachter, die solche Unterschiede feststellen, aus unterschiedlichen Bezugssystemen heraus argumentieren.
In der ART dageben kommt unterschiedliches Altern der Zwillinge durchaus zustande, da hier auch die für beide Personen unterschiedlichen Beschleunigungen mit berücksichtigt werden: eine Art von Kraftwirkung also, die die SRT gar nicht erst zu betrachten versucht.
Gruß,
grtgrt
PS: Eine erweiterte, über Einstein hinausgehende Form der SRT löst das Zwillingsparadoxon dennoch. Genauer:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch Aussagen darüber machen kann, wie sich Beschleunigung auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche Ergebnisse tatsächlich mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrundeliegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
FAZIT also:
- Wer von der SRT (in Einsteins Fassung) ausgeht, geht von einer Theorie aus, die zu beschleunigten Bewegungen nichts aussagen will und demnach auf die Situation des Zwillingsparadoxon gar nicht anwendbar ist.
- Seit etwa 2000 aber geht man nicht mehr davon aus, dass die SRT — wenn man versucht, sie auch auf beschleunigte Bewegung anzuwenden — falsche Aussagen macht. Soweit man nämlich Beispiele in SRT u n d ART durchgerechnet hat, kam man zum gleichen Ergebnis (was aber nicht heißt, dass wirklich alles, was die ART sagt, auch mit Mitteln der SRT nachrechenbar wäre).
- Es kommt hier wohl die Tatsache zum Tragen, dass in jeder hinreichend kleinen Umgebung eines nicht singulären Punktes P der Raumzeit der ART die SRT sehr gute Approximation der ART ist.
tags: SRT1gegreit Einstein1gegreit Beobachter1gegreit
 Nach oben
Nach oben