Beitrag 0-340
Wie sich der Begriff » Unser Universum « definiert
Wie sich » Unser Universum « definiert
Noch im 20. Jahrhundert verstand man unter dem Universum
Inzwischen aber hat der Wortgebrauch sich gewandelt. Heute wird
Die Grenze unseres Universums — man nennt sie unseren Horizont — ist der Teil der Raumzeit, der von der Erde aus — prinzipiell jedenfalls — einsehbar ist.
Wie sich beide genau unterscheiden, findet sich erklärt in Notiz » Wie sich Beobachtungs- und Ereignishorizont unterscheiden «.
Lies auch: Warum wir tatsächlich in einem Multiversum leben.
Kurz gesagt: Unser Universum ist der durch uns wahrnehmbare Teil des Weltalls (genauer: der Raumzeit). Da sich jedem Objekt im Weltall sein eigenes Universum zuordnet, sprechen Physiker neuerdings vom Multiversum.
Noch im 20. Jahrhundert verstand man unter dem Universum
- als Physiker oder Astronom das gesamte Weltall,
- als Philosoph aber den gesamten Kosmos (= die philosophische Interpretation des Weltalls und all seiner Inhalte).
Inzwischen aber hat der Wortgebrauch sich gewandelt. Heute wird
- das gesamte Weltall als Multiversum bezeichnet,
- und wer weiter vom Universum spricht, meint damit meist einfach nur noch unser Universum ( in dessen Mittelpunkt die Erde sitzt ).
Die Grenze unseres Universums — man nennt sie unseren Horizont — ist der Teil der Raumzeit, der von der Erde aus — prinzipiell jedenfalls — einsehbar ist.
- In zeitlicher Hinsicht gesehen, ist damit unser Beobachtungshorizont gemeint. Die kosmische Hintergrundstrahlung zeigt uns, wie er aussieht (er hat also tatächlich ein Aussehen).
- In räumlicher Hinsicht aber ist unser Horizont das, was man unseren Ereignishorizont nennt.
Wie sich beide genau unterscheiden, findet sich erklärt in Notiz » Wie sich Beobachtungs- und Ereignishorizont unterscheiden «.
Lies auch: Warum wir tatsächlich in einem Multiversum leben.
Kurz gesagt: Unser Universum ist der durch uns wahrnehmbare Teil des Weltalls (genauer: der Raumzeit). Da sich jedem Objekt im Weltall sein eigenes Universum zuordnet, sprechen Physiker neuerdings vom Multiversum.
Beitrag 0-321
Wie sich Beobachtungs- und Ereignishorizont unterscheiden
Wie sich Beobachtungs- und Ereignishorizont unterscheiden
Ist A das Alter unseres Universums — d.h. die Zahl der seit dem Urknall vergangenen Jahre — so wird der Radius des durch Menschen einsehbaren Teil des Universums stets A - 380 000 Lichtjahre betragen: Es ist dies die Zeit, welche die kosmische Hintergrundstrahlung benötigt, uns zu erreichen. Sie nämlich stellt sich uns dar wie eine Nebelwand, hinter die wir nicht mehr weiter in die Vergangenheit sehen können.
Man nennt diesen Radius unseren Beobachtungshorizont. Er wird nur bestimmt durch das Alter unseres Universums.
Ganz anders unser Ereignishorizont: Er ist zusätzlich noch davon abhängig, mit welcher Rate der Raum expandiert (oder irgendwann vielleicht auch mal schrumpfen könnte). Dieser Horizont ist gegeben durch alle Punkte im All, die sich von uns mit exakt Lichtgeschwindigkeit entfernen. Das Licht von Galaxien, die jenseits davon liegen, wird unsere Milchstraße — immer unter der Voraussetzung, dass der Raum niemals mehr schrumpfen wird — nie mehr erreichen.
Insgesamt also gilt:
Man kann es auch so sagen:
Solange unser Ereignishorizont schrumpft, muss man davon ausgehen, dass unsere Welt in einem sog. Big Whimper enden wird, was bedeutet, dass die Materiekonzentration in unserem Universum ständig nur schrumpfen wird bis schließlich sogar alle Schwarzen Löcher verdampft sein werden.
Insbesondere wird dann an Materie gebundenes intelligentes Leben in dem Bereich des Kosmos, der heute unser Universum darstellt, NICHT MEHR MÖGLICH sein.
Wie schon in den frühen 1920-er Jahren Alexander Friedmann erkannt hat, bestimmt die Rate, mit der die Expansionsgeschwindigkeit des Raumes sich über die Zeit hinweg verändert, die Geometrie der Raumzeit:
Regionen in diesem Sinne sind sehr viel größer als unser beobachtbares Universum: Sie sind sozusagen eigene Universen. Kein Wunder also, dass uns Menschen die Raumzeit um uns herum als kaum gekrümmt, d.h. als flach erscheint.
Ist A das Alter unseres Universums — d.h. die Zahl der seit dem Urknall vergangenen Jahre — so wird der Radius des durch Menschen einsehbaren Teil des Universums stets A - 380 000 Lichtjahre betragen: Es ist dies die Zeit, welche die kosmische Hintergrundstrahlung benötigt, uns zu erreichen. Sie nämlich stellt sich uns dar wie eine Nebelwand, hinter die wir nicht mehr weiter in die Vergangenheit sehen können.
Man nennt diesen Radius unseren Beobachtungshorizont. Er wird nur bestimmt durch das Alter unseres Universums.
Ganz anders unser Ereignishorizont: Er ist zusätzlich noch davon abhängig, mit welcher Rate der Raum expandiert (oder irgendwann vielleicht auch mal schrumpfen könnte). Dieser Horizont ist gegeben durch alle Punkte im All, die sich von uns mit exakt Lichtgeschwindigkeit entfernen. Das Licht von Galaxien, die jenseits davon liegen, wird unsere Milchstraße — immer unter der Voraussetzung, dass der Raum niemals mehr schrumpfen wird — nie mehr erreichen.
Insgesamt also gilt:
- Unser Beobachtungshorizont — eine z e i t l i c h e Distanz — ist ständig im Wachsen begriffen,
- unser Ereignishorizont aber — eine r ä u m l i c h e Distanz — schrumpft, solange der Raum expandiert.
In etwa 100 Milliarden Jahren — so hat Brian Greene errechnet — werden sich innerhalb unseres Ereignishorizonts nur noch Galaxien der sog. Lokalen Gruppe befinden: zwischen 30 und 50 Galaxien, die heute sämlich sehr nahe Nachbarn der Milchstraße sind.
Man kann es auch so sagen:
- Unser Beobachtungshorizont quantifiziert die das Alter unseres Universums,
- unser Ereignishorizont aber quantifiziert seine räumliche Ausdehnung und seine Reichhaltigkeit, d.h. die Menge von Objekten, mit denen wir kommunizieren können.
Solange unser Ereignishorizont schrumpft, muss man davon ausgehen, dass unsere Welt in einem sog. Big Whimper enden wird, was bedeutet, dass die Materiekonzentration in unserem Universum ständig nur schrumpfen wird bis schließlich sogar alle Schwarzen Löcher verdampft sein werden.
Insbesondere wird dann an Materie gebundenes intelligentes Leben in dem Bereich des Kosmos, der heute unser Universum darstellt, NICHT MEHR MÖGLICH sein.
Wie schon in den frühen 1920-er Jahren Alexander Friedmann erkannt hat, bestimmt die Rate, mit der die Expansionsgeschwindigkeit des Raumes sich über die Zeit hinweg verändert, die Geometrie der Raumzeit:
- In Regionen, in denen der Raum zunehmend schneller expandiert — sein Inhalt sich dann also immer mehr verdünnt —, ist die Raumzeit negativ (hyperbolisch) gekrümmt, d.h. Dreiecke haben dort eine Winkelsumme, die kleiner als 180 Grad ist.
- In Regionen aber, in denen die Expansion abflaut — und so das Universum auf einen Big Crunch zusteuert —, ist die Raumzeit positiv (elliptisch) gekrümmt, d.h. Dreiecke haben dort eine Winkelsumme, die größer als 180 Grad ist.
Regionen in diesem Sinne sind sehr viel größer als unser beobachtbares Universum: Sie sind sozusagen eigene Universen. Kein Wunder also, dass uns Menschen die Raumzeit um uns herum als kaum gekrümmt, d.h. als flach erscheint.
Beitrag 0-346
Zwei Experimente zum Beweis der Nichlokalität von Quanten
John Wheeler's Experiment verzögerter Entscheidung
Wie Quanten den Raum durchfließen zeigt sich besonders eindrucksvoll in einem Experiment, das John Wheeler 1981 vorschlug (das aber erst 2006 auch tatsächlich durchgeführt wurde):
Ein Photon trifft auf einen Strahlteiler und läuft dann über die beiden so entstehenden Wege hin zu Detektoren an den Enden der beiden Wege. Man kann nun — direkt vor den Detektoren, am Schittpunkt beider Wege, einen zweiten Strahlteiler einbauen, und das erst, nachdem das Photon schon unterwegs ist (das ist die verzögerte Entscheidung).
Da Licht stets nur mit endlicher Geschwindigkeit unterwegs ist, kann keine Information schon wenn das Photon den ersten Strahlteiler erreicht, zum zweiten Strahlteiler gelangt sein.
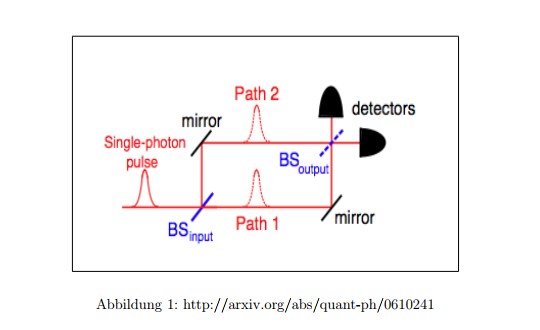
Entscheidet man sich nach diesem Zeitpunkt zum Einbau des zweiten Strahlteilers, so ergeben sich — wenn die Länge beider Wege sich um die halbe Wellenlänge des Photons unterscheiden — in den Detektoren Interferenzerscheinungen. Sie beweisen: Das Photon floss über beide Wege.
Wird der Zweite Strahlteiler nicht eingebaut, spricht einfach nur — mit jeweils 50%-iger Wahrscheinlichkeit — der eine oder der andere Detektor an. Zu Interferenz aber kommt es nicht. Es sieht dann also so aus, als wäre das Photon nur über einen der beiden Wege gekommen.
Wann also, so frägt man sich als Vertreter der klassischen Physik, entscheidet sich das Photon, welchen Weg es nehmen will?
Die Antwort ist: Es braucht sich nicht zu entscheiden, denn als Welle nimmt es stets beide Wege, und so ist am Experiment überhaupt nichts Paradoxes.
Merkwürdigkeiten entstehen nur für den, der denkt, das Photon könne (wie ein Kügelchen) nur einen der beiden Wege nehmen. Tatsächlich aber breitet es sich stets über beide Wege aus, und der zweite Strahlteiler sorgt dafür, dass die über den einen Weg kommende Teilwelle mit der über den anderen Weg kommenden interferiert (was sie ohne den zweiten Strahlteiler nicht tun kann).
Hinweis:
Natürlich beweist auch schon das Doppelspalt-Experiment die Nichtlokalität von Quanten. Wer nämlich sog. "Weginformation" besorgen möchte, stellt hinter die Spalten Polarisatoren, um die beiden Teilwellen, in die zwei Spalten ein auf sie zukommendes Photon zerlegen, senkrecht zueinander zu polarisieren (damit sie unterscheidbar werden) — senkrecht zueinander polarisierte Wellen aber können nicht interferieren. Eben deswegen verschwindet die Interferenz genau dann, wenn versucht wird, Weginformation zu erhalten.
Wie Quanten den Raum durchfließen zeigt sich besonders eindrucksvoll in einem Experiment, das John Wheeler 1981 vorschlug (das aber erst 2006 auch tatsächlich durchgeführt wurde):
Ein Photon trifft auf einen Strahlteiler und läuft dann über die beiden so entstehenden Wege hin zu Detektoren an den Enden der beiden Wege. Man kann nun — direkt vor den Detektoren, am Schittpunkt beider Wege, einen zweiten Strahlteiler einbauen, und das erst, nachdem das Photon schon unterwegs ist (das ist die verzögerte Entscheidung).
Da Licht stets nur mit endlicher Geschwindigkeit unterwegs ist, kann keine Information schon wenn das Photon den ersten Strahlteiler erreicht, zum zweiten Strahlteiler gelangt sein.

Entscheidet man sich nach diesem Zeitpunkt zum Einbau des zweiten Strahlteilers, so ergeben sich — wenn die Länge beider Wege sich um die halbe Wellenlänge des Photons unterscheiden — in den Detektoren Interferenzerscheinungen. Sie beweisen: Das Photon floss über beide Wege.
Wird der Zweite Strahlteiler nicht eingebaut, spricht einfach nur — mit jeweils 50%-iger Wahrscheinlichkeit — der eine oder der andere Detektor an. Zu Interferenz aber kommt es nicht. Es sieht dann also so aus, als wäre das Photon nur über einen der beiden Wege gekommen.
Wann also, so frägt man sich als Vertreter der klassischen Physik, entscheidet sich das Photon, welchen Weg es nehmen will?
Die Antwort ist: Es braucht sich nicht zu entscheiden, denn als Welle nimmt es stets beide Wege, und so ist am Experiment überhaupt nichts Paradoxes.
Merkwürdigkeiten entstehen nur für den, der denkt, das Photon könne (wie ein Kügelchen) nur einen der beiden Wege nehmen. Tatsächlich aber breitet es sich stets über beide Wege aus, und der zweite Strahlteiler sorgt dafür, dass die über den einen Weg kommende Teilwelle mit der über den anderen Weg kommenden interferiert (was sie ohne den zweiten Strahlteiler nicht tun kann).
Hinweis:
Natürlich beweist auch schon das Doppelspalt-Experiment die Nichtlokalität von Quanten. Wer nämlich sog. "Weginformation" besorgen möchte, stellt hinter die Spalten Polarisatoren, um die beiden Teilwellen, in die zwei Spalten ein auf sie zukommendes Photon zerlegen, senkrecht zueinander zu polarisieren (damit sie unterscheidbar werden) — senkrecht zueinander polarisierte Wellen aber können nicht interferieren. Eben deswegen verschwindet die Interferenz genau dann, wenn versucht wird, Weginformation zu erhalten.
Beitrag 0-349
Der Unruh-Effekt — Wie sich Quantenfluktuation aus Sicht eines im Minkowski-Vakuum beschleinigten Beobachters als Wärmebad darstellt
Der Unruh-Effekt zeigt:
Das Vakuum ist nicht leer, sondern nur Zustand kleinster (Quantenfeld-) Energie
Claus Kiefer beschreibt auch, wie dieser Effekt zustande kommt. Seine Erklärung verstehe ich zu wenig, um sie hier wiedergeben zu können. Sie scheint mir ähnlich der 2017 in arXiv publizierten.
Auf eine wichtige Schlussfolgerung wird am Ende der kurzen Rechnung » The Unruh Effect « hingewiesen. Man liest dort:
Das Vakuum ist nicht leer, sondern nur Zustand kleinster (Quantenfeld-) Energie
Claus Kiefer ( auf S. 127 in Quantenkosmos ):
Ein Beobachter, der sich auf gerader Linie mit konstanter Beschleunigung durchs Minkowski-Vakuum bewegt, erlebt dieses Vakuum, als sei es mit Teilchen gefüllt: Seine Detektoren werden entsprechend angeregt. Die Verteilung dieser scheinbar vorhandenen Teilchen ist nicht beliebig. Sie entspricht einem Wärmebad mit bestimmter Temperatur, welche proportional zum Produkt aus Beschleunigung und Planckschem Wirkungsquantum ist.
Ein rohes Ei würde demnach — wenn extrem stark beschleunigt — gekocht werden.
Erstmals beschrieben hat diesen Effekt 1976 der amerikanische Physiker William Unruh.
Claus Kiefer beschreibt auch, wie dieser Effekt zustande kommt. Seine Erklärung verstehe ich zu wenig, um sie hier wiedergeben zu können. Sie scheint mir ähnlich der 2017 in arXiv publizierten.
Auf eine wichtige Schlussfolgerung wird am Ende der kurzen Rechnung » The Unruh Effect « hingewiesen. Man liest dort:
-
The Unruh effect shows that the vacuum in quantum field theory is essentially thermal.
It should also make you think about what do we really mean by the vacuum: If we interpret the vacuum as “the nothing state”, then the Unruh effect seems very odd indeed, and there seems to be no physical explanation for it. The proper explanation for the vacuum state is thus » the state of lowest energy « – from this angle, the Unruh effect does not seem so strange anymore, since accelerating observes feel “forces” which will make them interpret the state of lowest energy differently.
Beitrag 0-350
Der durch Quantenfluktuation getriebene Dekohärenzprozess generiert, was wir als » Zeit « bezeichnen
Dekohärenz generiert den quantenphysikalischen Zeitpfeil
Da Dekohärenz die klassischen Eigenschaften makroskopischer Objekte generiert, ist unser gewöhnlicher Zeitpfeil ein aus dem quantenmechanischen Zeitpfeil emergierender. Klar wird:
Was wir als » Zeit « begreifen, ist nichts anderes als ein Prozess laufender Zustandsveränderung.
Claus Kiefer ( S. 156-157 in Quantenkosmos ):
Quantenverschränkung — ein ganz wesentlicher Aspekt der Quantentheorie — zeigt uns, dass Beobachter — da sie ja stets nur lokal beobachten, die Welt verschränkter Quanten aber nichtlokal ist — niemals alle Information über einen Quantenzustand haben können.
Jedem Beobachter, der von zwei verschränkten Teilchen nur eines befragen kann, fehlt Information, weswegen das beobachtete Teilchen für ihn Entropie hat (Entropie quantifiziert fehlende Information).
Keine Entropie gäbe es nur, wenn wir die Wellenfunktion des gesamten Universums kennen würden.
Da der ständig gegebene Dekohärenz-Prozess jedes Teilchen aber mit ständig noch mehr anderen Teilchen verschränkt, wird jene Entropie ständig zunehmen.
Wir sehen:
Auch die quantenmechanische Entropie gehorcht dem 2. Hauptsatz der Thermodynamik,
und der sich daraus ergebende quantenmechanische Zeitpfeil ist eng mit dem Prozess der Dekohärenz verbunden.
Da Dekohärenz die klassischen Eigenschaften makroskopischer Objekte generiert, ist unser gewöhnlicher Zeitpfeil ein aus dem quantenmechanischen Zeitpfeil emergierender. Klar wird:
Beitrag 0-352
Hintergrundunabhänge Theorien sind nur ART und Quantengravitation.
Von SRT über ART zu einer Quantengravitationstheorie
Claus Kiefer (auf S. 232 in Quantenkosmos ):
In den nicht-gravitativen Theorien — beispielsweise der SRT — sind Felder immer auf einer nicht-dynamischen Raumzeit definiert.
Ganz anders in Einsteins ART: Dort ist die Geometrie der Raumzeit identisch mit der Form des Gravitationsfeldes — also selbst dynamisch.
Schon Einstein bereitete das Kopfzerbrechen. So verzögerte sich die Aufstellung seiner Theorie um 2 Jahre, weil er zunächst noch am Glauben festhielt, dass den Punkten einer Raumzeit (gemeint sind Punkte im mathematischen Sinne) eine vom Gravitationsfeld unabhängige Bedeutung zukomme.
Für Mathematiker mag das sinnvoll sein, für einen Physiker aber nicht: Das durch die Geometrie der Raumzeit gegebene Gravitationsfeld ist wirklich schon alles. Und so sind bei einer Koordinatentransformation Punkte, Metrik und Materiefelder gleichermaßen zu transformieren.
Erst nachdem Einstein das erkannt hatte, kam er 1915 zu den korrekten Feldgleichungen der Gravitation.
Für die Entwicklung einer Quantengravitationstheorie ist dieser Punkt von großer Wichtigkeit, da er nach ganz neuen Methoden zur Quantifizierung verlangt: Die Raumzeit selbst muss quantifiziert werden.
Derzeit gibt es zwei unterschiedliche Ansätze, dies zu versuchen:
- Der erst betrachtet nur Gravitation — kümmert sich also nicht um noch andere Wechselwirkungen.
- Der zweite aber — heute wirklich nur durch Stringtheorie repräsentiert — geht davon aus, dass man von vornherein von einer vereinheitlichten Theorie aller Wechselwirkungen ausgehen müsse — an besten beginnend mit einem Zustand unseres Universums, in dem sich die Gravitation noch nicht von all den anderen Wechselwirkungen abgesondert hat.
Beitrag 0-354
Materiedichte im (heutigen) Universum = etwa 1 Atom pro 5 Kubikmeter
Wie leer kosmischer Raum heute ist

Quelle: Spatium, Apr 1998
Lies auch andere interessante Spatium-Artikel

Quelle: Spatium, Apr 1998
Lies auch andere interessante Spatium-Artikel
Beitrag 0-540
Wo auch heute noch selbst manche Physiker falsch argumentieren
In Sachbüchern für Physik
gelegentlich anzutreffende Denkfehler
gelegentlich anzutreffende Denkfehler
Falsch ist, dass ...
... es eine kleinste Portion von Energie gäbe (und jede andere ganzzahliges Vielfaches davon sei):
Im Buch A Big bang in a little Room (Zeya Morali, 2017) liest man auf Seite 32:... the smallest denomination that the energy of tiny particles can take is known as a quantum of energy: A photon can have 1 quantum of energy, or 2 quanta, or 72 quanta, or any other whole-number-multiple ... but not 3/4 of a quantuim, or 42+1/3 quanta of energy, say.
Das ist falsch, denn:Tatsächlich wahr ist, dass die Energie eines Photons stets gegeben ist als Produkt von Plancks Wirkungsquantum und der Frequenz des Photons. Letztere kann beliebig klein werden, wie z.B. die Tatsache beweist, dass kosmischer Raum — schon seit dem Urknall — expandiert und daher die Wellenlänge der Photonen (z.B. die der kosmischen Hintergrungstrahlung) sich ständig vergrößert.
Wie man sieht, verwechselt die Autorin des Buches Energie mit Wirkung: Ein ganz gravierender Fehler, der einer promovierten theoretischen Physikerin, die heute als Wissenschaftjournalist arbeitet, besser nicht unterlaufen sollte.
In ihrem Buch besonders aussagekräftig und wohl auch richtig dargestellt sind vor allem Inhalt und Geschichte der Inflationstheorie einschließlich der ewiger Inflation: Dieser Teil des Buches — Kapitel 3, 4 und 5 — ist auf jeden Fall lesenswert. Er berichtet, was die Urheber jener Theorien — Guth, Linde und Vilenkin — der Buchautorin in Interviews selbst mitgeteilt haben.
Mehr zum Buch insgesamt sagt Sabine Hossenfelders Rieview.
Mein Ratschlag: Wer an Kosmologie als Wissenschaft interessiert ist — statt an wilder, absolut unbegründeter Spekulation ergänzt um geradezu naiv anmutende Hinweise der Autorin auf Gott — lese die Kapitel 3 bis 5 des Buches, aber nichts weiter sonst.
|
Auf Seite 38 des Buches zeigt sich, dass Morali das wichtigste Experiment der Quantenphysik — das Doppelspaltexperiment — noch nicht richtig verstanden hat, und auch nicht Hugh Everett's Viele-Welten-Theorie. Sie schreibt:"According to Everett's speculation, when Suarez set up his double-slit experiment [...], the moment he made a quantum measurement of the path of the photon — to check if it took the left or the right slit — reality fractured, creating two almost identical clone universes. The only difference between the two would be that in one [...] Suarez detected that the photon traveled through the left slit, while at the same instant his parallel self in an alternative version of Zaragoza was recording the outcome that the photon had traveled through the right slit."
Tatsächlich richtig ist: Niemand kann beobachten, dass das Photon durch nur einen Spalt kommt: Es kommt IMMER durch beide.
Genauer: Beim Versuch, Pfadinformation zu erhalten, muss man hinter die Spalten Polarisationsfilter setzen, welche ankommendendes Licht spaltenspezifisch senkrecht zu einander polarisieren: Wie man feststellt, verschwindet dann die Interferenz (einfach deswegen, da senkrecht zu einander polarisiertes Licht nicht interferieren kann). Leider scheint das bisher auch einigen anderen Physikern noch gar nicht so richtig klar zu sein. Sie stellen dann das Verschwinden der Interferenz beim Versuch, Pfadinformation zu erhalten, als großes Geheimnis hin: als etwas Unerklärbares, das mit beitrage zur angeblichen "Unverständlichkeit" des Quantenverhaltens.
Schlimmer noch: Der Physiker David Deutsch argumentiert in seinem Buch The Fabric of Reality (1997) allen Ernstes, dass das Doppelspaltexperiment die Existenz der "vielen Welten" im Sinne von Hugh Everett III beweise. Er denkt wirklich — wie Morali ja auch —, sie alle würden in gleich konkreter Weise existieren. Tatsächlich aber existieren sie nur als logische Gebilde im Konfigurationsraum aller Möglichkeiten, über deren Eintreten oder Nicht-Eintreten die Zukunft entscheiden wird.
Falsch ist, dass ...:
... es unter unendlich viele Paralleluniversionen mindestens zwei mit genau gleichem Inhalt geben muss,
oder ein Affe, wenn er nur hinreichend lange tippen könnte, mit Sicherheit irgendwann Shakespears gesammelte Werke reproduziert haben würde.
Beides wird von zahlreichen Sachbuchautoren — gelegentlich auch von Professoren der Physik, u.A. von Alexander Vilenkin — so behauptet. Genauer:
Einige Kosmologen — und z.B. auch zahlreiche populärwissenschaftliche Darstellungen der Multiversentheorie — stellen es als selbstverständlich hin, dass alles, was möglich ist, in irgend einem (sog. Parallel-) Universum auch tatsächlich vorkomme. Die Wahrscheinlichkeitstheorie, so schreiben sie, würde es beweisen, wenn man davon ausgehe, dass es unendlich viele Universen gäbe.
Aber tut sie das wirklich? Ganz offensichtlich nicht, denn:
Wer sich eine Menge von N gleich wahrscheinlichen Teilchenkonfigurationen vorstellt, wird zu Recht behaupten können, die Wahrscheinlichkeit dafür, dass eine ganz bestimmte davon wirklich auftritt, sei 1/N (also positiv). Wenn nun aber N gegen unendlich strebt, strebt 1/N gegen Null. Betrachtet man also eine unendlich große Menge möglicher Zustände eines Universums, kann nicht mehr behauptet werden, die Wahrscheinlichkeit dafür, dass ein ganz bestimmter davon wirklich eintreten werde, sei positiv. Ebenso wenig kann behauptet werden sie sei Null. Sie ist also undefiniert, und somit kann man weder sicher sein, dass sich der fragliche Zustand ergibt, noch kann man sicher sein, dass er sich nicht ergibt.
Man erkennt: Nicht jede Argumentation, die im Falle nur endlich vieler Alternativen schlüssig wäre, kann auch noch angewandt werden, wo es sich um mehr als nur endlich viele Alternativen handelt.
Beitrag 2113-1
Nachweis einer Klarstellung zur SRT
In Wikipedia wird völlig richtig erklärt:
Bewegte Uhren scheinen langsamer zu gehen:
Jeder Beobachter, relativ zu dem die Uhr sich bewegt, hat diesen Eindruck.
Das Ausmaß allerdings, in dem unterschiedliche Beobachter eine bewegte Uhr langsamer gehen sehen, kann von Beobachter zu Beobachter verschieden groß sein. Kurz:
Wie schnell ein Beobachter eine Uhr gehen sieht,
hängt davon ab, wie schnell er sich ihr gegenüber bewegt.
Man kann das einsehen wie folgt:
Kleine Übungsaufgabe:
Nun, Okotombrok,
so richtig verstanden hast Du die SRT wohl nicht, denn auch Physiker betonen, dass die SRT nur von beobachterspezifischen S i c h t e n spricht, aber keineswegs von Raumstruktur:
Quelle: Seite 212 des Buches Gottes unsichtbare Würfel von Helmut Satz (Verlag C.H. Beck 2013)
Der Autor — Helmut Satz — war von 1971 bis 2001 Professor für Theoretische Physik an der Universität Bielefeld.
Fast noch deutlicher wird Grtgrt bestätigt durch Bojowald:
Quelle: Seite 24 des Buches Zurück vor den Urknall von Martin Bojowald (Fischer Taschenbuchverlag, 3. Auflage 2012)
Martin Bojowald lehrt Theoretische Physik an der Penn State University, USA.
Völlig richtig wird der wahre Sachverhalt auch beschrieben durch Carrier. Seine Formulierung enthält auch eine Begründung:
Insbesondere sagt Carrier (nach Erklärung eines scheinbaren Paradoxons):
Quelle: Seite 33-39 des Buches Raum-Zeit von Martin Carrier (de Gruyter 2009)
Carrier ist Professor für Philosophie an der Universität Bielefeld mit Schwerpunkt Wissenschaftsphilosophie
Er begann seine Ausbildung mit einem Studium der Physik.
Man lese auch
Bewegte Uhren scheinen langsamer zu gehen:
Das Ausmaß allerdings, in dem unterschiedliche Beobachter eine bewegte Uhr langsamer gehen sehen, kann von Beobachter zu Beobachter verschieden groß sein. Kurz:
hängt davon ab, wie schnell er sich ihr gegenüber bewegt.
Man kann das einsehen wie folgt:
-
Hat man zwei Objekte, die sich mit konstanter Geschwindigkeit von einander weg bewegen, so wird jedes von beiden den Eindruck haben, die Zeit beim jeweils anderen vergehe langsamer.
Da sich diese beiden Beobachtungen aber widersprechen, steht fest, dass es sich hierbei um einen nur beobachtungstechnisch bedingten Effekt handelt: um ein Scheinergebnis,
welches sich der Realität des Beobachters zuordnet, aber nicht Wirklichkeit sein muss.
Und tatsächlich gilt ja im Rahmen von Einsteins Theorie immer:
Jede Beobachtung ist ihrem Ergebnis nach abhängig vom Bezugssystem, aus dem heraus der Beobachter argumentiert.
Anders gesagt: Wir sprechen stets nur über beobachterspezifische Realität
Kleine Übungsaufgabe:
-
Nimm an, wir hätten einen Schienenweg, der einen Kreis darstellt. Irgendwo auf dieser eingleisigen, kreisförmigen Strecke stehen zwei baugleiche Lokomotiven,
deren Rückseiten sich berühren und die zum selben Zeitpunkt
in entgegengesetzte Richtung abfahren, stets identisch beschleunigt werden, aber anhalten in dem Moment, in dem sie sich wieder berühren (sie kommen ja nicht an einander vorbei).
Beide, so nehmen wir an, transportieren baugleiche Uhren, die beim Start der Lokomotiven 12:00 zeigten.
- die jeweils andere langsamer ging, solange der Abstand zwischen ihnen sich vergrößert hat
- bzw. schneller ging, sobald der Abstand zwischen ihnen sich wieder verkleinerte.
FRAGE: Werden die beiden Uhren unterschiedliche Zeit anzeigen, wenn die beiden Lokomotiven wieder aufeinander treffen? (Sie werden dann jeweils genau gleich weit gefahren sein.) Wie verträgt sich deine Antwort mit der Tatsache, dass während der Fahrt aus Sicht jeder der beiden Uhren
Okotombrok in 1997-99:
Grtgrt in 1997-94:
Das Szenario symmetrisch zu machen erlaubt uns zu erkennen, dass — in der SRT —
die beobachtete Zeitdilation nur in den S i c h t e n der beiden Beobachter auftritt, aber eben n i c h t in der Raumzeit selbst.
Dummes Zeug,
das einzige, was dein Szenario erkennen lässt ist, dass unter gleichen Bedingungen Bedingungen herrschen, die zu gleichen Bedingungen führen.
Nun, Okotombrok,
so richtig verstanden hast Du die SRT wohl nicht, denn auch Physiker betonen, dass die SRT nur von beobachterspezifischen S i c h t e n spricht, aber keineswegs von Raumstruktur:
Zitat von Helmut Satz (2013):
Wenn in einem Raumschiff, das sich mit einer hohen konstanten Geschwindigkeit v relativ zur Erde bewegt, die Lichtgeschwindigkeit c die gleiche ist, wie in einem irdischen Labor, dann muss aus unserer Sicht das Längenmaß des Raumschiffes kürzer sein als unseres oder deren Uhr muss langsamer sein als unsere oder beides.
In der Tat tritt beides auf. Ein festes Maß d0. ein Standardmeter, hat den gleichen Wert für uns hier wie für die Passagiere des Raumschiffs.
Aber von uns aus gemessen erscheint deren Standardmeter d0 auf eine Länge d geschrumpft
d = d0 • ( 1 – (v/c)2 )1/2
Und ein festes Zeitintervall t0 erscheint, von der Erde ais gesehen, länger geworden zu sein, den Wert
t = t0 • ( 1 – (v/c)2 )–1/2
zu haben.
Der Autor — Helmut Satz — war von 1971 bis 2001 Professor für Theoretische Physik an der Universität Bielefeld.
Fast noch deutlicher wird Grtgrt bestätigt durch Bojowald:
Zitat von Martin Bojowald (2008):
Wenn wir uns beim Betrachten einer Situation schneller bewegen als ein zweiter Beobachter, so erscheinen uns räumliche und zeitliche Abstände in den beobachteten Ereignissen anders als diesem.
Wie ein Wechsel des Sichtwinkels die räumlichen Ausdehnungen ineinander überführt, so wandelt ein Ändern der Geschwindigkeit beim Beobachten räumliche in zeitliche Abstände um und umgekehrt.
Aus diesem Grunde ist die Unterscheidung zwischen räumlicher und zeitlicher Ausdehnung vom Standpunkt (oder genauer von der "Standbahn", wenn wir uns wirklich bewegen) abhängig und hat keine physikalische Basis unabhängig von Beobachtern. Anstatt Raum und Zeit zu trennen, gibt es nur ein einziges gemeinsames Objekt: die Raumzeit.
Martin Bojowald lehrt Theoretische Physik an der Penn State University, USA.
Völlig richtig wird der wahre Sachverhalt auch beschrieben durch Carrier. Seine Formulierung enthält auch eine Begründung:
Zitat von Martin Carrier (2009):
Kennzeichnend für die SRT ist der Vorrang raumzeitlicher Größen vor ihren räumlichen und zeitlichen Bestandteilen. Dieser Primat der 4-dimensionalen Größen wurde zuerst 1908 von Minkowski hervorgehoben: Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.
Minkowski erkannte, dass sich die SRT als eine spezifische, neuartige Geometrie darstellen lässt, in der die raumzeitlichen Abstände eine zentrale Stellung insofern einnehmen, als sie die o b j e k t i v e n Beziehungen zwischen Ereignissen wiedergeben, während deren räumliche und zeitliche Bestimmungsstücke vom Bewegungszustand des Beobachters abhängen und in diesem Sinne s u b j e k t i v sind.
Genauer: Der [mit Hilfe der Minkowski-Metrik errechnete] Viererabstand ist die zentrale Größe der Raumzeit der SRT. Im Unterschied zur Raum-Zeit der klassischen Physik bleibt allein diese Größe bei einem Wechsel des Inertialsystems erhalten — nicht aber der 3-dimensionale räumliche Abstand oder der 1-dimensionale zeitliche.
Wegen dieser Invarianz ist der Viererabstand fundamentaler [ der Wirklichkeit näher ] als die vom Bezugssystem abhängigen räumlichen und zeitlichen Größen.
Dennoch ist es nicht die 4-Dimensionalität als solche, die die Relativitätstheorie auszeichnet: Auch Ereignisse in der Newtonschen Raum-Zeit werden ja erst durch 3 Ortskoordinaten und eine Zeitkoordinate vollständig lokalisiert. Kennzeichnend für die SRT ist vielmehr der Vorrang raumzeitlicher Größen vor ihren räumlichen und zeitlichen Bestandteilen. ...
Insofern beinhaltet der Übergang von der Newtonschen zur Einsteinschen Raumzeit die Ersetzung 3-dimensionaler bzw. 1-dimensionaler absoluter Größen durch jeweils nur e i n e 4-dimensionale absolute Größe.
Insbesondere sagt Carrier (nach Erklärung eines scheinbaren Paradoxons):
Zitat von Martin Carrier (2009):
Deutlich wird, dass die relativistische Längenkontraktion eine Folge des Verfahrens der Längenmessung ist.
Carrier ist Professor für Philosophie an der Universität Bielefeld mit Schwerpunkt Wissenschaftsphilosophie
Er begann seine Ausbildung mit einem Studium der Physik.
Man lese auch
- G. Greiter: Relativitätstheorie beschreibt beobachterspezifische Realität
- G. Greiter: Zeitdilatation im Sinne der Theorien Einsteins
Beitrag 2103-1
Überlichtgeschwindigkeit — eine Klarstellung und 2 Beispiele
Überlichtgeschwindigkeit – es gibt sie auch in SRT und ART
Ein weit verbreiteter Irrtum besteht darin, zu glauben, dass es keine Geschwindigkeiten höher als die des Lichts gibt.
Tatsächlich gibt es beliebig hohe Geschwindigkeiten auch im Rahmen der beiden Relativitätstheorien. Beide — die SRT und auch die ART — beweisen lediglich, dass kein Signal sich schneller als das Licht bewegen kann.
Signal in diesem Sinne ist alles,
das sich auf der Geodäte der Raumzeit bewegt, die den Beobachter mit dem beobachteten Objekt verbindet
( in der SRT also auf einer Geraden, die durch den Beobachter führt ).
Eine gut verständliche Begründung — und auch zwei Beispiele — finden sich auf den Seiten 106 bis 111 des Buches Spezielle Relativitätstheorie des Physikers Domenico Giulini (erschienen 2004 im Fischer Taschenbuch Verlag):
Hier nun die beiden Beispiele für tatsächlich b e o b a c h t b a r e Überlichtgeschwindigkeit, die Giulini im Detail diskutiert:
Vorsicht aber: B e o b a c h t e t e Geschwindigkeiten sind Scheingeschwindigkeiten, die für zueinander bewegte Beobchter u n t e r s c h i e d l i c h hohen Wert haben (als mit Sicherheit keine reale Geschwindigkeit darstellen).
Beispiel 1 (nachgerechnet auf Basis der SRT):
Beispiel 2 (auf Basis ART, da durch astronomische Beobachtung entdeckt):
PS 1: Diese Beispiele zeigen einmal mehr, dass — worauf ich hier im Forum schon mehrmals zu sprechen kam — durch Beobachter gemessene Geschwindigkeiten stets nur S i c h t auf eine Signalgeschwindigkeit sein können (niemals aber wirklich reale Geschwindigkeiten sind). Mit anderen Worten:
Es gilt zu unterscheiden zwischen
Erst wer das verstanden hat, kann verstanden haben, wie die SRT denn nun wirklich argumentiert und was ihre Aussagen tatsächlich bedeuten.
PS 2: Man sollte sich zudem klar machen, dass die Raumzeit — ausgestattet mit der Minkowski-Metrik — nur eine einzige r e a l e Geschwindigkeit kennt: die des Lichts.
Denn alles, was man sonst noch so an Geschwindigkeiten kennt, sind einfach nur beobachter-spezifische S i c h t e n , die sich ergeben
Ein weit verbreiteter Irrtum besteht darin, zu glauben, dass es keine Geschwindigkeiten höher als die des Lichts gibt.
Tatsächlich gibt es beliebig hohe Geschwindigkeiten auch im Rahmen der beiden Relativitätstheorien. Beide — die SRT und auch die ART — beweisen lediglich, dass kein Signal sich schneller als das Licht bewegen kann.
das sich auf der Geodäte der Raumzeit bewegt, die den Beobachter mit dem beobachteten Objekt verbindet
( in der SRT also auf einer Geraden, die durch den Beobachter führt ).
Eine gut verständliche Begründung — und auch zwei Beispiele — finden sich auf den Seiten 106 bis 111 des Buches Spezielle Relativitätstheorie des Physikers Domenico Giulini (erschienen 2004 im Fischer Taschenbuch Verlag):
Zitat von Giulini:
Wird die Frage » Gibt es Überlichtgeschwindigkeiten? « in dieser Allgemeinheit gestellt, so muss sie mit einem klaren JA beantwortet werden:
Nur bestimmten Ausbreitungsphänomenen setzt die SRT den Wert c als Grenze. Dies betrifft ... allgemein alle Prozesse, die zumindest im Prinzip einer Signalübertragung dienen können, wobei man hier allerdings eine sorgfältige Definition von » Signal « anfügen müsste. Auf jeden Fall würde eine Signalausbreitung mit Überlichtgeschwindigkeit innerhalb der SRT zu Widersprüchen in Kausalitätsverhältnissen führen.
Hier nun die beiden Beispiele für tatsächlich b e o b a c h t b a r e Überlichtgeschwindigkeit, die Giulini im Detail diskutiert:
Vorsicht aber: B e o b a c h t e t e Geschwindigkeiten sind Scheingeschwindigkeiten, die für zueinander bewegte Beobchter u n t e r s c h i e d l i c h hohen Wert haben (als mit Sicherheit keine reale Geschwindigkeit darstellen).
Beispiel 1 (nachgerechnet auf Basis der SRT):
- Giulini betrachtet einen Beobachter B, der im Ursprung eines Inertialsystems sitzt und ein Objekt X beobachtet, das sich auf einer Geraden mit gleichförmiger Geschwindigkeit bewegt. Diese Gerade führe nicht durch den Beobachter, wohl aber durch einen Punkt P. Bezeichnet nun a den spitzen Winkel zwischen dieser Geraden und der Strecke von B nach P, so kommt Giulini über einige wenige Rechenschritte hin zur Aussage, dass für die durch B beobachtete Geschwindigkeit v(B) des Objekts X
- gilt, wenn man
- setzt und hierbei unter v die Geschwindigkeit versteht, mit der sich X als Signal seiner Bahn entlang durch den 3-dimensionalen Raum bewegt.
- Für ein festes Verhältnis v/c und variablen Winkel a erreicht die Funktion s(a,v) ihr Maximum bei cos(a) = v/c . Dort ist dann also
- was für v gegen c nach unendlich strebt, so dass also tatsächlich v(B) auch weit größer als c werden kann.
Beispiel 2 (auf Basis ART, da durch astronomische Beobachtung entdeckt):
Zitat von Giulini:Heute kennt man in der Astronomie zahlreiche Beispiel für diesen Effekt [ beobachteter Überlichtgeschwindigkeit ].
Ein besonders eindrucksvolles liefert die Galaxie M87, die sich in einer Entfernung von 60 Mio Lichtjahren von uns im Virgohaufen befindet. Aus ihrem Zentrum werden Gasströme entlang sog. Jets auf einer Länge von 5000 Lichtjahren ins All geschleudert, deren gemessene visuelle Geschwindigkeit v(B) die 6-fache Lichtgeschwindigkeit erreichen!.
Getrieben werden diese Jets wahrscheinlich durch ein im Zentrum der Galaxie vorhandenes supermassives Schwarzes Loch. Man schätzt die eigentliche Geschwindigkeit v der Gasströmung [ die also, die sie als Signal hat ] auf höchstens 98% der Lichtgeschwindigkeit.
PS 1: Diese Beispiele zeigen einmal mehr, dass — worauf ich hier im Forum schon mehrmals zu sprechen kam — durch Beobachter gemessene Geschwindigkeiten stets nur S i c h t auf eine Signalgeschwindigkeit sein können (niemals aber wirklich reale Geschwindigkeiten sind). Mit anderen Worten:
Es gilt zu unterscheiden zwischen
- scheinbarer ( d.h. beobachteter ) Geschwindigkeit einerseits und
- Signalgeschwindigkeit andererseits (nur sie kann niemals höher als Lichtgeschwindigkeit sein; ihre Richtung ist stets tangential zu einer Geodäte).
Erst wer das verstanden hat, kann verstanden haben, wie die SRT denn nun wirklich argumentiert und was ihre Aussagen tatsächlich bedeuten.
PS 2: Man sollte sich zudem klar machen, dass die Raumzeit — ausgestattet mit der Minkowski-Metrik — nur eine einzige r e a l e Geschwindigkeit kennt: die des Lichts.
Denn alles, was man sonst noch so an Geschwindigkeiten kennt, sind einfach nur beobachter-spezifische S i c h t e n , die sich ergeben
- entweder als Projektion von Signalgeschwindigkeit in der Raumzeit auf den 3-dimensionalen Raum
- und/oder als Schrumpfen oder Wachsen von Abständen (pro Zeiteinheit) zweier vom Beobachter ins Auge gefasster Objekte aus der spezifischen Perspektive des Beobachters und seiner Uhr heraus.
Beitrag 1057-123
Klarstellung zu unvorstellbar großer Geschwindigkeit
Sei gegrüßt, E...,
aber glaube mir: Selbst die Verfechter der Inflationstheorie behaupten nirgendwo, dass sich das Universum — wann auch immer und über wie kurze Zeit auch immer — mit unendlich großer Geschwindigkeit ausgedeht hätte.
Der Grund hierfür: Es gibt einfach keine unendlich große Geschwindigkeiten.
Genauer: Es gibt sie nur in der Umgangssprache (als wenig genaues Synonym zum Begriff unvorstellbar großer Geschwindigkeit). Aber selbst eine unvorstellbar große Geschwindigkeit ist eine endlich große Geschwindigkeit.
Wo in der Physik eine Größe gegen Unendlich (oder gar nicht) zu konvergieren scheint, bedeutet das einfach nur, dass unser Modell an dieser Stelle versagt und durch ein genaueres ersetzt werden müsste. Es zu finden, ist das große Problem.
Interessant ist übrigens, dass die Stringtheorie Modelle kennt, die in dem Sinne zueinander dual sind, dass sie
Wie Heisenbergs Unschärferelation uns zeigt, macht es keinen Sinn, beliebig kleine physikalische Objekte zu erwarten (die Planck-Skala scheint eine untere Grenze für ihre Größe darzustellen). Manchmal frage ich mich, ob es nicht dual dazu auch eine obere Grenze für die Größe physikalischer Objekte geben könnte.
Gruß, grtgrt
E... aus 1057-115:Hallo Grtgrt, sei gegrüßt.Grtgrt aus 1057-113:(...)
Wenn dem so wäre, müsste sich unser Universum wenigstens kurze Zeit mit unendlich großer Geschwindigkeit ausgedehnt haben — was nicht denkbar ist.
(...)
Ungeachtet dessen was Dir denkbar erscheint, versuch es mal hier (als groben Überblick)
http://de.wikipedia.org/wiki/Alan_H._Guth und hier http://de.wikipedia.org/wiki/Inflation_%28Kosmologie%29
Weitere Links stehen mannigfaltig zur Verfügung.
Sei gegrüßt, E...,
aber glaube mir: Selbst die Verfechter der Inflationstheorie behaupten nirgendwo, dass sich das Universum — wann auch immer und über wie kurze Zeit auch immer — mit unendlich großer Geschwindigkeit ausgedeht hätte.
Der Grund hierfür: Es gibt einfach keine unendlich große Geschwindigkeiten.
Genauer: Es gibt sie nur in der Umgangssprache (als wenig genaues Synonym zum Begriff unvorstellbar großer Geschwindigkeit). Aber selbst eine unvorstellbar große Geschwindigkeit ist eine endlich große Geschwindigkeit.
Wo in der Physik eine Größe gegen Unendlich (oder gar nicht) zu konvergieren scheint, bedeutet das einfach nur, dass unser Modell an dieser Stelle versagt und durch ein genaueres ersetzt werden müsste. Es zu finden, ist das große Problem.
Interessant ist übrigens, dass die Stringtheorie Modelle kennt, die in dem Sinne zueinander dual sind, dass sie
- einerseits identische physikalische Gesetzmäßigkeit darstellen,
- andererseits aber so zueinander "isomorph" sind, dass, was im einen Modell seiner Größe nach gegen Null geht im anderen seiner Größe nach gegen Unendlich geht.
Wie Heisenbergs Unschärferelation uns zeigt, macht es keinen Sinn, beliebig kleine physikalische Objekte zu erwarten (die Planck-Skala scheint eine untere Grenze für ihre Größe darzustellen). Manchmal frage ich mich, ob es nicht dual dazu auch eine obere Grenze für die Größe physikalischer Objekte geben könnte.
Gruß, grtgrt
Beitrag 1057-156
Weitere Klarstellungen
Ich schrieb:
Bei einer Explosion bleiben die Trümmerstücke gleich groß.
Bei der Expansion des Alls wachsen alle Teilbereiche gleich schnell an.
Das ist der Unterschied zwischen beiden Vorgängen; so wie ich auch in Beitrag 1057-148 an den anderen Beschreibungspaaren den Unterschied zwischen Expansion und Explosion gegenüberstelle.
Natürlich ist die kosmische Expansionsgeschwindigkeit überall gleich, aber im Endeffekt wirkt es sich so aus, daß man von jedem Punkt des Universums ein anderes Bild erhält. Der Dopplereffekt des Schalls führt auch dazu, daß wir bewegte Sirenen eines Fahrzeugs anders hören, obwohl der ausgesandte Ton stets gleich bleibt. Ein stehender-, ein sich entfernender- und ein auf die Sirene zukommender Autofahrer hat von ein und demselben Ausgangston einen anderen Höreindruck.
Bei einer Explosion im kräftefreien Raum bleibt die Geschwindigkeit der Trümmerstücke gleich.
Jedes Explosions-Teilchen behält seine individuelle Geschwindigkeit bei, wenn keine Kräfte auf es wirken. Jeder Teilbereich des expandierenden Universums beschleunigt aber im laufe der Zeit, im Bezug zum Standort eines Beobachters. Das hatte ich ja eben gerade beschrieben.
Und ich erinnere mich an Deinen Satz: "...Der Kosmos hat nur eine Geschwindigkeit, mit der er sich ausdehnt und keine Teilbereiche...". Nun hat er also doch Teilbereiche?
Schwamm drüber.
Ich las in irgendeiner Ausgabe eines Wissenschaftsmagazins, daß man darüber nachdenkt ob das Universum sich vielleicht doch nicht insgesamt gleichmäßig ausdehnt. Warum sollte es auch? Daß es aus einer Singularität entstand, daran glaubt schon seit Mitte der 1980-er Jahre selbst Stephen Hawking nicht mehr (steht in "Eine kurze Geschichte der Zeit").
Wie ich schon früher beschrieben habe, stelle ich mir vor, daß das Universum schon vor dem Ereignis "Urknall" existierte, und eine sehr hohe Dichte und eine bestimmte Größe hatte. Sagen wir mal einen Radius von mindestens 16 Mrd Lj., so daß wir nicht in der "Mitte" sein müssen-, aber auch nicht die "Begrenzung" erkennen können. Das Universum war damals "anders" als heute. Irgendwann geschah eine Veränderung dieses Zustandes und es begann zu expandieren. Die gleichförmige Hintergrundstrahlung ergibt sich dabei nicht aus der Kleinheit am Anfang, sondern aus der überall gleich hohen Dichte. Wenn ich vor mir 2 Flaschen mit Mineralwasser stehen habe, die kurz hintereinander in derselben Anlage abgefüllt wurden, haben sie denselben Innendruck und einen gleichen Inhalt. Wenn ich nun den Verschluß öffne, werden in beiden Flaschen die gleichen Abläufe passieren, ohne daß sie miteinander verbunden sind. Natürlich wird es geringe Abweichungen geben, aber gleiche Ausgangssituationen ergeben auch gleiche Abläufe in den ersten Momenten. Die Chaosforschung zeigt, daß sich nach längerer Zeit natürlich Unterschiede ergeben. Aber wenn das Universum auf seine maximale Dichte zusammengepresst war (nicht auf eine "Singularität"), sollte es auch überall fast gleich expandieren. Fast! Es kann aber eben auch sein, daß die Expansionsgeschwindigkeit in verschiedenen Bereichen der RaumZeit unterschiedlich ist.
Schönen Sonntag noch
Bernhard
Ich eher den ersten, aber modifiziert. Der Urknall ist der Zeitpunkt des Expansionsbeginns. Über die Ursache können wir nur spekulieren. Die Expansion hält weiter an und beschleunigt sich, wie letztes Jahr die Nobelpreisträger nachwiesen.Henry aus 1057-151:...Es gibt tatsächlich zwei Vorstellungen darüber, was man mit "Urknall" meint. Die erste meint die urplötzlich auftauchende Expansion, die auch heute noch zu beobachten ist (dann wäre der Urknall noch gar nicht beendet), und die zweite meint den plötzlichen Ausbruch, der zur Expansion führte. Ich bevorzuge den zweiten Ansatz.
Hmm, dann habe ich das hier falsch interpretiert:Zitat:Ich habe überhaupt nicht behauptet, dass Expansion und Explosion dasselbe wären,
Du bestehst darin hartnäckig auf dem Begriff Explosion.Henry aus 1057-145:Laut Theorie war es ein spontanes, äußerst heftiges Ereignis. Ich denke, man kann so etwas mit Fug und Recht als Explosion bezeichnen;...
...wenn sich etwas innerhalb einer Sekunde um 300000 km ausdehnt, was also in etwa der Entfernung Erde- Mond entspricht – ja, wenn DAS keine Explosion ist, dann muss dieser Begriff wohl neu definiert werden.
Jetzt sind wir uns einig.Zitat:Wie wäre es denn mit explosionsartiger Expansion?
Warst du dabei? :smiley32: Wir sehen, daß bei einer gleichmäßigen Ausdehnungsgeschwindigkeit, die Summierung vieler Teilgeschwindigkeiten dazu führt, daß sich in derselben Zeit weit entfernte Bereiche schnelller voneinander entfernen, als nahe beieinander liegende Bereiche.Zitat:Was mir mit dem Beginn des Kosmos vorliegen haben, ist eine plötzliche, durch starke Kräfte verursachte Ausdehnung.
Ebend!Zitat:Was hat die gleich bleibende Größe der Trümmerstücke mit der Expansion des Kosmos zu tun? Die Expansion des Kosmos ist eine Expansion der Raumzeit, die hat überhaupt keine "Trümmerstücke".
Ich schrieb:
Bei einer Explosion bleiben die Trümmerstücke gleich groß.
Bei der Expansion des Alls wachsen alle Teilbereiche gleich schnell an.
Das ist der Unterschied zwischen beiden Vorgängen; so wie ich auch in Beitrag 1057-148 an den anderen Beschreibungspaaren den Unterschied zwischen Expansion und Explosion gegenüberstelle.
Das sehe ich anders. Die Ausdehnungsgeschwindigkeit steigt mit jedem Megaparsec Entfernung um 71km/s.Zitat:Der Kosmos hat nur eine Geschwindigkeit, mit der er sich ausdehnt und keine Teilbereiche,
Natürlich ist die kosmische Expansionsgeschwindigkeit überall gleich, aber im Endeffekt wirkt es sich so aus, daß man von jedem Punkt des Universums ein anderes Bild erhält. Der Dopplereffekt des Schalls führt auch dazu, daß wir bewegte Sirenen eines Fahrzeugs anders hören, obwohl der ausgesandte Ton stets gleich bleibt. Ein stehender-, ein sich entfernender- und ein auf die Sirene zukommender Autofahrer hat von ein und demselben Ausgangston einen anderen Höreindruck.
Ich behauptete ja auch nicht, daß sie für jedes Teilchen dieselbe ist. Ich schrieb:Zitat:Die Ausbreitungsgeschwindigkeit der Trümmerteilchen hängt in einem kräftefreien Raum einzig von der Energie ab, mit sie jeweils beschleunigt wurden. Und die ist überhaupt nicht für jedes Teilchen dieselbe,
Bei einer Explosion im kräftefreien Raum bleibt die Geschwindigkeit der Trümmerstücke gleich.
Jedes Explosions-Teilchen behält seine individuelle Geschwindigkeit bei, wenn keine Kräfte auf es wirken. Jeder Teilbereich des expandierenden Universums beschleunigt aber im laufe der Zeit, im Bezug zum Standort eines Beobachters. Das hatte ich ja eben gerade beschrieben.
Muss er das?Zitat:...und es muss auch jeder Teilbereich dieselbe Geschwindigkeit haben, weil der Kosmos als Gesamtheit in einem winzigen Bereich entstand,
Und ich erinnere mich an Deinen Satz: "...Der Kosmos hat nur eine Geschwindigkeit, mit der er sich ausdehnt und keine Teilbereiche...". Nun hat er also doch Teilbereiche?
Schwamm drüber.
Ich las in irgendeiner Ausgabe eines Wissenschaftsmagazins, daß man darüber nachdenkt ob das Universum sich vielleicht doch nicht insgesamt gleichmäßig ausdehnt. Warum sollte es auch? Daß es aus einer Singularität entstand, daran glaubt schon seit Mitte der 1980-er Jahre selbst Stephen Hawking nicht mehr (steht in "Eine kurze Geschichte der Zeit").
Wie ich schon früher beschrieben habe, stelle ich mir vor, daß das Universum schon vor dem Ereignis "Urknall" existierte, und eine sehr hohe Dichte und eine bestimmte Größe hatte. Sagen wir mal einen Radius von mindestens 16 Mrd Lj., so daß wir nicht in der "Mitte" sein müssen-, aber auch nicht die "Begrenzung" erkennen können. Das Universum war damals "anders" als heute. Irgendwann geschah eine Veränderung dieses Zustandes und es begann zu expandieren. Die gleichförmige Hintergrundstrahlung ergibt sich dabei nicht aus der Kleinheit am Anfang, sondern aus der überall gleich hohen Dichte. Wenn ich vor mir 2 Flaschen mit Mineralwasser stehen habe, die kurz hintereinander in derselben Anlage abgefüllt wurden, haben sie denselben Innendruck und einen gleichen Inhalt. Wenn ich nun den Verschluß öffne, werden in beiden Flaschen die gleichen Abläufe passieren, ohne daß sie miteinander verbunden sind. Natürlich wird es geringe Abweichungen geben, aber gleiche Ausgangssituationen ergeben auch gleiche Abläufe in den ersten Momenten. Die Chaosforschung zeigt, daß sich nach längerer Zeit natürlich Unterschiede ergeben. Aber wenn das Universum auf seine maximale Dichte zusammengepresst war (nicht auf eine "Singularität"), sollte es auch überall fast gleich expandieren. Fast! Es kann aber eben auch sein, daß die Expansionsgeschwindigkeit in verschiedenen Bereichen der RaumZeit unterschiedlich ist.
Schönen Sonntag noch
Bernhard
Beitrag 1896-34
Zwei Klarstellungen
Hallo ihr beiden (Irena & Henry),
eigentlich wollte ich das Thema nicht weiter diskutieren, da ich all meine Argumente ja schon genannt habe (und somit nichts mehr weiter zu sagen habe).
Mindestens zwei Klarstellungen sind aber wohl doch noch notwendig:
Ich habe nirgendwo behauptet, Gesetze seien Teil der Natur (wie du, Irena, mir hier in den Mund zu legen versuchst).
Meine Aussage war, das ich mathematische Gesetze für Naturgesetze halte.
Da gebe ich dir völlig recht.
Problem nur: Du unterstellst mir, dass ich durch den Gebrauch des Wortes modellieren hätte suggerieren wollen, dass wir so die Natur gestalten (statt nur den Versuch zu unternehmen, sei hinsichtlich gewisser Aspekte nachzubilden). Glaubst du im Ernst, dass das von mir so gemeint war?
Im übrigen kann ich nicht erkennen, dass sich irgendwer hier in diesem Forum präziser ausdrückt als ich. Die Unzweideutigkeit all unserer Formulierungen ist ja schon allein dadurch begrenzt, dass wir Umgangssprache nutzen (statt formaler Sprache).
Das ist wie in der Mathematik auch: Fast alle Beweise dort sind weitgehend in Umgangssprache niedergeschrieben, zerlegen also nur große Gedankensprünge in kleinere, deren Nachvollziehbarkeit man dann einfach als gegeben voraussetzt (obgleich sie bei einem Leser gegeben, beim anderen aber nicht gegeben sein kann). Alle Beweis in ausschließlich formaler Notation zu formulieren würde sie eindeutiger, aber keineswegs verständlicher machen. Ganz zu schweigen davon, dass unser Leben dann einfach zu kurz wäre, mehr als nur recht seichte Aussagen wirklich zu beweisen ...
Auf jeden Fall muss ich euch beiden ins Stammbuch schreiben:
Richtig zu zitieren setzt voraus, dass man die zitierte Formulierung so interpretiert, wie der Kontext, in dem sie sich fand, suggeriert. Hättet ihr das getan, wäret ihr nie auf die Idee gekommen, mir zu unterstellen, dass ich gesagt hätte
Im Berlin steht eine Plastik, die Willy Brandt darstellt. Hat der Künstler damit die Person Willy Brandt modelliert oder nicht? Und wie vollständig?
Gruß, grtgrt
eigentlich wollte ich das Thema nicht weiter diskutieren, da ich all meine Argumente ja schon genannt habe (und somit nichts mehr weiter zu sagen habe).
Mindestens zwei Klarstellungen sind aber wohl doch noch notwendig:
Zitat von Irena:
Nehmen wie logisch deine Aussage auseinander:
"... Gesetze sind Teil der Natur". Lassen wir jetzt außen vor die Tatsache, dass es um die mathematische Gesetze geht. Wie kann Gesetze ein Teil der Natur sein? Die Natur ist ein System von physikalischen Objekten. Die Gesetze sind ein Merkmal der Natur. So etwa wie du würdest sagen "die Farbe ist ein Teil dieses Gegenstands".
Ich habe nirgendwo behauptet, Gesetze seien Teil der Natur (wie du, Irena, mir hier in den Mund zu legen versuchst).
Meine Aussage war, das ich mathematische Gesetze für Naturgesetze halte.
Zitat von Henry:
Und denkst du wirklich, dass "die theoretische Physik die Natur modelliert"? Könnte es nicht eher sein, dass die theoretische Physik Modelle darüber erstellt, wie sich bestimmte Sachverhalte in der Natur zueinander verhalten? Die Physiker finden die Natur vor, sie modellieren sie nicht.
Da gebe ich dir völlig recht.
Problem nur: Du unterstellst mir, dass ich durch den Gebrauch des Wortes modellieren hätte suggerieren wollen, dass wir so die Natur gestalten (statt nur den Versuch zu unternehmen, sei hinsichtlich gewisser Aspekte nachzubilden). Glaubst du im Ernst, dass das von mir so gemeint war?
Im übrigen kann ich nicht erkennen, dass sich irgendwer hier in diesem Forum präziser ausdrückt als ich. Die Unzweideutigkeit all unserer Formulierungen ist ja schon allein dadurch begrenzt, dass wir Umgangssprache nutzen (statt formaler Sprache).
Das ist wie in der Mathematik auch: Fast alle Beweise dort sind weitgehend in Umgangssprache niedergeschrieben, zerlegen also nur große Gedankensprünge in kleinere, deren Nachvollziehbarkeit man dann einfach als gegeben voraussetzt (obgleich sie bei einem Leser gegeben, beim anderen aber nicht gegeben sein kann). Alle Beweis in ausschließlich formaler Notation zu formulieren würde sie eindeutiger, aber keineswegs verständlicher machen. Ganz zu schweigen davon, dass unser Leben dann einfach zu kurz wäre, mehr als nur recht seichte Aussagen wirklich zu beweisen ...
Auf jeden Fall muss ich euch beiden ins Stammbuch schreiben:
Richtig zu zitieren setzt voraus, dass man die zitierte Formulierung so interpretiert, wie der Kontext, in dem sie sich fand, suggeriert. Hättet ihr das getan, wäret ihr nie auf die Idee gekommen, mir zu unterstellen, dass ich gesagt hätte
- alle Gesetze seien Naturgesetze oder
- Modellierung in meinem Sinne geschehe im Glauben oder in der Absicht, dadurch die Natur zu gestalten.
Im Berlin steht eine Plastik, die Willy Brandt darstellt. Hat der Künstler damit die Person Willy Brandt modelliert oder nicht? Und wie vollständig?
Gruß, grtgrt
Beitrag 1922-9
Eine Klarstellung (auch, aber nicht nur, was den Begriff » transzendent « betrifft)
An Henry und Gregor:
Eurer beider Reaktion zeigt mir, dass mein Beitrag 1922-1 folgender Klarstellung bedarf:
Wenn ich das Wort » transzendent « benutze, dann meine ich damit einfach nur etwas, das direkt wahrzunehmen uns der entsprechende Sinn fehlt, das sich aber hin und wieder — ganz selten — indirekt bemerkbar macht insofern, als uns etwas korreliert erscheint, wo wir beim besten Willen keinen Grund für eine solche Korrelation erkennen können: etwas, das uns dann als absolut zufällige, aber dennoch extrem erstaunliche Ähnlichkeit auffällt.
Lothar Schäfer spricht in solchen Fällen gerne von einem » geistigen Hintergrund « physikalischer Objekte oder von der » sich selbst bewussten « Natur — beides Begriffe, die ich für nicht jedem zumutbar halte — sie suggerieren geradezu Esoterisches.
Dennoch: Wer sein Buch gelesen hat, und wem dabei bewusst wurde, wie scharf und wirklich wissenschaftlich im besten Sinne des Wortes er analysiert, und wie sorgfältig er zusammengetragen hat, was tatsächlich extrem erstaunliche Ähnlichkeiten sind, kann kaum anders, als zuzugeben, dass da vielleicht doch eine Verbindung sein könnte, die sich unserer Wahrnehmung bisher entzogen hat.
Was nun speziell Anton Zeilinger angeht, so hat der die Gabe, in seiner Rolle als Wissenschaftler wirklich nichts zu behaupten, was er nicht belegen kann. ABER: In seiner Rolle als jemand, der seine Ergebniss auch geschickt zu vermarkten versteht, pfeift er keinen Journalisten zurück, wenn der in seiner Berichterstattung ein wenig übertreibt in dem Sinne, dass er mit Begriffen operiert, die etwas suggerieren, was eine breite Öffentlichkeit als sehr spektakulär empfinden muss, was aber — kritisch hinterfragt — der Sache dann doch nicht wirklich gerecht wird.
Beste Grüße,
Gebhard Greiter (grtgrt)
An Henry und Gregor:
Eurer beider Reaktion zeigt mir, dass mein Beitrag 1922-1 folgender Klarstellung bedarf:
Wenn ich das Wort » transzendent « benutze, dann meine ich damit einfach nur etwas, das direkt wahrzunehmen uns der entsprechende Sinn fehlt, das sich aber hin und wieder — ganz selten — indirekt bemerkbar macht insofern, als uns etwas korreliert erscheint, wo wir beim besten Willen keinen Grund für eine solche Korrelation erkennen können: etwas, das uns dann als absolut zufällige, aber dennoch extrem erstaunliche Ähnlichkeit auffällt.
Lothar Schäfer spricht in solchen Fällen gerne von einem » geistigen Hintergrund « physikalischer Objekte oder von der » sich selbst bewussten « Natur — beides Begriffe, die ich für nicht jedem zumutbar halte — sie suggerieren geradezu Esoterisches.
Dennoch: Wer sein Buch gelesen hat, und wem dabei bewusst wurde, wie scharf und wirklich wissenschaftlich im besten Sinne des Wortes er analysiert, und wie sorgfältig er zusammengetragen hat, was tatsächlich extrem erstaunliche Ähnlichkeiten sind, kann kaum anders, als zuzugeben, dass da vielleicht doch eine Verbindung sein könnte, die sich unserer Wahrnehmung bisher entzogen hat.
Was nun speziell Anton Zeilinger angeht, so hat der die Gabe, in seiner Rolle als Wissenschaftler wirklich nichts zu behaupten, was er nicht belegen kann. ABER: In seiner Rolle als jemand, der seine Ergebniss auch geschickt zu vermarkten versteht, pfeift er keinen Journalisten zurück, wenn der in seiner Berichterstattung ein wenig übertreibt in dem Sinne, dass er mit Begriffen operiert, die etwas suggerieren, was eine breite Öffentlichkeit als sehr spektakulär empfinden muss, was aber — kritisch hinterfragt — der Sache dann doch nicht wirklich gerecht wird.
- Beispiel 1: Im von Gregor gefundenen Artikel empfinde ich den Abschnitt 6 (aber auch NUR den) als eine derartige Übertreibung. [Allerdings würde ich die dort in Abschnitt 2 gegebene Definition des Begriffes » transzendent « lieber durch meine ersetzt sehen.�
- Beispiel 2: In der Berichterstattung über Anton Zeilingers Ergebnisse wird hin und wieder angedeutet, zukünftige Ereignisse wären — so sähe es aus — in der Lage, das Ergebnis ihnen vorangegangener Ereignisse mit zu beinflussen. Das klingt spektakulär, ist aber falsch, denn jene zukünftigen Ereignisse liefern nur den Schlüssel, in Daten, die man in der Vergangenheit gesammelt hat, Information zu entdecken, die ohne jenen Schlüssel einfach nicht entdeckbar ist. [Wer in Zeilingers Buch "Einsteins Spuk" das Kapitel "Teleportation von Nichts" gelesen hat — und insbesondere die letzte Seite daraus (Seite 311) — wird wissen, wovon ich spreche.�
Beste Grüße,
Gebhard Greiter (grtgrt)
Beitrag 1923-39
Gödels Satz - eine Klarstellung
Hi Henry,
natürlich ist es für Leute, die keine Vorlesungen über mathematische Logik gehört haben, schwierig, zu verstehen, was Gödels Satz genau sagt.
Wenn du mir nicht glaubst, dann glaube vielleicht Lothar Schäfer (habe eben jetzt im Index zu seinem Buch nachgesehen und bin so zu Seite 71 geführt worden, wo steht):
Der springende Punkt ist:
Jeder KALKÜL im Sinne von Gödels Satz ist nur EIN logisches System.
Die Mathematik als Ganzes (als Vereinigung ALL ihrer logischen Systeme) kann man vergleichen mit einer Ebene, die komplett überdeckt ist mit Kreisringen, die sämtlich denselben Mittelpunkt M haben. Jeder dieser Kreisringe R( K) entspricht EINEM der mathematischen Kalküle K, und es gilt:
Nochmals also: Verwechsle bitte nie die Mathematik mit nur einem einzigen formalen Kalkül.
Was ich als den Mittelpunkt M aller R(K) bezeichne ist im übrigen nichts anderes als das Axiom vom Widerspruch (Aristoteles hat es wohl als Erster in seiner überaus grundlegenden Bedeutung klar erkannt). Es ist Basis all unseres logischen Denkens.
Beste Grüße,
grtgrt
Hi Henry,
natürlich ist es für Leute, die keine Vorlesungen über mathematische Logik gehört haben, schwierig, zu verstehen, was Gödels Satz genau sagt.
Wenn du mir nicht glaubst, dann glaube vielleicht Lothar Schäfer (habe eben jetzt im Index zu seinem Buch nachgesehen und bin so zu Seite 71 geführt worden, wo steht):
Zitat von Schäfer:
In der Mathematik ist Gödels Theorem der Beweis, dass komplexe logische Systeme, wie Arithmetik, zu ihrer Begründung Postulate benötigen, die sie nicht mit ihren eigenen Lehrsätzen beweisen können, sondern nur mit Begriffen eines umfassenderen Systems, das sozusagen auf einer höheren Stufe operiert.
Kein mathematisches System ist in sich abgeschlossen, weil Axiome, die für den Beweis seiner Lehrsätze benötigt werden, sich nicht selbst beweisen können.
Der springende Punkt ist:
Die Mathematik als Ganzes (als Vereinigung ALL ihrer logischen Systeme) kann man vergleichen mit einer Ebene, die komplett überdeckt ist mit Kreisringen, die sämtlich denselben Mittelpunkt M haben. Jeder dieser Kreisringe R( K) entspricht EINEM der mathematischen Kalküle K, und es gilt:
- Aussagem in Inneren des Kreisringes R(K) sind die Axiome, auf denen K aufbaut (die K also nicht beweisen kann bzw. als wahr voraussetzt).
- Aussagen auf dem Kreisring R(K) sind all die Aussagen, die K beweisen kann.
- Alle weiteren Aussagen liegen ausserhalb von R(K). Sie zu beweisen benötigt man einen mächtigeren, dem K übergeordneten Kalkül. Auch der aber ist ein mathematischer Kalkül.
Nochmals also: Verwechsle bitte nie die Mathematik mit nur einem einzigen formalen Kalkül.
Was ich als den Mittelpunkt M aller R(K) bezeichne ist im übrigen nichts anderes als das Axiom vom Widerspruch (Aristoteles hat es wohl als Erster in seiner überaus grundlegenden Bedeutung klar erkannt). Es ist Basis all unseres logischen Denkens.
Beste Grüße,
grtgrt
Beitrag 1963-32
Wichtige Klarstellung
Hi,
hier der Antwort zum mit E... diskutierten Thema Wellenkollaps/Dekohärenz von einem Fachmann Joachim Schulz (siehe auch http://www.scilogs.de/wblogs/blog/quantenwelt/conte...) aus Quantenforum ( http://www.quantenforum.de/viewtopic.php?f=6&t=... ):
Gruß Irena
Hinweis von grtgrt:
hier der Antwort zum mit E... diskutierten Thema Wellenkollaps/Dekohärenz von einem Fachmann Joachim Schulz (siehe auch http://www.scilogs.de/wblogs/blog/quantenwelt/conte...) aus Quantenforum ( http://www.quantenforum.de/viewtopic.php?f=6&t=... ):
Zitat:Ja, genau. Der neue Zustand nach dem Kollaps ist wieder ein Quantenzustand, der durch eine neue, reduzierte Wellenfunktion beschrieben wird. Es ist nicht so, dass da aus einer Welle ein klassisches Teilchen entsteht, das von da an keine Welleneigenschaften mehr hat. Die Welt bleibt quantenmechanisch.
Gruß Irena
Hinweis von grtgrt:
Wichtig noch:
Die Wellenfunktion — bzw. der Zustand nach dem Kollaps — ist nicht wirklich reduziert, sondern e r s c h e i n t uns nur so, da man den Zustand ja stets als Linearkombination zweier zueinander orthogonaler Zustände darstellt (gegeben durch die Messfrage). Nach dem "Kollaps" aber ist einer dieser beiden Zustände aber der, in den die "Messung" das Quant gebracht hat.
Der hin und wieder angetroffene Begriff » reiner Zustand « ist stets nur relativ zur Messfrage wohldefiniert, denn Antwort auf eine quantenphysikalische Messfrage kann ganz grundsätzlich stets nur ein JA oder ein NEIN sein.
So kann man z.B. ein Photon nicht nach seiner Polarisierung fragen. Man kann stets nur eine der — unendlich vielen — möglichen Polarisierungsrichtungen R vorgeben und dann fragen: » Liebes Photon, bist du in Richtung R polarisiert? «
Die Antwort wird ein JA oder ein NEIN sein — und das auch dann, wenn das Photon vor seinem Zusammentreffen mit der Messapparatur in einer Richtung polarisiert gewesen sein sollte, die weder R noch senkrecht zu R war:
Ergebnis einer Messung ist eben stets nur Wissen über den Zustand des Photons n a c h der Messung.
Beitrag 2035-29
Zwei Klarstellungen
Hallo Henry,
ich habe mir erlaubt, zwei deiner Feststellungen in das Glossar der Arbeitsplattform SRT in der nachstehenden Form einzubringen:
M.f.G. Eugen Bauhof
Wichtig zu wissen ist auch:
Die Aussage "Wenn wir laufen, während ein anderer Mensch still steht, dann vergeht auch für uns die Zeit langsamer, aber halt extrem wenig" ist falsch.
Henry aus 2035-27:Einige Grundlagen sollten mal wieder ins Gedächtnis gerufen werden!
Hallo Henry,
ich habe mir erlaubt, zwei deiner Feststellungen in das Glossar der Arbeitsplattform SRT in der nachstehenden Form einzubringen:
Zitat:Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
M.f.G. Eugen Bauhof
Wichtig zu wissen ist auch:
Die Aussage "Wenn wir laufen, während ein anderer Mensch still steht, dann vergeht auch für uns die Zeit langsamer, aber halt extrem wenig" ist falsch.
-
Es ist lediglich so, dass es der Laufende den Eindruck hat, die Uhr einer stehenden Person würde langsamer gehen als seine eigene (wenn er von ihr weg läuft).
Umgekehrt hat die stehende Person den Eindruck, die Uhr eines Läufers würde langsamer gehen als die eigene, solange er sich entfernt (bzw. schneller gehen, wenn der Laufende näher kommt).
In Wirklichkeit aber altern beide gleich schnell (solange sie nicht unterschiedlich stark beschleunigt sind).
tags: Universum1gegreit Geschwindigkeit1gegreit SRT1gegreit
 Nach oben
Nach oben