Relativitätstheorie: Einsteins Feldgleichung
|
|
D i s k u s s i o n
Beitrag 0-89
Leben wir in einer Welt gebrochener Supersymmetrie?
Sind supersymmetrische Ansätze der Teilchenphysik
sinnvoller als nur eichsymmetrische?
Unter einer Eichtheorie versteht man eine physikalische Feldtheorie, die einer lokalen Eichsymmetrie genügt (was bedeutet, dass die von der Theorie vorhergesagten Wechselwirkungen sich nicht ändern, wenn eine bestimmte Größe lokal frei gewählt wird).
In der Quantenmechanik etwa werden Teilchen nicht mehr durch Ort und Impuls, sondern durch die sogenannte Wellenfunktion ψ(x,t) beschrieben. Sie ist ein Feld, also eine — i.A. komplexwertige — Funktion von Raum und Zeit. Eindeutig aber ist sie keineswegs, denn
für jedes reele φ beschreiben ψ(x,t) und eiφ ψ(x,t) denselben Zustand.
Es handelt sich hier um eine globale Symmetrie ( mathematisch gegeben durch die Lie-Gruppe U(1), denn die besteht gerade aus allen komplexen Zahlen eiφ ).
Das Problem mit den Eichtheorien ist, dass sie
Zudem gibt es unendlich viele mögliche Eichtheorien, und diejenigen, die man auswählt, die Wechselwirkungen der Physik zu beschreiben, müssen ad hoc zurechtgestutzt werden, damit sie mit den Beobachtungen der realen Welt übereinstimmen. Schlimmer noch: Die Eichtheorien sagen nichs darüber aus, wie viele verschiedene Arten von Teilchen es geben sollte.
Die Physiker würden statt der Eichtheorien gerne eine eindeutige Theorie haben, die klar dazu Stellung nimmt, wie viele Teilchenarten es gibt. Ein Schritt hin zu einer Theorie mit diesen Eigenschaften wurde 1974 mit der Erfindung der sog. Supersymmetrie getan. Ausgangspunkt war die Frage, wie eine vollkommen symmetrische Welt beschaffen sein müsse, in der jedem Fermion ein Boson mit gleicher Masse entsprechen würde.
In der Natur beobachten wir solche Symmetrie nicht, aber das könnte man damit erklären, dass die Symmetrie gebrochen wurde wie im Fall der elektroschwachen Wechselwirkung. Brechung der Symmetrie tritt immer dann ein, wenn der symmetrische Zustand instabil, der gebrochen symmetrische aber stabil ist:

Quelle: Crashkurs in Quantenmechanik
Die gezeigte Situation wäre symmetrischer, wenn die Kugel auf der Bergspitze läge — die Lage aber ist nicht stabil.
Mathematisch ergeben sich Möglichkeiten, Supersymmetrien zu beschreiben, die möglicherweise zu Beginn des Urknalls bestanden, dann aber gebrochen wurden mit dem Effekt, dass die uns bekannten Teilchen kleiner Masse entstanden, während ihre Superpartner — Teilchen mit sehr großer Masse — sich schon bald in einen Schauer leichterer Teilchen aufgelöst haben.
Um heute Superteilchen zu erzeugen müssten wir Bedingungen schaffen wie zu Beginn des Urknalls. Die dazu notwendigen hohen Energien aber lassen sich heute selbst im CERN noch bei weitem nicht erzeugen. Man bräuchte dazu Teilchenbeschleuniger von mindestens der Größe unseres Sonnensystems.
Man sieht: Das alles ist noch mit sehr viel WENN und ABER versehen, weist aber doch einen großen Pluspunkt auf:
Es gibt verschiedene Spielarten einer supersymmetrischen Feldtheorie. Sie alle variieren das Thema durch Einschränkungen der Symmetrie, was ur Folge hat, dassvso eine Theorie dann auch nur eine begrenzte Anzahl verschiedener Teilchenarten zulässt: Einge Versionen enthalten hunderte, doch andere lassen sehr viel weniger zu, und keine der Theorien sagt voraus, dass die Zahl der fundamentalen Teilchen unendlich sein könnte.
Das beste aber ist: Supersymmetrische Theorien kommen ohne Renormierung aus, erfordern also keine Verletzung von Regeln der Mathematik.
Das wäre gut, aber die Physiker wissen, dass da noch etwas fehlt — sie wissen nur nicht was.
Verschiedene supersymmetrische Theorien stimmem recht gut mit den verschiedenen Erscheinungen der realen Welt überein, aber keine erklärt alles.
Die Problem sind immens, doch für supersymmetrische Theorien spricht mindestens, dass sie widerspruchsfrei sind und endlich und keinerlei Renormalisierung bedürfen. Sie vermitteln den Physikern das Gefühl, mit ihnen auf der rechten Spur zu sein.
Wie aber kann es je gelingen, sie zu überprüfen?
Dieses Punktes wegen nimmt die Kosmologie, die ja das gesamte Universum zu erforschen sucht, heute solch gewaltigen Aufschwung. Heinz Pagels — geschäftsführender Direktor der New Yorker Akademie der Wissenschaften — sage 1983 (Zitat): Wir sind bereits in die Ära der Physik nach dem Beschleuniger eingetreten. Für sie wird die gesamte Geschichte des Universums zum Prüfstand der fundamentalen Physik.
Uns so widmen sich die Kosmologen heute mit nicht geringem Eifer auch der Teilchenphysik ...
Quelle: John Gribbin: Auf der Suche nach Schrödingers Katze — Quantenphysik
und Wirklichkeit, Piper 2004, S. 282-286.
Was Supersymmetrie (SUSY) wahrscheinlich macht
Warum man sich heute vor allem auf supersymmetrische Varianten der Stringtheorie konzentriert — warum man also glaubt, die Physik unserer Welt müsse supersymmetrisch sein —, liegt vor allem daran, dass man nachrechnen konnte, dass die Kopplungskonstanten der starken Wechselwirking (rot), der schwachen Wechselwirkung (grün) und der elektromagnetischen Kraft (violett) mit steigender Energie nur dann konvergieren, wenn Supersymmetrie gegeben ist:
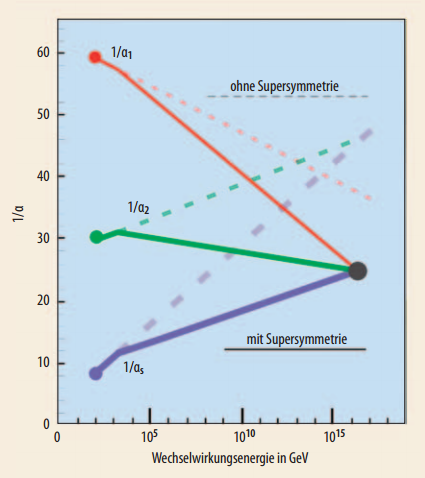
Quelle: DESY
Supersymmetrische Teilchen haben sich bisher hartnäckig ihrer Entdeckung entzogen. Es stellt sich daher die Frage, ab welchem Zeitpunkt die experimentellen Fakten so stark gegen SUSY sprechen, dass man sich trotz all ihrer Vorzüge nach etwas anderem umschauen muss.
Wann also kann man sagen, dass SUSY (Supersymmetrie) falsifiziert wurde? Diese Frage ist nicht leicht zu beantworten, da SUSY eine gebrochene Symmetrie sein muss (ansonsten hätten die Superpartner die gleichen Massen wie die Teilchen des Standardmodells und wären schon lange beobachtet worden). Wie der Übergang von voller zu gebrochener SUSY vor sich gegangen sein könnte, ist noch unverstanden.
Verzichtet man in der Stringtheorie auf Supersymmetrie, so sagt sie Tachyonen voraus (Teilchen, die sich grundsätzlich nur schneller als Licht bewegen). Erst die Superstringtheorie garantiert, dass keine Tachyonen involviert sind und gewährleistet die Erhaltung des wertvollen und bisher immer verifizierten Kausalitätsprinzips ('Ursache kommt vor der Wirkung').
sinnvoller als nur eichsymmetrische?
Unter einer Eichtheorie versteht man eine physikalische Feldtheorie, die einer lokalen Eichsymmetrie genügt (was bedeutet, dass die von der Theorie vorhergesagten Wechselwirkungen sich nicht ändern, wenn eine bestimmte Größe lokal frei gewählt wird).
In der Quantenmechanik etwa werden Teilchen nicht mehr durch Ort und Impuls, sondern durch die sogenannte Wellenfunktion ψ(x,t) beschrieben. Sie ist ein Feld, also eine — i.A. komplexwertige — Funktion von Raum und Zeit. Eindeutig aber ist sie keineswegs, denn
Es handelt sich hier um eine globale Symmetrie ( mathematisch gegeben durch die Lie-Gruppe U(1), denn die besteht gerade aus allen komplexen Zahlen eiφ ).
Das Problem mit den Eichtheorien ist, dass sie
- nicht eindeutig sind
- und auf unendlich große Zwischenergebnisse führen, die durch Renormierung zurechtgestutzt werden müssen, damit die Theorie der Realität entsprechende Aussagen macht.
Zudem gibt es unendlich viele mögliche Eichtheorien, und diejenigen, die man auswählt, die Wechselwirkungen der Physik zu beschreiben, müssen ad hoc zurechtgestutzt werden, damit sie mit den Beobachtungen der realen Welt übereinstimmen. Schlimmer noch: Die Eichtheorien sagen nichs darüber aus, wie viele verschiedene Arten von Teilchen es geben sollte.
Die Physiker würden statt der Eichtheorien gerne eine eindeutige Theorie haben, die klar dazu Stellung nimmt, wie viele Teilchenarten es gibt. Ein Schritt hin zu einer Theorie mit diesen Eigenschaften wurde 1974 mit der Erfindung der sog. Supersymmetrie getan. Ausgangspunkt war die Frage, wie eine vollkommen symmetrische Welt beschaffen sein müsse, in der jedem Fermion ein Boson mit gleicher Masse entsprechen würde.
In der Natur beobachten wir solche Symmetrie nicht, aber das könnte man damit erklären, dass die Symmetrie gebrochen wurde wie im Fall der elektroschwachen Wechselwirkung. Brechung der Symmetrie tritt immer dann ein, wenn der symmetrische Zustand instabil, der gebrochen symmetrische aber stabil ist:

Quelle: Crashkurs in Quantenmechanik
Die gezeigte Situation wäre symmetrischer, wenn die Kugel auf der Bergspitze läge — die Lage aber ist nicht stabil.
Mathematisch ergeben sich Möglichkeiten, Supersymmetrien zu beschreiben, die möglicherweise zu Beginn des Urknalls bestanden, dann aber gebrochen wurden mit dem Effekt, dass die uns bekannten Teilchen kleiner Masse entstanden, während ihre Superpartner — Teilchen mit sehr großer Masse — sich schon bald in einen Schauer leichterer Teilchen aufgelöst haben.
Um heute Superteilchen zu erzeugen müssten wir Bedingungen schaffen wie zu Beginn des Urknalls. Die dazu notwendigen hohen Energien aber lassen sich heute selbst im CERN noch bei weitem nicht erzeugen. Man bräuchte dazu Teilchenbeschleuniger von mindestens der Größe unseres Sonnensystems.
Man sieht: Das alles ist noch mit sehr viel WENN und ABER versehen, weist aber doch einen großen Pluspunkt auf:
Es gibt verschiedene Spielarten einer supersymmetrischen Feldtheorie. Sie alle variieren das Thema durch Einschränkungen der Symmetrie, was ur Folge hat, dassvso eine Theorie dann auch nur eine begrenzte Anzahl verschiedener Teilchenarten zulässt: Einge Versionen enthalten hunderte, doch andere lassen sehr viel weniger zu, und keine der Theorien sagt voraus, dass die Zahl der fundamentalen Teilchen unendlich sein könnte.
Das beste aber ist: Supersymmetrische Theorien kommen ohne Renormierung aus, erfordern also keine Verletzung von Regeln der Mathematik.
Das wäre gut, aber die Physiker wissen, dass da noch etwas fehlt — sie wissen nur nicht was.
Verschiedene supersymmetrische Theorien stimmem recht gut mit den verschiedenen Erscheinungen der realen Welt überein, aber keine erklärt alles.
- Besondere Erwähnung verdient eine, die man die N = 8 Superschwerkraft nennt:
- 8 weiteren Teilchen (daher N = 8), die man Gravitinos nennt,
- 56 Materieteilchen (vor allem Quarks und Elektronen)
- sowie 98 weiteren Teilchen, die nicht-gravitative Wechselwirkung vermitteln (Photonen, Gluonen und andere Bosonen)
Ihr liegt ein hypothetisches Boson zugrunde, das Graviton, welches die gravitative Wechselwirkung vermittelt.
Es wird begleitet von
Das ist eine große Menge verschiedener Teilchen, aber die Theorie sagt sie voraus und lässt keine weiteren zu.
Wie energiereich die Gravitinos seien, sagt die Theorie nicht. Es könnte sich um geisterhafte Teilchen mit extrem wenig Masse handeln, die praktisch nie mit irgend etwas wechselwirken. Andererseits könnten sie aber auch extrem massereich sein, so dass Menschen wohl nie werden Beschleuniger bauen können, die hinreichend viel Energie bereitstellen, sie zu erzeugen und zu beobachten.
Die Problem sind immens, doch für supersymmetrische Theorien spricht mindestens, dass sie widerspruchsfrei sind und endlich und keinerlei Renormalisierung bedürfen. Sie vermitteln den Physikern das Gefühl, mit ihnen auf der rechten Spur zu sein.
Wie aber kann es je gelingen, sie zu überprüfen?
Dieses Punktes wegen nimmt die Kosmologie, die ja das gesamte Universum zu erforschen sucht, heute solch gewaltigen Aufschwung. Heinz Pagels — geschäftsführender Direktor der New Yorker Akademie der Wissenschaften — sage 1983 (Zitat): Wir sind bereits in die Ära der Physik nach dem Beschleuniger eingetreten. Für sie wird die gesamte Geschichte des Universums zum Prüfstand der fundamentalen Physik.
Uns so widmen sich die Kosmologen heute mit nicht geringem Eifer auch der Teilchenphysik ...
Warum man sich heute vor allem auf supersymmetrische Varianten der Stringtheorie konzentriert — warum man also glaubt, die Physik unserer Welt müsse supersymmetrisch sein —, liegt vor allem daran, dass man nachrechnen konnte, dass die Kopplungskonstanten der starken Wechselwirking (rot), der schwachen Wechselwirkung (grün) und der elektromagnetischen Kraft (violett) mit steigender Energie nur dann konvergieren, wenn Supersymmetrie gegeben ist:

Quelle: DESY
Supersymmetrische Teilchen haben sich bisher hartnäckig ihrer Entdeckung entzogen. Es stellt sich daher die Frage, ab welchem Zeitpunkt die experimentellen Fakten so stark gegen SUSY sprechen, dass man sich trotz all ihrer Vorzüge nach etwas anderem umschauen muss.
Wann also kann man sagen, dass SUSY (Supersymmetrie) falsifiziert wurde? Diese Frage ist nicht leicht zu beantworten, da SUSY eine gebrochene Symmetrie sein muss (ansonsten hätten die Superpartner die gleichen Massen wie die Teilchen des Standardmodells und wären schon lange beobachtet worden). Wie der Übergang von voller zu gebrochener SUSY vor sich gegangen sein könnte, ist noch unverstanden.
Verzichtet man in der Stringtheorie auf Supersymmetrie, so sagt sie Tachyonen voraus (Teilchen, die sich grundsätzlich nur schneller als Licht bewegen). Erst die Superstringtheorie garantiert, dass keine Tachyonen involviert sind und gewährleistet die Erhaltung des wertvollen und bisher immer verifizierten Kausalitätsprinzips ('Ursache kommt vor der Wirkung').
Beitrag 0-132
Supersymmetrie und die GUT (Grand Unified Theory) vereinigen 3 Kopplungskonstanten
Supersymmetrie und die GUT
Die Idee der Supersymmetrie (SUSY) hat mehrere Wurzeln:
Ihr heutiges Gewicht erlangte SUSY, als
Erst der Schwarz und Green 1984 gelungene Nachweis, dass die Stringtheorie — da supersymmetrisch — frei von Anomalien und Unendlichkeiten ist, hat die Stringtheorie von einem Außenseiter zum einem ebenso zentralen Thema wie SUSY gemacht.
Noch lange bevor die Idee der Supersymmetrie als möglicherweise brauchbar anerkannt war, sind Howard Georgi und Sheldon Glashow auf die Vermutung gestoßen, dass die starke und die elektroschwache Kraft unterschiedliche Facetten einer einzigen Kraft sein könnten.
Ihr Vorschlag ist heute bekannt als Grand Unified Theory (GUT).
Das Standardmodell hingegen beschreibt die starke, die schwache und die elektromagnetische Kraft durch eine Eichsymmetrie, die sich in 3 Lie-Gruppen ausdrückt und somit 3 Kopplungskonstanten hat. Sie bestimmen die Stärke der jeweiligen Kraft und lassen sich recht genau durch Messung bestimmen.
Wie aber soll dann die GUT — und damit eine einzige Kopplungskonstante — alle drei Kräfte beschreiben können, wo sie doch unterschiedliche Stärke haben?
Die Antwort darauf versteckt sich im Vorhandensein virtueller Teilchen:
Betrachten wir zunächst nur die elektromagnetische Kraft. Der klassischen Physik zufolge übet ein elektrisch geladenes Objekt — eine Elektron etwa — eine Kraft aus, die sich mit dem Quadrat der Entfernung vom Objekt verringert. Nun lehrt uns die Quantenmechanik aber, dass der Raum ständig und überall mit Wolken virtueller Teilchen durchsetzt ist. Das Elektron stößt sie ab bzw. zieht sie an, je nachdem, ob sie negativ oder positive Ladung tragen.
Damit ist die Stärke der Ladung des Elektrons — aus gewisser Entfernung gesehen — reduziert durch einen Schwarm positive geladener, zum Elektron hin gezogener virtueller Teilchen. Näherd man sich dann aber dem Elektron, so verschwindet diese Wirkung zusehens, da zwischen uns und dem Elektron dann zunehmend weniger solcher Teilchen sein werden.
Dieser Effekt lässt sich vergleichen mit dem Licht einer Straßenlaterne, das im Nebel vor uns auftaucht: Wir werden sie umso klarer erkennen, je näher wir ihr kommen (weil dann zwischen ihr und uns weniger Nebel sein wird, der Licht verschluckt).
Wir sehen also:
Auch die Kopplungskonstante der QCD hängt von der Entfernung ab. Hier aber wächst sie mit zunehmender Entfernung, da virtuelle Gluonen die Farbladungen verstärken, nicht aber abschirmen. [Für die Entdeckung dieser Abhängigkeit erhielten Gross, Politzer und Wilczek 2004 den Nobelpreis.]
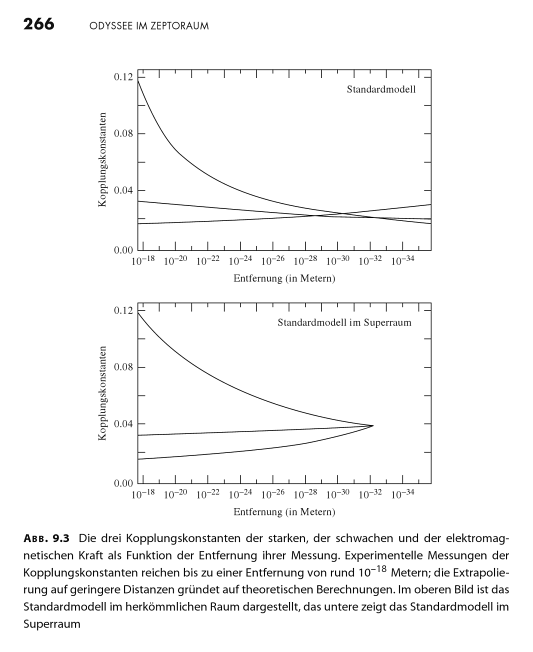
Quelle: Giudice: Odyssee im Zeptoraum, Springer 2012
Noch bei einem Abstand von 2 Nanometern lassen sich alle 3 Kopplungskonstanten gut messen. Rechnet man das Ergebnis solcher Beobachtung um auf Entfernungen von nur noch 10-32 Metern, kommt es fast schon zu einer Übereinstimmung aller 3 Konstanten.
Die eigentliche Überraschung aber:
Führt man jene Berechnung auch unter der Annahme von Supersymmetrie durch,
so ergibt sich — im Rahmen experimenteller Fehlergrenzen — tatsächlich für alle 3 Konstanten derselbe Wert.
Dies also ist der Grund dafür, dass man heute vermutet, unsere Welt sei supersymmetrisch.
Der Beweis hierfür — so denkt man heute — könnte sich noch mit dem LHC im CERN finden lassen, denn wie andere Überlegungen (s.u.) zeigen, sollten die Superpartner der uns inzwischen bekannten Teilchen jeweils nicht mehr als etwa 1 TeV Energie tragen.
Begründen lässt sich das so: Jedes der beiden Teilchen, die ein Superpaar bilden, trägt viel zur Dichte der Higgs-Substanz bei. Beider Beiträge sind exakt gleich, haben entgegengesetztes Vorzeichen und sollten einander daher aufheben. Wer die Berechnung ein erstes Mal durchführt, dem erscheint diese vollkommene Aufhebung großer Beiträge wie ein großes Wunder.
Zufall aber ist das keineswegs — denn was sich hier manifestiert ist die Macht gegebener Symmetrien: Die Higgs-Substanz — im gewöhnlichen Raum durch virtuelle Teilchen gestört — bleibt im Superraum vollkommen unberührt.
In Wirklichkeit aber kommt es der Anwesenheit virtueller Teilchen wegen zu einer spontanen Brechung dieser Symmetrie, so dass die Aufhebung der durch die beiden Superpartner produzierten Beiträge nur noch grob gegeben ist. Unter der Voraussetzung, dass der verbleibende Effekt nicht wieder ein Natürlichkeitsproblem zur Folge hat, kommt man zum Schluss, dass die Massen der erwarteten Superpartner auf etwa 1 TeV begrenzt sein sollten.
Nebenbei noch:
SUSY wird nicht nur im Rahmen der Stringtheorie betrachtet, sondern ist heute auch eine schon vollständig spezifizierte Erweiterung des Standardmodells der Elementarteilchen. Doch der Preis dafür ist hoch: Eine enorme Menge freier, d.h. nur durch Messung bestimmbarer Parameter.
Rüdiger Vaas nennt 12 Varianten der SUSY-Theorie, die jeweils unterschiedlich viel freie Parameter haben (zwischen 3 und 105).
Im Rahmen des Standardmodells sind nur Protonen, Elektronen und Neutrinos völlig stabile Teilchen (wobei sich Elektronen und Neutrinos aber in einander umwandeln können). Alle andere Teilchen zerfallen, wenn frei, in Sekundenbruchteilen — abgesehen von freien Neutronen, deren Lebensdauer knapp 15 Min beträgt.
Auch GUT existiert als Theorie in mehreren Varianten:
Ende der 80-er Jahre begann das Interesse an den GUT-Theorien nachzulassen — nicht zuletzt deswegen, weil jede von ihnen eine bestimmte (wenn auch das Alter unseres Universums um etwa 20 Größenordnungen übersteigende) mittlere Zerfallszeit für Protonen voraussagt, bisher aber noch kein einziger Protonenzerfall beobachtet werden konnte — und das, obgleich es eine ganze Reihe von Detektoren gibt, in denen nach Anzeichen dafür gesucht wird.
GUT widerspricht dem Standardmodell der Elementarteilchenphysik, denn ihm zufolge kann es keinen Protonenzerfall geben, da er den Erhaltungssatz für die Baryonenanzahl verletzen würde.

Die Idee der Supersymmetrie (SUSY) hat mehrere Wurzeln:
- Julius Wess und Bruno Zumino erfanden sie als Vermutung,
- Neveu und Schwarz — sowie unabhängig von ihnen Pierre Ramond — haben sie 1971 in der Stringtheorie entdeckt.
Ihr heutiges Gewicht erlangte SUSY, als
- 1976 Scherk, Gliozzi und Olive zeigen konnten, dass supersymmetrische Stringtheorie frei von bestimmten Unendlichkeiten ist und
- 1981 Schwarz und Green einen Beweis dafür fanden, dass die gesamte Stringtheorie supersymmetrisch ist (dies zu betonen spricht man heute von Superstrings und Superstringtheorie).
Erst der Schwarz und Green 1984 gelungene Nachweis, dass die Stringtheorie — da supersymmetrisch — frei von Anomalien und Unendlichkeiten ist, hat die Stringtheorie von einem Außenseiter zum einem ebenso zentralen Thema wie SUSY gemacht.
Noch lange bevor die Idee der Supersymmetrie als möglicherweise brauchbar anerkannt war, sind Howard Georgi und Sheldon Glashow auf die Vermutung gestoßen, dass die starke und die elektroschwache Kraft unterschiedliche Facetten einer einzigen Kraft sein könnten.
Ihr Vorschlag ist heute bekannt als Grand Unified Theory (GUT).
Das Standardmodell hingegen beschreibt die starke, die schwache und die elektromagnetische Kraft durch eine Eichsymmetrie, die sich in 3 Lie-Gruppen ausdrückt und somit 3 Kopplungskonstanten hat. Sie bestimmen die Stärke der jeweiligen Kraft und lassen sich recht genau durch Messung bestimmen.
Wie aber soll dann die GUT — und damit eine einzige Kopplungskonstante — alle drei Kräfte beschreiben können, wo sie doch unterschiedliche Stärke haben?
Die Antwort darauf versteckt sich im Vorhandensein virtueller Teilchen:
Betrachten wir zunächst nur die elektromagnetische Kraft. Der klassischen Physik zufolge übet ein elektrisch geladenes Objekt — eine Elektron etwa — eine Kraft aus, die sich mit dem Quadrat der Entfernung vom Objekt verringert. Nun lehrt uns die Quantenmechanik aber, dass der Raum ständig und überall mit Wolken virtueller Teilchen durchsetzt ist. Das Elektron stößt sie ab bzw. zieht sie an, je nachdem, ob sie negativ oder positive Ladung tragen.
Damit ist die Stärke der Ladung des Elektrons — aus gewisser Entfernung gesehen — reduziert durch einen Schwarm positive geladener, zum Elektron hin gezogener virtueller Teilchen. Näherd man sich dann aber dem Elektron, so verschwindet diese Wirkung zusehens, da zwischen uns und dem Elektron dann zunehmend weniger solcher Teilchen sein werden.
Dieser Effekt lässt sich vergleichen mit dem Licht einer Straßenlaterne, das im Nebel vor uns auftaucht: Wir werden sie umso klarer erkennen, je näher wir ihr kommen (weil dann zwischen ihr und uns weniger Nebel sein wird, der Licht verschluckt).
Wir sehen also:
- In der klassischen Physik hängt zwar die Stärke der elektromagnetischen Kraft von der Entfernung ab, nicht aber die Ladung des Objekts.
- Anders in der Quantenmechanik: Hier nehmen wir die Ladung als entfernungsabhängig wahr.
Auch die Kopplungskonstante der QCD hängt von der Entfernung ab. Hier aber wächst sie mit zunehmender Entfernung, da virtuelle Gluonen die Farbladungen verstärken, nicht aber abschirmen. [Für die Entdeckung dieser Abhängigkeit erhielten Gross, Politzer und Wilczek 2004 den Nobelpreis.]

Quelle: Giudice: Odyssee im Zeptoraum, Springer 2012
Noch bei einem Abstand von 2 Nanometern lassen sich alle 3 Kopplungskonstanten gut messen. Rechnet man das Ergebnis solcher Beobachtung um auf Entfernungen von nur noch 10-32 Metern, kommt es fast schon zu einer Übereinstimmung aller 3 Konstanten.
Die eigentliche Überraschung aber:
so ergibt sich — im Rahmen experimenteller Fehlergrenzen — tatsächlich für alle 3 Konstanten derselbe Wert.
Dies also ist der Grund dafür, dass man heute vermutet, unsere Welt sei supersymmetrisch.
Der Beweis hierfür — so denkt man heute — könnte sich noch mit dem LHC im CERN finden lassen, denn wie andere Überlegungen (s.u.) zeigen, sollten die Superpartner der uns inzwischen bekannten Teilchen jeweils nicht mehr als etwa 1 TeV Energie tragen.
Begründen lässt sich das so: Jedes der beiden Teilchen, die ein Superpaar bilden, trägt viel zur Dichte der Higgs-Substanz bei. Beider Beiträge sind exakt gleich, haben entgegengesetztes Vorzeichen und sollten einander daher aufheben. Wer die Berechnung ein erstes Mal durchführt, dem erscheint diese vollkommene Aufhebung großer Beiträge wie ein großes Wunder.
Zufall aber ist das keineswegs — denn was sich hier manifestiert ist die Macht gegebener Symmetrien: Die Higgs-Substanz — im gewöhnlichen Raum durch virtuelle Teilchen gestört — bleibt im Superraum vollkommen unberührt.
In Wirklichkeit aber kommt es der Anwesenheit virtueller Teilchen wegen zu einer spontanen Brechung dieser Symmetrie, so dass die Aufhebung der durch die beiden Superpartner produzierten Beiträge nur noch grob gegeben ist. Unter der Voraussetzung, dass der verbleibende Effekt nicht wieder ein Natürlichkeitsproblem zur Folge hat, kommt man zum Schluss, dass die Massen der erwarteten Superpartner auf etwa 1 TeV begrenzt sein sollten.
Nebenbei noch:
SUSY wird nicht nur im Rahmen der Stringtheorie betrachtet, sondern ist heute auch eine schon vollständig spezifizierte Erweiterung des Standardmodells der Elementarteilchen. Doch der Preis dafür ist hoch: Eine enorme Menge freier, d.h. nur durch Messung bestimmbarer Parameter.
Rüdiger Vaas nennt 12 Varianten der SUSY-Theorie, die jeweils unterschiedlich viel freie Parameter haben (zwischen 3 und 105).
- Eine davon — CMSSM — gilt schon fast als widerlegt, da sie durch Zwangsbedingungen stark simplifiziert ist, deren Parameterraum sich als Ergebnis von Messungen am LHC schon als nahezu leer erwiesen hat.
Im Rahmen des Standardmodells sind nur Protonen, Elektronen und Neutrinos völlig stabile Teilchen (wobei sich Elektronen und Neutrinos aber in einander umwandeln können). Alle andere Teilchen zerfallen, wenn frei, in Sekundenbruchteilen — abgesehen von freien Neutronen, deren Lebensdauer knapp 15 Min beträgt.
Auch GUT existiert als Theorie in mehreren Varianten:
- Die einfachste davon — mit Symmetriegruppe SU(5) — würde erst durch SUSY so ergänzt, dass die Kehrwerte der Kopplungsstärken der
schwachen, der starken und der elektromagnetischen Kraft ab etwa 1016 GeV gleich sind.
Eben diese GUT-Variante aber gerät derzeit in Bedrängnis, da sie bisher nicht entdeckten Protonenzerfall voraussagt. Im übrigen sind die im Bild gezeigten Kurven für die Entwicklung der Kopplungsstärken in zunehmend höhere Energiebereiche hinein schon ab etwa 200 GeV extrapoliert (!).
- In anderen GUT-Modellen — darunter einem mit Symmetriegruppe SO(10) — konvergiert die Stärke der Kräfte auch ohne SUSY.
- All das zeigt, dass SUSY — dann aber auch die Stringtheorie — sich durchaus noch als Irrweg erweisen könnten.
Ende der 80-er Jahre begann das Interesse an den GUT-Theorien nachzulassen — nicht zuletzt deswegen, weil jede von ihnen eine bestimmte (wenn auch das Alter unseres Universums um etwa 20 Größenordnungen übersteigende) mittlere Zerfallszeit für Protonen voraussagt, bisher aber noch kein einziger Protonenzerfall beobachtet werden konnte — und das, obgleich es eine ganze Reihe von Detektoren gibt, in denen nach Anzeichen dafür gesucht wird.
GUT widerspricht dem Standardmodell der Elementarteilchenphysik, denn ihm zufolge kann es keinen Protonenzerfall geben, da er den Erhaltungssatz für die Baryonenanzahl verletzen würde.

Beitrag 0-330
Magnetische Monopole — gibt es sie?
Magnetische Monopole — gibt es sie?
Die GUT-Theorien sagen die Existenz magnetischer Monopole voraus, d.h. die Existenz von Elementarteilchen, deren jedes einen einzelnen magnetischen Nord- oder Südpol darstellt.
Warum aber hat man solche Teilchen bisher nicht gefunden?
Alan Guth — nachdem er 1979 die Inflationstheorie vorschlug — hat sich mit dieser Frage eingehend befasst und glaubt errechnet zu haben, dass derartige Teilchen nur entstehen können bei Temperaturen, wie sie in unserem Universum schon kurz nach Beginn der Inflationsphase nicht mehr geherrscht haben.
Da der durch Menschen einsehbare Teil des Weltalls damals aber extrem kleinen Durchmesser hatte — wohl kleiner als die Plancklänge —, sein nicht wahrscheinlich, dass er damals mehr als nur ganz wenige magnetische Monopole enthalten haben kann. Sie könnten heute durchaus noch existieren, wären dann aber in unserem Universum extrem selten, da nun ja über einen kugelförmigen Bereich verteilt, dessen Radius ca. 43 Mrd. Lichtjahre beträgt.
Wir dürfen deswegen nicht erwarten, auch nur ein oder zwei davon wirklich zu finden.
Die GUT-Theorien sagen die Existenz magnetischer Monopole voraus, d.h. die Existenz von Elementarteilchen, deren jedes einen einzelnen magnetischen Nord- oder Südpol darstellt.
Warum aber hat man solche Teilchen bisher nicht gefunden?
Alan Guth — nachdem er 1979 die Inflationstheorie vorschlug — hat sich mit dieser Frage eingehend befasst und glaubt errechnet zu haben, dass derartige Teilchen nur entstehen können bei Temperaturen, wie sie in unserem Universum schon kurz nach Beginn der Inflationsphase nicht mehr geherrscht haben.
Da der durch Menschen einsehbare Teil des Weltalls damals aber extrem kleinen Durchmesser hatte — wohl kleiner als die Plancklänge —, sein nicht wahrscheinlich, dass er damals mehr als nur ganz wenige magnetische Monopole enthalten haben kann. Sie könnten heute durchaus noch existieren, wären dann aber in unserem Universum extrem selten, da nun ja über einen kugelförmigen Bereich verteilt, dessen Radius ca. 43 Mrd. Lichtjahre beträgt.
Wir dürfen deswegen nicht erwarten, auch nur ein oder zwei davon wirklich zu finden.
Beitrag 0-139
Eichsymmetrie und seine Basis: Das Noethersche Theorem
Das Noethersche Theorem
Emmi Noether — eine ganz herausragende Mathematikerin — hat entdeckt, dass jede nicht diskrete (d.h. fließende, also kontinuierliche) Symmetrie einer physikalischen Theorie einen Erhaltungssatz zur Folge hat.
Ihr Theorem sagt z.B.
Noethers Entdeckung dieser Zusammenhänge hilft bei der Entwicklung von Theorien:
Wo Experimente darauf hindeuten, dass es für eine Größe einen Erhaltungssatz geben könnte, kann man das als Hinweis darauf deuten, dass in der Theorie eine Symmetrie zu finden sein sollte (auch wenn zunächst nicht klar ist, welche das sein könnte).
In der Physik — und auch in Noethers Theorem — ist mit einer Symmetrie nicht notwendig eine geometrischer Art gemeint:
Ein symmetrisches Modell ist dort eines, welches
Erstes Beispiel einer eichinvarianten Theorie war die Maxwellsche Theorie der Elektrodynamik:
Mit den Eichfeldern hat man sozusagen grundlegendere Felder eingeführt, die nicht direkt messbar sind und durch eine Eichtransformation umdefiniert werden können ohne dass der physikalische Gehalt sich ändert. [Hohnerkamp, 2015]
Man könnte nun denken, dass solche Hintergrundfelder einzuführen und ihre Symmetrie (Eichinvarianz) zu betrachten, künstlich und überflüssig ist.
Dennoch erwies eben diese Idee sich als Schlüssel zur Formulierung der sog. Quantenelektrodynamik (QED).
Und nicht nur das: Sie wies auch den Weg zur verallgemeinerten Quantenfeldtheorie der elektroschwachen Theorie und schließlich der heutigen Standardtheorie zur Beschreibung der starken, der schwachen und der elektromagnetischen Wechselwirkung — der Grand Unified Theory (GUT).
Während in der QED das Eichfeld für ein Photon steht, beschreiben die Eichfelder der allgemeineren Standardtheorie auch die Austauschteilchen der starken und schwachen Wechselwirkung. Hier also sind die Eichfelder keine Hilfsfelder mehr wie in der klassischen Elektrodynamik, sondern die Bosonen selbst.
Wir sehen:
Es war die Idee der Eichsymmetrie,
die letztlich zur gelungenen Vereinheitlichung von nun schon 3 der insgesamt 4 physikalischen Grundkräfte geführt hat.
Selbst in der Allgemeinen Relativitätstheorie — für die es bisher ja noch keine Quantenversion gibt — findet sich das Eichprinzip verwirklicht: Das Eichfeld ist dort die Metrik, und die Eichtransformationen sich die allgemeinen Koordinatentransformationen. [Hohnerkamp, 2015]
Quelle: Josef Honerkamp:
Wissenschaft und Weltbilder, Springer 2015, S. 228-233
Nach Wolfgang Osterhage (Seite 154) besteht die Eininvarianz darin, dass man den Potential-Nullpunkt frei wählen (ihn "eichen") kann, ohne dass das Einfluss auf physikalische Vorgänge hat.
Er sagt auch, dass die Erhaltungssätze für Leptonen- und Baryonenzahl mit Quantensymmetrien verknüpft seien und es über die bisher hier genannten Symmetrien für Zeit und Raum nur noch eine weitere geben könne: die Supersymmetrie. Sie beeinflusst den Spinwert — erhöht oder erniedrigt ihn um 1/2 —, macht also aus Fermionen Bosonen und aus Bosonen Fermionen.
Über die vier oben schon erwähnten Erhaltungssätze hinaus — die für Energie, Impuls, Drehimpils und Ladungsdichte — gibt es noch zwei weitere:
Neben den fließenden, also kontinuierlichen Symmetrien gibt es weitere, die diskret sind. Es sind dies
Auch jede Kombination von ihnen erhält — fast immer — das Verhalten des betrachteten Systems. Seltsamerweise aber gibt es da Ausnahmen: Bestimmte Prozesse, in denen die s c h w a c h e Wechselwirkung eine Rolle spielt, verletzen C, P oder CP.
Emmi Noether — eine ganz herausragende Mathematikerin — hat entdeckt, dass jede nicht diskrete (d.h. fließende, also kontinuierliche) Symmetrie einer physikalischen Theorie einen Erhaltungssatz zur Folge hat.
Ihr Theorem sagt z.B.
- Invarianz gegenüber jeder Verschiebung der Zeitkoordinate impliziert den Energie-Erhaltungssatz.
- Invarianz gegenüber jeder Verschiebung der Raumkoordinaten impliziert den Impuls-Erhaltungssatz.
- Invarianz gegenüber Drehungen im Raum impliziert den Drehimpuls-Erhaltungssatz.
Noethers Entdeckung dieser Zusammenhänge hilft bei der Entwicklung von Theorien:
Wo Experimente darauf hindeuten, dass es für eine Größe einen Erhaltungssatz geben könnte, kann man das als Hinweis darauf deuten, dass in der Theorie eine Symmetrie zu finden sein sollte (auch wenn zunächst nicht klar ist, welche das sein könnte).
In der Physik — und auch in Noethers Theorem — ist mit einer Symmetrie nicht notwendig eine geometrischer Art gemeint:
Ein symmetrisches Modell ist dort eines, welches
- unter einer gewissen Menge von Transformationen seiner selbst invariant ist
- und diese Menge von Transformationen sich als Gruppe im mathematischen Sinne darstellt.
Erstes Beispiel einer eichinvarianten Theorie war die Maxwellsche Theorie der Elektrodynamik:
-
Es werden dort sog. Eichfelder transformiert, und die Invarianz besteht darin, dass die messbaren Felder — das elektrische und das magnetische Feld —
durch die Transformation sich nicht ändern, obgleich sie sich aus den Eichfeldern — das sind hier elektromagnetische Potentiale — berechnen lassen.
Diese Symmetrie impliziert den Erhaltungssatz für elektrische Ladung.
Mit den Eichfeldern hat man sozusagen grundlegendere Felder eingeführt, die nicht direkt messbar sind und durch eine Eichtransformation umdefiniert werden können ohne dass der physikalische Gehalt sich ändert. [Hohnerkamp, 2015]
Man könnte nun denken, dass solche Hintergrundfelder einzuführen und ihre Symmetrie (Eichinvarianz) zu betrachten, künstlich und überflüssig ist.
Dennoch erwies eben diese Idee sich als Schlüssel zur Formulierung der sog. Quantenelektrodynamik (QED).
Und nicht nur das: Sie wies auch den Weg zur verallgemeinerten Quantenfeldtheorie der elektroschwachen Theorie und schließlich der heutigen Standardtheorie zur Beschreibung der starken, der schwachen und der elektromagnetischen Wechselwirkung — der Grand Unified Theory (GUT).
Während in der QED das Eichfeld für ein Photon steht, beschreiben die Eichfelder der allgemeineren Standardtheorie auch die Austauschteilchen der starken und schwachen Wechselwirkung. Hier also sind die Eichfelder keine Hilfsfelder mehr wie in der klassischen Elektrodynamik, sondern die Bosonen selbst.
Wir sehen:
die letztlich zur gelungenen Vereinheitlichung von nun schon 3 der insgesamt 4 physikalischen Grundkräfte geführt hat.
Selbst in der Allgemeinen Relativitätstheorie — für die es bisher ja noch keine Quantenversion gibt — findet sich das Eichprinzip verwirklicht: Das Eichfeld ist dort die Metrik, und die Eichtransformationen sich die allgemeinen Koordinatentransformationen. [Hohnerkamp, 2015]
Nach Wolfgang Osterhage (Seite 154) besteht die Eininvarianz darin, dass man den Potential-Nullpunkt frei wählen (ihn "eichen") kann, ohne dass das Einfluss auf physikalische Vorgänge hat.
Er sagt auch, dass die Erhaltungssätze für Leptonen- und Baryonenzahl mit Quantensymmetrien verknüpft seien und es über die bisher hier genannten Symmetrien für Zeit und Raum nur noch eine weitere geben könne: die Supersymmetrie. Sie beeinflusst den Spinwert — erhöht oder erniedrigt ihn um 1/2 —, macht also aus Fermionen Bosonen und aus Bosonen Fermionen.
Über die vier oben schon erwähnten Erhaltungssätze hinaus — die für Energie, Impuls, Drehimpils und Ladungsdichte — gibt es noch zwei weitere:
- den für die Baryonenzahl ( garantiert durch die SU(2) Symmetrie des starken Isospins ) und
- den für die Leptonenzahl ( garantiert durch die SU(2) Symmetrie des schachen Isospins ).
Neben den fließenden, also kontinuierlichen Symmetrien gibt es weitere, die diskret sind. Es sind dies
- Ladungskonjugation (C, charge),
- Parität (P, räumliche Spiegelung) und
- Zeitumkehr (T, time).
Auch jede Kombination von ihnen erhält — fast immer — das Verhalten des betrachteten Systems. Seltsamerweise aber gibt es da Ausnahmen: Bestimmte Prozesse, in denen die s c h w a c h e Wechselwirkung eine Rolle spielt, verletzen C, P oder CP.
Beitrag 0-222
Gravitative Eichtheorien — können sie ART und Quantentheorie vereinen?
Die Einstein-Cartan-Theorie
Nach Fertigstellung seiner Allgemeinen Relativitätstheore hat Einstein bis hin zu seinem Tode versucht, sie zu einer sog. Einheitlichen Feldtheorie zu verallgemeinern: zu einer Theorie, in der neben der Gravitationskraft auch die eltromagnetische Kraft mit berücksichtigt sein sollte (die Kernkräfte waren zunächst noch gar nicht bekannt).
Schon 1925 dachte er, eine Lösung zu haben, die er dann aber doch bald wieder verwarf.
Einen Ansatz, den er 1928-1931 zusammen mit dem Franzosen Elie Cartan entwickelt hatte — Fernparallelismus mit Torson — betrachtet man heute erneut:
Es liegt ihm die Idee zugrunde, dass Spin Torsion erzeugt und somit zu einer gewissen Verdrillung der Raumzeit führen könnte.
Für Theoretiker hat die Einstein-Cartan-Theorie einige Vorzüge: Sie könnte einen besseren klassischen Grenzfall einer künftigen Quantengravitationstheorie liefern als die ART, welche die Torsion ignoriert.
Und schon in den 70-er Jahren wurde erkannt, dass die sog. Einfache Supergravitationstheorie äquivalent ist zur Einstein-Cartan-Theorie im Falle eines masselosen Feldes mit Spin.
Die Supergravitationstheorie gilt als vielversprechende Etappe auf dem Weg zu einer Weltformel, da sie grundlegende Symmetrien zwischen Kräften und Materie enthält und ein Grenzfall der M-Theorie ist (ebenso wie die 5 Stringtheorien).
Die Einstein-Cartan-Theorie ( EC-Theorie ) — für spinlose Materie identisch mit der ART — ist Spezialfall einer noch umfassenderen Klasse von Gravitationstheorien, den sog.
Gravitative Eichtheorien auf Basis der Lorentz-Poincaré-Gruppe
Obgleich sie mathematisch schon hervorragend ausgearbeitet sind, wissen selbst viele Physiker nichts von ihnen. Das ist erstaunlich, denn sie schlagen eine Brücke hin zur Elementarteilchenphysik, also zur Quantenphysik (die mit Einsteins Theorie zu vereinen, ja erklärtes Ziel aller Quantengravitationstheorien ist).
Die nach Poincaré benannte Symmetriegruppe — sie umfasst die Lorentz-Gruppe — hat 10 Parameter:
Sie alle beschreiben den Übergang von einem Bezugssystem zu einem anderen, welches sich relativ zum ersten mit konstanter Geschwindigkeit bewegt.
Diese Symmetriegruppe repräsentiert sämtliche innerhalb der relativistischen Mechanik möglichen Transformationen. Außerdem lassen sich mit ihr im Rahmen der SRT sämtliche Elementarteilchen klassifizieren hinsichtlich Mass und Spin. Entscheidend hierbei ist, dass Ruhemasse, Spin und Ladung nicht der quantenmechanischen Unbestimmtheitsrelation unterliegen: Sie lassen sich gleichzeitig sehr genau messen und gelten daher als eindeutig bestimmte Eigenschaften der Elementarteilchen.
Mittels der Poincaré-Gruppe — so zeigte sich in den 60-er Jahren — lässt sich auch eine Gravitationstheorie formulieren: die Poincaré-Eichtheorie.
Tatsächlich ist es möglich, noch allgemeinere Geometrien und Symmetrien zu wählen. Sie führen zur Klasse der metrisch-affinen Eichtheorien (mit etwa 100 freien Größen). Die Poincaré-Eichtheorie ist ein Spezialfall der Weyl-Cartan-Eichtheorien (die auch Stauchung berücksichtigen), und die wiederum sind Spezialfall der metrisch-affinen-Eichtheorien (die zudem noch Scherung berücksichtigen).
Quelle:
Rüdiger Vaas: Jenseits von Einsteins Universum (2016),
S. 466-479.
Nach Fertigstellung seiner Allgemeinen Relativitätstheore hat Einstein bis hin zu seinem Tode versucht, sie zu einer sog. Einheitlichen Feldtheorie zu verallgemeinern: zu einer Theorie, in der neben der Gravitationskraft auch die eltromagnetische Kraft mit berücksichtigt sein sollte (die Kernkräfte waren zunächst noch gar nicht bekannt).
Schon 1925 dachte er, eine Lösung zu haben, die er dann aber doch bald wieder verwarf.
Einen Ansatz, den er 1928-1931 zusammen mit dem Franzosen Elie Cartan entwickelt hatte — Fernparallelismus mit Torson — betrachtet man heute erneut:
Es liegt ihm die Idee zugrunde, dass Spin Torsion erzeugt und somit zu einer gewissen Verdrillung der Raumzeit führen könnte.
-
Dennis Sciama — Steven Hawkings Doktorvater — betont, dass man diese Idee nicht einfach nur als ad-hoc-Modifikation der ART zu sehen hat,
sondern dass sie auf einer tiefen gruppentheoretisch und geometrisch begründbaren Grundlage ruht. Er sagt (Zitat):
Wenn der Elektronenspin 1915 schon entdeckt gewesen wäre, dann habe ich wenig Zweifel, dass Einstein es für wünschenswert gehalten hätte, die Torsion in seine ursprüngliche Formulierung der ART mit einzubeziehen. Allerdings sind die normalerweise auftretenden Abweichungen zahlenmäßig s e h r klein, so dass der Vorteil zunächst nur ein gänzlich theoretischer wäre:
Zur ART abweichende Aussagen werden erst für Materiedichten ab etwa 1054 Gramm pro Kubikzentimeter erwartet bei Abständen unter 10-26 cm.
Zum Vergleich: Selbst Neutronensterne haben eine Dichte von » nur « 1016 Gramm pro Kubikzentimeter.
Für Theoretiker hat die Einstein-Cartan-Theorie einige Vorzüge: Sie könnte einen besseren klassischen Grenzfall einer künftigen Quantengravitationstheorie liefern als die ART, welche die Torsion ignoriert.
Und schon in den 70-er Jahren wurde erkannt, dass die sog. Einfache Supergravitationstheorie äquivalent ist zur Einstein-Cartan-Theorie im Falle eines masselosen Feldes mit Spin.
Die Supergravitationstheorie gilt als vielversprechende Etappe auf dem Weg zu einer Weltformel, da sie grundlegende Symmetrien zwischen Kräften und Materie enthält und ein Grenzfall der M-Theorie ist (ebenso wie die 5 Stringtheorien).
- Im Februar 1930 schrieb Einstein an Cartan: ... komme mir mit dieser Theorie vor wie ein Affe, der nach langem Suchen eine ungeheuere Kokosnuss gefunden hat,
sie aber nicht öffnen kann, so dass er nicht einmal weiß, ob etwas drin ist.
Cartan muss es ähnlich gesehen haben, denn er antwortete schon wenige Tage später, man stehe ratlos vor einer Mauer, es sei unklar, wie ein Loch hineingeschlagen werden könnte, und er hoffe auf ein göttliches Wunder.
Solcher und noch anderer Schwierigkeiten wegen, hat Einstein diesen Ansatz dann nicht weiter verfolgt.
Wer denkt, Einstein hätte danach nichts mehr geleistet, irrt sich: Trotz der vielen Sackgassen, in die er geriet, hat er noch bis 1 Tag vor seinem Tod Rechnungungen durchgeführt, von denen er hoffte, dass sie ihn zur angestrebten einheitlichen Feldtheorie führen ...
Sein Nachlass — etwa 63.000 Dokumente und Notizen — wird Forscher noch lange beschäftigen.
Die Einstein-Cartan-Theorie ( EC-Theorie ) — für spinlose Materie identisch mit der ART — ist Spezialfall einer noch umfassenderen Klasse von Gravitationstheorien, den sog.
Obgleich sie mathematisch schon hervorragend ausgearbeitet sind, wissen selbst viele Physiker nichts von ihnen. Das ist erstaunlich, denn sie schlagen eine Brücke hin zur Elementarteilchenphysik, also zur Quantenphysik (die mit Einsteins Theorie zu vereinen, ja erklärtes Ziel aller Quantengravitationstheorien ist).
Die nach Poincaré benannte Symmetriegruppe — sie umfasst die Lorentz-Gruppe — hat 10 Parameter:
- vier für Verschiebungen (Translationen raumzeitlicher Art)
- drei für Drehungen (räumliche Rotation)
- drei für die Loretz-Transformationen (raumzeitliche Rotationen)
Sie alle beschreiben den Übergang von einem Bezugssystem zu einem anderen, welches sich relativ zum ersten mit konstanter Geschwindigkeit bewegt.
Diese Symmetriegruppe repräsentiert sämtliche innerhalb der relativistischen Mechanik möglichen Transformationen. Außerdem lassen sich mit ihr im Rahmen der SRT sämtliche Elementarteilchen klassifizieren hinsichtlich Mass und Spin. Entscheidend hierbei ist, dass Ruhemasse, Spin und Ladung nicht der quantenmechanischen Unbestimmtheitsrelation unterliegen: Sie lassen sich gleichzeitig sehr genau messen und gelten daher als eindeutig bestimmte Eigenschaften der Elementarteilchen.
Mittels der Poincaré-Gruppe — so zeigte sich in den 60-er Jahren — lässt sich auch eine Gravitationstheorie formulieren: die Poincaré-Eichtheorie.
Tatsächlich ist es möglich, noch allgemeinere Geometrien und Symmetrien zu wählen. Sie führen zur Klasse der metrisch-affinen Eichtheorien (mit etwa 100 freien Größen). Die Poincaré-Eichtheorie ist ein Spezialfall der Weyl-Cartan-Eichtheorien (die auch Stauchung berücksichtigen), und die wiederum sind Spezialfall der metrisch-affinen-Eichtheorien (die zudem noch Scherung berücksichtigen).
Beitrag 0-500
Einstein Feldgleichung wenigstens grob verstehen
Einsteins Feldgleichung
erklärt und kommentiert durch Helmut Satz
Quelle: Helmut Satz: Kosmische Dämmerung (2016), S. 181-184
erklärt und kommentiert durch Helmut Satz
Helmut Satz (2016):
Die ursprünglich von Einstein aufgestellten Gleichungen lauteten
Rμν – (1/2) R gμν = c-4 8πG Tμν ,
wobei G die Newtonsche Gravitationskonstante und c die Lichtgeschwindigkeit bezeichnet.
Die Indizes μ und ν geben Zeit und Raum an und durchlaufen somit die Werte 0 (Zeit) und 1,2,3 (Raum).
Der sog. metrische Tensor gμν definiert die Raumzeit ohne Gravitation, d.h. den flachen Minkowski-Raum. R ist ein Skalenfaktor (sog. Ricci-Krümmungsskalar).
Der sog. Energie-Impuls-Tensor Tμν beschreibt den Rauminhalt. d.h. die Energiedichte ρ im Raum sowie den daraus resultierenden Druck p.
Der sog. (Ricci-) Krümmungs-Tensor Rμν schließlich beschreibt die durch den Rauminhalt erzeugte Krümmung von Raum und Zeit.
Alle Tensoren der Gleichung sind symmetrisch (so dass man statt 16 nur 10 Gleichungen hat).
Eine Aussage dieser Gleichungen ist, dass sich die Größe des Weltraums aufgrund seines Inhalts verändern kann.
Das Maß dieser Änderung ist der schon erwähnte Skalenfaktor R = a(t) — er skaliert die Abstände im Raum und somit die Raumgröße.
Für ihn ergeben sich aus Einsteins Gleichung zwei Beziehungen, die als erster 1922 der russische Physiker Alexander Friedmann hergeleitet hat. Die erste
H2 = (( da/dt )/a )2 = ( 8πG/3 )ρ – k/a2 ,
bestimmt die Geschwindigkeit v = da/dt, mit der sich die Skala verändert ( H ist somit das, was man heute den sog. Hubble-Parameter nennt).
ρ ist die Energiedichte im Raum, und
k spezifiziert die Raumstruktur: Für flachen Raum ist k = 0, für sphärischen k = 1 unf für hyperbolischen k = –1.
Friedmanns zweite Gleichung bestimmt die Veränderung der Skalengeschwindigkeit (da/dt)dt = a'' = v' und sagt:
a''/a = –( 4/3 )πG ( ρ + 3p ) ,
Dieser zweite von Friedmann abgeleitete Zusammenhang zeigt, dass Einsteins Wunsch nach einem statischen Universum durch seine Gleichungen in ihrer Urform (s.o.) nicht erfüllbar ist, denn selbst wenn man bei sphärischer Krümmung des Raumes (k = 1) Friedmanns zweite Gleichung zu irgend einem Zeitpunkt da/dt = 0 zulassen würde, zeigt die Gleichung, dass sich das rasch wieder ändern muss.
Einstein sah nun aber, dass die mathematische Struktur seiner Gleichungen eine Abänderung erlaubt: Man kann der linken Seite einen additiven Term hinzufügen, so dass die Gleichung dann lautet:
Rμν – (1/2) R gμν + Λμν = c-4 8πG Tμν ,
wo Λ eine universelle, positive, räumlich und zeitlich konstante Größe ist (eine sog. kosmologische Konstante).
Sie hat zur Folge, dass sich zur rechten Seite beider Gleichungen von Friedmann die Zahl Λ/3 addiert.
Damit schien Einsteins Wunsch nach einem statischen Universum zunächst erfüllbar: Bei sphärischer Raumkrümmung nämlich (k = 1) gibt es gemeinsame Werte Λ, p und ρ, welche die erste und die zweite Ableitung von a nach der Zeit zu Null machen.
Schon bald aber wurde klar, dass jede noch so kleine zeitliche Schwankung der Energiedichte das statische Universum instabil machen würde in dem Sinne, dass der Raum dann sofort zu expandieren oder zu kontrahieren beginnen würde.
Hinzu kam Hubbles Entdeckung, des expandierenden Weltalls: Das Universum ist tatsächlich nicht statisch.
Einstein soll deswegen die Einführung seiner "kosmologischen" Konstanten als "größte Eselei seines Lebens" bezeichnet haben.
Heute denkt man eher, dass seine Konstante vielleicht doch Sinn macht:
Mit Λ = 0 nämlich kann man zwar ein expandierendes Universum erhalten, aber nur eines, bei der die Expansionsrate mit der Zeit abnimmt.
Mitte der 1990-er Jahre gesammelte Supernova-Daten zeigen nun aber, dass die Expansionsrate sich mit der Zeit vergrößert statt verkleinert, was ein positives, hinreichend großes Λ erfordert.
Erst damit lassen sich die neueren Vorstellungen von Multiversum und Iflation problemlos in den gegebenen Rahmen einfügen.
Man schreibt den Λ-Term dann auf die rechte Seite der Gleichung, um zu betonen, dass die Entwicklung der Krümmung des Raumes
- nicht nur durch die von den Objekten im Raum kommende Energiedichte T bestimmt ist,
- sondern eben auch durch ein dem Raum selbst innewohnendes, konstantes Feld Λ der Gravitation entgegen wirkender Energie.
Mit Hilfe der genannten Supernova-Beobachtungsdaten kann man die Größe von Λ dann sogar errechnen.
Und so gibt man Einsteins Feldgleichung heute die Form
Rμν – (1/2) R gμν = c-4 8πG Tμν – Λμν ,
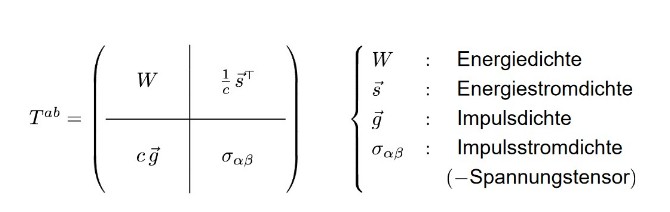
Der Energie-Impuls-Tensor
tags: Theorie1gegreit Teilchen1gegreit Einstein1gegreit
 Nach oben
Nach oben