Beitrag 0-469
Unter welchen Umständen SRT schon ART ist
Unter welchen Bedingungen ein gegebenes Raumzeit-Szenario S
sich per SRT ebenso genau wie per ART durchrechnen lässt
Das sog. Zwillingsparadoxon ist Spezialfall eines Szenarios S, in dem sich zwei Objekte C und D auf unterschiedlichen Weltlinien durch die Raumzeit bewegen.
Die notwendige und hinreichende Bedingung dafür, dass S selbst schon mit Mitteln der SRT — quantitativ wie qualitativ — beliebig genau behandelbar ist, besteht darin, dass S per SRT modellierbar ist.
Dies lässt sich einsehen wie folgt:
Im Sinne der ART ist die Raumzeit eine differenzierbare Mannigfaltigkeit, d.h. wer darin räumlich weit verteilte Szenarien behandeln will, kann sie nur behandeln mit Hilfe von Störungsrechnung und Argumentation in den Tangentenräumen, d.h. anhand sog. » Karten «, deren jede eine offene Umgebung des Ereignisses E(T) zeigt, in dem der Tangentenraum T — ein 4-dimensionaler Vektorraum mit Minkowsi-Metrik — die Raumzeit der ART berührt.
Brauchbar ist jede dieser Karten aber nur bis hin zum Beobachtungshorizont H(E) des Ereignisses E = E(T) = Ursprung des in T genutzten Koordinatensystems.
Aber auch in der Raumzeit gibt es entsprechend große und kleine Regionen, und so komme ich zur Einsicht:
Das Szenario S ist mit Hilfe der SRT genau dann — und in diesem Fall sogar beliebig genau — durchrechenbar, wenn
Dieses Ergebnis bleibt richtig auch für den Fall, dass zwischen den Weltlinien von C einerseits und D andererseits ein oder mehrere Schwarze Löcher liegen (für deren Inneres Karten, welche beide Weltlinien ganz oder teilweise zeigen, natürlich nichts aussagen würden: Jene Karten wären dort einfach nicht definiert).
sich per SRT ebenso genau wie per ART durchrechnen lässt
Das sog. Zwillingsparadoxon ist Spezialfall eines Szenarios S, in dem sich zwei Objekte C und D auf unterschiedlichen Weltlinien durch die Raumzeit bewegen.
Die notwendige und hinreichende Bedingung dafür, dass S selbst schon mit Mitteln der SRT — quantitativ wie qualitativ — beliebig genau behandelbar ist, besteht darin, dass S per SRT modellierbar ist.
Dies lässt sich einsehen wie folgt:
Im Sinne der ART ist die Raumzeit eine differenzierbare Mannigfaltigkeit, d.h. wer darin räumlich weit verteilte Szenarien behandeln will, kann sie nur behandeln mit Hilfe von Störungsrechnung und Argumentation in den Tangentenräumen, d.h. anhand sog. » Karten «, deren jede eine offene Umgebung des Ereignisses E(T) zeigt, in dem der Tangentenraum T — ein 4-dimensionaler Vektorraum mit Minkowsi-Metrik — die Raumzeit der ART berührt.
Brauchbar ist jede dieser Karten aber nur bis hin zum Beobachtungshorizont H(E) des Ereignisses E = E(T) = Ursprung des in T genutzten Koordinatensystems.
Man kann sich das gut vorstellen, indem man sich ein Wasserfahrzeug W vorstellt, mit dessen Hilfe eine Persion P über den Atlantik von z.B. Amsterdam nach z.B. New York reist:
Über weite Strecken der Reise hinweg wird — der Krümmung der Erdoberfläche wegen — keine Küste sichtbar sein, gegen Ende der Reise aber wird sich das ändern: Der Beobachtungshorizont H(P) von P verschiebt sich mit W, so dass die Karten, die man an Bord von W nutzt — sie entsprechen den eben erwähnten "Karten" im Sinne der Differentialgeometrie — ständig ausgetauscht werden müssen.
Nun gibt es aber auch kleine Gewässer, wie etwa den Chiemsee, den zu überqueren man die zu Beginn der Reise gewählte Karte nie auszutauschen braucht, da jeder Weg, den das Schiff W dort nehmen kann, deutlich kürzer ist als der Radius des Beobachtungshorizonts der Ablegestelle.
Aber auch in der Raumzeit gibt es entsprechend große und kleine Regionen, und so komme ich zur Einsicht:
Das Szenario S ist mit Hilfe der SRT genau dann — und in diesem Fall sogar beliebig genau — durchrechenbar, wenn
- eine Raumzeit-Karte K existiert, welche komplett die beiden Weltlinien von C und D zeigt
- und wenn ferner die Weltlinien von C und D durch kein nennenswertes Gravitationsfeld führen.
Dieses Ergebnis bleibt richtig auch für den Fall, dass zwischen den Weltlinien von C einerseits und D andererseits ein oder mehrere Schwarze Löcher liegen (für deren Inneres Karten, welche beide Weltlinien ganz oder teilweise zeigen, natürlich nichts aussagen würden: Jene Karten wären dort einfach nicht definiert).
Beitrag 0-342
C... Kiefer erklärt das Zwillingsparadoxon richtig — Joachim Schulz aber denkt zu kurz
Claus Kiefer erklärt das Zwillingsparadoxon richtig
— Joachim Schulz aber, der ihm widerspricht, denkt nicht weit genug —
Quelle: Claus Kiefer: Der Quantenkosmos, Fischer 2008, S. 36-37
Claus Kiefer studierte Physik und Astronomie. Er promovierte 1988 über den Begriff der inneren Zeit in der kanonischen Quantentheorie der Gravitation. Nach seiner Habilitation lehrte er an den Universitäten in Zürich und Freiburg. Seit 2001 ist der Professor für Theoretische Physik an der Universität Köln.
Joachim Schulz ist promovierter Physiker, aber kein Experte für Relativitätstheorie.
Bei seiner Argumentation in [JS] übersieht Schulz, dass nur unterschiedliche Beschleunigung der Zwillinge ihre Weltlinien unterschiedlich lang machen kann. Dies ergibt sich allein schon aus Symmetriegründen.
Dennoch kommt — wie Schulz ganz richtig zeigt — der Altersunterschied auch in Phasen zustande, in denen keine Beschleunigung vorliegt. Er kommt also zustande
Reisegeschwindigkeit sowie Lage und Krümmung der Weltlinie des reisenden Zwillings werden durch seine Beschleunigung bestimmt.
Damit gilt gleiches für seinen Verbrauch an Eigenzeit während der Reise, denn der entspricht der Länge der Weltlinie.
Hier nun, wie sich das einsehen lässt:
Ganz analog zur Argumentation von Joachim Schulz ist jene von Martin Bäker im Abschnitt » The Good « seines Blog Posts Erklärungen zum Zwillingsparadoxon, wo Bäker argumentiert wie folgt:
Statt, wie Bäker, auf den Bonus hinzuweisen, argumentiere ich wie folgt:
Konsequenz daraus: Das uns durch das Bild 1 nahegelegte Rechenmodell ist — während der gesamten Umkehrphase — allzu unrealistisch — so dass man seinem Ergebnis nicht trauen kann.
Gleiches gilt für das dazu analoge Rechenmodell von Joachim Schulz, welches ja ebenfalls sämtliche beschleunigten Phasen der Reise als unteilbare Augenblicke annimmt.
In vollem Umfang richtig — auch hinsichtlich der mindestens am Umkehrpunkt notwendigen Beschleunigungsphase — wird die Situation nun aber dargestellt im Diagramm hier (man beachte die dünnen roten Linien, welche in Bäkers Diagramm den dort blau und rot gezeigten entsprechen):

Erst dieses Bild und das nächste machen klar, dass
sich das Zwillingsparadoxon allein schon mit Hilfe der SRT in überzeugender Weise lösen lässt
und in welcher Weise der Dopplereffekt sich bemerkbar macht:
Für den entstehenden Altersunterschied der Zwillinge spielt er keine Rolle,
wohl aber für die Ankunftszeiten zwischen A und B ausgetauschter Nachrichten.
Wie man sieht, ist der Weg, den B durch den Raum nimmt, gekrümmt.
Diese Krümmung verlängert in der Formel für die Minkowski-Metrik den raumartigen Anteil der raumzeitlichen Distanz und
verkürzt
deswegen entsprechend ihren zeitartigen Anteil,
d.h. die Eigenzeit von B im Vergleich zur Eigenzeit von A zwischen Antritt und Ende der Reise.
Wie man ferner sieht, bleibt in nichtbeschleunigten Phasen der Reise der Prozentsatz, zu dem die Eigenzeit von B der Eigenzeit von A gegenüber gedehnt ist, konstant.
Andere Dehnung der Eigenzeit von B ergibt sich (vorzeichenrichtig) erst wieder, wenn B beschleunigt (bzw. abbremst).
In diesem Diagramm wird das nur deswegen nicht deutlich, da es beschleunigte Phasen ja gar nicht zeigt (bzw. auflöst).
Solche einfachen Diagramme zeigen also nicht jede Sicht der Zwillinge, sondern einfach nur ihre jeweilge Sicht aus den 3 Perspektiven heraus, welche den Phasen unbeschleunigter Bewegung entsprechen.
Im folgenden Bild sind diese drei Sichten auf ein und dieselbe Raumzeit farblich unterschieden dargestellt:
Die punktierte Linie darin ist die durch die Raumzeit führende Weltlinie des Lichts.
Die geraden unterbrochenen Linien (jeweils parallel zur Raumachse einer Sicht) stellen dar, was aus jeder einzelnen dieser 3 Sichten heraus gleichzeitig geschieht.
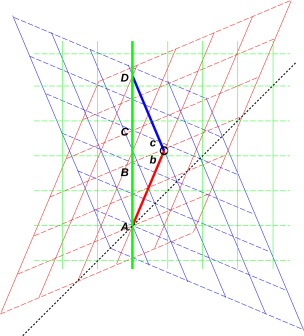
Quelle: John Denker (2003)
Bild 4 zeigt sehr deutlich, dass Beschleunigung nicht die Struktur der Raumzeit verändert, sondern lediglich die Sicht des Beschleunigten auf die Raumzeit: Das Koordinatensystem, aus dem heraus er die Welt betrachtet, dreht sich während seiner Beschleunigung mehr und mehr, so dass seine Raumachse neue Richtung bekommt). Bild 2 zeigt, dass dies bei wachsender Beschleunigung eine Drehung gegen den Uhrzeigersinn, bei fallender Beschleunigung aber eine im Uhrzeigersinn ist (wenn Serenas Reiseziel sich rechts im Bild findet).
Bild 2 zeigt auch, dass Beschleunigung den Weg durch die Raumzeit krümmt und somit kürzer macht.
Nur dieser Krümmung wegen, die es ohne Beschleunigung nicht gegeben hätte, ergibt sich für die Zwillinge ein nicht mehr rückgängig zu machender Altersunterschied.
Joachim Schulz irrt demnach gründlich, wenn er behauptet nicht Beschleunigung mache die Zeit (sprich: den Altersunterschied).
Richtig ist stattdessen:
Beschleunigung bestimmt Eigenzeit, Geschwindigkeit bestimmt das Messergebnis (sprich: die Zeit als beobachteten Fluss der Zeit).
Was wir Zeit nennen, ist gemessene Zeit,
d.h. durch stetige Abstandsänderung und die Endlichkeit der Lichtgeschwindigkeit relativ gewordenes Ergebnis
einer Beobachtung des Flusses der Eigenzeit des beobachteten Objekts.
Fußnote:
Nachdem ich versucht habe, zentrale Aussagen diese Seite im Rahmen der Kommentare #470-#718 zu Martin Bäkers Blogpost qualitätsgesichert zu bekommen, wurde mir gegen Ende der Diskussion dort klar, dass — Missverständnisse zu vermeiden — klar sein sollte, wie ich und meine Diskussionspartner dort die 4 Diagramme oben lesen. Wir lesen sie wie folgt:
Grenzwertbetrachtung
Zur Kenntnis nehmen sollte man, dass Bild 2 in Kombination mit der Erkenntnis, dass der schließlich für die Zwillinge entstehende Altersunterschied prozentual umso deutlicher ausfallen wird, je höher die Beschleunigung ist, mit der B die Reise durchführt, auch noch zeigt:
Extrem hohe Beschleunigung gleich von Anfang an — ebenso wie zu Beginn der Rückreise — führt schnell zu hoher Geschwindigkeit und damit zu schnellerem Erreichen des Ziels, so dass A weniger lange auf die Rückkehr von B zu warten hat.
Die Bilder 1 und 2 werden dadurch niedriger (bei gleicher Breite) und der Winkel zwischen den Raumachsen der beiden Zwillinge könnte so gut auf bis fast 90 Grad wachsen (immer vorausgesetzt, B hält so hohe Beschleunigung aus, was aber gut sein könnte, wenn B keine Person, sondern nur eine Uhr ist). Je entschiedener also beschleunigt wird, desto mehr führt die Weltlinie von B dann fast nur noch durch den Raum, also fast gar nicht mehr durch die Zeit.
Ihre am Umkehrpunkt dann zunehmend stärker werdende Krümmung korresponiert mit dem gegen Null strebenden Verhältnis Eigenzeit(B)/Eigenzeit(A).
Grenzübergang zeigt:
Was sich mit Lichtgeschwindigkeit durch den Raum bewegt
— Licht etwa oder Gravitationswellen —
altert gar nicht.
— Joachim Schulz aber, der ihm widerspricht, denkt nicht weit genug —
Claus Kiefer (wörtlich zitiert):
[ Im Szenario des Zwillingsparadoxons ] verlässt ein Zwilling die Erde mit einem Raumschiff, während sein Bruder auf der Erde verbleibt. Der Raumfahrer rast mit hoher Geschwindigkeit ins All, kehrt um und rast wieder zur Erde zurück. Bei seiner Rückkehr stellt er fest, dass sein Bruder im Vergleich zu ihm gealtert ist. Wie lässt sich das verstehen?
Da wegen der Zeitdilatation alle Uhren (und somit auch alle physiologischen Vorgänge im Raumschiff) in bezug auf den irdischen Zwilling verlangsamt sind, ist ja zu erwarten, dass der Raumfahrer zum Zeitpunkt seiner Rückkehr weniger gealtert ist.
Doch gilt dies nicht auch umgekehrt? Ist nicht der irdische Zwilling in bezug auf seinen Bruder im Raumschiff bewegt und sollte deshalb weniger altern?
Der Pferdefuß bei dieser Gedankenkette liegt darin, dass der Raumfahrer Beschleunigung erfährt, der irdische hingegen nicht (jedenfalls in guter Näherung). Um nämlich umkehren zu können, muss der reisende Zwilling seine Geschwindigkeit ändern. Das Relativitätsprinzip gilt jedoch nur für Initialsysteme, nicht für beschleunigte Systeme. Von daher ist die Symmetrie zwischen beiden Zwillingen gebrochen.
In Minkowskis Raumzeitformulierung lässt sich leicht erkennen, dass der irdische Zwilling bei Rückkehr älter ist:
Die verflossene Zeit, die der jeweilige Zwilling auf seiner Uhr abliest — man spricht hier von sog. Eigenzeit —, lässt sich direkt aus der Länge der jeweiligen Weltlinien im Minkowski-Raum ablesen.
Umgekehrt zur rein räumlichen Geometrie gilt aber, dass die längste Zeit für einen Beobachter auf einer geraden Weltlinie vergeht. Jede Krümmung verkürzt die Eigenzeit. Da die Weltlinie des reisenden Zwillings gekrümmt ist, entspricht ihr im Vergleich zur Weltline des irdischen Zwillings eine kleinere Eigenzeit.
Claus Kiefer studierte Physik und Astronomie. Er promovierte 1988 über den Begriff der inneren Zeit in der kanonischen Quantentheorie der Gravitation. Nach seiner Habilitation lehrte er an den Universitäten in Zürich und Freiburg. Seit 2001 ist der Professor für Theoretische Physik an der Universität Köln.
Joachim Schulz ist promovierter Physiker, aber kein Experte für Relativitätstheorie.
Bei seiner Argumentation in [JS] übersieht Schulz, dass nur unterschiedliche Beschleunigung der Zwillinge ihre Weltlinien unterschiedlich lang machen kann. Dies ergibt sich allein schon aus Symmetriegründen.
Dennoch kommt — wie Schulz ganz richtig zeigt — der Altersunterschied auch in Phasen zustande, in denen keine Beschleunigung vorliegt. Er kommt also zustande
- ganz wesentlich unterschiedlicher Beschleunigung wegen,
- aber dennoch nicht nur während der beschleunigten Phasen der Reise.
Damit gilt gleiches für seinen Verbrauch an Eigenzeit während der Reise, denn der entspricht der Länge der Weltlinie.
Hier nun, wie sich das einsehen lässt:
Ganz analog zur Argumentation von Joachim Schulz ist jene von Martin Bäker im Abschnitt » The Good « seines Blog Posts Erklärungen zum Zwillingsparadoxon, wo Bäker argumentiert wie folgt:
Martin Bäker (analog zu Schulz):
Entscheidend ist anscheinend nicht die Beschleunigung, sondern etwas anderes. Das wird beispielsweise in dieser Grafik deutlich:
Betrachtet werden ein stationärer Zwilling (Teresa = A) und ein reisender (Serena = B):
Das Bild zeigt den Weg von Serena (B) bis in 3 Lichtjahre Entfernung mit einer Geschwindigkeit von 60% der Lichtgeschwindigkeit und anschließender Rückkehr eingetragen in einem Raumzeit-Diagramm. Auf der horizontalen Achse ist der Ort (gemessen von A aus) aufgetragen, auf der vertikalen Achse die Zeit, die für A vergeht. Die Punkte liegen (auf der jeweiligen Achse) im Abstand von einem Jahr. Die roten und blauen Linien zeigen, welche Ereignisse für B jeweils zur selben Zeit stattfinden.
Wenn B (Serena) von A wegfliegt, dann sieht sie A (Teresa) verlangsamt, die rote Linie, die bei Serenas zweitem Punkt (also nach zwei Jahren) liegt, trifft die senkrechte Achse, die Teresa beschreibt, an einem Punkt, wo für Teresa weniger als zwei Jahre vergangen sind.
Umgekehrt zeigt eine horizontale Linie, die ihr euch bei Teresa zur Zeit nach zwei Jahren denkt, dass hier für Serena weniger als 2 Jahre vergangen sind, die Situation ist also symmetrisch. Auf dem Rückflug ist es ähnlich, auch hier könnt ihr euch leicht überzeugen, dass jede die anderen verzögert sieht (am einfachsten fangt ihr dazu oben an und guckt sozusagen in die Vergangenheit, dann ist das Bild ja genau symmetrisch).
Entscheidend aber ist — und das macht dieses Diagramm sehr schön deutlich —, dass es einen weiten Bereich von Ereignissen bei Teresa (A) gibt, die für den reisenden Zwilling (Serena = B) mit gar nichts gleichzeitig sind. Und das hat nichts mit irgendwelchen Beschleunigungen zu tun, sondern nur damit, dass Serena ihr Bezugssystem wechselt.
Das Zwillingsparadoxon kommt demnach durch einen Wechsel des Bezugssystems zustande (rein rechnerisch wenigstens).
So ein Wechsel des Bezugssystems kann in der Physik oft zu scheinbaren Unstimmigkeiten in der Beschreibung führen, ein Beispiel dafür habe ich vor einiger Zeit hier erklärt mit Auflösung des Rätsels hier.
Wikipedia zeigt übrigens auch noch eine Grafik, die den Fall einer kontinuierlichen Beschleunigung veranschaulicht — auch da sieht man nochmal, dass die SRT wirklich und tatsächlich kein Problem hat, mit Beschleunigungen zu hantieren.
Physikalisch ist das sicherlich eine sehr saubere und sinnvolle Erklärung, die kein bisschen in die Irre führt. Allerdings ist dieser Wechsel des Bezugssystems (seine Folgen betreffend) nicht wirklich anschaulich. Man denkt, er könne nur beschreibungstechnische Bedeutung haben. Deswegen nun — sozusagen als Bonus — das Märchen bzw. Paradoxon von Raum und Zeit: ... [man sollte seine Lösung genau durchdenken].
Statt, wie Bäker, auf den Bonus hinzuweisen, argumentiere ich wie folgt:
Nach Bild 1 besteht die Umkehrphase aus nur einem einzigen Ereignis, was so in Wirklichkeit aber nie sein kann. Genauer:
Bild 1 suggeriert uns, es gäbe für Serena nur zwei Bezugssysteme: das der Hinreise und das der Rückreise. Tatsächlich aber wird Serenas Bezugssystem stetig gedreht – als Initialsystem also ständig ausgetauscht – während aller Phasen ihrer Reise, in denen sie sich beschleunigt bewegt.
Die Steigung der dicken roten Linie zeigt die Geschwindigkeit von Serena (relativ zu Teresa).
Konsequenz daraus: Das uns durch das Bild 1 nahegelegte Rechenmodell ist — während der gesamten Umkehrphase — allzu unrealistisch — so dass man seinem Ergebnis nicht trauen kann.
Gleiches gilt für das dazu analoge Rechenmodell von Joachim Schulz, welches ja ebenfalls sämtliche beschleunigten Phasen der Reise als unteilbare Augenblicke annimmt.
In vollem Umfang richtig — auch hinsichtlich der mindestens am Umkehrpunkt notwendigen Beschleunigungsphase — wird die Situation nun aber dargestellt im Diagramm hier (man beachte die dünnen roten Linien, welche in Bäkers Diagramm den dort blau und rot gezeigten entsprechen):

sich das Zwillingsparadoxon allein schon mit Hilfe der SRT in überzeugender Weise lösen lässt
und in welcher Weise der Dopplereffekt sich bemerkbar macht:
Für den entstehenden Altersunterschied der Zwillinge spielt er keine Rolle,
wohl aber für die Ankunftszeiten zwischen A und B ausgetauschter Nachrichten.
Wie man sieht, ist der Weg, den B durch den Raum nimmt, gekrümmt.
Diese Krümmung verlängert in der Formel für die Minkowski-Metrik den raumartigen Anteil der raumzeitlichen Distanz und
verkürzt
deswegen entsprechend ihren zeitartigen Anteil,
d.h. die Eigenzeit von B im Vergleich zur Eigenzeit von A zwischen Antritt und Ende der Reise.
Wie man ferner sieht, bleibt in nichtbeschleunigten Phasen der Reise der Prozentsatz, zu dem die Eigenzeit von B der Eigenzeit von A gegenüber gedehnt ist, konstant.
Andere Dehnung der Eigenzeit von B ergibt sich (vorzeichenrichtig) erst wieder, wenn B beschleunigt (bzw. abbremst).

In diesem Diagramm wird das nur deswegen nicht deutlich, da es beschleunigte Phasen ja gar nicht zeigt (bzw. auflöst).
Solche einfachen Diagramme zeigen also nicht jede Sicht der Zwillinge, sondern einfach nur ihre jeweilge Sicht aus den 3 Perspektiven heraus, welche den Phasen unbeschleunigter Bewegung entsprechen.
Im folgenden Bild sind diese drei Sichten auf ein und dieselbe Raumzeit farblich unterschieden dargestellt:
Die punktierte Linie darin ist die durch die Raumzeit führende Weltlinie des Lichts.
Die geraden unterbrochenen Linien (jeweils parallel zur Raumachse einer Sicht) stellen dar, was aus jeder einzelnen dieser 3 Sichten heraus gleichzeitig geschieht.

Quelle: John Denker (2003)
Bild 4 zeigt sehr deutlich, dass Beschleunigung nicht die Struktur der Raumzeit verändert, sondern lediglich die Sicht des Beschleunigten auf die Raumzeit: Das Koordinatensystem, aus dem heraus er die Welt betrachtet, dreht sich während seiner Beschleunigung mehr und mehr, so dass seine Raumachse neue Richtung bekommt). Bild 2 zeigt, dass dies bei wachsender Beschleunigung eine Drehung gegen den Uhrzeigersinn, bei fallender Beschleunigung aber eine im Uhrzeigersinn ist (wenn Serenas Reiseziel sich rechts im Bild findet).
Bild 2 zeigt auch, dass Beschleunigung den Weg durch die Raumzeit krümmt und somit kürzer macht.
Nur dieser Krümmung wegen, die es ohne Beschleunigung nicht gegeben hätte, ergibt sich für die Zwillinge ein nicht mehr rückgängig zu machender Altersunterschied.
Joachim Schulz irrt demnach gründlich, wenn er behauptet nicht Beschleunigung mache die Zeit (sprich: den Altersunterschied).
Richtig ist stattdessen:
Beschleunigung bestimmt Eigenzeit, Geschwindigkeit bestimmt das Messergebnis (sprich: die Zeit als beobachteten Fluss der Zeit).
Was wir Zeit nennen, ist gemessene Zeit,
d.h. durch stetige Abstandsänderung und die Endlichkeit der Lichtgeschwindigkeit relativ gewordenes Ergebnis
einer Beobachtung des Flusses der Eigenzeit des beobachteten Objekts.
Fußnote:
Nachdem ich versucht habe, zentrale Aussagen diese Seite im Rahmen der Kommentare #470-#718 zu Martin Bäkers Blogpost qualitätsgesichert zu bekommen, wurde mir gegen Ende der Diskussion dort klar, dass — Missverständnisse zu vermeiden — klar sein sollte, wie ich und meine Diskussionspartner dort die 4 Diagramme oben lesen. Wir lesen sie wie folgt:
- Zum 1. Bild: Es besteht Einigkeit darüber, dass es die für Serena notwendigen Beschleunigungsphasen ignoriert — genauer: als Phasen zeitlicher Länge Null betrachtet,
was man als realitätsfern einzustufen hat — und dass ferner gilt:
Die roten und blauen Linien zeigen, welche Ereignisse aus Sicht des reisenden Zwillings (B = Serena) jeweils zur selben Zeit stattfinden.
- Zum 2. Bild: Die waagrechten dünnen blauen Linien zeigen, welche Ereignisse in Teresa Koordinatensystem gleichzeitig sind.
Die dünnen roten Linien zeigen, welche Ereignisse im jeweiligen Koordinatensysten von Serena (dem reisenden Zwilling B) zur Zeit seiner Hinreise, Umkehr und Rückreise gleichzeitig sind.
Die dickeren roten Punkte markieren die Zeitpunkte, zu denen der rote Zwilling die Eigenbeschleunigung ändert.
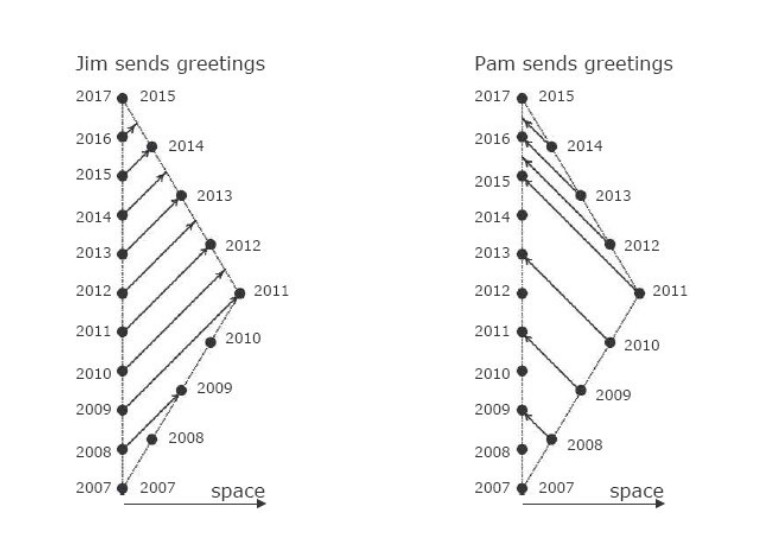
- Zum 3. Bild: Es zeigt, zu welcher Zeit durch A oder B abgesandte Signale (über Funk abgesetzte Greetings) bei der Schwester ankommen.
Deutlich erkennbar im Bild ist der Dopplereffekt.
- Zum 4. Bild: Es zeigt, wie ein und dieselbe Raumzeit sich unter den Koordinatensystemen darstellt, welche genutzt werden
- von Teresa die ganze Zeit über (das grüne),
- von Serena während der unbeschleunigten Phase ihrer Hinreise zum Umkehrpunkt (das rote), bzw.
- von Serena während der unbeschleunigten Phase ihrer Rückreise (das blaue).
Extrem deutlich wird die Relativität der Gleichzeitigkeit: Gleichzeitig zu sein bedeutet, im jeweils genutzten Koordinatensystem denselben ct-Wert zu haben.
Deutlich wird auch, dass die Weltlinie des Lichts — so wie man das von allen Weltlinien erwartet — ein NICHT relativer Begriff ist.
Wo unterschiedliche Ereignisse auf ihr liegen, haben sie raumzeitlichen Abstand ds = 0 (man sagt dann auch, sie hätten lichtartigen Abstand).
Wenn wir einen fernen Stern beobachten, ist das ein Ereignis, welches lichtartigen Abstand hat von dem Ereignis, in dem der Stern — irgendwann in seiner Vergangenheit — das Bild seiner selbst abgestrahlt hat, das wir eben jetzt empfangen. - von Teresa die ganze Zeit über (das grüne),
Zur Kenntnis nehmen sollte man, dass Bild 2 in Kombination mit der Erkenntnis, dass der schließlich für die Zwillinge entstehende Altersunterschied prozentual umso deutlicher ausfallen wird, je höher die Beschleunigung ist, mit der B die Reise durchführt, auch noch zeigt:
Extrem hohe Beschleunigung gleich von Anfang an — ebenso wie zu Beginn der Rückreise — führt schnell zu hoher Geschwindigkeit und damit zu schnellerem Erreichen des Ziels, so dass A weniger lange auf die Rückkehr von B zu warten hat.
Die Bilder 1 und 2 werden dadurch niedriger (bei gleicher Breite) und der Winkel zwischen den Raumachsen der beiden Zwillinge könnte so gut auf bis fast 90 Grad wachsen (immer vorausgesetzt, B hält so hohe Beschleunigung aus, was aber gut sein könnte, wenn B keine Person, sondern nur eine Uhr ist). Je entschiedener also beschleunigt wird, desto mehr führt die Weltlinie von B dann fast nur noch durch den Raum, also fast gar nicht mehr durch die Zeit.
Ihre am Umkehrpunkt dann zunehmend stärker werdende Krümmung korresponiert mit dem gegen Null strebenden Verhältnis Eigenzeit(B)/Eigenzeit(A).
Grenzübergang zeigt:
— Licht etwa oder Gravitationswellen —
altert gar nicht.
Beitrag 1997-135
Die Paradoxie der Zwillinge: Unterschiedlich beschleunige Objekte altern unterschiedlich schnell
z.B. das Experiment von Hafele & Keating ( und ganz besonders sein Ergebnis )
Horst in 1997-129:Grtgrt in 1997-127:
Der logische Fehler, der Bernhardt mit dieser seiner (fett gedruckten) Aussage unterläuft, besteht darin, anzunehmen, dass es möglich wäre, das Zwillingsparadoxon auch in W i r k l i c h k e i t so abzuwandeln, dass es zu keinerlei Beschleunigungskräften mehr kommt. Leider geht das aber gar nicht.
Hallo Grtgrt.
Was verstehst du unter dem Zwillingsparadoxon in W i r k l i c h k e i t ?
Beitrag 1997-111
Wer Spezielle Relativitätstheorie (SRT) verstehen will, muss sich klar gemacht haben ...
Wer die SRT verstehen will, sollte wissen:
An Okotombrok, Eugen, Henry, Horst und Stueps:
Euch scheint nicht bewusst zu sein, dass die SRT — anders als die ART —
Und speziell für Horst, sei gesagt, dass das Wort "sehen" hier nicht allzu wörtlich verstanden werden darf:
Es steht für "sehen könnten unter der Voraussetzung, dass jedes Objekt die Fähigkeit hat, beliebig weit absolut genau zu sehen".
In moderner Terminologie kann man das Szenario, in dem die SRT argumentiert, ohne Beschränkung der Allgemeinheit beschreiben wie folgt:
KONSEQUENZ all dessen ist ( jeder überlege sich das auch selbst ):
Erst wer das verstanden hat, hat die SRT w i r k l i c h verstanden.
Beste Grüße,
grtgrt
An Okotombrok, Eugen, Henry, Horst und Stueps:
Euch scheint nicht bewusst zu sein, dass die SRT — anders als die ART —
- gar nicht darüber spricht, wie schnell ein Objekt a l t e r t ,
- sondern n u r darüber, wie schnell andere, zu ihm gleichförmig bewegte Objekte es altern s e h e n.
Und speziell für Horst, sei gesagt, dass das Wort "sehen" hier nicht allzu wörtlich verstanden werden darf:
Es steht für "sehen könnten unter der Voraussetzung, dass jedes Objekt die Fähigkeit hat, beliebig weit absolut genau zu sehen".
In moderner Terminologie kann man das Szenario, in dem die SRT argumentiert, ohne Beschränkung der Allgemeinheit beschreiben wie folgt:
- Betrachtet wird ein 3-dimensionaler Raum, in dem sich Personen (sog. Beobachter) befinden.
- Jeder Beobachter trägt eine Uhr mit sich, und all diese Uhren sind von absolut gleicher Bauart.
- Jeder Beobachter X hat einen PC, dessen Bildschirm stets zwei Uhren zeigt: Die eigene und die eines anderen Beobachters Y.
- Jede Uhr sendet bei jedem ihrer Ticks ein Signal aus, welches all diese Computer empfangen und so die auf ihren Bildschirmen gezeigten Uhrenbilder aktualisieren.
- Der Zeitbegriff eines Beobachters X ist stets der, den das Bild seiner e i g e n e n Uhr ihm erzeugt.
- Zeit (in diesem Sinne) sieht X als eine vierte Dimension des Raumes, in dem er und alle anderen existieren.
- Wo zwei Beobachter sich relativ zueinander bewegen, geschieht dies mit konstanter Geschwindigkeit v < c.
KONSEQUENZ all dessen ist ( jeder überlege sich das auch selbst ):
- Genau dann, wenn zwei Beobachter sich voneinander entfernen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen l a n g s a m e r gehen als seine eigene (der Endlichkeit der Signalgeschwindigkeit wegen).
- Genau dann, wenn zwei Beobachter sich auf einander zu bewegen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen s c h n e l l e r gehen als seine eigene (wieder der Endlichkeit der Signalgeschwindigkeit wegen).
Beste Grüße,
grtgrt
Beitrag 1997-114
-
Hi Eugen,
ich folgere daraus, dass für diesen Fall nur die ART — aber nicht die SRT — zutreffende Vorhersagen die W i r k l i c h k e i t betreffend macht:
FAZIT also: Die ART beschreibt die Wirklichkeit, die SRT beschreibt nur Unterschiede beobachterspezifischer S i c h t e n .
Gruß, grtgrt
Bauhof in 1997-113:Grtgrt in 1997-111:
KONSEQUENZ all dessen ist ( jeder überlege sich das auch selbst ):
- Genau dann, wenn zwei Beobachter sich voneinander entfernen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen l a n g s a m e r gehen als seine eigene (der Endlichkeit der Signalgeschwindigkeit wegen).
- Genau dann, wenn zwei Beobachter sich auf einander zu bewegen, sieht jeder auf seinem Bildschirm die Uhr des jeweils anderen s c h n e l l e r gehen als seine eigene (wieder der Endlichkeit der Signalgeschwindigkeit wegen).
Hallo Grtgrt,
ok, und was folgerst du daraus für das Einsteinsche Zwillings-Experiment:
Zitat:Ein Zwilling bleibt auf der Erde, der andere Zwilling reist mit 80% der Lichtgeschwindigkeit zu einem anderen Stern, kehrt dort um und reist zur Erde zurück.
Sind nach der Rückkehr des reisenden Zwillings beide Zwillinge gleich alt oder nicht gleich alt?
M.f.G. Eugen Bauhof
Hi Eugen,
ich folgere daraus, dass für diesen Fall nur die ART — aber nicht die SRT — zutreffende Vorhersagen die W i r k l i c h k e i t betreffend macht:
- Die ART berücksichtigt, dass zum Verlassen der Erde ebenso wie zur Umkehr, ebenso wie beim letzten Abbremsen (bevor man auf der Erde wieder zum Stillstand kommt) Beschleunigungskräfte wirken, denen der eine ausgesetzt, der andere aber nicht ausgesetzt ist. Sie bewirken, dass die beiden unterschiedlich schnell altern und daher — wenn sie sich wieder die Hand schütteln können — tatsächlich unterschiedlich alt sein werden,
- Die SRT ignoriert all das und sagt uns, dass der Altersunterschied, den die beiden während des Experiments beobachten, zunächst ansteigt und sich dann wieder reduziert bis hin zu Null. Und das kann gar nicht anders sein, denn nach der SRT ist die Sicht von X auf Y exakt dieselbe wie die von Y auf X. Das gilt s t e t s (und gilt deswegen auch noch in dem Moment, in dem sie sich wieder treffen. Somit kann dann auch keiner von beiden älter sein als der jeweils andere (!).
FAZIT also: Die ART beschreibt die Wirklichkeit, die SRT beschreibt nur Unterschiede beobachterspezifischer S i c h t e n .
Gruß, grtgrt
Beitrag 1997-121
-
Hi Stueps,
der Wikipedia-Artikel, den Du da nennst, berugt zum großen Teil auf einem (dort auch zitierten) Artikel von Mike Bernhardt: Zum Zwillingsparadoxon in der Speziellen Relativitätstheorie. Schon auf der ersten Seite dieses Papiers aber steht:
Mit anderen Worten:
Nun, wo Fachleute zu unterschiedlichem Ergebnis kommen, weiß der Laie nicht, welche Gruppe recht hat. Er muss deswegen seinen eigenen Verstand bemühen. Genau das habe ich getan — und siehe da: Ich stelle fest, dass W. Greiner und J. Rafelski recht haben.
Es wundert mich nicht, dass meine Überlegungen die dieser beiden anerkannten Physikprofessoren bestätigen (und nicht die von Mike Bernhardt, der — soweit ich per Wikipedia feststellen konnte — wohl nur wissenschaftlicher Assistent ist).
Beste Grüße,
Gebhard
Es freut mich, dass hier bestätigt wird: Wo namenlose Physiker anderer Meinung sind als ein namenloser Mathematiker (wie ich etwa), kann man der Logik des Mathematikers mindestens so viel zutrauen wie der des Physikers — selbst dann, wenn es um eine physikalische Frage geht.
Nette Beobachtung nebenbei: Bernhardt hat auf dreierlei verschiedene Weise gerechnet und kam auf allen 3 Wegen — wie er selbst noch auf Seite 1 seine Papiers stolz berichtet — zum gleichen Ergebnis (!).
Stueps in 1997-117:schon der Wikipedia-Artikel begründet ausreichend, warum Gebhard mit Beitrag 1997-114 komplett falsch liegt.
Das ist sogar für mich ersichtlich.
Grüße
Hi Stueps,
der Wikipedia-Artikel, den Du da nennst, berugt zum großen Teil auf einem (dort auch zitierten) Artikel von Mike Bernhardt: Zum Zwillingsparadoxon in der Speziellen Relativitätstheorie. Schon auf der ersten Seite dieses Papiers aber steht:
Zitat von Mike Bernhardt:
Einige Autoren3 gehen in ihrer Argumentation allerdings ... weiter und sagen, dass wegen dieser Beschleunigungen die Spezielle Relativitatstheorie gar nicht angewendet werden dürfe, da es sich nicht mehr um Inertialsysteme handele, und dass stattdessen zur Erklarung des Zwillingsparadoxons die Allgemeine Relativitatstheorie herangezogen werden müsse. Dieses Argument kann aber ad absurdum gefuhrt werden, wenn man das Zwillingsparadoxon so abwandelt, dass keine Beschleunigungen mehr vorkommen.
Quelle3: W. Greiner, J. Rafelski, Spezielle Relativitätstheorie, Verlag Harri Deutsch, 1989
Mit anderen Worten:
- Mike Bernhardt (und der von ihm abschreibende Autor der Wikipedia-Seite) sind e u r e r Ansicht,
- Die Buchautoren W. Greiner und J. Rafelski aber geben m i r recht.
Nun, wo Fachleute zu unterschiedlichem Ergebnis kommen, weiß der Laie nicht, welche Gruppe recht hat. Er muss deswegen seinen eigenen Verstand bemühen. Genau das habe ich getan — und siehe da: Ich stelle fest, dass W. Greiner und J. Rafelski recht haben.
Es wundert mich nicht, dass meine Überlegungen die dieser beiden anerkannten Physikprofessoren bestätigen (und nicht die von Mike Bernhardt, der — soweit ich per Wikipedia feststellen konnte — wohl nur wissenschaftlicher Assistent ist).
Beste Grüße,
Gebhard
Es freut mich, dass hier bestätigt wird: Wo namenlose Physiker anderer Meinung sind als ein namenloser Mathematiker (wie ich etwa), kann man der Logik des Mathematikers mindestens so viel zutrauen wie der des Physikers — selbst dann, wenn es um eine physikalische Frage geht.
Nette Beobachtung nebenbei: Bernhardt hat auf dreierlei verschiedene Weise gerechnet und kam auf allen 3 Wegen — wie er selbst noch auf Seite 1 seine Papiers stolz berichtet — zum gleichen Ergebnis (!).
Beitrag 1997-127
-
Hi Stueps,
der logische Fehler, der Bernhardt mit dieser seiner (fett gedruckten) Aussage unterläuft, besteht darin, anzunehmen, dass es möglich wäre, das Zwillingsparadoxon auch in W i r k l i c h k e i t so abzuwandeln, dass es zu keinerlei Beschleunigungskräften mehr kommt. Leider geht das aber gar nicht.
Nebenbei: Es scheint Bernhardt nicht gelungen zu sein, seinen Artikel in einer anerkannten (peer-reviewed) Fachzeitschrift zu veröffentlichen. Selbst in arXiv.org, wo man heute die Erstversionen praktisch aller Artikel der Physiker findet, ist dieser Artikel Bernhardts nicht abgelegt.
Gruß, grtgrt
Stueps in 1997-124:1aus Beitrag 1997-121:
Zitat:Zitat von Mike Bernhardt:
Einige Autoren gehen in ihrer Argumentation allerdings ... weiter und sagen, dass wegen dieser Beschleunigungen die Spezielle Relativitatstheorie gar nicht angewendet werden dürfe, da es sich nicht mehr um Inertialsysteme handele, und dass stattdessen zur Erklarung des Zwillingsparadoxons die Allgemeine RelatiÂvitatstheorie herangezogen werden müsse. Dieses Argument kann aber ad absurdum gefuhrt werden, wenn man das Zwillingsparadoxon so abwandelt, dass keine Beschleunigungen mehr vorkommen.
Hi Stueps,
der logische Fehler, der Bernhardt mit dieser seiner (fett gedruckten) Aussage unterläuft, besteht darin, anzunehmen, dass es möglich wäre, das Zwillingsparadoxon auch in W i r k l i c h k e i t so abzuwandeln, dass es zu keinerlei Beschleunigungskräften mehr kommt. Leider geht das aber gar nicht.
Nebenbei: Es scheint Bernhardt nicht gelungen zu sein, seinen Artikel in einer anerkannten (peer-reviewed) Fachzeitschrift zu veröffentlichen. Selbst in arXiv.org, wo man heute die Erstversionen praktisch aller Artikel der Physiker findet, ist dieser Artikel Bernhardts nicht abgelegt.
Gruß, grtgrt
Beitrag 1997-134
-
Hallo Eugen,
erst mal vielen Dank für Deine Mühe. Ich weiß sie sehr zu schätzen!
Nun aber lass mich dazu Stellung beziehen (Ausgangspunkt können heute nur die Zitate selbst sein, denn keines jener Bücher habe ich zu Hause):
Zunächst mal ist festzustellen, dass wir beide hier etwas sehr Interessantes entdeckt haben:
Die unterschiedliche Überzeugung, die hier im Forum die beiden Gruppen an Physik interessierter Laien
{ Bauhof, Stueps, Henry, Okotombrok } vs { Grtgrt, Harti }
auseinander dividiert, besteht offenbar auch zwischen den beiden folgenden Gruppen von Physik-Professoren:
{ D.Giulini & T.Filk + C.Kiefer + E.Rebhan } vs { W.Greiner & J.Rafelski }.
Um zu sehen, wer recht hat, müssen wir jetzt also tatsächlich die Argumentation aller viel genauer als bisher betrachten, um zu sehen, wo die eine oder andere lückenhaft oder nicht nachvollziehbar ist. Tun wir das:
Allen — den Professoren ebenso wie uns hier im Forum — ist gemeinsam, dass wir wissen: Wo die Situation, die zum sog. Zwillingsparadoxon führt (kurz: SZw), in der Wirklichkeit nachgestellt wird, werden die beiden Zwillinge mindestens zeitweise unterschiedlichen Beschleunigungskräften ausgesetzt sein. Schon allein deswegen wird jeder Logiker uns sagen: Da die SRT Situationen, in denen es zu beschleunigter Bewegung kommt, gar nicht vorgibt, noch behandeln zu können, kann sie auf Situation SZw auch gar nicht anwendbar sein.
Nun könnte man aber argumentieren, dass die SRT, wenn man genauer hinsieht, vielleicht auch beschleunigte Situationen noch behandeln könnte (dass also Einstein und Minkowski, die Einschränkung, nur gleichförmige Bewegung zuzulassen, vielleicht gar nicht hätten machen müssen).
Jeder, der behauptet, auch die SRT würde beweisen, dass die Zwillinge, wenn sie sich wieder treffen, unterschiedlich alt sind, geht — implizit oder explizit — von dieser Annahme aus — hat dann aber auch die Pflicht, sie zu beweisen.
Die Zitate [1] und [2] skizzieren den Ansatz solcher Beweisversuche, sind aber nicht detailliert genug, mir zu zeigen, ob jene "Beweise" auch wirklich schlüssig sind.
Im Zitat [3] wird durch Rebhan explizit versucht, die SRT so zu erweitern, dass sie auch noch auf beschleunigte Bewegung anwendbar ist. Dies, so wird behauptet, gelänge über Anwendung eines mathematischen Grenzprozesses. Zwei Aussagen aus diesem Beweisversuch aber finde ich nicht wirklich nachvollziebar. Es sind die jetzt im Zitat rot hervorgehobenen Teile:
Zitat [4] schließlich begündet die Meinung der Autoren nur in Form einer (als "offensichtlich wahr" hingestellten) V e r m u t u n g (und ist deswegen nicht ernst zu nehmen. Die Autoren scheinen Gymnasiallehrer zu sein, Personen also, die wohl auch nicht kompetenter sind als an Relativitätstheorie ernsthaft interessierte Laien.
Dem Zitat aus [5] schließlich kann ich gar nicht entnehmen, dass der Autor — Ulrich Schröder — es für zweifelsfrei erwiesen hält, dass die SRT auf die Situation beschleunigter Bewegung in irgendeiner sinnvollen Verallgemeinerung ihrer selbst (der SRT) anwendbar wird. Er weist lediglich mit Bestimmheit darauf hin, dass in der realen Wirklichkeit unser Welt (wie Hafele & Keating zeigen konnten) es tatsächlich zu unterschiedlich schneller Alterung zweier Objekte kommen kann.
[1] Giulini, Domenico und Filk, Thomas: Am Anfang war die Ewigkeit. Auf der Suche nach dem Ursprung der Zeit.
München 2004
ISBN=3-406-52187-8
[2] Kiefer, C...: Der Quantenkosmos.
Frankfurt am Main 2008
ISBN=978-3-10-039506-1
[3] Rebhan, Eckhard: Theoretische Physik. Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999
ISBN=3-8274-0246-8
[4] Beyvers, Gottfried und Kusch, Elvira: Kleines 1 x 1 der Relativitätstheorie. Einsteins Physik mit Mathematik der Mittelstufe.
Berlin 2009
ISBN=978-3-540-85202-5
[5] Schröder, Ulrich E.: Spezielle Relativitätstheorie (Vierte Auflage)
Frankfurt am Main 2005
ISBN=3-8171-1724-8
Wenn wir uns jetzt im Gegenzug auch mein Argument aus Beitrag 1997-114 nochmals vornehmen, so wird klar:
Meine Argumentation benötigt, um gültig zu sein, nur eine einzige Voraussetzung:
Die Konstanz und Endlichkeit der Lichtgeschwindigkeit.
Sie ist deswegen sogar noch auf beschleunigte Bewegungen anwendbar und zwar ganz unabhängig davon, ob beide Zwillinge oder nur einer beschleunigt wird.
So lange mir also in eben dieser Argumentation niemand einen Fehler aufzeigen kann, sehe ich sie als wunderbar einfache Bestätigung der Meinung von W.Greiner und J.Rafelski.
Auch wenn man nachsieht, wie renommiert die einzelnen Professoren sind, stehen da W.Greiner & J.Rafelski mit Sicherheit an der Spitze.
Damit, Eugen, bleibt mir vernünftiger Weise gar nichts anderes übrig, als zunächst mal zu glauben, dass diese beiden — und damit auch ich — recht haben.
Mit besten Grüßen,
Gebhard (grtgrt)
Hallo Harti,
auch nachdem Okotombrok das Thema 1997 für jede weitere Äußerung gesperrt hat, bin ich der Frage, ob das Zwillingsparadoxon per SRT lösbar ist, weiter nachgegangen und weiß nun, dass Du und ich — aber dennoch auch die anderen — recht hatten.
Es gilt nämlich:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch zutreffende Aussagen darüber machen kann, wie Beschleunigung sich auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche auf dem Hintergrund der Raumzeit der SRT errechneten Ergebnisse tatsächlich (grob wenigstens) mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrunde liegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt zudem sehr klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
ausschließlich auf jene Phasen der Reise zurückführt, in denen die beiden Zwillinge unterschiedlich beschleunigt waren.
Damit steht fest:
Hierbei allerdings muss berücksichtigt werden:
Diesen wesentlichen Unterschied nicht zu übersehen, macht es schon Sinn, über beschleunigte Bewegungen tatsächlich nur mit Hilfe der ART nachzudenken. Siehe dazu auch Bemerkungen auf gutefrage.net.
Man sieht hier sehr schön, dass unterschiedlich genaue physikalische Modelle — SRT und ART — eben auch unterschiedlich genaue Aussagen machen.
Beste Grüße,
grtgrt
Bauhof in 1997-122:
Grtgrt in 1997-121:Hi Eugen,
wenn du mir Links auf jene Stellen geben kannst — oder sie in Büchern zu finden sind, auf die ich Zugriff habe — werde ich sie mir ganz bestimmt ansehen.
Hallo Grtgrt,
gut, ich mache mir mal die Mühe und gebe dir die entsprechenden Hinweise als Zitate aus meinen Büchern. Keiner der aufgeführten Autoren gibt einen Hinweis darauf, dass das Zwillingsparadoxon nur mit Hilfe der ART gelöst werden könnte. Sie argumentieren alle mit Hilfe der SRT.
Hallo Eugen,
erst mal vielen Dank für Deine Mühe. Ich weiß sie sehr zu schätzen!
Nun aber lass mich dazu Stellung beziehen (Ausgangspunkt können heute nur die Zitate selbst sein, denn keines jener Bücher habe ich zu Hause):
Zunächst mal ist festzustellen, dass wir beide hier etwas sehr Interessantes entdeckt haben:
Um zu sehen, wer recht hat, müssen wir jetzt also tatsächlich die Argumentation aller viel genauer als bisher betrachten, um zu sehen, wo die eine oder andere lückenhaft oder nicht nachvollziehbar ist. Tun wir das:
Allen — den Professoren ebenso wie uns hier im Forum — ist gemeinsam, dass wir wissen: Wo die Situation, die zum sog. Zwillingsparadoxon führt (kurz: SZw), in der Wirklichkeit nachgestellt wird, werden die beiden Zwillinge mindestens zeitweise unterschiedlichen Beschleunigungskräften ausgesetzt sein. Schon allein deswegen wird jeder Logiker uns sagen: Da die SRT Situationen, in denen es zu beschleunigter Bewegung kommt, gar nicht vorgibt, noch behandeln zu können, kann sie auf Situation SZw auch gar nicht anwendbar sein.
Nun könnte man aber argumentieren, dass die SRT, wenn man genauer hinsieht, vielleicht auch beschleunigte Situationen noch behandeln könnte (dass also Einstein und Minkowski, die Einschränkung, nur gleichförmige Bewegung zuzulassen, vielleicht gar nicht hätten machen müssen).
Jeder, der behauptet, auch die SRT würde beweisen, dass die Zwillinge, wenn sie sich wieder treffen, unterschiedlich alt sind, geht — implizit oder explizit — von dieser Annahme aus — hat dann aber auch die Pflicht, sie zu beweisen.
Die Zitate [1] und [2] skizzieren den Ansatz solcher Beweisversuche, sind aber nicht detailliert genug, mir zu zeigen, ob jene "Beweise" auch wirklich schlüssig sind.
Im Zitat [3] wird durch Rebhan explizit versucht, die SRT so zu erweitern, dass sie auch noch auf beschleunigte Bewegung anwendbar ist. Dies, so wird behauptet, gelänge über Anwendung eines mathematischen Grenzprozesses. Zwei Aussagen aus diesem Beweisversuch aber finde ich nicht wirklich nachvollziebar. Es sind die jetzt im Zitat rot hervorgehobenen Teile:
Zitat:
Wir betrachten noch die kurzen Beschleunigungsphasen der Rakete im Inertialsystem der Erde. Diese können wir stückweise aus Teilen zusammensetzen, während deren die Geschwindigkeit annähernd konstant ist. Da diese jeweils kleiner als die Fluggeschwindigkeit v ist, ergibt sich für die Dauer einer ganzen Beschleunigungsphase im Mittel eine kleinere Zeitdilatation als für eine gleich lange Flugphase mit der konstanten Reisegeschwindigkeit. Lassen wir jetzt die Beschleunigung gegen unendlich und die Beschleunigungsdauer gegen null gehen, so geht auch die diktierte Beschleunigungsdauer gegen null.
Man könnte vermuten, dass dem Effekt der SRT auch noch Effekte der ART überlagert sind. Wir werden später allerdings sehen, dass das nur der Fall ist, wenn Schwerefelder involviert sind, ansonsten bleibt die oben angestellte Überlegung richtig. Man kann sich aber auch schon, ohne Genaueres über ART-Effekt zu wissen, darüber klar werden, dass diese bei einer langen Raumfahrt keine Rolle spielen. Um das einzusehen, nehmen wir an, für den Zwilling auf der Erde sei die Dauer einer Beschleunigungsphase dt, für den im Raumschiff unter Einbezug von ART-Effekten dt'. Aus der Homogenität der Zeit folgt, dass der Quotient dt'/dt nur von der Art des Beschleunigungsprozesses abhängt, nicht aber von dem Zeitpunkt, zu dem er durchgeführt wird. Die Raumfahrt enthält vier gleichartige Beschleunigungsprozesse, die Geschwindigkeit des Raumschiffes geht von
0 → vmax → 0 → vmax → 0
Damit ergibt sich als Altersunterschied der Zwillinge
D = ( T – T' ) + 4( dt – dt' )
Der Anteil ( T – T' ) wächst mit der Dauer der Raumfahrt, während der Anteil 4( dt – dt' ) konstant ist. Er kann durch ein Differenzexperiment zum Verschwinden gebracht werden; in einem Einzelexperiment wird er vernachlässigbar, wenn die Raumfahrt hinreichend lange dauert. Für unsere weiteren Überlegungen machen wir die letzte Annahme.
Zitat [4] schließlich begündet die Meinung der Autoren nur in Form einer (als "offensichtlich wahr" hingestellten) V e r m u t u n g (und ist deswegen nicht ernst zu nehmen. Die Autoren scheinen Gymnasiallehrer zu sein, Personen also, die wohl auch nicht kompetenter sind als an Relativitätstheorie ernsthaft interessierte Laien.
Dem Zitat aus [5] schließlich kann ich gar nicht entnehmen, dass der Autor — Ulrich Schröder — es für zweifelsfrei erwiesen hält, dass die SRT auf die Situation beschleunigter Bewegung in irgendeiner sinnvollen Verallgemeinerung ihrer selbst (der SRT) anwendbar wird. Er weist lediglich mit Bestimmheit darauf hin, dass in der realen Wirklichkeit unser Welt (wie Hafele & Keating zeigen konnten) es tatsächlich zu unterschiedlich schneller Alterung zweier Objekte kommen kann.
[1] Giulini, Domenico und Filk, Thomas: Am Anfang war die Ewigkeit. Auf der Suche nach dem Ursprung der Zeit.
München 2004
ISBN=3-406-52187-8
[2] Kiefer, C...: Der Quantenkosmos.
Frankfurt am Main 2008
ISBN=978-3-10-039506-1
[3] Rebhan, Eckhard: Theoretische Physik. Band 1: Mechanik, Elektrodynamik, Spezielle und Allgemeine Relativitätstheorie, Kosmologie
Heidelberg 1999
ISBN=3-8274-0246-8
[4] Beyvers, Gottfried und Kusch, Elvira: Kleines 1 x 1 der Relativitätstheorie. Einsteins Physik mit Mathematik der Mittelstufe.
Berlin 2009
ISBN=978-3-540-85202-5
[5] Schröder, Ulrich E.: Spezielle Relativitätstheorie (Vierte Auflage)
Frankfurt am Main 2005
ISBN=3-8171-1724-8
Wenn wir uns jetzt im Gegenzug auch mein Argument aus Beitrag 1997-114 nochmals vornehmen, so wird klar:
Die Konstanz und Endlichkeit der Lichtgeschwindigkeit.
Sie ist deswegen sogar noch auf beschleunigte Bewegungen anwendbar und zwar ganz unabhängig davon, ob beide Zwillinge oder nur einer beschleunigt wird.
So lange mir also in eben dieser Argumentation niemand einen Fehler aufzeigen kann, sehe ich sie als wunderbar einfache Bestätigung der Meinung von W.Greiner und J.Rafelski.
Auch wenn man nachsieht, wie renommiert die einzelnen Professoren sind, stehen da W.Greiner & J.Rafelski mit Sicherheit an der Spitze.
Damit, Eugen, bleibt mir vernünftiger Weise gar nichts anderes übrig, als zunächst mal zu glauben, dass diese beiden — und damit auch ich — recht haben.
Mit besten Grüßen,
Gebhard (grtgrt)
Harti in Beitrag Nr. 1197-119:
Hallo Grtgrt,
lass Dich durch das Etikett "Einstein-Widerleger" nicht ins Boxhorn jagen. Selbstverständlich kann man das Zwillingsparadoxon nur mit Hilfe der ART lösen.
Hallo Harti,
auch nachdem Okotombrok das Thema 1997 für jede weitere Äußerung gesperrt hat, bin ich der Frage, ob das Zwillingsparadoxon per SRT lösbar ist, weiter nachgegangen und weiß nun, dass Du und ich — aber dennoch auch die anderen — recht hatten.
Es gilt nämlich:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch zutreffende Aussagen darüber machen kann, wie Beschleunigung sich auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche auf dem Hintergrund der Raumzeit der SRT errechneten Ergebnisse tatsächlich (grob wenigstens) mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrunde liegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt zudem sehr klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
Damit steht fest:
- Wer von der SRT (in Einsteins Fassung) ausgeht, geht von einer Theorie aus, die zu beschleunigten Bewegungen nichts aussagen will und demnach auf die Situation des Zwillingsparadoxon gar nicht anwendbar ist.
- Seit etwa 2000 aber geht man nicht mehr davon aus, dass die SRT — wenn man versucht, sie auch auf beschleunigte Bewegung anzuwenden — falsche Aussagen macht. Soweit man nämlich Beispiele in SRT u n d ART durchgerechnet hat, kam man zum gleichen Ergebnis (was aber nicht heißt, dass wirklich alles, was die ART sagt, auch mit Mitteln der SRT nachrechenbar wäre).
- Es kommt hier wohl die Tatsache zum Tragen, dass in jeder hinreichend kleinen Umgebung eines nicht singulären Punktes P der Raumzeit der ART die SRT sehr gute Approximation der ART ist.
Hierbei allerdings muss berücksichtigt werden:
-
Wer im Rahmen der SRT auch beschleunigte Bewegungen betrachtet, sieht die Beschleunigung einfach nur als erste Ableitung der Geschwindigkeit nach der Zeit —
er sieht sie dann also noch nicht — wie die ART es tut — auch als physikalisches Phänomen äquivalent zu einer Krümmung der Raumzeit.
Diesen wesentlichen Unterschied nicht zu übersehen, macht es schon Sinn, über beschleunigte Bewegungen tatsächlich nur mit Hilfe der ART nachzudenken. Siehe dazu auch Bemerkungen auf gutefrage.net.
Man sieht hier sehr schön, dass unterschiedlich genaue physikalische Modelle — SRT und ART — eben auch unterschiedlich genaue Aussagen machen.
Beste Grüße,
grtgrt
Beitrag 1997-139
-
Hallo Eugen,
wie ich schon in meinem Beitrag 1997-121 schrieb, wird die Tatsache, dass Greiner & Rafelski so argumentieren, von Mike Bernhardt selbst in seiner Schrift » Zum Zwillingsparadoxon in der Speziellen Relativitätstheorie « explizit erwähnt.
Er tut das gleich auf Seite 1 seines Artikels, um uns zu sagen, dass er selbst anderer Ansicht ist. Diese andere — von Greiner & Rafelski abweichende — Ansicht zu begründen, dienen die Rechnungen in seinem Papier (die dann allerdings unter der Nebenbedingung ausgeführt werden, dass es möglich sei, das Zwillingsparadoxon so abzuwandeln, dass keine Beschleunigungen mehr vorkommen).
Dass ich auf das Buch von Greiner & Rafelski, auf das Berhardt da Bezug nimmt, nicht im Zugriff habe, kann man mir ja wohl nicht vorwerfen. Aber vielleicht ist es ja dir zugänglich?
Gruß,
grtgrt
Bauhof in 1997-138:
Hallo Gebhard,
tut mit leid, diese Gegenüberstellung kann ich nicht anerkennen.
Von Greiner und Rafelski habe ich bisher von dir keinen einzigen Textauszug aus ihren Büchern gesehen. Ich vermute, du besitzt diese Bücher gar nicht.
Hallo Eugen,
wie ich schon in meinem Beitrag 1997-121 schrieb, wird die Tatsache, dass Greiner & Rafelski so argumentieren, von Mike Bernhardt selbst in seiner Schrift » Zum Zwillingsparadoxon in der Speziellen Relativitätstheorie « explizit erwähnt.
Er tut das gleich auf Seite 1 seines Artikels, um uns zu sagen, dass er selbst anderer Ansicht ist. Diese andere — von Greiner & Rafelski abweichende — Ansicht zu begründen, dienen die Rechnungen in seinem Papier (die dann allerdings unter der Nebenbedingung ausgeführt werden, dass es möglich sei, das Zwillingsparadoxon so abzuwandeln, dass keine Beschleunigungen mehr vorkommen).
Dass ich auf das Buch von Greiner & Rafelski, auf das Berhardt da Bezug nimmt, nicht im Zugriff habe, kann man mir ja wohl nicht vorwerfen. Aber vielleicht ist es ja dir zugänglich?
Gruß,
grtgrt
Beitrag 1997-149
-
Hallo Gebhard,
Max Born nannte diese spezielle nichteuklidische Geometrie im Minkowski-Raum pseudo-euklidischen Geometrie. Er schreibt dazu auf Seite 192 seines Buches [1] folgendes:
Meine mathematischen Kenntnisse sind leider bei weitem nicht ausreichend, um Minkowskis Vektor- und Tensor-Rechnung für die pseudo-euklidische Geometrie zu studieren [2]. Kannst du uns als Mathematiker nahe bringen, um was es da geht?
[1] Born, Max
Physik im Wandel meiner Zeit.
Braunschweig 1983
ISBN=3-528-08539-8
[2] Harti natürlich schüttelt so etwas mühelos aus dem Ärmel :lol:
Gesunder Menschenverstand:
Eine Sammlung von Vorurteilen, die man bis zum
achtzehnten Lebensjahr erworben hat.
Albert Einstein
Hallo Gebhard,
Max Born nannte diese spezielle nichteuklidische Geometrie im Minkowski-Raum pseudo-euklidischen Geometrie. Er schreibt dazu auf Seite 192 seines Buches [1] folgendes:
Zitat:Minkowski veröffentlichte seine Arbeit "Die Grundlagen für die elektromagnetischen Vorgänge in bewegten Körpern" im Jahre 1907. Sie enthält eine systematische Darstellung seiner formalen Verschmelzung von Raum und Zeit zu einer vierdimensionalen "Welt" mit einer pseudo-euklidischen Geometrie, für die er eine Vektor- und Tensor-Rechnung entwickelte.
Dieser Kalkül wurde mit gewissen Abänderungen bald die allgemein gebrauchte Methode aller relativistischen Untersuchungen. Darüber hinaus enthält Minkowskis Arbeit wichtige neue Ergebnisse: ein System von elektromagnetischen Feldgleichungen in bewegter Materie, das gegenüber Lorentz-Transformationen exakt invariant ist, nicht nur in erster Näherung, wie Lorentz’ eigene, ein wenig abweichende Gleichungen; ferner einen neuen Weg zur Ableitung der mechanischen Bewegungsgleichungen.
Meine mathematischen Kenntnisse sind leider bei weitem nicht ausreichend, um Minkowskis Vektor- und Tensor-Rechnung für die pseudo-euklidische Geometrie zu studieren [2]. Kannst du uns als Mathematiker nahe bringen, um was es da geht?
[1] Born, Max
Physik im Wandel meiner Zeit.
Braunschweig 1983
ISBN=3-528-08539-8
[2] Harti natürlich schüttelt so etwas mühelos aus dem Ärmel :lol:
Signatur:
Eine Sammlung von Vorurteilen, die man bis zum
achtzehnten Lebensjahr erworben hat.
Albert Einstein
Beitrag zuletzt bearbeitet von Bauhof heute, 14:52 Uhr.
Beitrag 1997-150
-
Hallo Eugen,
leider habe ich mich während meiner Zeit als Student oder als aktiv forschender Mathematiker nie mit Metriken befasst, die nicht-euklidische Geometrie erzeugen. Aus dem Ärmel schütteln kann ich die gewünsche Erklärung also nicht.
Auf deine Anregung hin werde ich aber versuchen, mich da schlau zu machen, um dann hier im Forum tatsächlich eine Antwort auf deine Frage präsentieren zu können.
Es kann aber etwas dauern, bis ich genügend zeitlichen Spielraum dafür finde ...
Bis dann also,
mit besten Grüßen,
grtgrt
Bauhof in 1997-149:
Meine mathematischen Kenntnisse sind leider bei weitem nicht ausreichend, um Minkowskis Vektor- und Tensor-Rechnung für die pseudo-euklidische Geometrie zu studieren [2�. Kannst du uns als Mathematiker nahe bringen, um was es da geht?
Hallo Eugen,
leider habe ich mich während meiner Zeit als Student oder als aktiv forschender Mathematiker nie mit Metriken befasst, die nicht-euklidische Geometrie erzeugen. Aus dem Ärmel schütteln kann ich die gewünsche Erklärung also nicht.
Auf deine Anregung hin werde ich aber versuchen, mich da schlau zu machen, um dann hier im Forum tatsächlich eine Antwort auf deine Frage präsentieren zu können.
Es kann aber etwas dauern, bis ich genügend zeitlichen Spielraum dafür finde ...
Bis dann also,
mit besten Grüßen,
grtgrt
Beitrag 1997-80
Erst unterschiedlich beschleunigt zu werden gibt Zwillingen unterschiedliches Alter (?)
Beschleunigung — und wirklich nur sie — dehnt Eigenzeit
Hallo Henry,
diese Aussage Müllers ist richtig — aber eben n u r wegen der Vergröberung, mit der sie formuliert ist. Diese Vergröberung (ein Ausblenden wirklich wichtiger Details) besteht darin, dass diese Formulierung den qualitativen Unterschied zwischen der Raumzeit einerseits und beobachterspezifischen S i c h t e n darauf andererseits völlig ignoriert.
Tatsache ist:
Eine Dilation der Zeit und zu ihr korrelierte Kontraktion von Längen gibt es NUR im Sinne der S i c h t e n ,
aber keineswegs im Sinne der Struktur der Raumzeit (der SRT) selbst.
Dass dem wirklich so ist, erkennt man sehr schön, wenn man sich zwei Personen X und Y vorstellt, die sich mit gleichförmiger Geschwindigkeit zuerst voneinander entfernen um dann, wenn jeder den jeweils anderen in einer Entfernung von genau 100 km vermutet, mit eben derselben Geschwindigkeit wieder aufeinander zuzufliegen.
Bitte beachte:
Wir sehen also: Das Zwillingsparadoxon gibt es n u r in der Raumzeit der ART, aber n i c h t in der Raumzeit der SRT.
In der SRT sind beobachtete Unterschiede wirklich n u r darauf zurückzuführen, dass Beobachter, die solche Unterschiede feststellen, aus unterschiedlichen Bezugssystemen heraus argumentieren.
In der ART dageben kommt unterschiedliches Altern der Zwillinge durchaus zustande, da hier auch die für beide Personen unterschiedlichen Beschleunigungen mit berücksichtigt werden: eine Art von Kraftwirkung also, die die SRT gar nicht erst zu betrachten versucht.
Gruß,
grtgrt
PS: Eine erweiterte, über Einstein hinausgehende Form der SRT löst das Zwillingsparadoxon dennoch. Genauer:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch Aussagen darüber machen kann, wie sich Beschleunigung auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche Ergebnisse tatsächlich mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrundeliegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
ausschließlich auf jene Phasen der Reise zurückführt, in denen die beiden Zwillinge unterschiedlich beschleunigt waren.
FAZIT also:
Henry in 1997-67:
Um nicht immer aus Wikipedia zu zitieren:
» Durch Einstein wurde unser Verständnis von Raum und Zeit radikal neu gestaltet: Phänomene wie Zeitdilatation und Lorentz-Kontraktion und die Verschmelzung von Raum und Zeit im Raum-Zeit-Kontinuum sind eine natürliche Konsequenz der Speziellen Relativitätstheorie. «
Ein Zitat aus http://www.wissenschaft-online.de/astrowissen/ von Dr. Andreas Müller.
Der Autor Dr. Andreas Müller ist Astrophysiker und wissenschaftlicher Koordinator im Exzellenzcluster "Origin and Structure of the Universe" der Technischen Universität München.
Hallo Henry,
diese Aussage Müllers ist richtig — aber eben n u r wegen der Vergröberung, mit der sie formuliert ist. Diese Vergröberung (ein Ausblenden wirklich wichtiger Details) besteht darin, dass diese Formulierung den qualitativen Unterschied zwischen der Raumzeit einerseits und beobachterspezifischen S i c h t e n darauf andererseits völlig ignoriert.
Tatsache ist:
aber keineswegs im Sinne der Struktur der Raumzeit (der SRT) selbst.
Dass dem wirklich so ist, erkennt man sehr schön, wenn man sich zwei Personen X und Y vorstellt, die sich mit gleichförmiger Geschwindigkeit zuerst voneinander entfernen um dann, wenn jeder den jeweils anderen in einer Entfernung von genau 100 km vermutet, mit eben derselben Geschwindigkeit wieder aufeinander zuzufliegen.
Bitte beachte:
- Dies ist ein absolut symmetrisches Szenario.
- Aus Sicht der einen Person geht die Uhr der jeweils anderen langsamer,
- und doch werden beide Uhren — wenn die beiden Personen sich wieder treffen — genau gleiche Zeit anzeigen (das folgt aus der Symmetrie des Szenarios und ist deswegen so, weil X und Y dann ja auch wieder dasselbe Bezugssystem haben).
Wir sehen also: Das Zwillingsparadoxon gibt es n u r in der Raumzeit der ART, aber n i c h t in der Raumzeit der SRT.
In der SRT sind beobachtete Unterschiede wirklich n u r darauf zurückzuführen, dass Beobachter, die solche Unterschiede feststellen, aus unterschiedlichen Bezugssystemen heraus argumentieren.
In der ART dageben kommt unterschiedliches Altern der Zwillinge durchaus zustande, da hier auch die für beide Personen unterschiedlichen Beschleunigungen mit berücksichtigt werden: eine Art von Kraftwirkung also, die die SRT gar nicht erst zu betrachten versucht.
Gruß,
grtgrt
PS: Eine erweiterte, über Einstein hinausgehende Form der SRT löst das Zwillingsparadoxon dennoch. Genauer:
Obgleich Einstein selbst im Rahmen der SRT niemals auch beschleunigte Bewegung diskutiert hat, hat man das — so etwa um das Jahr 2000 herum — dennoch versucht und hierbei schnell festgestellt, dass die Lorentztransformation der SRT auch Aussagen darüber machen kann, wie sich Beschleunigung auf das beschleunigte System auswirkt (siehe etwa ein durch Joachim Schulz beschriebenes Gedankenexperiment).
Dass solche Ergebnisse tatsächlich mit denen der ART übereinstimmen, wird — wenigstens für die dem Zwillingsparadoxon zugrundeliegende Situation — explizit nachgerechnet von Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013). Ihre Rechnung auf Seite 111 bis 129 des Buches zeigt klar, dass auch die SRT den für die Zwillinge entstandenen Altersunterschied
FAZIT also:
- Wer von der SRT (in Einsteins Fassung) ausgeht, geht von einer Theorie aus, die zu beschleunigten Bewegungen nichts aussagen will und demnach auf die Situation des Zwillingsparadoxon gar nicht anwendbar ist.
- Seit etwa 2000 aber geht man nicht mehr davon aus, dass die SRT — wenn man versucht, sie auch auf beschleunigte Bewegung anzuwenden — falsche Aussagen macht. Soweit man nämlich Beispiele in SRT u n d ART durchgerechnet hat, kam man zum gleichen Ergebnis (was aber nicht heißt, dass wirklich alles, was die ART sagt, auch mit Mitteln der SRT nachrechenbar wäre).
- Es kommt hier wohl die Tatsache zum Tragen, dass in jeder hinreichend kleinen Umgebung eines nicht singulären Punktes P der Raumzeit der ART die SRT sehr gute Approximation der ART ist.
Beitrag 2102-58
-
Hallo Jense,
Jense in 2102-55:Es kommt auch gleich die nächste Frage:
Ich nehme 2 synchronisierte Uhren.
Wenn ich mich mit einer dieser Uhren für eine Sekunde mit Lichtgeschwindigkeit im Raum bewege, dann müsste diese Uhr im Verhältnis zur unbewegten Uhr 1 Sekunde abweichen, also der synchronisierten Zeit hinterher hinken.
Hallo Jense,
- erstens hat Eugen Bauhof recht mit dem, was er in 2102-57 sagt: Du musst den Passus » mit Lichtgeschwindigkeit « ersetzen durch » mit f a s t Lichtgeschwindigkeit «,
- und zweitens wird, während die beiden Uhren getrennt voneinander unterwegs sind, j e d e die jeweils anders gehen sehen als sich selbst: Langsamer, so lange sie sich voneinander entfernen, und schneller, sobald sie sich wieder aufeinander zu bewegen.
- Sobald sie wieder beisammen sind, werden sie genau dann nicht mehr dieselbe Zeit anzeigen — wird sich also genau dann ein Altersunterschied ergeben haben —, wenn sie zuvor unterschiedlich stark beschleunigt waren. Dies zeigt eine Rechnung von Bernd Sonne und Reinhard Weiß auf den Seiten 111 bis 129 ihres Buches Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013).
Beitrag 2102-65
-
Hallo Eugen,
auf welche Aussage oder Formel in der Arbeitsplattform beziehst Du dich hier?
Meine Meinung ist: Wenn zwei Objekte an zwei Ereignissen E1 und E2 beteiligt sind, dazwischen aber eigene Wege gehen, kann die Länge dieser Wege nur unterschiedlich sein, wenn die beiden Objekte auf ihrem jeweils individuellen Weg unterschiedlich beschleunigt wurden.
Mir ist allerdings nicht klar, ob es dabei nur auf den B e t r a g der Beschleunigung ankommt oder auch auf ihre R i c h t u n g .
Ganz sicher aber bin ich, dass in der Summe gleiche Eigenzeit zwischen E1 und E2 nicht ausschließt, dass die beiden Objekte die eigene Uhr nahezu nie ebenso schnell gehen sehen wie die des Bruders. Die SRT ( im Sinne Einsteins ) spricht nur von dieser jeweils individuellen Sicht — einen sich in der Summe ergebenden wirklichen Altersunterschied, den sie dann beide in E2 feststellen würden, belegt sie n i c h t .
Wer im Rahmen der SRT auch mit beschleunigten Bewegungen umgeht, wird — nach allen Rechnungen, die ich kenne — in E2 nur dann einen Unterschied auch in der
E i g e n z e i t beider Objekte feststellen, wenn sie u n t e r s c h i e d l i c h beschleunigt waren.
Gruß, grtgrt
Bauhof in 2102-60:
Und wenn die Beschleunigungsphasen bei beiden Zwillingen genau gleich lang und gleich stark sind, aber die Länge der Wege durch die Raumzeit aus anderen Gründen unterschiedlich lang sind, dann ergibt sich auch ein Altersunterschied. Siehe dazu die Arbeitsplattform SRT.
Hallo Eugen,
auf welche Aussage oder Formel in der Arbeitsplattform beziehst Du dich hier?
Meine Meinung ist: Wenn zwei Objekte an zwei Ereignissen E1 und E2 beteiligt sind, dazwischen aber eigene Wege gehen, kann die Länge dieser Wege nur unterschiedlich sein, wenn die beiden Objekte auf ihrem jeweils individuellen Weg unterschiedlich beschleunigt wurden.
Ganz sicher aber bin ich, dass in der Summe gleiche Eigenzeit zwischen E1 und E2 nicht ausschließt, dass die beiden Objekte die eigene Uhr nahezu nie ebenso schnell gehen sehen wie die des Bruders. Die SRT ( im Sinne Einsteins ) spricht nur von dieser jeweils individuellen Sicht — einen sich in der Summe ergebenden wirklichen Altersunterschied, den sie dann beide in E2 feststellen würden, belegt sie n i c h t .
Wer im Rahmen der SRT auch mit beschleunigten Bewegungen umgeht, wird — nach allen Rechnungen, die ich kenne — in E2 nur dann einen Unterschied auch in der
E i g e n z e i t beider Objekte feststellen, wenn sie u n t e r s c h i e d l i c h beschleunigt waren.
Gruß, grtgrt
Beitrag 2102-70
-
Hallo Eugen,
an jener Stelle hast Du eine — mir nicht wirklich verständliche — Argumentation stehen, die dich zum Ergebnis führt (Zitat): Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden.
Nun kommen Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013) (siehe dort ihre Rechnung auf den Seiten 111 bis 129) aber zum genau entgegengesetzten Ergebnis.
Das Ergebnis ihrer Rechnung stimmt überein mit einer Berechnung auf Basis ART (die sich erst gegen Ende ihres Buches findet und wesentlich anders ist, wie man aus den Zwischenergebnissen sehen kann). Nachdem diese Übereinstimmung kein Zufall sein kann, vertraue ich ihrer Beweisführung eher als deiner Argumentation.
Mit besten Grüßen,
grtgrt
Bauhof in 2102-68:Hallo Grtgrt,
ich beziehe mich auf die Rubrik "SRT-Glossar", Stichwort "Zwillingsparadoxon".
M.f.G. Eugen Bauhof
Hallo Eugen,
an jener Stelle hast Du eine — mir nicht wirklich verständliche — Argumentation stehen, die dich zum Ergebnis führt (Zitat): Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden.
Nun kommen Bernd Sonne und Reinhard Weiß in ihrem Buch Einsteins Theorien: Spezielle und Allgemeine Relativitätstheorie für interessierte Einsteiger und zur Wiederholung (Springer, 2013) (siehe dort ihre Rechnung auf den Seiten 111 bis 129) aber zum genau entgegengesetzten Ergebnis.
Das Ergebnis ihrer Rechnung stimmt überein mit einer Berechnung auf Basis ART (die sich erst gegen Ende ihres Buches findet und wesentlich anders ist, wie man aus den Zwischenergebnissen sehen kann). Nachdem diese Übereinstimmung kein Zufall sein kann, vertraue ich ihrer Beweisführung eher als deiner Argumentation.
Mit besten Grüßen,
grtgrt
Beitrag 1997-101
-
Okotombrok:
Du denkst einfach nicht weit genug.
Wenn im Beispiel aus Beitrag 1997-80 eine der beiden Personen X und Y — wir dürfen annehmen, es sei X — t a t s ä c h l i c h weniger schnell altern würde als der andere, müsste X — wenn sie sich wieder treffen — jünger sein als Y.
Nach der SRT aber unterscheiden sich die Sichten beider auf den jeweils anderen aber überhaupt nicht. Und deswegen muss, was für X richtig ist, auch für Y richtig sein.
Demzufolge gilt, wenn sie sich wieder treffen,
Alter( X ) ≤ Alter( Y ) ≤ Alter( X )
Das aber kann nur sein, wenn beide nun gleiches Alter haben. Sie müssen also auch gleich schnell gealtert sein.
Einen anderen Eindruck hatten sie nur, solange sie sich aus verschiedenen Bezugssystemen heraus betrachtet haben (nur ihre S i c h t e n waren verschieden).
Gruß,
grtgrt
Okotombrok in 1997-99:Grtgrt in 1997-94:
Das Szenario symmetrisch zu machen erlaubt uns zu erkennen, dass — in der SRT —
die beobachtete Zeitdilation nur in den S i c h t e n der beiden Beobachter auftritt, aber eben n i c h t in der Raumzeit selbst.
Dummes Zeug,
das einzige, was dein Szenario erkennen lässt ist, dass unter gleichen Bedingungen Bedingungen herrschen, die zu gleichen Bedingungen führen.
Das wusste ich aber auch schon vorher.
Okotombrok:
Du denkst einfach nicht weit genug.
Wenn im Beispiel aus Beitrag 1997-80 eine der beiden Personen X und Y — wir dürfen annehmen, es sei X — t a t s ä c h l i c h weniger schnell altern würde als der andere, müsste X — wenn sie sich wieder treffen — jünger sein als Y.
Nach der SRT aber unterscheiden sich die Sichten beider auf den jeweils anderen aber überhaupt nicht. Und deswegen muss, was für X richtig ist, auch für Y richtig sein.
Demzufolge gilt, wenn sie sich wieder treffen,
Das aber kann nur sein, wenn beide nun gleiches Alter haben. Sie müssen also auch gleich schnell gealtert sein.
Einen anderen Eindruck hatten sie nur, solange sie sich aus verschiedenen Bezugssystemen heraus betrachtet haben (nur ihre S i c h t e n waren verschieden).
Gruß,
grtgrt
Beitrag 1997-91
-
Hi Okotombrok:
Es ist ein F a k t u m (also keine T h e s e ), dass das Zwillingsparadoxon in der SRT nicht lösbar ist: Es tritt dort nämlich gar nicht erst auf (!) .
Begründung:
Wir betrachten wieder die beiden Objekte (Raumfahrer etwa), die sich zunächst mit konstanter Geschwindigkeit voneinander entfernen (Phase 1) um dann — wenn beide glauben, dass sie jetzt z.B. genau 10000 km weit voneinander entfernt sind — spontan umzukehren und mit gleicher Geschwindigkeit wieder auf den jeweils anderen zuzurasen (Phase 2).
Natürlich geht das nicht, ohne abzubremsen und dann wieder zu beschleunigen. Das aber wird in der SRT nicht berücksichtigt, und deswegen gilt:
Mit anderen Worten: Was der eine in Phase 1 weniger schnell altert als der andere, altert er in Phase 2 schneller, und wenn beide sich wieder treffen ist die Summe dieser (nur scheinbar eingetretenen) Alterunterschiede wieder Null.
In der ART ist das ganz anders:
Dort wird die Tatsache, dass man zur Umkehr abbremsen und dann wieder beschleunigen muss, n i c h t einfach ignoriert. Beschleunigungskräfte aber sind von Gravitationskräften nicht unterscheidbar. Sie krümmen deswegen das "Gitter" der Raumzeit, und der Effekt ist, dass der Weg, den irgendein Objekt dieser Krümmung wegen nimmt, kürzer ist als der Weg, den es genommen hätte, wenn keine Krümmung des Raumes "Raumzeit" eingetreten wäre. Wenn nun aber zwei Personen verschiedene Wege durch die Raumzeit nehmen um sich dann wieder zu treffen, wird der weniger gealtert sein, der den kürzeren Weg genommen hat.
So also erklärt sich der Unterschied zwischen SRT und ART (und auch die Tatsache, dass Raum und Zeit als unterschiedliche Dimensionen der Raumzeit in der SRT noch ganz klar unabhängig voneinander wirken, während sie in der ART beim besten Willen n i c h t mehr als unabhängig von einander geformt zu verstehen sind.
PS: Die Tatsache übringens, dass die Minkowski-Metrik schon in der SRT räumliche und zeitliche Dimension zusammenführt (siehe 1997-55), bedeutet keineswegs, dass man beides — in der SRT wenigstens — nicht auseinander halten könne. Und in der Tat: Auch im 3-dimensionalen Raum, in dem jeder zu leben glaubt, der noch rein gar nichts von Relativitätstheorie gehört hat, sind ja klar unterscheidbar,
Beste Grüße,
grtgrt
Okotombrok in 1997-88:
Die These, das ZP sei nur mit der ART erklärbar, ist rein formal betrachtet falsch.
Hi Okotombrok:
Es ist ein F a k t u m (also keine T h e s e ), dass das Zwillingsparadoxon in der SRT nicht lösbar ist: Es tritt dort nämlich gar nicht erst auf (!) .
Begründung:
Wir betrachten wieder die beiden Objekte (Raumfahrer etwa), die sich zunächst mit konstanter Geschwindigkeit voneinander entfernen (Phase 1) um dann — wenn beide glauben, dass sie jetzt z.B. genau 10000 km weit voneinander entfernt sind — spontan umzukehren und mit gleicher Geschwindigkeit wieder auf den jeweils anderen zuzurasen (Phase 2).
Natürlich geht das nicht, ohne abzubremsen und dann wieder zu beschleunigen. Das aber wird in der SRT nicht berücksichtigt, und deswegen gilt:
- Während der Phase 1 sieht jeder den jeweils anderen l a n g s a m e r altern als sich selbst (und zwar deswegen, weil nach jedem Tick der Uhr des anderen, dieser andere weiter weg vom Beobachter ist, und das Signal, das vom anderen kommt, deswegen länger unterwegs sein wird.
- Während der Phase 2 aber sieht jeder den jeweils anderen s c h n e l l e r altern als sich selbst (da nämlich nach jedem Tick der Uhr des anderen die Entfernung zwischen dem Beobachter und dem Anderen kleiner wurde, und das Signal deswegen weniger lang unterwegs sein wird).
Mit anderen Worten: Was der eine in Phase 1 weniger schnell altert als der andere, altert er in Phase 2 schneller, und wenn beide sich wieder treffen ist die Summe dieser (nur scheinbar eingetretenen) Alterunterschiede wieder Null.
In der ART ist das ganz anders:
Dort wird die Tatsache, dass man zur Umkehr abbremsen und dann wieder beschleunigen muss, n i c h t einfach ignoriert. Beschleunigungskräfte aber sind von Gravitationskräften nicht unterscheidbar. Sie krümmen deswegen das "Gitter" der Raumzeit, und der Effekt ist, dass der Weg, den irgendein Objekt dieser Krümmung wegen nimmt, kürzer ist als der Weg, den es genommen hätte, wenn keine Krümmung des Raumes "Raumzeit" eingetreten wäre. Wenn nun aber zwei Personen verschiedene Wege durch die Raumzeit nehmen um sich dann wieder zu treffen, wird der weniger gealtert sein, der den kürzeren Weg genommen hat.
So also erklärt sich der Unterschied zwischen SRT und ART (und auch die Tatsache, dass Raum und Zeit als unterschiedliche Dimensionen der Raumzeit in der SRT noch ganz klar unabhängig voneinander wirken, während sie in der ART beim besten Willen n i c h t mehr als unabhängig von einander geformt zu verstehen sind.
PS: Die Tatsache übringens, dass die Minkowski-Metrik schon in der SRT räumliche und zeitliche Dimension zusammenführt (siehe 1997-55), bedeutet keineswegs, dass man beides — in der SRT wenigstens — nicht auseinander halten könne. Und in der Tat: Auch im 3-dimensionalen Raum, in dem jeder zu leben glaubt, der noch rein gar nichts von Relativitätstheorie gehört hat, sind ja klar unterscheidbar,
- das, was in der Ebene existiert
- von dem, was sich — wie ein Berggipfel etwa — über sie erhebt (hinein in eine Dimension, die die Ebene nicht kennt).
Beste Grüße,
grtgrt
Beitrag 1997-35
-
An Eugen & Harti:
Im letzten Abschnitt seiner Seite Das Zwillingsparadoxon sagt uns der Physiker Joachim Schulz unmissverständlich:
Es sind also tatsächlich die Beschleunigsphasen, die bewirken, dass die Brüder nach Rückkehr des Reisenden nicht mehr gleich alt sind.
Gruß,
grtgrt
Bauhof in 1997-34:
Und nebenbei bemerkt, erhellt aus dem Drillingsparadoxon auch, dass nicht die Beschleunigungsphasen für das unterschiedliche Altern verantwortlich sind.
An Eugen & Harti:
Im letzten Abschnitt seiner Seite Das Zwillingsparadoxon sagt uns der Physiker Joachim Schulz unmissverständlich:
Zitat:
Dass aus der Sicht des Reisenden die Erdzeit langsamer vergeht während für die Erdbevölkerung die Zeit des Reisenden langsamer vergeht, ist kein Widerspruch, wenn man die Verzerrung der Weltsicht während der Beschleunigungen berücksichtigt. Das ist die Relativität der Gleichzeitigkeit.
Der reisende Zwilling ist der, der die Beschleunigungen durchführt. Dadurch ist er stets weniger gealtert als sein zuhause gebliebener Zwilling.
Es sind also tatsächlich die Beschleunigsphasen, die bewirken, dass die Brüder nach Rückkehr des Reisenden nicht mehr gleich alt sind.
Gruß,
grtgrt
Beitrag 1997-53
-
Für die ART scheint mir das richtig, für die SRT aber nicht — sie diskutiert ja nur beobachterspezifische S i c h t e n (und nicht auch Wege, die teilweise oder gar ausschließlich durch die Zeit führen: In der SRT sind es immer Wege, die rein nur durch den Raum führen, für den Reisenden aber gewisse Zeit erfordern).
Raum und Zeit sind deswegen in der Argumentation sauber auseinander gehalten,
und nur deswegen kann sich die SRT leisten, als Bezugssystem keine 4-dim Mannigfaltigkeit, sondern nur einen 4-dim-Vektorraum zu haben.
Aber ich weiß: Ihr werdet mir da nicht zustimmen ....
Henry in 1997-51:
Raum und Zeit sind in der SRT sowie in der ART NICHT mehr voneinander zu trennen, das Konzept von Raum und Zeit getrennt zu betrachten ist mit den Relativitätstheorien aufgehoben. Punkt.
Objekte bewegen sich deshalb immer mit Lichtgeschwindigkeit, weil sie sich IMMER durch die Raumzeit bewegen, also durch Raum und Zeit als untrennbare Gesamtheit.
Für die ART scheint mir das richtig, für die SRT aber nicht — sie diskutiert ja nur beobachterspezifische S i c h t e n (und nicht auch Wege, die teilweise oder gar ausschließlich durch die Zeit führen: In der SRT sind es immer Wege, die rein nur durch den Raum führen, für den Reisenden aber gewisse Zeit erfordern).
Raum und Zeit sind deswegen in der Argumentation sauber auseinander gehalten,
und nur deswegen kann sich die SRT leisten, als Bezugssystem keine 4-dim Mannigfaltigkeit, sondern nur einen 4-dim-Vektorraum zu haben.
Aber ich weiß: Ihr werdet mir da nicht zustimmen ....
tags: SRT1gegreit Zwilling1gegreit ART1gegreit
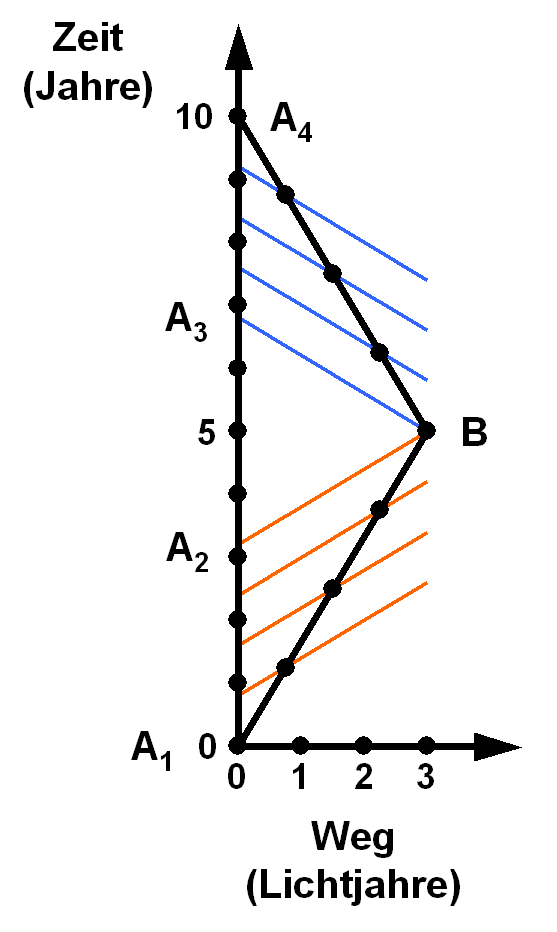
 Nach oben
Nach oben